Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.5. Раскраска графов и вопросы топологии

Планарные графы на торе

Если мы соединим все четыре столицы государств 1, 2, 3 и 4 (рис. 3.67) сплошными линиями, то получим проекцию тетраэдра на плоскости. Добавление еще одной вершины графа дорог превращает планарный граф тетраэдра в непланарный граф с пятью вершинами, ребра которого уже нельзя уложить на плоскости без пересечений. Оказывается, максимальное число вершин планарного графа, который может быть вычерчен на некоторой поверхности, однозначно характеризует топологические свойства последней. Топологические свойства плоскости и топологические свойства сферы одинаковы, так как все точки сферы S (рис. 3.69) можно спроецировать из полярной точки N на все точки плоскости P путем последовательного винтового скольжения проекционной прямой. Последовательность точек получающейся при этом скольжении спирали на сфере и спирали на плоскости нигде не будет нарушена. Значит, тетраэдр будет однозначно характеризовать и топологию сферической поверхности.

Рис. 3.69

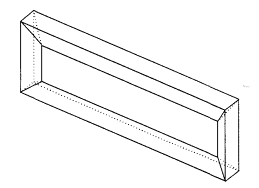
Топологические свойства рамы, образованной трехгранными призмами (рис. 3.70), эквивалентны топологическим свойствам тора. Если в качестве образующих рамы взять 4-гранные, 5-гранные, …, n-гранные призмы, то все они будут обладать топологическими свойствами тора. Представьте себе, что эти полые тела начали накачивать воздухом, подобно тому, как накачивают велосипедную камеру. Тогда все грани и вершины рам разгладятся, и в результате получится бублик, имеющий одну-единственную поверхность.

Рис. 3.70

Зададимся вопросом, каков порядок вершин полного графа, который можно было бы вычертить на поверхности тора так, чтобы его ребра нигде не пересекались? На гранях фигуры, изображенной на рис. 3.70, графы вычерчивать неудобно. Возьмем в качестве тора прямоугольную рамку, причем плоскую, только будем различать у нее внешнюю и оборотную плоскости. В поисках ответа на поставленный вопрос мы без труда вычертим на нашей рамке-торе граф-тетраэдр. После некоторых усилий нам удастся уложить без пересечения ребер и граф с пятью вершинами. Затратив немалые старания, мы, наконец, сумеем вычертить на прямоугольной раме планарный граф для тора с шестью вершинами; он изображен на рис. 3.71. Являются ли шесть вершин пределом для тора?

Рис. 3.71

Долгое время считалось, что полный граф с шестью вершинами является максимально возможным. Однако после разреза тора и вычерчивания его развертки в виде прямоугольника (рис. 3.72а), стало ясно, что шесть точек — это не предел. На рис. 3.72б удалось вычертить семь вершин полного графа, который сохраняет свойства планарности на всех тороидальных поверхностях, включая поверхности призматических рам, наподобие той, что вычерчена на рис. 3.70.

Рис. 3.72

Обратите внимание, что графы-карты, показанные на рис. 3.72 пунктирными линиями, получились регулярными: степень их вершин равна трем. Сколькими красками можно обойтись при раскраске политической карты с протяженными границами?

Ответ будет таким: семь цветов. Максимально планарный граф для данной топологической поверхности определяет и его хроматическое число. А как определить, какой граф для данной поверхности будет максимально планарным? Может быть, мы плохо искали, и на развертке тора поместятся не шесть или семь точек, как это показано на рис. 3.72, а восемь или девять? Где гарантия того, что наши эмпирические поиски вышли на действительно максимальное число вершин? Чтобы ответить на эти вопросы, мы должны еще раз вернуться к формуле Эйлера и ввести важное для топологии понятие связанности поверхности.