Sceptic-Ratio. ДМ 4-13. Субаттракторы

В этом подразделе мы уделим чуть большее внимание сложной иерархии аттракторов, образующих фрактальные структуры, уходящие в бесконечно малые пространства. Предыдущий анализ касался диапазона коэффициентов 0 < a < 3 тригонометрической рекурсивной функции ax cos(x). Теперь рассмотрим, как в аттракторах появляются субаттракторы при коэффициенте а = 3 и выше. Рис. 4.80 демонстрирует, что при а = 3 ничего особенного не происходит, т.е. нет каких-то признаков, которые бы свидетельствовали о существовании особых состояний мод вроде π-аттракторов при коэффициенте а = 1 или квазиаттракторов при а = 2. Большой аттрактор при этом значении коэффициента не разделен на аттрактор-плюс и аттрактор-минус, но в нем просматриваются широкие окна, сигнализирующие о том, что мы находимся в зоне формирования какого-то большого субаттрактора. Грубо изменяя значение коэффициента, мы убеждаемся, что при а = 3,12 для мод f 1 — f 6 существует субаттрактор четвертого рода, четыре уровня которого, однако, легко прокалываются уже десятой модой. Отсюда мы делаем вывод, что аттрактор 4-го рода на базе Большого аттрактора возникает где-то в пределах коэффициента 3 < a < 3,12. При поиске новых аттракторов всегда удобно сначала ориентироваться на младшие моды и грубые значения коэффициента а, потом переходить к старшим модам и более прецизионным значениям а.

Действительно, при а = 3,1 существует комбинированный аттрактор четвертого рода, который во многом напоминает комбинированный аттрактор четвертого рода, показанный на рис. 4.55. Оба аттрактора имеют идентичную фрактальную структуру, которая бесконечно воспроизводится в малых масштабах. На рис. 4.81 показаны пять первых мод, образующих четыре уровня комбинированного аттрактора. Ширина Большого аттрактора определяется крайними узлами сечения f 0/f 1. Нижний и верхний уровни сформированы сечениями f 1/f 5 и f 3/f 7 (мода f 7 не показана), а два средних уровня — сечениями f 0/f 2 и f 0/f 4. В левом нижнем углу этого же рисунка имеется окошко, где приведен график четырех мод f 501 — f 504 в миллиард раз увеличенном масштабе. Здесь мы можем видеть широкие и узкие просветы прямоугольной формы с теми же аттракторными уровнями. Для комбинированного аттрактора, изображенного на рис. 4.55, масштабный коэффициент был равен k = 3,7351. Но поскольку комбинированный аттрактор, изображенный на рис. 4.81, расположен симметрично относительно начала координат, выполняется равенство: k = а. Это означает, что состояние мод f 17 — f 21 ничем не будет отличаться от состояния мод f 1 — f 5, если масштаб изображения по оси абсцисс увеличить в а₁₆ = (3,1)¹⁶, т.е. примерно в 73 млн. раз.

В окошке рис. 4.81 можно видеть, что аттракторные уровни имеют ступенчатую форму. Для средних уровней эти ступеньки видны, что называется, невооруженным глазом. Чтобы рассмотреть эти ступеньки для нижнего и верхнего уровней, нужно произвести увеличение изображения в несколько сотен раз. Наличие ступенек свидетельствует о том, что при а = 3,1 произошла бифуркация одиночных уровней, которые видны в просветах, в результате чего возникла система дуплетов. Расщепление одиночного уровня на два подуровня произошло при коэффициенте а₁ = 3,08744. Следующая бифуркация, т.е. расщепление каждого из двух подуровней еще на два подуровня, произойдет при а₂ = 3,102308 (индекс при букве а совпадает с показателем степени бифуркации, т.е. степени числа 2), в результате чего появится мультиплет из четырех подуровней. Список коэффициентов бифуркации a_i и последовательность F_i приведены на рис. 4.82. Тема нахождения коэффициентов бифуркации и постоянной Фейгенбаума важна, поэтому ей желательно посвятить специальное практическое занятие. Числовое значение этой константы можно искать в любой области оси абсцисс, где построен аттрактор и для любого диапазона коэффициента а, если а > 1.

Последовательная цепь бифуркаций приводит к расщеплению первоначально одиночного уровня нашего комбинированного аттрактора четвертого рода на 512 подуровней. Таким образом, в просветах исходного аттрактора возникает «Крепостная стена» (фрагмент этой «стены» показан на рис. 4.82). Для всякой «Крепостной стены» можно вводить величину дробной размерности, которая, однако, не выражается каким-то одним дробным числом. Если измерять ширину оснований «башенок», которые вырастают на «Крепостной стене» в процессе бифуркации аттракторов, то окажется, что отношения оснований заметно отличаются друг от друга для различных «башенок». Таким образом, дробная размерность «Крепостной стены» колеблется в довольно широких пределах, по крайней мере, от 3 до 2. Выше уже говорилось о недостатках понятия фрактальной размерности, поэтому далее мы не станем касаться этой проблемы.

При плавном изменении коэффициента а, очередной коэффициент бифуркации a_i фиксируется при пересечении модой f 0 максимума f 2, f 4, ..., f 512. На рис. 4.82 показан момент прохождения диагонали f 0 на максимум моды f 512. Точность нахождения коэффициент a_i ничем не ограничена, разве что шумовой составляющей, которая в области аттрактора имеет самое низкое значение и дает о себе знать на пределе вычислительных возможностей компьютера. Для 16-разрядного процессора ее влияние сказывается примерно на 14 знаке после запятой (о шуме и хаосе поговорим подробно чуть позже). Аттракторы могут находиться на любом участке оси абсцисс, в том числе, и вдали от диагонали f 0. Между тем, как было сказано, «Крепостная стена» возникает на любом аттракторе и для каждого из них будет иметь место индивидуальный ряд коэффициентов бифуркации. Как быть в этом случае?

Очень просто: вести настройку моды f 1 на максимумы мод f 3, f 5 ... f 513. Если под рукой не оказалось моды f 1, берите моду f 2 и ориентируйтесь на максимумы мод f 4, f 6, ..., f 514 и т.д. Главное, чтобы разность между секущей и пересекающейся модами давало ряд чисел: 2, 4, ..., 512. На рис. 4.83 можно видеть, что моменты пересечения максимумов мод f 4, f 5 и f 7, соответственно, с секущими модами f 0, f 1 и f 3 в точности совпадают, т.е. происходят при одном и том же коэффициенте бифуркации а₂ = 2,41881016. Этой согласованностью мод и нужно воспользоваться, когда через аттракторный уровень не проходит прямая f 0.

Обратившись к рис. 4.83, мы отошли от комбинированного аттрактора 4-ого рода, возникшего при а > 3, и стали рассматривать бифуркации Большого аттрактора, что весьма кстати. Дело в том, что это не только самый заметный аттрактор из всех существующих для тригонометрической функции, он еще дает и наиболее точное значение для постоянной Фейгенбаума. Ранее выстроенная «Крепостная стена» находилась на одном из четырех уровней аттрактора четвертого рода. Мы начинали с коэффициента а₁ = 3,08744, сразу ориентируясь на максимум моды f 2 и не принимая во внимание появление единичной линии, которая возникает от сечения мод f 0/f 1. Таким образом, забравшись в диапазон коэффициентов а > 3, мы миновали основную область коэффициентов, которую имеют в виду, когда строят традиционную бифуркационную диаграмму. Сейчас мы заполнили этот пробел соответствующим списком бифуркационных коэффициентов, который приведен на рис. 4.83.

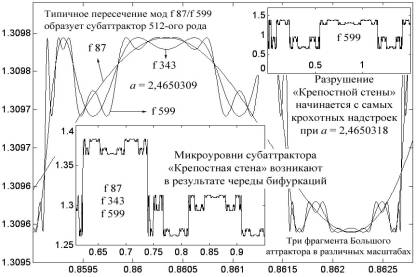
На рис. 4.84 даны три фрагмента Большого аттрактора, когда на нем возвышается «Крепостная стена», выстроенная десятью модами с f 1 по f 512. Самым крупным планом дается детальное изображение мод f 87, f 343 и f 599. Оно позволяет понять, почему «Крепостная стена» сплошь представлена аттракторными уровнями, т.е. некой ломаной линией, которая нигде не прерывается на свободное колебание мод, которое существует вне аттракторов. Дело в том, что аттрактор, как известно, определяется точками притяжения, в качестве которых здесь выступают узлы сплетения указанных мод. Если мысленно провести все линии между этими узлами, то мы как раз и получим ту самую ломаную, которая образует контуры «Крепостной стены». В этом смысле дуплетные уровни качественно отличаются от триплетных и других мультиплетных уровней. Триплеты и мультиплеты появляются в отдельных окнах на фоне свободного колебания мод, где могут интенсивно развиваться шумовые процессы; дуплеты же целиком покрывают пространство оси абсцисс аттракторными уровнями, не давая развиваться шумам.

Почему выбрана мода f 87? Только потому, чтобы показать, что для определения бифуркационных коэффициентов и строительства стены, годятся любые моды. Последующий отбор мод — f 343 и f 599 — продиктован 256 и 512 порядками, которыми те отличаются от моды f 87. Мода f 87 не проходит через экстремумы моды f 599, а это значит, что состояние мод, изображенное на рис. 4.84, не отвечает моменту девятой бифуркации. Действительно, коэффициент а = 2,4650309, при котором изображен график, несколько выше коэффициента бифуркации а₉ = 2,4650303137. Стоит коэффициенту измениться еще на одну миллионную долю, как начинается процесс разрушения «Крепостной стены». При а = 2,4650318 и выше происходят проколы микроуровней самых высоких мультиплетов, т.е. указанное значение коэффициента является предельно допустимым для процесса бифуркации (его мы ранее обозначали символом a_∞). На проколотых бифуркационных уровнях возникают микроуровни нечетных субаттракторов, о чем мы подробно поговорим ниже. Но уже сейчас нужно отчетливо понимать, что шумовые процессы не начнутся до тех пор, пока не исчезнет фундамент «Крепостной стены», т.е. основной уровень Большого аттрактора.

Процесс прокола бифуркационного уровня происходит обычным образом по известной нам схеме. Выход высших мод за границы, очерченные низшими модами, показан на рис. 4.85, только в качестве базового здесь выбран уже не Большой аттрактор, а 2π-аттрактор, где, разумеется, имеют место те же самые бифуркационные процессы, что и на Большом аттракторе. Рис. 4.86, как и предыдущий рисунок, иллюстрирует прокол субаттрактора 32-го рода, который возник в центральной части аттрактора, изображенного на рис. 4.55. Через вершину «башни» комбинированного аттрактора, возвышающейся над «Крепостной стеной», проходит положительная диагональ f 0, которая пронизывает и все высшие моды субаттрактора 32-го рода. Прокол осуществлен модами f 64, f 96, f 128, f 160 и f 192, которые образовали точно такую же конфигурацию, как моды f 2, f 3, f 4, f 5 и f 6 в момент прокола Большого аттрактора первого рода (рис. 4.59), или как моды f 3, f 5, f 7, f 9 и f 11 в момент прокола аттрактора второго рода (рис. 4.61). Моды, участвующие в проколе аттракторного уровня или субаттракторного микроуровня, всегда принадлежат к одному классу; по ним можно легко определить и род аттрактора или субаттрактора.

С а = 3,0 по а = 2,54 происходит непрерывная и однотипная перестройка всех мод Большого аттрактора, однако в определенный момент, а именно, при а = 2,65, почти мгновенно, с точки зрения равномерного хода изменения коэффициента а, образуется множество окон и начинают формироваться три микроуровня субаттрактора 3-его рода. Данная фаза изменения Большого аттрактора является важной; о ней постоянно пишется в книгах по динамическим процессам. Об этой фазе говорили и мы, когда рассказывали о бифуркационной диаграмме. Для функции f (z) = z² + c, где c = a + ib, трехуровневая система появляется при a = –1,7549. Для функции ax (1 – x) три уровня появляются при a = 3,8264. Трехуровневый субаттрактор для тригонометрической функции ax cos (x) держится в широком диапазоне изменения коэффициента a (2,64 ÷ 2,66), если его сопоставлять с приведенными выше значениями, хотя, с точки зрения общего изменения коэффициента a (3,0 ÷ 2,0), эту фазу можно легко упустить из виду.

На рис. 4.87 приведены пять графиков, соответствующих пяти иерархическим ступеням сложного субаттрактора 486-го рода. В левом верхнем углу изображен Большой аттрактор во всю ширину в фазе 3-аттрактора. Центральный уровень этого 3-аттрактора, на который указывает большая стрелка, справа вверху представлен в увеличенном виде. Второй график, как и первый, образован модой f 489, но на нем видна парабола от моды f 3. Левая ветвь этой параболы пересекает средний аттракторный уровень, который на третьем графике дан в увеличенном масштабе. У 3-аттрактора уровни представлены дуплетом, причем каждая его пара уровней расщеплена еще на три подуровня, которые можно видеть на четвертом графике. Наконец, последнее сечение f 3/f 489, которое дает еще три уровня, показано на пятом фрагменте. В итоге возник сложный шестизвенный мультиплет, в состав которого включены пять триплетов и один дуплет.

Мультиплет, изображенный на рис. 4.88, состоит из четырех дуплетов и одного триплета. Как и в предыдущем случае, здесь важна последовательность образования аттракторных уровней. Данный мультиплет, возникший при a = 2,44204426, образован на базе аттрактора второго рода, который дал первый дуплет. В конце иерархии находится триплет, уровни которого кратны 16. Если иметь в виду самое широкое окно центральной части аттрактора второго рода, расположенное на уровне 8,0296 при x = 2,24552, то самый нижний микроуровень этого окна сформирован модами f 16, f 64, f 112 и f 160; средний уровень — модами f 48, f 96 и f 144, а верхний — модами f 32, f 80 и f 128 (разобраться в раскладе мод поможет фрагмент, составленный из мод f 16, f 32, f 48 и f 64, расположенный выше обсуждаемой области с просветами).

Таким образом, участвующие в формировании этих микроуровней моды, кратные числу 16, чередуются через две на третью, т.е. данные микроуровни принадлежат субаттрактору 48-го рода. Хотя в средних микроуровнях по всей длине аттрактора второго рода участвуют четные моды порядка:

они являются нечетными модами относительно числа 16.

Одним из основных заданий лабораторно-практического занятия по теме «Аттракторы» должно стать построение аттрактора по величине его рода при заданной определенной цепочке множителей. Например, требуется построить аттрактор 480-го рода, когда чередование его субаттракторов удовлетворяет следующей цепочке множителей: 2 · 5 · 3 · 2 · 2 · 4. При этом выбор мод может быть конкретизирован преподавателем или самим студентом. Отчет представляется в форме серии графиков, отображающих отдельные субаттракторы, как это показано на рис. 4.89. Очевидно, что другой последовательности множителей (не обязательно простых) будет отвечать совершенно иная аттракторная система уровней и соответствующий ей коэффициент а. Так, два ряда множителей: 4 · 3 · 2 · 5 · 2 · 2 и 5 · 2 · 4 · 2 · 2 · 3, дают совершенно новые коэффициенты и аттракторные уровни, отличающиеся как друг от друга, так и от предыдущего случая.

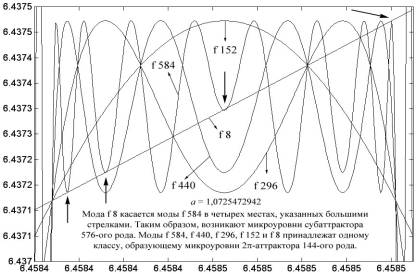
Можно сформулировать лабораторно-практическое задание попроще. Например, получить изображения мод, принадлежащих одному классу — f 8, f 152, f 296, f 440, f 584, с тем чтобы в зоне 2π-аттрактора построить сечения для уровней 432-го (рис. 4.90) или 576-го рода (рис. 4.91). В общем, здесь имеется обширное поле деятельности для составления самых разнообразных лабораторно-практических упражнений для тех, кто изучает аттракторы от рекурсивных функций типа ax cos(x), ax exp(1 – x), ax (1 – x) и т.д.

Нам остается ответить на последний вопрос: сколько видов аттракторов рода 3, 4, 5, 6 и т.д. существует и есть ли здесь какая-нибудь закономерность?

Ранее мы выяснили, что при каком-то значении коэффициента а аттрактор возникает в виде основного аттракторного уровня. При увеличении коэффициента а начинается процесс бифуркации этого уровня и строительство «Крепостной стены». По достижении коэффициентом a значения a_∞ «стена» начинает разрушаться, причем с самых верхних этажей. Здесь появляются субаттракторные микроуровни 3, 4, 5, 6-го и т.д. родов. При появлении 3-аттрактора три его уровня могут испытать всю бесконечную цепь бифуркаций, затем цепь проколов и образование новых субаттракторов 3, 4, 5, 6-го и т.д. родов. При появлении 4-аттрактора четыре его уровня также могут испытать бифуркацию, проколы и образование совершенно других субаттракторов 3, 4, 5, 6 и т.д. родов. В этом проявляется фрактальная природа аттракторов.

На рис. 4.92 изображен фрагмент «Крепостной стены», выстроенной на комбинированном аттракторе 4-го рода, когда аттрактор имеет 64 устойчивых уровня, верхний уровень «стены», однако, почти разрушен, т.е. мода f 128 уже не образует соответствующих ей уровней. Это состояние отвечает коэффициенту а = 3,1081236. При небольшом росте данного коэффициента (а = 3,108123905) мода f 576 образует 9-аттрактор. Дальнейшее увеличение коэффициента приводит к появлению аттракторов 7, 5 и 3-го родов. Аналогичная картина наблюдается на всех этажах «Крепостной стены».

Например, рис. 4.93 демонстрирует нечетные аттракторы, появляющиеся на основном уровне аттрактора 4-го рода. 3-аттрактор всегда имеет одну модификацию (поз. 1); 5-аттрактор — три модификации (поз. 2 — 4 и поз. 5 — 7); 7-аттрактор — девять модификаций, которые возникают при следующих коэффициентах:

(одна из этих модификаций представлена поз. 8). Число модификаций 9-аттрактора равно 27 и еще одна модификация, образованная 3-аттрактором, когда в нем появляется триплет от 3-субаттрактора, т.е. когда появляется 3·3-аттрактор. Если не учитывать эти комбинированные модификации, то количество видов нечетных аттракторов подчиняется элементарной закономерности: 3⁰, 3¹, 3², 3³, ... В частности, можно ожидать, что число модификаций аттракторов 15-го рода равно 735, так как 3⁶ = 729 и еще шесть комбинаций дают аттракторы рода 3 · 5 и 5 · 3. На рис. 4.93 поз. 9 — 12 показано по одному нечетному аттрактору 9, 11, 13 и 15-го родов. Таким образом, число модификаций аттракторов нечетного рода поддается простому подсчету, особенно тогда, когда его род выражается простым числом. Например, число 101 — простое, следовательно, количество модификаций 101-аттрактора равно только 49 степени числа 3.

Аналогичная картина наблюдается для рекурсивных функций, отличных от тригонометрической ax cos(x). В частности, для экспоненциального закона ax exp(1 – x) нечетные аттракторы возникают при следующих коэффициентах:

Последний из этого ряда аттракторов представлен на рис. 4.94. Количество модификаций нечетных аттракторов подчиняется той же последовательности степеней числа 3. Так, например, два других 5-аттрактора возникают приблизительно при коэффициентах a = 10,6 и a = 18,7. Оставшиеся восемь 7-аттракторов существуют при коэффициентах a = {7,3; 9,9; 11,2; 12,3; 14,9; 16,9; 21,5; 29,6} и т.д.

Указанная закономерность распространяется на классический закон Ферхюльста ax(1 – x), который является наиболее простым. В табл. 4.9 приведены коэффициенты a для всех нечетных аттракторов этой квадратичной зависимости. К указанной таблице нужно сделать примечание: значение коэффициента а, который помечен значком 1, принадлежит 3 · 3-аттрактору; нечетные аттракторы выше 9-го рода представлены самым первым коэффициентом с указанием общего числа модификаций. Поиск коэффициентов велся по известной методике, т.е. по самому чувствительному максимуму, расположенному в точке x = 0,5. Коэффициент фиксировался на момент совпадения экстремума 0,5 с диагональю f 0. Для функции ax exp(1 – x) такой точкой является x = 1,0; для тригонометрической функции ax cos(x) ей соответствует точка x = 0,86033359. В количествах модификаций четных аттракторов не удается обнаружить какой-либо закономерности.

Таблица 4.9

3-аттрактор	9-аттрактор	3,975920	13-аттрактор
3,831874055283316	3,687221	3,979542	3,679704; ...
5-аттрактор	3,717118	3,983141	Колич.: 243
3,738914912970685	3,761262	3,986275	15-аттрактор
3,905706469831291	3,785779	3,989188	3,678977; ...
3,990267046973701	3,853727₁	3,991325	Колич.: 735
7-аттрактор	3,879418	3,993579	17-аттрактор
3,701769153537955	3,892266	3,995418	3,678718; ...
3,774214188900913	3,917796	3,996945	Колич.: 2187
3,922193403309700	3,926282	3,998148	19-аттрактор
3,922193403309700	3,934704	3,999058	3,678624; ...
3,951032164761305	3,940372	3,999661	Колич.: 6561
3,968976856955538	3,947738	3,999963	...
3,984747618815538	3,954486	11-аттрактор	101-аттрактор
3,994537809111197	3,966194	3,681711; ...	3,678574; ...
3,999397060962097	3,971415	Колич.: 81	Колич.: 3 ^ 49

Полный список коэффициентов а аттракторов 2, 4, 6, 8 и 10-го родов, расписанных по всем видам (номер вида указан нижним индексом), включая бифуркационные коэффициенты, для закона ax(1 – x) приведен в табл. 4.10.

Таблица 4.10

Род _Вид	a	Род _Вид	a	Род _Вид	a
2	3,236068	2 · 5₂	3,647049	10₂₂	3,974813
2 · 2	3,498562	2 · 5₃	3,673008	10₂₃	3,977128
4	3,960269	5 · 2₁	3,741848	10₂₄	3,978418
2 · 3	3,627558	10₁	3,794066	10₂₅	3,980509
3 · 2	3,844568	10₂	3,808498	10₂₆	3,982279
6₁	3,937536	10₃	3,865265	10₂₇	3,983985
6₂	3,977766	10₄	3,874923	10₂₈	3,985494
6₃	3,997583	10₅	3,884101	10₂₉	3,987023
2 · 2 · 2	3,554641	10₆	3,888016	10₃₀	3,988457
2 · 4	3,662194	10₇	3,895947	5 · 2₃	3,990306
8₁	3,800771	5 · 2₂	3,906241	10₃₁	3,991950
8₂	3,870541	10₈	3,915006	10₃₂	3,993059
8₃	3,899469	10₉	3,920553	10₃₃	3,994075
8₄	3,912046	10₁₀	3,923814	10₃₄	3,994982
8₅	3,930473	10₁₁	3,928482	10₃₅	3,995829
8₆	3,944214	10₁₂	3,932461	10₃₆	3,996591
4 · 2	3,960934	10₁₃	3,942435	10₃₇	3,997282
8₇	3,973724	10₁₄	3,945937	10₃₈	3,997869
8₈	3,981409	10₁₅	3,949599	10₃₉	3,998405
8₉	3,987746	10₁₆	3,952504	10₄₀	3,998859
8₁₀	3,992519	10₁₇	3,956613	10₄₁	3,999237
8₁₁	3,996220	10₁₈	3,964371	10₄₂	3,999538
8₁₂	3,998642	10₁₉	3,967760	10₄₃	3,999765
8₁₃	3,999850	10₂₀	3,970134	10₄₄	3,999915
2 · 5₁	3,605386	10₂₁	3,972607	10₄₅	3,999990

Дискретная математика:
логика, группы, графы, фракталы

4.13. Субаттракторы

Таблица 4.9

Таблица 4.10

Дискретная математика: логика, группы, графы, фракталы

4.13. Субаттракторы

Таблица 4.9

Таблица 4.10

Дискретная математика:
логика, группы, графы, фракталы