Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
4.14. Хаос
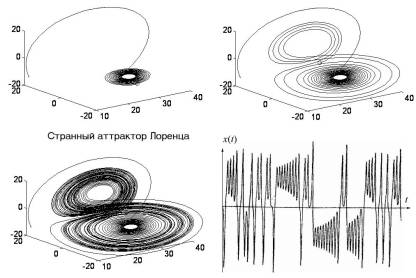
Ранее постоянно подчеркивалась фрактальная природа высших мод относительно низших: высшие моды могут быть сильно сжаты по оси абсцисс, но во всем остальном они остаются подобными низшим. В левом верхнем углу рис. 4.95 изображена мода f 64 функции ax cos(x) вблизи границы Большого аттрактора, которой соответствует значению x = 1,99273648664511. Вычислительная система MATLAB v. 4.0, работающая с 16-разрядным процессором, не позволяет подойти ближе к указанной границе, хотя сама мода f 64 имеет аналогичную конфигурацию при гораздо меньших масштабах по оси абсцисс. Для сравнения в правом верхнем углу рис. 4.95 показан график моды f 20, которая принадлежит тому же классу и развернута в тех же пределах, что и мода f 64. Мода меньшего порядка, но того же класса уже «перешагнет» указанную всего до 14-го знака после запятой границу Большого аттрактора. Кстати сказать, чтобы различать конфигурации микроуровней отдельных классов, можно ввести наборы из нулей и единиц. Например, мода f 54 будет принадлежать классу 011, потому что указанными тремя символами можно закодировать микроуровни субаттрактора 8-го рода в точке x = 0,2 (указано стрелками на левом нижнем рисунке). Мода f 61 принадлежит классу 100 субаттрактора 8-го рода, а у моды f 5 можно различать микроуровни только для субаттрактора 4-го рода; более мелких уровней «Крепостной стены» у нее просто не существует.
Рис. 4.95
Далее поставим вопрос: что произойдет с амплитудой мод вблизи границы Большого аттрактора, если зафиксировать величину коэффициента (пусть он будет равен a = 2,44161826171) и значение переменной x? Ответ на этот вопрос во многом зависит от того, насколько точно удалось определиться с координатой x; вблизи границы аттрактора амплитуда мод может принимать диаметрально противоположные значения. Рис. 4.96 демонстрирует выход амплитуды высших мод на аттрактор-плюс и аттрактор-минус, когда значение переменной x отличается на 0,00000000000001 (по оси x всех четырех графиков этого рисунка откладывается порядок моды). Как было указано выше, граница Большого аттрактора проходит в точке x = 1,99273648664511; при x = 1,99273648664510 мода f 20 и все последующие выходят на микроуровни аттрактора-минус, а уже при x = 1,99273648664509 эти моды попадают на микроуровни аттрактора-плюс. Однако величина 1,0e–14 не является пределом точности для высших мод. На самом деле конфигурации с положительными и отрицательными микроуровнями, показанные на рис. 4.95, спрессованы еще более плотно, так что, выбирая значение переменной непосредственно около границы аттрактора, амплитуда моды практически случайно принимает значения либо положительные, либо отрицательные. Обе указанные точки находятся левее границы Большого аттрактора, которая в действительности указана достаточно приблизительно. Если взять x = 1,99273648664512, то все моды после f 20 быстро уходят на бесконечно большие значения (левый нижний график), так как силы притяжения аттрактора «Крепостная стена» в этой точке прекращают свое действие. Но стоит нам отступить по оси x чуть правее, как показано на правом нижнем графике рис. 4.96, и амплитуда высших мод неожиданно попадает на отрицательные микроуровни нового аттрактора, который сформировался вблизи Большого аттрактора и о существовании которого мы не подозревали.
Рис. 4.96
Так возникает иллюзия «хаотического» перепрыгивания мод с отрицательных значений на положительные, и наоборот, при ничтожном изменении переменной x в ту или иную сторону. То, что вполне понятно при больших масштабах, становится непредсказуемым, когда мы попадаем в пространство очень малых измерений (малых, по крайней мере, для данной вычислительной системы и разрядности процессора). В табл. 4.11 приведены координаты границы перехода с уровней аттрактора-плюс на уровни аттрактора-минус (+/–), и наоборот (–/+), при коэффициенте а = 2,44181626171, соответствующему рис. 4.95 и рис. 4.96. Чем ближе к правой границе Большого аттрактора, которому отвечает предельная координата x∞ = 1,99273648664511, где существует полная неопределенность в отношении знака аттракторных уровней, тем чаще происходит смена границ между аттрактором-плюс и аттрактором-минус. Если из этих значений координат xi составить разности и найти отношения, то получится ряд Fi , сходящийся к некоторой константе F∞ , близкой к числу 5,43914. На самой же границе Большого аттрактора x∞ для нас, работающих с модами выше 20-го порядка, будет господствовать полный «хаос», хотя все поддается измерению, если моды имеют порядок, меньше 20-го.
Таблица 4.11
| Переход | Координаты границ | Fn = (xn + 1 – xn)/(xn – x n – 1) |
| +/– | x0 = 1,57079632679490 | F0 = 4,58174278990027 |
| –/+ | x1 = 1,91363449969659 | F1 = 5,31449907796902 |
| +/– | x2 = 1,97814446909764 | F2 = 5,41754555847309 |
| –/+ | x3 = 1,99005206981918 | F3 = 5,43521435225594 |
| +/– | x4 = 1,99224289431106 | F4 = 5,43841841617014 |
| –/+ | x5 = 1,99264573652073 | F5 = 5,43900598258604 |
| +/– | x6 = 1,99271980193102 | F6 = 5,43911396220626 |
| –/+ | x7 = 1,99273341911404 | F7 = 5,43913379924745 |
| +/– | x8 = 1,99273592267132 | F8 = 5,43913753046993 |
| –/+ | x9 = 1,99273638295703 | F9 = 5,43913755265008 |
| +/– | x10 = 1,99273646758179 | F10 = 5,43913832227238 |
| ... | ... | ... |
| ±/0 | x∞ = 1,99273648664511 | F∞ ≈ 5,43914 |
Рис. 4.97
Такое же «беспорядочное» перепрыгивание рекурсивной функции с одной орбиты на другую наблюдается на аттракторе Лоренца, изображенном на рис. 4.97. Здесь «хаотичность» усугубляется еще и тем, что конфигурация границ аттрактора Лоренца, его, так сказать, тонкая структура скрыта от наших глаз, поэтому все выглядит по меньшей мере «странно». Сначала вращение переднего фронта графического изображения функции происходит в одной плоскости, потом орбита этой пространственной функции неожиданно перепрыгивает в другую плоскость, сделав несколько оборотов, траектория снова переходит на первоначальную плоскость, и эти непрекращающиеся скачки воспринимаются как абсолютно случайные, но, конечно, они по своей сути таковыми не являются.
«Странный» аттрактор изучается с 1963 г., когда он был открыт Лоренцем при моделировании неравномерно прогреваемого атмосферного воздуха. Разогрев воздуха со стороны Земли и охлаждение его с противоположной приводит к конвекционным потокам, которые приближенно описываются системой трех дифференциальных уравнений, не имеющих точного аналитического решения: dx/dt = s(y – x), dy/dt = x(r – z) – y, dz/dt = xy – bz, где s = 10, r = 28, b =8/3. При вычислении на компьютере функция x(t), изображенная на правом нижнем графике рис. 4.97, ведет себя точно так же, как орбиты мод, показанные на рис. 4.96. Если изменить начальные значения x(t0) на несколько ничтожных долей, то через некоторое время t – t0 функция x(t) уже не выйдет на прежние значения амплитуд, так как она попадет на совершенно иную систему аттракторных уровней и ее новые переходы будут совсем не похожи на предыдущие. Поскольку тонкая структура данного аттрактора сложна и имеет огромное количество микроуровней, то заранее предсказать значения функции x(t) в каждой точке горизонтальной оси практически невозможно. Странный аттрактор Лоренца, которым заинтересовались не только метеорологи, пытающиеся составлять долгосрочные прогнозы погоды, но и математики, занимающиеся динамическими процессами, подсказал основное условие для возникновения хаоса: хаос возникает там, где имеется существенная зависимость от начальных условий. Вот, как об этом написал Ричард Кроновер в известном учебнике «Фракталы и хаос»:
«Согласно описанию эксперимента, принадлежащему самому Лоренцу, он вычислял значения решения в течение длительного времени, а затем остановил счет. Его заинтересовала некоторая особенность решения, которая возникала где-то в середине интервала счета, и поэтому он повторил вычисления с этого момента. Результаты повторного счета, очевидно, совпали бы с результатами первоначального счета, если бы начальные значения для повторного счета в точности были равны полученным ранее значениям для этого момента времени. Лоренц слегка изменил эти значения, уменьшив число верных десятичных знаков. Ошибки, введенные таким образом, были крайне невелики. Но самое неожиданное было впереди. Вновь сосчитанное решение некоторое время хорошо согласовывалось со старым. Однако, по мере счета расхождение возрастало, и постепенно стало ясно, что новое решение вовсе не напоминает старое. Лоренц вновь повторял и проверял вычисления (вероятно, не доверяя компьютеру), прежде чем осознал важность эксперимента. То, что он наблюдал, теперь называется существенной зависимостью от начальных условий — основной чертой, присущей хаотической динамике. Существенную зависимость иногда называют эффектом бабочки. Такое название относится к невозможности делать долгосрочные прогнозы погоды. Сам Лоренц разъяснил это понятие в статье "Предсказуемость: может ли взмах крылышек бабочки в Бразилии привести к образованию торнадо в Техасе? ", опубликованной в 1979 году».
Будет, по-видимому, уместно привести слова из книги «Порядок в хаосе», авторы которой также касаются характеристики странных аттракторов. «Термин странный аттрактор, — пишут Берже, Помо и Видаль, — указывает на необычные свойства таких аттракторов, из которых наиболее важным является чувствительная зависимость от начальных условий (ЧЗНУ). Вследствие ЧЗНУ любые две первоначально близкие траектории на аттракторе в конце концов расходятся. Более того, расхождение траекторий (усредненное по коротким интервалам времени) возрастает со временем экспоненциально. … Обращение в нуль автокорреляционной функции, широкополосный спектр Фурье и внутренняя непредсказуемость системы — все это следствия ЧЗНУ. В частности, понятно, что малейшая ошибка или неточность в задании начального условия не позволяет нам решить, по какой траектории пойдет эволюция системы, и вынуждает ограничиться статистическим предсказанием долговременного будущего системы. Таким образом, мы приходим к результату, в высшей степени нетривиальному: выводу о непредсказуемости поведения некоторых детерминированных потоков всего лишь с тремя степенями свободы!..
Но само по себе понятие странного аттрактора не решает проблемы, поскольку немедленно возникает другой вопрос: как возникает странный аттрактор или, если угодно, как устанавливается хаотический режим? Какими маршрутами переходит динамическая система от регулярного режима к хаотическому? Чтобы ответить на этот вопрос, нам необходимо перечислить различные возможные переходы между аттракторами — задача столь же необходимая, как и идентификация аттракторов».
К последнему абзацу примыкают и слова Видаля, одного из авторов цитируемой книги, сказанные им в «Заключительной дискуссии»: «Прежде всего мне хотелось бы затронуть один принципиально важный аспект, не получивший должного развития в книге: область, в пределах которой теория динамических систем верна и применима, до сих пор остается неопределенной. Мы располагаем описаниями отдельных событий и последовательностей событий, приводящих к хаотическим ситуациям: из таких описаний состоит вторая часть книги. Это означает, что при определенных условиях мы в состоянии предсказать, каким образом возникнет апериодический режим, т.е. произойдет переход. Но теория ничего не говорит о том, сочетание каких условий гарантирует, что данная последовательность событий завершится установлением хаотического режима. Теория не определяет (по крайней мере в существующем ныне виде) предпосылки хаотического режима, и это, несомненно, следует отнести к числу ее недостатков».
Достоинство рекурсивной функции ax cos(x) состоит в том, что она проливает яркий свет на некоторые темные места, о которых говорится в данных отрывках. В частности, она позволяет ясно понять, почему рекурсивные функции оказываются чувствительными к начальным, а в нашем случае лучше говорить — к граничным условиям. Рекурсивные функции ведут себя вполне предсказуемо, если не удаляться в области, труднодоступные для наших вычислительных средств, где компьютер работает на пределе своих возможностей. Поскольку рассмотренные рекурсивные функции изначально детерминированы, «хаосу» просто неоткуда взяться и, следовательно, эффекты, приводящие к непредсказуемым результатам, проистекают не от самих математических выражений, а только от нас: какие начальные или граничные условия мы выбираем и какими вычислительными системами и компьютерными процессорами мы пользуемся. Когда мы изучаем динамические процессы, эту простую и понятную мысль нужно постоянно помнить, чтобы не скатиться на теологические позиции.
Кроме того, если иметь в виду нашу тригонометрическую функцию, необходимо будет сделать уточнение в отношении ее чувствительности к начальным условиям. Дело в том, что в местах возникновения аттракторов рекурсивная функция как раз нечувствительна к начальным условиям, под которыми следует понимать значения переменной x и коэффициента a. Орбиты рекурсивных функций, т.е. последовательности мод f 1, f 2, …, f n, в определенных пределах изменения x и a более чем предсказуемы, поскольку заранее известны вид, род и класс аттрактора. Кажущееся случайным соскальзывание орбит на аттрактор-плюс или аттрактор-минус в действительности не является таким уж принципиально «непредсказуемым», и, следовательно, «хаотическим». Более мощные, чем у нас, вычислительные системы и 32-разрядный процессор отодвинут границы «непредсказуемости», возникшие в системе MATLAB v. 4.0 с 16-разрядным процессором, которым мы пользовались. Другое дело, когда рекурсивная функция при данных значениях переменной x и коэффициента a не образует аттрактора. В этом случае возникает быстрая потеря верных знаков в амплитуде моды, и орбита рекурсивной функции по-настоящему становится хаотичной. Эта потеря верных знаков возникает не потому, что мы или кто-то другой, подобно Лоренцу, субъективно решили «слегка изменить значения, уменьшив число верных десятичных знаков», а в силу математической природы рекурсивной функции, т.е. абсолютно объективно. Таким образом, сожаления, прозвучавшие в «Заключительной дискуссии», нам не совсем понятны. Во всяком случае, в отношении рекурсивной функции ax cos(x) всегда можно более или менее точно предсказать (опять-таки здесь все зависит от используемых вычислительных средств), в каком месте оси абсцисс, при каком коэффициенте a и на какой моде орбита примет хаотический вид.
Далее остается нерешенным весьма трудный вопрос: является ли физический хаос, скажем, турбулентное движение жидкости, возникшее за винтом судна, или сложное движение языков пламени, вырывающихся из сопла ракетного двигателя, тем же самым, что и математический хаос, внесенный людьми или машинами в процессе вычисления рекурсивной функции? Сложная траектория движения снежинок при порыве ветра или песчинок при обвале песчаного берега, подмытого половодьем, это еще не повод, чтобы их динамику считать принципиально непредсказуемой. Словом «хаос», как и словом «бифуркация», обозначают широкий круг физических и математических явлений, мало заботясь об их различии. Напротив, наблюдается тенденция к объединению самых разнообразных процессов и явлений в рамках некой единой и универсальной теории «хаоса и порядка», которой в действительности не существует. Разумеется, динамика реальных конвекционных потоков описывается дифференциальными уравнениями, но какое отношение имеет видимая хаотичность протекания динамического процесса к отбрасыванию верных десятичных знаков при подсчете амплитуды колебаний, непонятно. В цитируемых книгах отсутствует внятный текст, который бы убедительно рассказал всем о тесной взаимосвязи между математическими манипуляциями и объективно наблюдаемыми в природе физическими явлениями.
Что же касается этого учебника, то мы не ставили перед собой задачу выяснить связь между математикой и физикой. Более того, мы целиком отвлекаемся от физической стороны проблемы и пытаемся решить задачу исключительно в математической плоскости. Нас не будут интересовать физические явления, которые чаще всего обозначаются словом «турбулентность». Если эти явления и называть «хаотичными», то мы имеем в виду совершенно другую «хаотичность», а именно ту, что возникает в процессе вычисления конкретной рекурсивной функции, и не более того.
До конца неясна связь фракталов с хаосом. Во Введении к первой главе Кроновер пишет: «Термин фрактал относится к некоторой статичной геометрической конфигурации, такой, как мгновенный снимок водопада. Хаос — термин динамики, используемый для описания явлений, подобных турбулентному поведению погоды». Вот другая выдержка: «Интуитивно понятно, что динамической противоположностью фрактала является хаос. Это означает, что хаос описывает состояние крайней непредсказуемости, возникающей в динамической системе, в то время как фрактальность описывает крайнюю иррегулярность или изрезанность, присущую геометрической конфигурации». Такое представление о фрактале и его связи с хаосом, быть может, и имеет право на существование, только ведь оно заметно расходится с тем, что об этом говорилось в других частях цитируемого учебника. Пусть фрактал — это нечто, относящееся к статическому, а хаос — к динамическому, но раньше подчеркивалась либо дробная размерность фрактала, либо подобие его частей целому. Каким образом эти качества можно сочетать с непредсказуемостью хаотических процессов и чувствительностью их к начальным условиям?
В связи с такой терминологической двусмысленностью не лишним будет еще раз определиться в отношении этих двух терминов. Коль скоро наша рекурсивная функция настойчиво демонстрирует фрактальную природу в виде подобия отдельных мод и аттракторных комплексов, мы оставляем за термином «фрактальность» свойство статической структуры или динамического процесса быть подобными самим себе в частях и целом. Нет принципиального различия между статической и динамической структурами; в этом убеждают нас многочисленные графики аттракторов и, в частности, аттрактор «Крепостная стена». Если и проводить противопоставление, то хаосу нужно ставить в оппозицию не фрактал, а аттрактор. Мы знаем, что аттракторы возникают в местах отсечения низшими модами максимумов или минимумов у высших мод. Если в местах экстремумов высших мод не оказывается подходящей низшей моды, то там в качестве альтернативы стремительно развиваются хаотические процессы в виде потери верных знаков в величине амплитуды высших мод. «Хаотическая» или «шумовая» составляющая моды тем выше, чем меньше верных знаков в ее амплитуде. В местах аттрактора амплитуда мод содержит наименьшее число неверных знаков; но в эпицентре хаоса амплитуда мод может не иметь ни одного верного знака. Такое понимание хаоса вытекает из свойств именно тригонометрической функции ax cos(x), которую мы сейчас подробно анализируем, т.е. оно не претендует на общее и универсальное положение. Но оно вполне согласуется с пропагандируемым нами конструктивным подходом в изучении предмета, когда во главу угла ставятся конкретные свойства объекта, а не его абстрактное осмысление или, что еще хуже, какие-то туманные философские реминисценции.
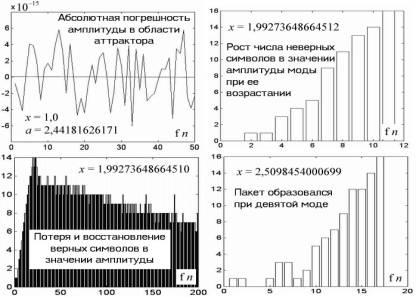
Посмотрим на рис. 4.98. В левом верхнем углу приведен график абсолютной погрешности амплитуды моды в области действия Большого аттрактора. Абсолютная погрешность амплитуды вычислялась как разность величин, подсчитанных на 16-разрядном и 32-разрядном процессорах. График показывает, что с ростом порядка моды эта разность не выходит за пределы ± 6 · 10 – 15, т.е. ошибка возникает в самом последнем знаке числа, характеризующего амплитуду, и не растет с увеличением порядка моды. В правом верхнем углу данного рисунка размещена диаграмма, на которой виден рост числа неверных знаков в значении амплитуды моды при росте ее порядка в точке x = 1,99273648664512, т.е. в той самой точке вблизи границы Большого аттрактора, где орбита рекурсивной функции удаляется на бесконечно большие расстояния (эта орбита показана на левом нижнем графике рис. 4.96). Число неверных знаков в величине амплитуды, подсчитанной 16-разрядным процессором, как в предыдущем, так и в последующем случаях, определялось вторичным подсчетом этой же самой амплитуды 32-разрядным процессором. Диаграмма показывает, что все 16 значащих символов в амплитуде моды f 12 становятся неверными. Чтобы подтвердить, что рост числа неверных знаков будет наблюдаться и в других частях оси абсцисс, которые не попали под действие аттрактора, аналогичная диаграмма рассчитывалась для точки с координатой x = 2,50984540006999. В этой области амплитуда мод слегка колеблется, но вплоть до моды f 8 там не возникает характерного модуляционного пакета биений с резко выделяющимися максимумами и минимумами; такой пакет появляется только при моде f 9. После этого начинает неуклонно расти число неверных знаков в величине амплитуды, так что амплитуда моды f 17 оказывается полностью ошибочной.
Рис. 4.98
Самым удивительным из всех приведенных графиков является тот, что расположен в левом нижнем углу рис. 4.98, где показана быстрая потеря и затем медленное восстановлении верных знаков в величине амплитуды после попадания орбиты на аттракторные уровни. В точке x = 1,99273648664510, т.е. чуть-чуть левее границы Большого аттрактора, где орбита захватывается аттрактором-минус (см. левый верхний рис. 4.95), сначала наблюдается стремительный рост неверных знаков. В значении амплитуды моды f 12 четырнадцать символов оказываются ошибочными. Казалось бы, подстановка ошибочного значения, полученного в предыдущей моде, в качестве аргумента для последующей моды даст еще более ошибочный результат. Но происходит, на первый взгляд, странное: ошибочная переменная при подстановке ее в функцию ведет, пусть к очень медленному, но все же исправлению ошибки, которая накопилась на первых этапах рекурсии. Из диаграммы видно, что из 14 неверных знаков по достижению моды f 200 амплитуда стала содержать всего 6 ошибочных символов, 8 символов аттрактору удалось каким-то образом исправить. Если перечислять самые примечательные качества аттрактора, то его способность восстанавливать утраченную числовую информацию нужно поставить на первое место. Рано или поздно амплитуда мод асимптотически стремится на аттракторные уровни; в этом свойстве тоже проявляется притягательное действие аттрактора.
Нужно особо отметить, что вычисления, произведенные с помощью 16-разрядного процессора, принципиально не отличаются от вычислений, произведенных 32-разрядным процессором. Чтобы в этом убедиться, вернемся к квазиаттракторам, которые рассматривались в подразделе 12. В конце этого подраздела был задан вопрос, почему максимальная мода, которую мы рассматривали, имеет 28-й порядок? Оказывается, начиная с моды f 29 16-разрядный процессор отказывается нормально работать. Все дело в вычислении косинуса рекурсивной функции ax cos(x). Для нахождения косинуса вычислительная система раскладывает его в степенной ряд и подсчитывает величину тригонометрической функции по определенному количеству членов этого ряда. Вначале, когда величина аргумента тригонометрической функции мала, значение косинуса подсчитывается с удовлетворительной точностью. Но потом, когда аргумент приближается к одному миллиарду, точность подсчета косинуса неожиданно быстро падает.
Взгляните на табл. 4.12, где приведены числовые значения моды f n, подсчитанные при коэффициенте a = 2,0 и переменной x = 3,419157788078807, а также погрешность вычисления δ, точнее, абсолютное значение разности мод f n, подсчитанных 16-разрядным и 32-разрядным процессорами. В последней графе табл. 4.12 приведены значения косинуса моды, подсчитанные 16-разрядным процессором. Из этой таблицы видно, что косинус постепенно приближается к единице и держится на единичном значении до моды f 28. Потом происходит срыв, при котором значение косинуса резко отклоняется от единицы и погрешность вычислений, до этого момента остававшаяся в допустимых границах, подскакивает до неприемлемой величины.
Таблица 4.12
| Мода f n | Значение f n | Погрешность | δ | | cos (f n) |
| f 1 | – 6,576582313750390 | 3,9649 × 10 – 15 | 0,95726696689742 |
| f 2 | – 12,59109000807007 | 5,6182 × 10 – 15 | 0,99969449134447 |
| f 3 | – 25,17448664218018 | 7,9871 × 10 – 15 | 0,99912878675893 |
| f 4 | – 50,30510859216090 | 4,4447 × 10 – 15 | 0,99921498745237 |
| f 5 | – 100,5312369014119 | 5,3262 × 10 – 14 | 0,99999996301166 |
| f 6 | – 201,0624663658569 | 1,1914 × 10 – 14 | 0,99999985606450 |
| f 7 | – 402,1248748516625 | 8,0557 × 10 – 14 | 0,99999948469247 |
| f 8 | – 804,2493352673764 | 6,5785 × 10 – 14 | 0,99999869435569 |
| f 9 | – 1608,496570407609 | 2,0336 × 10 – 14 | 0,99999935954882 |
| f 10 | – 3216,991080488150 | 6,0704 × 10 – 13 | 0,99999997935240 |
| f 11 | – 6433,982028130014 | 5,8623 × 10 – 13 | 0,99999996257751 |
| f 12 | – 12867,96357470874 | 5,1522 × 10 – 12 | 0,99999999784800 |
| f 13 | – 25735,92709403365 | 3,3579 × 10 – 12 | 0,99999999712520 |
| f 14 | – 51471,85404009622 | 7,2160 × 10 – 12 | 0,99999999999323 |
| f 15 | – 102943,7080794950 | 2,3468 × 10 – 12 | 0,99999999997779 |
| f 16 | – 205887,4161544175 | 1,3901 × 10 – 11 | 0,99999999996166 |
| f 17 | – 411774,8322930472 | 1,9674 × 10 – 11 | 0,99999999999851 |
| f 18 | – 823549,6645848679 | 5,7791 × 10 – 11 | 0,99999999999752 |
| f 19 | – 1647099,329165658 | 1,0038 × 10 – 10 | 0,99999999999993 |
| f 20 | – 3294198,658331088 | 4,4640 × 10 – 10 | 0,99999999999987 |
| f 21 | – 6588397,316661297 | 7,5752 × 10 – 10 | 0,99999999999999 |
| f 22 | – 13176794,63332244 | 4,1164 × 10 – 9 | 0,99999999999999 |
| f 23 | – 26353589,26664457 | 1,6462 × 10 – 9 | 1,00000000000000 |
| f 24 | – 52707178,53328914 | 3,2925 × 10 – 9 | 1,00000000000000 |
| f 25 | – 105414357,0665783 | 2,6586 × 10 – 8 | 1,00000000000000 |
| f 26 | – 210828714,1331566 | 5,3182 × 10 – 8 | 1,00000000000000 |
| f 27 | – 421657428,2663131 | 6,4372 × 10 – 9 | 1,00000000000000 |
| f 28 | – 843314856,5326260 | 1,8661 × 10 – 7 | 1,00000000000000 |
| f 29 | – 1686629713,065233 | 1,9371 × 10 – 5 | 0,99999999999999 |
| f 30 | – 3373259425,465595 | 0,6649 | 0,99999999980290 |
| f 31 | – 5309321708,940010 | 1,4372 × 10 + 9 | 0,78697204087812 |
| f 32 | + 9942824875,132380 | 3,5502 × 10 + 9 | – 0.93635547252583 |
Истинные значения двух последних мод вполне предсказуемы; они равны:
f 31 = 2 · f 30 = – 6746518852,261, f 32 = 2 · f 31 = – 13493037704,522,
но произошел сбой в вычислениях. Аналогичный сбой на этом квазиаттракторе будет наблюдаться для числовых значений мод, подсчитанных 32-разрядным процессором, только произойдет он позже, а именно, на моде f 70. Сначала тригонометрическая функция приближается к единице, когда, наконец, косинус от моды f 51 не становится равным в точности единице; затем это значение держится до моды f 69, после чего происходит ее сбой. На числах этот сбой выглядит следующим образом:
f 70 = – 3708937962535486895300,77494117638;
cos (f 70) = 0,999999999999999999999999999727566;
f 71 = – 7417875925070973790601,54988033187;
cos (f 71) = 0,999999999997958012246740921382067;
f 72 = – 14835751850081358734026,4004727902;
cos (f 72) = – 0,848074987937728445542481429190518;
f 73 = 25163660142609761556265,1231090243.
Можно спрогнозировать, что примерно на моде f 150 откажется считать 64-разрядный процессор, а вскоре после f 300 — 128-разрядный и т.д. Таким образом, квазиаттракторы могут использоваться в качестве тестов для определения вычислительных возможностей процессоров. Далее попытаемся проследить в деталях, как зарождается хаос. С этой целью мы привели несколько рисунков, на которых поэтапно зафиксирован рост хаотической составляющей в амплитуде мод возрастающего порядка. Первыми в этом ряду стоят два рис. 4.99 и 4.100, где показаны моды f 7 и f 8, соответственно.
Рис. 4.99
Рис. 4.100
Большее число знаков в их амплитуде уже ошибочно, но визуально это определить пока трудно. Вблизи точки x = 2,137 никакого аттрактора не возникает, следовательно, в этой зоне будут нарастать хаотические процессы с несколько большей скоростью, чем в прилегающих областях. При коэффициенте a = 2,44181626171 моды принимают небольшие значения — f 7 = –15, f 8 = 27. На рис. 4.101 отчетливо видны следы шума: теперь амплитуда моды f 12 изменяется не непрерывно, а дискретно; скачки амплитуды составляют несколько единиц. В моде f 13 вообще трудно узнать тригонометрическую функцию косинуса, особенно в эпицентре хаоса, т.е. возле точки x = 2,1369607273, где скачки амплитуды составляют уже несколько десятков единиц. Вдали от этого эпицентра, около точки x = 2,1369607354, еще можно узнать характерные биения.
Рис. 4.101
Аналогичная картина наблюдается и в других экстремальных точках, где отсутствуют аттракторы. Проведем числовой анализ значений «шумящих» амплитуд вблизи точки x = 2,798964517. На рис. 4.102 при различных масштабах показана мода f 8, которая в указанной точке имеет пик высотой 23,511. Если смотреть на эту моду «издали» (два левых графика), то можно ничего и не заметить. Но при большом увеличении изображения видно, что амплитуда вершины пика изменяется дискретным образом. В правом нижнем углу рис. 4.102 показана самая «макушка» пика, имеющая вид гребенки, состоящей из отдельных импульсов, которые очерчивают три уровня. Первый уровень соответствует значению 23,51158, второй — 23,51152 и третий — 23,51146. Импульсы отстоят друг от друга на крохотные расстояния; одни импульсы встречаются чаще других. Если в центральной части взять сто значений амплитуды, то 18 из них будут иметь значение первого уровня, 74 — второго и 8 — третьего уровня. Впрочем, все зависит от того, как считать. Вероятность попадания того или иного значения непрерывно меняется в зависимости от переменной x. Основной вопрос звучит так: почему не встречаются значения амплитуды, равные, скажем, 23,51157 или 23,51141? Чтобы ответить на этот вопрос, мы привели табл. 4.13, в которой даны значения мод в трех рядом стоящих точках, где амплитуда принимает три различных значения. Эти три значения на данном участке оси x встречаются с вероятностью P1 = 0,18, P2 = 0,74 и P3 = 0,08.
Рис. 4.102
Таблица 4.13
| Рi | 0,18 | 0,74 | 0,08 |
| x | 2,7989645192 | 2,7989645194 | 2,7989645195 |
| f 1 | –6,43729817307363 | –6,43729817306903 | –6,43729817306673 |
| f 2 | –15,53240287329676 | –15,53240287329676 | –15,53240287329676 |
| f 3 | 37,34428677616851 | 37,34428677616849 | 37,34428677616847 |
| f 4 | 85,50754519349842 | 85,50754519349769 | 85,50754519349697 |
| f 5 | –161,7541091132794 | –161,7541091133737 | –161,7541091134680 |
| f 6 | 14,97087610069801 | 14,97087606348619 | 14,97087602626316 |
| f 7 | –27,06723651058457 | –27,06723552898865 | –27,06723454709679 |
| f 8 | 23,51158215456263 | 23,51152066883408 | 23,51145916455040 |
| f 9 | –2,89015172956695 | –2,89366963594595 | –2,89718857456540 |
| f 10 | 6,83530470055992 | 6,84976668762797 | 6,86416294800448 |
| f 11 | 14,21058872054075 | 14,11230117081779 | 14,01098438136545 |
| f 12 | –2,54542140192324 | 0,85677735725714 | 4,30554245724057 |
| f 13 | 5,14323276972669 | 1,37006211352120 | –4,16029019182808 |
| f 14 | 5,24503974672874 | 0,66704344101581 | 5,32796893537363 |
| f 15 | 6,50384859268244 | 1,27967164489049 | 7,51234633459589 |
| f 16 | 15,49612356096316 | 0,89688851314587 | 6,14568247309669 |
| f 17 | –36,99283122556097 | 1,36668000648767 | 14,86498540975506 |
| f 18 | –68,72112107634469 | 0,67645303757940 | –24,14667901296889 |
| f 19 | –154,9526610980709 | 1,28805029449219 | –32,54557236513742 |
| f 20 | 199,7551834169275 | 0,87748598322535 | –33,93223979457752 |
Из табл. 4.13 видно, что мода f 8 принимает три значения потому, что мода f 3, в свою очередь, на этом участке оси x могла принять только три значения, которые при подсчете 16-разрядным процессором на конце давали три комбинации цифр: 51, 49 и 47. Эти цифры в зависимости от значения x выпадали почти случайно. Например, предыдущая мода f 2 на продолжительном участке оси абсцисс принимает одно и то же значение, равное –15,53240287329676 (в табл. 4.13 оно выделено особо). Таким образом, случайные значения моды f 3, вызванные тепловыми процессами, протекающими внутри микросхем компьютера, определили дальнейшую эволюцию мод, которая носила уже действительно хаотический характер. Когда орбита достигла моды f 8, за счет экспансии хаоса, верных цифр в значении этой моды осталось только пять, а именно: 23,511, все высшие порядки (в табл. 4.13 они подчеркнуты) оказались ошибочными. По достижении орбиты моды f 12 не осталось ни одной верной цифры в числе; все значения мод с f 12 по f 20 ошибочны.
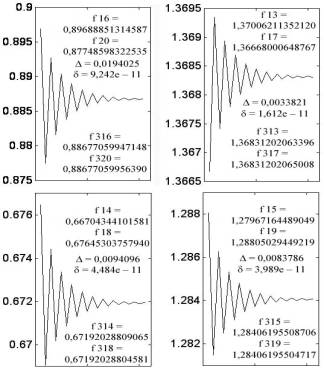
Когда при x = 2,7989645194 и a = 2,44181626171 орбита вышла на аттракторные уровни, удобно произвести классификацию всех мод по четырем группам, чтобы можно было видеть, с какой скоростью и по какой траектории амплитуды мод притягиваются к своим четырем уровням. На рис. 4.103 приведены четыре орбиты и соответствующие разности значений между первыми двумя значениями мод, вышедшими на положительные аттракторные уровни, а также приведены разности значений мод, которые старше исходных на три сотни порядков. Так, для орбиты, устремленной к уровню 0,887 (левый верхний график), имеем две разности:
Δ = | f 16 – f 20 | = 0,0194025; δ = | f 316 – f 320 | = 9,242e –11.
Рис. 4.103
В табл. 4.14 приведены значения мод в двух точках оси x, подсчитанные 32-разрядным процессором. При x = 2,7989645195 орбита выходит на уровни аттрактора-плюс, а при x = 2,79896451701 — на аттрактор-минус. Из табл. 4.13 видно, что на аттрактор-плюс орбита вышла при x = 2,7989645194, а при x = 2,7989645195 она удалится на бесконечно большие значения. Если считать 32-разрядным процессором, то на бесконечность орбита выйдет при значениях оси абсцисс x = 2,7989645194 и x = 2,7989645171. На аттрактор-плюс попадаешь еще при x = 2,79896451700 и т.д., т.е. на аттракторы первого рода в этой области, как, впрочем, и других, натыкаешься достаточно часто.
Таблица 4.14
|
x |
2,7989645195 |
2,79896451701 |
| f 1 | –6,43729818900353132042550115618529 | –6,43729817755937139147562022470369 |
| f 2 | –15,5324028732967624908415416624452 | –15,5324028732967632565838494405688 |
| f 3 | 37,3442867761685096684298286797323 | 37,3442867761685165820554378053863 |
| f 4 | 85,5075451934984363712789147196992 | 85,5075451934986712325481676782559 |
| f 5 | –161,754109113276728553614560496586 | –161,754109113246165437881966282704 |
| f 6 | 14,970876101745756921449632404858 | 14,9708761138058839865047393626794 |
| f 7 | –27,0672365382228100022514548566509 | –27,0672368563522026835103564399088 |
| f 8 | 23,5115838857813134606640869005617 | 23,5116038129357102414945432062546 |
| f 9 | –2,89005267745272078491469478186433 | –2,88891253860830245717157598290967 |
| f 10 | 6,83489649228403546691947336995501 | 6,83019384555230139614543229444763 |
| f 11 | 14,2133121462172460334586605451252 | 14,2444849840412889823588221222457 |
| f 12 | –2,64016503464145433890536926396538 | –3,72561966402650197038867162557821 |
| f 13 | 5,65317923961842800750081570058658 | 7,58939541816279630566912820089063 |
| f 14 | 11,1539825784743061633059091598856 | 4,84627781430524352866065730785301 |
| f 15 | 4,29638334886135865236046539847677 | 1,57967348358334344449059629142946 |
| f 16 | –4,23950937359064438092058556090353 | –0,0342411621470919324381567971066428 |
| f 17 | 4,71488360517233750900129781745356 | –0,0835616163994955481893893204414759 |
| f 18 | 0,0287202846875940062004182645048334 | –0,203330161701791586560386759170322 |
| f 19 | 0,0701007367882597810725201600769185 | –0,486266873902493495421383720317056 |
| f 20 | 0,17075270920122834690674473378539 | –1,04973821333291680950351981634747 |
| f 21 | 0,410883145049125934379184278746214 | –1,27598988783232928208778077387219 |
| f 22 | 0,91979482111563251071392740167651 | –0,905290654634657497920993052594477 |
| f 23 | 1,36102047287495594470345084970718 | –1,36492164302330327014685939264458 |
| f 24 | 0,692059122893920876412156570675595 | –0,681320437861449238156249441558443 |
| f 25 | 1,30109645424402625483511276957547 | –1,29223367017999177052452424005569 |
| . . . | Выход на уровни аттрактора-плюс | Выход на уровни аттрактора-минус |
В табл. 4.15 приведены изменения вероятности моды f 3 в зависимости от координаты x. Ранее говорилось, что значение амплитуды f 3 = 37,...51 можно обнаружить на участке от x = 2,7...145 до x = 2,7...195 с вероятностью P1 = 0,18; f 3 = 37,...49 — с вероятностью Р2 = 0,74 и f 3 = 37,...47 — с вероятностью P3 = 0,08. Теперь ось x в зоне с точкой x = 2,798964517 по середине была поделена на отрезки в пять раз меньшие и на каждом таком отрезке бралось 100 значений f 3. Значение f 3 = 37,...51 на участке с координатой левой границы, равной x = 2,798964516, встречается 31 раз, что соответствует вероятности P = 0,31. В табл. 4.15 указываются последние две цифры; так, число 31 стоит на пересечении строки 51 и столбца 16. Далее, к примеру, значение амплитуды моды f 3 = 37,...43 на участке с координатой левой границы, равной x = 2,798964524, встречается 42 раза, что соответствует вероятности P = 0,42 (число 42 стоит на пересечении строки — 43 и столбца — 24) и т.д. Аналогичные таблицы могут быть составлены для мод f 4, f 5, ..., f 12, ... и на всех участках вероятности соответствующих импульсов будут неизменными.
Таблица 4.15
| f 3 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 51 | 31 | 32 | 26 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 49 | 68 | 67 | 72 | 67 | 34 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 47 | 1 | 1 | 2 | 23 | 64 | 56 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 45 | 0 | 0 | 0 | 0 | 2 | 39 | 64 | 11 | 0 | 0 | 0 | 0 | 0 | 0 |
| 44 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 54 | 5 | 0 | 0 | 0 | 0 | 0 |
| 43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 35 | 42 | 0 | 0 | 0 | 0 | 0 |
| 41 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 45 | 18 | 0 | 0 | 0 | 0 |
| 39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 58 | 2 | 0 | 0 | 0 |
| 38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 38 | 0 | 0 | 0 |
| 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 42 | 3 | 0 | 0 |
| 35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 | 36 | 0 | 0 |
| 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 48 | 7 | 0 |
| 31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 34 | 0 |
| 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 45 | 3 |
| 28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 31 |
| 27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 37 |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 28 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Обратите внимание, импульсов со значениями амплитуды моды f 3, оканчивающихся на цифры 50, 48, 46, 42, 40, 37 и т.д., просто не существует. Поэтому, например, моду f 12 = –2,5 на участке от x = 2,...45 до x = 2,...95 можно обнаружить с вероятностью Р1 = 0,18; f 12 = 0,8578 (один из аттракторных уровней) можно обнаружить с вероятностью P2 = 0,74 и f 12 = 4,3 — с вероятностью Р1 = 0,08. Каких-то промежуточных значений амплитуды для моды f 12, как это видно по рис. 4.104, здесь быть не может. На данном рисунке мы также видим, что импульс в области с координатой x = 2,798964517 посередине опустился ниже оси абсцисс, если можно так сказать, лишь на 18 %. Использование понятия вероятности в данном случае не совсем правомерно, так как хаотический процесс принял вполне детерминированный характер. Единственное, о чем здесь нужно не забывать, так это об истинном значеним моды (т.е. об истинных первых 16 знаках от значения, приведенного в табл. 4.14), посчитанном 32-разрядным процессором для точки x = 2,79896451701, равно f 12 = –3,7, а для точки x = 2,7989645195 имеем f 12 = –2,6.
Рис. 4.104
При коэффициенте a = 2,44181626171 можно наблюдать формирование аттракторов второго рода и нарастание хаоса одновременно. На рис. 4.105, где показаны моды f 12 и f 13, шумовая составляющая еще больше увеличилась, однако распределение вероятностей для соответствующих импульсов нисколько не изменилось. В частности, «пойманная» аттрактором-плюс вероятность равна по-прежнему P2 = 0,74.
Рис. 4.105
На рис. 4.106 приведен график моды f 16; все ее линии расплылись и приняли дискретный характер. Это особенно хорошо видно в левом нижнем окне, где показан аттрактор первого рода, сформировавшийся в условиях шума и потому расплывшийся. В правом нижнем окне показана гребенка импульсов с неизменной вероятностью их появления. Уровень с вероятностью P2 = 0,74 остается аттракторным. На рис. 4.107 можно увидеть аттракторные уровни у моды f 94. Чуть левее и правее эпицентра хаоса, т.е. зоны с точкой x = 2,798964517, произошел захват орбиты аттрактором-минус, и мода f 94 здесь принимает значение, равное примерно 0,88. Несколько дальше от эпицентра хаоса можно увидеть еще несколько мест, где амплитуда принимает аттракторные значения. Для сравнения слева на этом рисунке оставлен аттрактор первого рода. В двух нижних окнах рис. 4.107 изображена орбита захвата амплитуды мод с вероятностью 0,74 аттрактором-плюс. В третьем окошке сбоку показан аттракторный уровень с этой вероятностью высотой 0,67.
Рис. 4.106
Рис. 4.107
Захват аттрактором одного или двух уровней из трех говорит о том, что шумовой аттрактор в действительности является полупрозрачным, поскольку он держит амплитуды мод на аттракторном уровне не на все 100 %. На рис. 4.108 продемонстрировано четыре эпизода с полупрозрачными аттракторами. Два левых окошка, где изображены моды f 98 и f 99, отвечают одним и тем же границам по оси x: x = 2,7989644408 ± 4,0е – 10. В этой области при коэффициенте a = 2,44181626171 наряду с полупрозрачными аттракторами первого рода существует полупрозрачный аттрактор второго рода с уровнями +3,4 и – 8,0. В центре этого аттрактора амплитуды мод удерживаются на аттракторных уровнях на все 100 %, но по бокам этого нет. В области x = 2,7989644725 ± 2,0е – 9, которая показана в двух правах окошках, расположен полупрозрачный аттрактор второго рода с уровнями –3,4 и + 8,0. Он шире, возник раньше предыдущего, следовательно, зона, где амплитуда мод захватывается аттрактором на все 100 %, тоже будет шире. Мы сравнили две пары мод: f 26, f 27 и f 96, f 97. Как видим, графики различаются немногим, во всяком случае, вблизи оси абсцисс. Это говорит о том, что хаотические процессы к тридцатой моде вполне сложились и дальнейший рост порядка моды уже не может существенно повлиять на общую картину хаоса.
Рис. 4.108
Рис. 4.109
Если посмотреть на эпицентр хаоса «издали», он будет выглядеть так, как это показано на рис. 4.109, где изображен график моды f 17. Здесь все прямоугольные импульсы, и положительные и отрицательные, как бы прикреплены к оси абсцисс. Такое впечатление возникает потому, что вдоль всей оси x действует полупрозрачный аттрактор первого рода. С ростом порядка мод амплитуда некоторых пиков достигает астрономических величин, так что компьютер не в состоянии отобразить их на экране дисплея. В окне рис. 4.109 показана мода f 100; многие шумовые импульсы здесь не видны не потому, что они слишком малы относительно выбранного масштаба (единицы, стоящие по оси ординат, нужно умножать на 1010), а потому, что они слишком огромны (больше 1020).
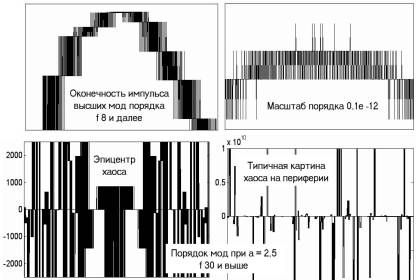
Рис. 4.110
Типичная картина хаоса независимо от того, в какой области оси абсцисс мы находимся, показана на рис. 4.110. В эпицентре хаоса отдельные импульсы, если на них смотреть в «микроскоп», выглядят как импульс, показанный в левом верхнем окне. При еще большем «увеличении», порядка 0,1е–12, которому отвечает правое верхнее окно, становятся различимы отдельные импульсы, из которых состоят прямоугольники, показанные в предыдущем окне. Большая или меньшая густота гребенки импульсов зависит от шага, с которым мы проходим данный участок оси абсцисс. Но в любом случае, частота импульсов будет оставаться пропорциональной вероятности появления этих импульсов. В двух нижних окнах рис. 4.110 показан эпицентр хаоса и его периферия, когда коэффициент a приближается к 2,5, а мода достигает примерно 30-го порядка. Графики мод рекурсивной функции ax cos(x) на всем протяжении оси абсцисс состоят из бесконечного числа прямоугольных импульсов либо хаотической, либо аттракторной природы, либо смешанной, когда аттракторные уровни часть хаотических амплитуд притягивают на себя, а часть отпускают от себя, и они устремляются на бесконечные расстояния от нулевого уровня.
Что же получается: если мода достигла, скажем, сотого порядка, то на оси абсцисс вне аттракторов безнадежно искать участки с гладкими, непрерывно меняющимися линиями; везде господствует дискретность? Нет, это не так, и последний рисунок из нашей серии, а именно, рис. 4.111, тому подтверждение. Этот рисунок запечатлел моду f 201, которая изоморфна (≈) начальному участку моды f 4. В самом деле, сравните моду f 201 с модой, изображенной в левом нижнем окне рис. 4.45. Они различаются только масштабом, который можно выразить следующей пропорцией:
Δx(f 4)/Δx(f 201 ≈ f 4) = 16400000/3.
Рис. 4.111
Откуда было взяться моде f 201 ≈ f 4, которую шумовые процессы даже не коснулись? Всмотритесь, все изгибы кривой f 201 ≈ f 4 меняются непрерывно, элементы дискретности практически отсутствуют. Как это могло получиться?
Дело в том, что на участке в районе точки x = 3,43113702 при коэффициенте a = 2,44177555066794 существует аттрактор 2-го рода с уровнями +3,4 и – 8,0, границы которого с ростом порядка мод постоянно сужаются. Окно в центре рис. 4.111 показывает правую границу этого аттрактора, которая при переходе мод от f 198 к f 199 отступила влево на дискретную величину, породив пакет мод из f 1 и f 2. Ниже кривой f 201 ≈ f 4 фрагментарно показаны графики еще пяти мод (f 196 – f 200), которые поясняют, как дискретные уровни аттрактора 2-го рода, представленные модами f 196 и f 197, становятся непрерывными функциями, представленными модами f 199 ≈ f 2 и f 200 ≈ f 3. Поскольку аттракторные уровни не подвержены шумовым процессам, то все моды, возникшие на месте аттракторных уровней, выглядят как «новенькие». Какой бы большой порядок мода ни имела, у нее всегда можно найти вблизи границ аттракторов гладкие участки кривой. Впоследствии эти участки будут подвержены коррозии хаоса и на их месте окажутся шумовые импульсы прямоугольной формы. Но до этого гладкие моды высоких порядков успеют породить новые системы аттракторов, которым шумы не страшны. Этот процесс бесконечен: с ростом порядка мод на микроскопических пространствах постоянно воспроизводится все то, что нами было рассмотрено на больших пространствах. В этой бесконечной череде подобных форм проявляется фрактальная природа тригонометрической функции ax cos(x).