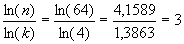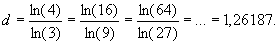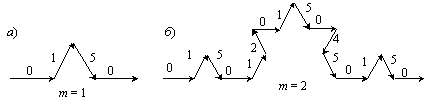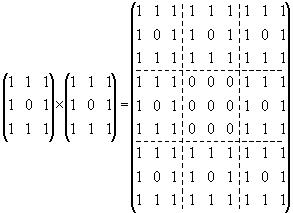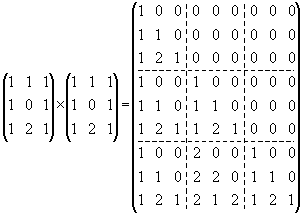Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
4.2. Прямое произведение и фракталы
На рис. 4.1 изображены: деление единичного отрезка на 3 части (а), единичной квадратной площадки на 9 частей (б), единичного куба на 27 частей (в) и на 64 части (г). Если число частей обозначить через n, коэффициент масштабирования или подобия — через k, а размерность пространства — через d, то в соответствии с приведенными рисунками имеем следующие соотношения: n = kd, где
если n = 3, k = 3, то d = 1; если n = 9, k = 3, то d = 2; если n = 27, k = 3, то d = 3.
а
б
в
г

Рис. 4.1
При уменьшении линейных размеров в 4 раза согласно приведенному соотношению, имеем: если n = 4, k = 4, то d = 1; если n = 16, k = 4, то d = 2; если n = 64, k = 4, то d = 3. Во всех случаях размерность пространства выражается целыми числами: d = 1, 2, 3; в самом деле, для n = 64 (рис. 4.1г), величина d равна
На рис. 4.2 показано пять шагов построения ломаной Коха: первоначально берется отрезок единичной длины (а), делится на три части (k = 3) и из четырех частей (n = 4) составляется ломаная (б); затем каждый прямой отрезок вновь делится на три части (k2 = 9) и из 16 частей (n2 = 16) составляется ломаная (в); процедура повторяется для k3 = 27 и n3 = 64, в результате получается ломаная (г); наконец, при k5 = 243 и n5 = 1024 получаем ломаную (д).
а
б
в
г
д
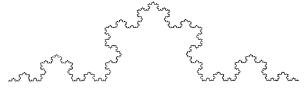
Рис. 4.2
Если следовать вышеприведенному соотношению для размерности пространства, то получим следующий ряд отношений:
Таким образом, здесь мы можем говорить о дробной, или фрактальной размерности, пространства, которая на всех шагах оставалась одной и той же, как если бы мы разделили квадрат на 9 частей, затем каждый маленький квадрат снова разделили на 9 частей, получив общее число квадратиков, равным 81, и т.д. Такая процедура не влияет на размерность пространства. Число пройденных шагов или показатели степени, в которые возводятся числа k и n, обозначим через m (у нас показано m = 0, 1, 2, 3 и 5). Ломаная Коха, предложенная Гельгом фон Кохом в 1904 г., выступает сейчас в роли фрактала, который прекрасно подходит для моделирования изрезанности береговой линии. Мандельброт в алгоритм построения береговой линии внес элемент случайности, который, однако, не повлиял на основной вывод в отношении длины береговой линии. Поскольку предел
,
длина береговой линии за счет бесконечной изрезанности берега стремится к бесконечности. Процедура сглаживания береговой линии при переходе от более детального масштаба к менее детальному, т.е. согласно рис.4.2 переходы от (д) к (г), от (г) к (в), от (в) к (б), дает одну и ту же величину: на три части длины — одну «бухту», а длина стремится к единичному значению.
В качестве основы можно взять не отрезок единичной длины, а равносторонний треугольник, на каждую сторону которого распространить процедуру умножения изрезанности. В этом случае получим снежинку Коха (рис. 4.3), причем трех видов: вновь образующиеся треугольники направлены только наружу от предыдущего треугольника (а) и (б); только внутрь (в); случайным образом либо наружу, либо внутрь (г) и (д). Сейчас наша ближайшая задача состоит в том, чтобы научиться задавать процедуру построения фрактала Коха.а
б
в
г
д
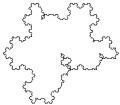
Рис. 4.3
На рис. 4.4 показаны две векторные диаграммы; числа, стоящие над стрелками, видимо, вызовут вопрос: что бы они значили? Вектор 0 совпадает с положительным направлением оси абсцисс, так как его фазовый множитель exp (i2πl/6) при l = 0 сохраняет его направление. Вектор 1 повернут относительно вектора 0 на угол 2π/6, когда l = 1. Вектор 5 имеет фазовый множитель exp (i2π5/6), l = 5. Последний вектор имеет тот же фазовый множитель, что и первый (l = 0). Таким образом, целые числа l характеризуют угол фазового множителя единичного вектора.
Рис. 4.4
Итак, мы рассмотрели первый шаг (рис. 4.4а), который задает рекурсивную процедуру для всех последующих шагов и, в частности, для второго шага (рис. 4.4б). Ставится вопрос, как перейти от набора чисел φ1 = {0 1 5 0} к φ2 = {0 1 5 0 1 2 0 1 5 0 4 5 0 1 5 0}? Ответ: через прямое перемножение матриц, когда каждый элемент одной матрицы умножается на исходную матрицу. Поскольку в данном случае мы имеем дело с одномерным массивом, т.е. матрицы представляют собой векторы, то здесь производится умножение каждого элемента одной матрицы-вектора на все элементы другой матрицы-вектора. Кроме того, элементы матрицы-вектора φ1 состоят из показательных функций exp (i2πl/6), следовательно, при перемножении числа h нужно будет складывать по mod (6), а не умножать. После этих разъяснений становится понятна следующая запись:
φ2 = φ1 × φ1 = {0 1 5 0} × {0 1 5 0} =
= {[(0 1 5 0) + 0] [(0 1 5 0) + 1] [(0 1 5 0) + 5] [(0 1 5 0) + 0]} =
= {[0 1 5 0] [1 2 0 1] [5 0 4 5] [0 1 5 0]} = {0 1 5 0 1 2 0 1 5 0 4 5 0 1 5 0};
φ3 = φ2 × φ1, ..., φm = φm – 1 × φ1.
Итак, для задания фрактала Коха нам требуется три числа и один вектор, а именно: k = 3 — коэффициент подобия; n = 4 — число частей, образующих паттерн; h = 6 — число, определяющее фазовый множитель exp (i2πl/h) и фигурирующее в основании mod (h), по которому производится сложение показателей экспоненты, и базовый вектор или, собственно, сам паттерн φ1 = {0 1 5 0}. Заметим, слово паттерн часто заменяют словосочетанием затравочная схема, структура, матрица или генератор фрактала. Однако вряд ли есть смысл искать другие русские эквиваленты этому английскому слову, уже прочно вошедшему в русский лексикон. Если факт заимствования термина налицо, то и нужно его принимать со всеми теми семантическими оттенками, которые существуют в английском языке. Прямой перевод слова pattern означает пример для подражания, образец, образцовая модель, система, стиль, выкройка, орнамент, узор, рисунок. Невозможно подыскать такой же емкий и точный термин в русском языке, передающий этот же самый смысл.
Приведем еще четыре фрактала и их краткое описание через векторную диаграмму. Читателю не составит большого труда самому придумать сотни аналогичных фракталов. Затем можно заставить компьютер производить прямое перемножение векторов, а результат отображать на экране дисплея, как на рис. 4.5.
Приведем еще четыре фрактала и их краткое описание через векторную диаграмму. Читателю не составит большого труда самому придумать сотни аналогичных фракталов. Затем можно заставить компьютер производить прямое перемножение векторов, а результат отображать на экране дисплея, как на рис. 4.5.
а)
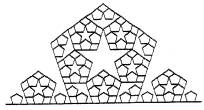
k = 3, n = 8, h = 5, φ = {0 0 1 2 3 4 0 0};
б)
k = 3, n = 8, h = 5, φ = {0 0 2 4 1 3 0 0};
в)

k = 3, n = 5, h = 4, φ = {0 1 0 3 0};
г)

k = 3, n = 7, h = 6, φ = {0 1 5 3 5 1 0}.
Рис. 4.5
Эта необыкновенная легкость, с которой можно получить красивейшие узоры с помощью самой незатейливой математики и элементарного программирования, привлекла к теме фракталов огромное число любителей. Однако все приведенные фракталы одномерные, т.е. их графические изображения представляют собой линии, а в прямом умножении участвуют векторы. А нет ли таких фракталов, когда бы в прямом произведении участвовали полноценные матрицы? Да, есть; на рис. 4.6 в трехмерном пространстве изображена губка Менгера (а), и двумерный эквивалент (б). Она также является фракталом, для которого процедуру рекурсии можно отразить с помощью матриц. Для трехмерной губки пришлось бы иметь дело с трехмерными матрицами — такие существуют, действия с ними хорошо известны, но они слишком громоздки, чтобы использовать их сейчас для анализа. Пусть ими занимаются компьютеры, мы же обратимся к двумерному случаю. Поставим темным участкам квадрата в соответствие 1, а светлым — 0 (рис. 4.6б). В этом случае паттерн плоской губки φ1 с единственной дыркой внутри выглядит в виде матрицы 3 × 3. Перемножая ее прямым образом саму на себя или возводя ее последовательно в степень 2, 3 и т.д., мы получим фракталы φ2, φ3 и т.д. В частности, φ2 = φ1 × φ1 равно прямому произведению двух матриц:
а
б
Рис. 4.6
Фрактальной структуре подчинены коэффициенты бинома:
(1 + x)n = 1 + nx + n(n – 1)x2/2! + n(n – 1)(n – 2)x3/3! + ... + n!xk/(n – k)!k! + ...
Если коэффициенты бинома выстроить рядами, как это показано в табл. 4.1 (в центре), то получим так называемый треугольник Паскаля. Беря все числа в треугольнике Паскаля последовательно по mod (2), mod (3), mod (4), mod (5) и т.д., мы будем получать треугольные матрицы, верхняя часть которых состоит из нулей. Эти треугольные матрицы можно уже перемножать прямым образом. Например, прямое перемножение двух треугольных матриц 3 × 3 по mod (3) дает в результате треугольную матрицу 9 × 9, которая в точности совпадает с треугольником Паскаля, записанным по mod (3) этого же размера: φ2 = φ1 × φ1 равно прямому произведению двух матриц следующего вида:
Таблица 4.1
1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 3 3 1 1 1 1 4 6 4 1 1 1 1 1 1 5 10 10 5 1 1 1 1 1 1 6 15 20 15 6 1 1 1 1 1 1 1 1 1 1 7 21 35 35 21 7 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Такое перемножение справедливо для случая mod (4), mod (5) и т.д. В случае же, когда треугольник Паскаля составляется по mod (2), его внешний вид напоминает губку Менгера, но только треугольной формы (рис. 4.7).
Вообще, губки Менгера треугольной, квадратной, кубической, пирамидальной и любой другой формы приковали к себе внимание ученых потому, что они обладают одним замечательным свойством: чем шире их габаритные границы (рис. 4.6), тем больший внутренний объем в них образуется. Иначе говоря, при разрастании губки отношение ее внешнего объема к внутреннему стремится к единице. Это свойство является самым важным для губок, живых и искусственных, например, тех, которыми мы моемся. За счет множественных внутренних пустот губка способна удерживать большое количество влаги, т.е. она работает в качестве своеобразного сосуда, который состоит не из одной открытой камеры, а из огромного числа соединенных друг с другом полостей. Губку можно рассматривать как древовидную структуру. В природе встречаются такие виды растений и животных, в частности, обитающие в морских глубинах, у которых густые ветви, расположенные ближе к корневому телу, срастаются так, что образуют одну губчатую поверхность, хотя внешние ветви могут сильно вытягиваться в виде усов, щупальцев или палпусов для захвата пищи. Более того, если на биологическое вещество смотреть с точки зрения его структурно-пространственной организации, то окажется, что оно сплошь выстроено по губчатому принципу. Это касается в большей мере, скажем, дыхательной системы, хотя аналогично устроены и системы кровообращения, пищеварения и прочие системы жизнеобеспечения.