Конструктивная математика
Акимов О.Е.
16. Числовые закономерности
От истории перейдем к задачам сегодняшнего дня. Конструктивная идеология прекрасно изложена в книге Джорджа Пойя «Математика и правдоподобные рассуждения». Пойа исследует геометрический вопрос о количестве частей, на которые делится прямая точками, плоскость прямыми и пространство плоскостями [33, с. 67]. Очевидно, что одна точка делит прямую на две части, две точки – на три части, три точки — на четыре части, а n точек – на n + 1 части. Одна прямая делит плоскость на 2 ячейки, две прямых — на 4 ячейки, три прямых — на 7 частей и четыре прямых — на 11 частей. Два последних случая изображены на рис. 10а и рис. 10б. В данном случае установить закономерность числа ячеек плоскости от числа делящих прямых уже сложнее.
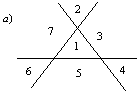
Рис. 10
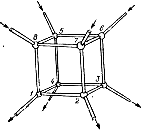
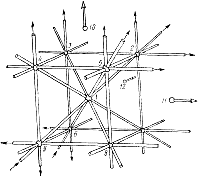
Наконец, исследуем деление пространства плоскостями. Одна плоскость делит пространство на 2 части, две плоскости — на 4 части, три плоскости — на 8 частей и четыре плоскости — на 15 частей. На рис. 11а и рис. 11б изображены фигуры, разбивающие пространство на 8 и 15 ячеек. Плоскости должны иметь продолжение во все стороны. Если это условие не выполняется, система ячеек будет подчиняться другой закономерности. Так, на рис. 11в 16 ограниченных ребрами куба плоскостей делит пространство всего на 7 ячеек. На рис. 12а проведены 9 бесконечных плоскостей, а на рис. 12б плоскости получаются при продолжении 6 граней куба и 6 диагональных плоскостей, проходящих через каждые два противоположных ребра.

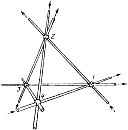
Рис. 11
Возникшая система ячеек называется конфигурацией Рейя, которая рассматривается в рамках проективной геометрии. О конфигурациях рассказывается в другой замечательной книге — Д. Гильберта и С. Кон-Фоссена «Наглядная геометрия» [34, с. 67], откуда и были взяты данные рисунки. Рис. 12 убеждает нас, сколь не проста задача подсчета пространственных ячеек для случая 9 и 12 плоскостей.

Рис. 12
Однако, если все подсчеты последовательно записывать в табл. 6, структура которой напоминает модифицированную структуру таблицы биноминальных коэффициентов (о ней речь пойдет ниже), то можно легко уловить закономерность.
Таблица 6
q0 q1 q2 q3 q4 q5 ... 1 1 1 1 1 1 ... 1 2 2 2 2 2 ... 2 3 4 4 4 4 ... 3 4 7 8 8 8 ... 4 5 11 15 16 16 ... 5 6 16 26 31 32 ... 6 7 22 42 57 63 ... ... ... ... ... ... ... ... В столбце q0 табл. 6 указано число делящих элементов; в столбце q1 указано число частей при делении прямой точками; в столбце q2 — число ячеек при делении плоскости прямыми; в столбце q3 — число областей при делении пространства плоскостями. При этом в табл. 6 обнаруживается любопытная закономерность: каждый элемент таблицы складывается из двух соседних элементов, стоящих на предыдущей строке, например, 11 = 4 + 7, 42 = 16 + 26 и т.д. Поэтому можно легко подсчитать число частей прямой, плоскости и пространства без каких-либо геометрических построений. Табл. 6 можно сравнивать и с таблицей биноминальных коэффициентов. Самым интригующим свойством табл. 6 является то, что она легко может быть продолжена в сторону многомерных пространств: четырех, пяти и т.д. измерений.
Табл. 7 похожа на табл. 6. Взгляните на нее внимательно: суммы элементов строк и столбцов, заканчивающихся на диагонали, образуют квадраты элементов, стоящих на диагонали:
1² = 1,
2² = 1 + 2 + 1,
3² = 1 + 2 + 3 + 2 + 1,
4² = 1 + 2 + 3 + 4 + 3 + 2 + 1,
5² = 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1,
6² = 1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1,
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...Таблица 7
q0 q1 q2 q3 q4 q5 ... 1 1 1 1 1 1 ... 1 2 2 2 2 2 ... 2 2 3 3 3 3 ... 3 2 3 4 4 4 ... 4 2 3 4 5 5 ... 5 2 3 4 5 6 ... 6 2 3 4 5 6 ... ... ... ... ... ... ... ... Данные таблицы прекрасно демонстрируют конструктивный подход, наиважнейшими принципами которого является индукция и аналогия, позволяющие открыть, построить или вычислить общие случаи, выходящие за рамки непосредственных геометрических представлений. Рассмотренные таблицы являются родными сестрами различного рода головоломок, в частности, магических квадратов, которые изображены на рис. 13а. Первый квадрат (3 х 3) по всем горизонтальным, вертикальным и диагональным линиям дает число 15. Этот квадрат был начертан древнекитайским математиком пять тысяч лет назад на черепашьем панцире, найденном в наши дни. Два следующих квадрата (4 х 4) дают сумму 34. Один из таких квадратов изображен на картине Альбрехта Дюрера "Меланхолия" (1514 г.). Сегодня существует компьютерная программа, позволяющая составлять квадраты любой размерности. Вот результат работы этой программы: магический квадрат (5 х 5) дает число 65, квадрат (6 х 6) — 111, квадрат (10 х 10) — 505 и т.д. Каждый из квадратов, кроме первого (3 х 3), имеет несколько модификаций, которые можно получить и вручную путем одновременной перестановки столбцов и строк.
Мартин Гарднер, известный автор занимательных книг по математике и физике, рассказал любопытную историю про Клиффорда Адамса, который 50 лет потратил на составление магического шестиугольника (рис. 13б). Сумма элементов по всем линиям, параллельным сторонам шестиугольника, равна одному и тому числу 38:
15 + 13 + 10 = 15 + 14 + 9 = 15 + 8 + 5 + 7 + 3 = 10 + 12 + 16 = ...
( а ) 
( б ) 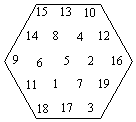 ( в )
( в ) 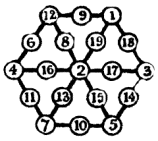 ( г )
( г ) 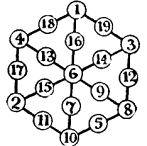
Рис. 13
В книге Генри Дьюдени «200 знаменитых головоломок мира» в задаче № 35 тоже приводится шестиугольник из 19 чисел. Если на рис. 13в сложить три числа от центра по одной из спиц шестиугольника или по его стороне, то получим число 22. Например:
22 = 2 + 19 + 1 = 2 + 17 + 3 = 3 + 14 + 5 = 5 + 10 + 7 = …
А теперь, внимание: если все указанные числа заменить на числа-дополнения к числу 20, то мы получим магический шестиугольник с суммой 38, который, однако, отличается от своего собрата, изображенного на рис. 13б. В частности, приведенное выше равенство будет выглядеть следующим образом:
38 = 18 + 1 + 19 = 18 + 3 + 17 = 17 + 6 + 15 = 15 + 10 + 13 = …
В разъяснениях к задаче № 35 Дьюдени пишет: «Девятнадцать чисел можно расположить таким образом, чтобы сумма вдоль каждой прямой равнялась любому числу от 22 до 38 включительно, кроме 30. В некоторых случаях существует несколько различных решений, но в случае 23 их только два. Я привел один из них (рис. 13г). Чтобы получить другое решение, поменяйте на рис. 13г местами числа 7, 10, 5, 8, 9, 18 соответственно с числами 13, 4, 17, 2, 15, 12, а остальные числа оставьте на прежних местах. В любом случае в центре должно находиться четное число от 2 до 18. Каждое решение имеет дополнительное решение. Таким образом, если вместо каждого числа на приведенном рисунке мы поставим разность между ним и 20, то получим решение для случая 37. Аналогичным образом из расположения на исходном рисунке (рис. 13в) мы сразу же получим решение для случая 38». Иначе говоря, здесь имеет место принцип двойственности относительно числа 20.
Магические квадраты и шестиугольники демонстрируют одинаковые суммы чисел, которые определенным образом расположены в таблицах. Но среди математических игр существуют задачи, связанные с позиционным упорядочением цифр, образующих числа. В книге А.П. Доморяда [35] можно найти равенства:
1 : 2 = (123 – 45) : (67 + 89), 1 = 1 + 23 – 45 – 67 + 89.
Автор приводит дроби, в которых разрешены «забавные сокращения» цифр:
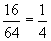 ,
,
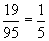 ,
,
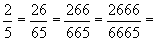 ...,
...,
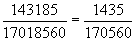 и т.д.
и т.д.
Любопытные действия с числами при возведении их в квадрат нашел Г. Топадзе (табл. 8):
Таблица 8
44²
———
16
1616
16
———
193655²
———
25
2525
25
———
302566²
———
36
3636
36
———
435677²
———
49
4949
49
———
5929... 555²
———
25
2525
252525
2525
25
———
308025666²
———
36
3636
363636
3636
36
———
443556Чтобы понять, как получаются эти квадраты, приведем расшифровку последней операции с «сатанинским числом» 666:
666² = (6 · 111)² = 36 · 12321 =
= 36 · (100 + 1010 + 10101 + 1010 + 100) =
= 3600 + 36360 + 363636 + 36360 3600 = 443556.У этого автора мы находим и такие симметричные равенства:
12 · 42 = 24 · 21
102 · 402 = 204 · 201
1002 · 4002 = 2004 · 2001
10002 · 40002 = 20004 · 20001
. . . . . . . . . . . . . . . . . . . . . . . . . . .Интересными являются те соотношения, в которых наблюдается определенная цифровая симметрия, как, например, здесь:
999999999² = 12 345 678 987 654 321 ·
· (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1).Как составлено это равенство, понять несложно, если помнить, что первый сомножитель образован числом 111111111², а сумма в скобках дает число 9².
М.А. Гершензон, другой известный автор книг по математическим головоломкам, нашел замечательные ряды из числовых равенств:
0 · 9 + 1 = 1
1 · 9 + 2 = 11
12 · 9 + 3 = 111
123 · 9 + 4 = 1111
1234 · 9 + 5 = 11111
12345 · 9 + 6 = 111111
123456 · 9 + 7 = 1111111
1234567 · 9 + 8 = 11111111
12345678 · 9 + 9 = 111111111
1 · 8 + 1 = 9
12 · 8 + 2 = 98
123 · 8 + 3 = 987
1234 · 8 + 4 = 9876
12345 · 8 + 5 = 98765
123456 · 8 + 6 = 987654
1234567 · 8 + 7 = 9876543
12345678 · 8 + 8 = 98765432
123456789 · 8 + 9 = 987654321
9 · 9 + 7 = 88
98 · 8 + 6 = 888
987 · 8 + 5 = 8888
9876 · 8 + 4 = 88888
98765 · 8 + 3 = 888888
987654 · 8 + 2 = 8888888
9876543 · 8 + 1 = 88888888
98765432 · 8 + 0 = 888888888
987654321 · 8 + 1 = 8888888888
111 111 111 = 123456789 · 09
222 222 222 = 123456789 · 18
333 333 333 = 123456789 · 27
444 444 444 = 123456789 · 36
555 555 555 = 123456789 · 45
666 666 666 = 123456789 · 54
777 777 777 = 123456789 · 63
888 888 888 = 123456789 · 72
999 999 999 = 123456789 · 81
Глядя на них, формалист скажет, что эти задачи не касаются никаких геометрических образов и что мы имеем дело только с арифметикой и символами. Тем не менее данные ряды являются прекрасной средством для оформления конструктивных задач комбинаторного типа, где проявляются какие-либо регулярности. Вначале всякого исследования зрительный образ играет решающую роль; именно он диктует логику моделирования всей ситуации. При нарушении конструктивной психической функции, когда у человека выключен индуктивный поиск по аналогии, тогда никакие графические образы не помогут.
Вот еще любопытные цифровые последовательности, которые получаются, когда в знаменателе оказываются некоторые простые числа:
01/7 = 0,142857142857142857…
03/7 = 0,428571428571428571…
02/7 = 0,285714285714285714…
06/7 = 0,857142857142857142…
04/7 = 0,571428571428571428…
05/7 = 0,714285714285714285…
08/7 = 1,142857142857142857…
10/7 = 1,428571428571428571…
09/7 = 1,285714285714285714…
13/7 = 1,857142857142857142…
11/7 = 1,571428571428571428…
12/7 = 1,714285714285714285…
15/7 = 2,142857142857142857…
... ... ... ... ...
01/17 = 0,058823529411764705…
10/17 = 0,588235294117647058…
15/17 = 0,882352941176470588…
14/17 = 0,823529411764705882…
04/17 = 0,235294117647058823…
06/17 = 0,352941176470588235…
09/17 = 0,529411764705882352…
05/17 = 0,294117647058823529…
16/17 = 0,941176470588235294…
07/17 = 0,411764705882352941…
02/17 = 0,117647058823529411…
03/17 = 0,176470588235294117…
13/17 = 0,764705882352941176…
11/17 = 0,647058823529411764…
08/17 = 0,470588235294117647…
12/17 = 0,705882352941176470…
18/17 = 1,058823529411764705…
... ... ... ... ... ... ...Аналогичные цифровые «колеса» получаются при простых числах 19, 23, 29 и т.д.
Вообще, нет ничего более загадочного, чем бесконечный ряд простых чисел. Сколько тысяч, а может быть, и миллионов людей думало над универсальной формулой для получения любого наперед заданного простого числа. В таблице 9 приведены множество формул, которые дают простые числа при указанных значениях переменной x. Для проверки работоспособности формул, приводится табл. 10 простых чисел от 2 до 3000.
Таблица 9
| 10x² + 19 | 0 ≤ x ≤ 18 | x³ – x + 7 | – 1 ≤ x ≤ 5 | 2x + 3 | 1 ≤ x ≤ 4 |
| 10x² + 13 | 0 ≤ x ≤ 12 | x³ – x + 13 | – 1 ≤ x ≤ 4 | 2x + 15 | 1 ≤ x ≤ 6 |
| 10x² + 7 | 0 ≤ x ≤ 6 | x³ – x + 23 | – 1 ≤ x ≤ 4 | 3 · 2x + 5 | 1 ≤ x ≤ 8 |
| 10x² + 73 | 0 ≤ x ≤ 4 | x³ – x + 37 | – 1 ≤ x ≤ 5 | 5 · 2x + 3 | 1 ≤ x ≤ 5 |
| 4x² + 37 | 0 ≤ x ≤ 8 | x³ – 7x + 23 | – 3 ≤ x ≤ 8 | 3x + 2 | 0 ≤ x ≤ 4 |
| 4²x² + 37 | 0 ≤ x ≤ 4 | x³ – 7x + 103 | – 5 ≤ x ≤ 7 | 3x + 4 | 0 ≤ x ≤ 3 |
| 8x² + 11 | 0 ≤ x ≤ 5 | x³ – 7x + 353 | – 7 ≤ x ≤ 5 | 3x + 10 | 0 ≤ x ≤ 3 |
| 10x4 + 19 | 0 ≤ x ≤ 7 | x³ – 7x + 373 | – 7 ≤ x ≤ 6 | 5 · 3x + 14 | 0 ≤ x ≤ 7 |
| 10x6 + 19 | 0 ≤ x ≤ 3 | x³ – 13x + 29 | – 4 ≤ x ≤ 7 | 15 · 3x + 14 | 0 ≤ x ≤ 6 |
| 10x8 + 19 | 0 ≤ x ≤ 5 | x³ – 43x + 149 | – 7 ≤ x ≤ 10 | 15 · 3x + 16 | 0 ≤ x ≤ 4 |
Таблица 10
| 2 | 193 | 449 | 733 | 1031 | 1321 | 1637 | 1997 | 2333 | 2677 |
| 3 | 197 | 457 | 739 | 1033 | 1327 | 1657 | 1999 | 2339 | 2683 |
| 5 | 199 | 461 | 743 | 1039 | 1361 | 1663 | 2003 | 2341 | 2687 |
| 7 | 211 | 463 | 751 | 1049 | 1367 | 1667 | 2011 | 2347 | 2689 |
| 11 | 223 | 467 | 757 | 1051 | 1373 | 1669 | 2017 | 2351 | 2693 |
| 13 | 227 | 479 | 761 | 1061 | 1381 | 1693 | 2027 | 2357 | 2699 |
| 17 | 229 | 487 | 769 | 1063 | 1399 | 1697 | 2029 | 2371 | 2707 |
| 19 | 233 | 491 | 773 | 1069 | 1409 | 1699 | 2039 | 2377 | 2711 |
| 23 | 239 | 499 | 787 | 1087 | 1423 | 1709 | 2053 | 2381 | 2713 |
| 29 | 241 | 603 | 797 | 1091 | 1427 | 1721 | 2063 | 2383 | 2719 |
| 31 | 251 | 509 | 809 | 1093 | 1429 | 1723 | 2069 | 2389 | 2729 |
| 37 | 257 | 521 | 811 | 1097 | 1433 | 1733 | 2081 | 2393 | 2731 |
| 41 | 263 | 523 | 821 | 1103 | 1439 | 1741 | 2083 | 2399 | 2741 |
| 43 | 269 | 541 | 823 | 1109 | 1447 | 1747 | 2087 | 2411 | 2749 |
| 47 | 271 | 547 | 827 | 1117 | 1451 | 1753 | 2089 | 2417 | 2753 |
| 53 | 277 | 557 | 829 | 1123 | 1453 | 1759 | 2099 | 2423 | 2767 |
| 59 | 281 | 563 | 839 | 1129 | 1459 | 1777 | 2111 | 2437 | 2777 |
| 61 | 283 | 569 | 853 | 1151 | 1471 | 1783 | 2113 | 2441 | 2789 |
| 67 | 293 | 571 | 857 | 1153 | 1481 | 1787 | 2129 | 2447 | 2791 |
| 71 | 307 | 577 | 859 | 1163 | 1483 | 1789 | 2131 | 2459 | 2797 |
| 73 | 311 | 587 | 863 | 1171 | 1487 | 1801 | 2137 | 2467 | 2801 |
| 79 | 313 | 593 | 877 | 1181 | 1489 | 1811 | 2141 | 2473 | 2803 |
| 83 | 317 | 599 | 881 | 1187 | 1493 | 1823 | 2143 | 2477 | 2819 |
| 89 | 331 | 601 | 883 | 1193 | 1499 | 1831 | 2153 | 2503 | 2833 |
| 97 | 337 | 607 | 887 | 1201 | 1511 | 1847 | 2161 | 2521 | 2837 |
| 101 | 347 | 613 | 907 | 1213 | 1523 | 1861 | 2179 | 2531 | 2843 |
| 103 | 349 | 617 | 911 | 1217 | 1531 | 1867 | 2203 | 2539 | 2851 |
| 107 | 353 | 619 | 919 | 1223 | 1543 | 1871 | 2207 | 2543 | 2857 |
| 109 | 359 | 631 | 929 | 1229 | 1549 | 1873 | 2213 | 2549 | 2861 |
| 113 | 367 | 641 | 937 | 1231 | 1553 | 1877 | 2221 | 2551 | 2879 |
| 127 | 373 | 643 | 941 | 1237 | 1559 | 1879 | 2237 | 2557 | 2887 |
| 131 | 379 | 647 | 947 | 1249 | 1567 | 1889 | 2239 | 2579 | 2897 |
| 137 | 383 | 653 | 953 | 1259 | 1571 | 1901 | 2243 | 2591 | 2903 |
| 139 | 389 | 659 | 967 | 1277 | 1579 | 1907 | 2251 | 2593 | 2909 |
| 149 | 397 | 661 | 971 | 1279 | 1583 | 1913 | 2267 | 2609 | 2917 |
| 151 | 401 | 673 | 977 | 1283 | 1597 | 1931 | 2269 | 2617 | 2927 |
| 157 | 409 | 677 | 983 | 1289 | 1601 | 1933 | 2273 | 2621 | 2939 |
| 163 | 419 | 683 | 991 | 1291 | 1607 | 1949 | 2281 | 2633 | 2953 |
| 167 | 421 | 691 | 997 | 1297 | 1609 | 1951 | 2287 | 2647 | 2957 |
| 173 | 431 | 701 | 1009 | 1301 | 1613 | 1973 | 2293 | 2657 | 2963 |
| 179 | 433 | 709 | 1013 | 1303 | 1619 | 1979 | 2297 | 2659 | 2969 |
| 181 | 439 | 719 | 1019 | 1307 | 1621 | 1987 | 2309 | 2663 | 2971 |
| 191 | 443 | 727 | 1021 | 1319 | 1627 | 1993 | 2311 | 2671 | 2999 |
Эйлер бился над проблемой простых чисел в течение всей своей жизни. Он предложил три замечательных формулы:
p = 2x² + 29, p = x² + x + 41, p = x² – 79x + 1601.
Первая формула действует в диапазоне 0 ≤ x ≤ 28, вторая — 0 ≤ x ≤ 39 и третья — 0 ≤ x ≤ 79, причем второй многочлен в диапазоне 0 ≤ x ≤ 1000 дает 581 простое число, а в диапазоне 0 ≤ x ≤ 11000 — уже 4506 простых чисел.
Эйлер обратил внимание, что квадратичная форма вида x² + ny² продуцирует множество простых чисел (правда, есть и «осечки»), если переменным x и y придавать различные значения из натурального ряда, а n брать из следующего массива чисел:
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 15, 16, 18, 21, 22, 24, 25, 28, 30, ... };
3² + 2² = 13, 3² + 2 · 2² = 17, 3² + 37 · 2² = 157, 10² + 37 · 1² = 137.
В теории простых чисел существует масса теорем, которые доказываются формально-логическим способом. Первым в этом ряду доказательств является теорема Евклида о бесконечном числе простых чисел. Евклид рассуждал так. Пусть число простых чисел будет конечным и p является максимальным из них. Тогда число n = 2 · 3 · 4 · … · p + 1 является не простым и оно делится на какое-то простое число из ряда простых чисел от 2 до p. Но n не может делиться ни на одно из указанного ряда, поскольку остаток от деления окажется равным 1.
Отсюда вытекает, что на любом числовом отрезке [n; n! +1], где n! = 1 · 2 · 3 · 4 · … · n, имеется хотя бы одно простое число. Таким образом, числа:
2, 2! + 1, (2! + 1)! + 1, ((2! + 1)! + 1)! + 1, …
разбивают всю числовую ось на бесконечное число отрезков, в каждом из которых находится по крайней мере по одному простому числу.
Обратите внимание, что теорема Евклида указывает на существование простого числа, но отнюдь не на ближайшее. Факториал растет быстро, так что выписанный выше ряд дает и быстро увеличивающиеся отрезки:
[2; 3], [3; 7], [7; 5041], [5041; » 2,2832e+16477], …
Между тем можно строго логически доказать, что на отрезках вида:
[2; 4], [4; 8], [8; 16], [16; 32], [32; 64], …
имеется не менее одного простого числа. Этот и предыдущий ряды порождены типичными теоремами на существование. Они говорят нам лишь о присутствии простых чисел, но не указывают, какие именно и сколько их.
Выше были выписаны три замечательных многочлена Эйлера, которые дают на больших числовых отрезках только простые числа. Однако можно логическими средствами доказать, что не существует ни одного многочлена от одной переменной, который бы давал только простые числа.
Теперь взгляните на табл. 11 и табл. 12, где приведены последовательности простых чисел (по материалам [36]). Как и упорядоченные ряды равенств, приведенные выше, они дают человеку надежду на открытие какой-то регулярности в мире простых чисел.
Таблица 11
19 131 449 991 1003001 1880881 199 13331 44449 99991 1008001 1881881 1999 1333331 444449 9999991 1114111 1883881 19999 1777 499 11311 1117111 1884881 19 7177 4999 13331 1212121 1908091 109 7717 49999 15551 1221221 1909091 1009 3373 47777 16661 1300031 3001003 10009 3733 77477 19991 1333331 3002003 31 7333 77747 72227 1444441 3007003 331 59 23 75557 1551551 3222223 3331 599 233 76667 1556551 3337333 33331 59999 2333 78887 1557551 7666667 333331 599999 23333 79997 1600061 9888889 Таблица 12
19 103 409 145701 197 1039 4099 1457011 1979 10399 40993 14570117 19793 103997 409933 145701173 197933 1039979 4099339 1457011739 1979339 10399793 40993391 14570117399 19793393 103997939 409933919 145701173999 197933933 1039979399 4099339193 1457011739993 1979339333 10399793993 40993391939 14570117399939 — 103997939939 409933919393 145701173999399 — — 4099339193933 1457011739993993 — — — 14570117399939939 — — — 145701173999399393 Математическая эстетика этих таблиц зависит от системы счисления: в десятичной (Dec) системе счисления будут обнаруживаться одни закономерности, в шестнадцатеричной (Hex) — другие, в восьмеричной (Oct) — третьи, а в бинарной (Bin) — четвертые. В первом столбце табл. 12а воспроизведена часть первого столбца табл. 12. В последующих столбцах воспроизведены числа первого столбца, только выражены они в Hex, Oct и Bin системах счисления. Главное здесь то, что закономерности, обнаруженные в Dec системе исчисления, существуют также в Hex, Oct и Bin системах. И можно не сомневаться, что пока жив человек, он будет пытаться найти их.
Таблица 12а
Dec Hex Oct Bin 19 13 23 10011 197 C5 305 11000101 1979 7BB 3673 11110111011 19793 4D51 46521 100110101010001 197933 3052D 602455 110000010100101101 1979339 1E33CB 7431713 111100011001111001011 Простые числа — это самая большая загадка природы. Слово «природа» использовано здесь по своему прямому назначению; математика действительно является квинтэссенцией физики. Когда люди удивляются, отчего это физические явления так хорошо описываются математическими формулами, они не догадываются, что математика — это часть физики, только наиболее рафинированная ее часть. Натуральный ряд чисел, отрицательные и комплексные числа, прямые линии и различные кривые, пространственные фигуры, векторы и тензоры, алгебраические, тригонометрические и дифференциальные уравнения — все это возникло не у нас в голове, а пришло к нам из окружающего мира. Поэтому история математики тесно переплетена с историей физики, и наоборот.
Действия с комплексными числами соответствуют операциям с векторами на плоскости, а им, в свою очередь, можно поставить в соответствие токи и напряжения, установившиеся в электрической цепи с конденсаторами и катушками индуктивности. Говорят, токи и напряжения электрической цепи моделируются векторами на плоскости, но можно сказать иначе: векторы на плоскости моделируются токами и напряжениями электрической цепи. Все зависит от того, с чем человек больше знаком: если он одинаково не знает ни электротехники, ни векторного анализа, то моделирование одного неизвестного объекта другим ни к чему хорошему не приведет. Однако геометрическое моделирование имеет определенное преимущество перед моделированием токами и напряжением — оно наглядно. Формула умножения двух комплексных чисел и действия с токами и напряжениями приобретают более глубокое содержание, если их продемонстрировать с помощью поворотов векторов.
Некоторые разделы физики, такие как оптика, небесная механика, механика сплошных сред, термодинамика, электродинамика, кристаллография, неразрывно связаны с соответствующими математическими разделами: евклидовой геометрией, сферической тригонометрией, тензорным анализом, теорией дифференциальных уравнений, векторной алгеброй и т.д. Простые числа играют исключительно важную роль в теории групп, а группы описывают симметрию кристаллических минералов. Они также применяются в атомной физике или физике элементарных частиц. Разве можно после этого утверждать, что простые числа и теория групп являются выдумкой математиков. Разумеется, нет; математик изучил свойства этих чисел, определил понятия, ввел термины и символы. С помощью логики он сам для себя доказал, что в его математических представлениях отсутствуют противоречия, хотя правильно выбранная математическая модель сама диктует логически верные соотношения. Но сущность всех математических формул и уравнений независимо от воли математика существовала в природе.
Поэтому мы и говорим, что таблица простых чисел представляет собой точно такое же естество, как например, периодическая таблица химических элементов или перечень биологических видов. Закон Ома I = U/R или закон Ньютона F = a · m ничем принципиальным не отличаются от формулы Эйлера для простых чисел p = 2x² + 29, которая работает, однако, при 29 значениях x. Почему существуют область действия закона? Да потому что всякая модель, теория, уравнение или формула есть только крохотная часть природы. Если кому-то показалось, что он нашел глобальную модель, универсальную теорию или всеобщую формулу, то это только говорит об узости его кругозора. Конструктивист не стремится к глобальности, универсализму и всеобщности; для него не существует «оснований», он всегда начинает исследовать предмет как бы с середины. Как раз невежды любят предлагать универсальные рецепты на все случаи жизни, мудрые же рады малому: формула описывает тридцать простых чисел – хорошо, сорок — превосходно, восемьдесят — счастье. В табл. 9 приведены элементарные формулы, описывающие 4, 5, 6, 7, ... простых чисел. Тем, кто любит рассуждать о «фундаментальных проблемах» природы, мы рекомендуем самим составить формулу, которая для начала описывала хотя бы три простых числа.