Конструктивная математика

Акимов О.Е.

27. Структурный фактор

Зонные структуры Si и Ge, изображенные на рис. 31, вычерчены в обратном пространстве кристалла. Кое-что о k-пространстве было сказано, но этого явно недостаточно для отчетливого понимания закона дисперсии E(k). Существует несколько десятков пространственных конфигураций атомов: как выглядят их решетки, как найти обратные им, как применить теорию групп для их расчета, как учесть структурный фактор в гамильтониане? Ведь мы не касались вопросов составления ЛКАО-матрицы и не знаем, почему, собственно, ряд матричных элементов в ней равны нулю; есть параметры E_xx и E_xy, но почему-то отсутствуют E_zz, E_yy, E_xz и E_yz. Видимо, это как-то связано с симметрией электронных оболочек и устройством кристаллической решетки, но как? 

Не все мы сможем рассказать, поскольку наша цель состоит не в том, чтобы всесторонне осветить задачи физики полупроводников, а в том, чтобы в выгодном свете представить теорию групп, обслуживающую эту самую физику полупроводников. Конечно, мы постараемся приложить максимум усилий для того, чтобы физическая сторона рассматриваемых явлений была понятна читателю, однако главная задача состоит в том, чтобы убедительно продемонстрировать эффективность конструктивной математики, к которой, в частности, принадлежит и теория групп. Будущие специалисты по материалам полупроводниковой техники для уяснения каких-то непонятных им вопросов материаловедения должны будут, очевидно, обратиться все же к литературе, ограниченный список которой приведен и в конце нашего учебника. Итак, обратное пространство кристалла, что это такое и как его найти.

Если узлы прямой решетки определить равенством 

R_i = n₁a₁ + n₂a₂ + n₃a₃, 

то узлы обратной решетки определятся равенством 

K_i = m₁b₁ + m₂b₂ + m₃b₃, 

причем базисные векторы обоих пространств ортогональны и нормированы. Последнее означает, что выполняется условие: 

a_ib_j = 2πδ_ij     или     exp(iKR) = 1. 

Из последних равенств немедленно вытекает связь между базисными векторами прямого и обратного пространства:

, , .

На рис. 32 показаны 14 пространственных решеток Браве; кубические — простая (P), объемоцентрированная (I) и гранецентрированная (F) для специалистов по материалам полупроводниковой техники являются особенно важными. Прямыми вычислениями можно убедиться, что обратная решетка для простой кубической (ПК) есть также ПК решетка; объемоцентрированной кубической решетке (ОЦК) отвечает гранецентрированная решетка (ГЦК), и наоборот; наконец, для гексагональной плотноупакованной решетки (ГПУ) обратной является опять же ГПУ.

Рис. 32

К примеру, ГЦК — решетка определяется следующими тремя векторами:

a₁ = a(0, ½, ½),   a₂ = a(½, 0, ½),   a₃ = a(½, ½, 0). 

Найдем по предыдущим формулам вектора обратной решетки, для чего сначала определим произведения векторов, стоящие в числителе и знаменателе дробей:

, 

;

отсюда

 ,     ,    

— три вектора определяют узлы ОЦК ячейки.

Процедуру вычисления векторов обратной решетки можно упростить, если прибегнуть к матрицам. Пусть координаты прямой ГЦК решетки a_i будут записаны элементами матрицы A, тогда обратная матрица A^–1 = B укажет на координаты обратной ОЦК решетки b_i:

,     .

К понятию обратной решетки можно прийти и другим путем. Если рассмотреть разложение какой-либо одномерной периодической функции f (r) = f (r + R), где R — пространственный период прямого пространства, в ряд Фурье:

f (r) = Σ_K S(K) exp(iKR) = Σ_K S(K) exp [iK(r + R)] = f (r + R),

то здесь появляется структурный фактор S(K), для которого K есть радиус-вектор, пробегающий узлы обратной решетки. Так как exp (iKR) = 1, структурный фактор найдется через интеграл:

,

где Ω — объем элементарной ячейки прямой решетки, по которой и производится интегрирование. Поскольку обратная решетка определяется через коэффициенты преобразования Фурье, то k-пространство часто называют Фурье-пространством. Если в элементарной ячейке содержится N атомов с координатами ai, то распределение атомов в ней можно описать через δ-функцию:

f (r) = Σ_R,i δ(k – R – a_i).

В пределах элементарной ячейки R = 0, следовательно, суммирование производится только по атомам с координатами a_i, а структурный фактор сводится не к интегралу, а к простой сумме:

.

Для ГЦК с координатами

a₀ = a(0, 0, 0),     a₁ = a(0, ½, ½),   

a₂ = a(½, 0, ½),    a₃ = a(½, ½, 0). 

структурный фактор приобретает следующий конкретный вид:

= 

= {1 + exp[– iπ(n₁ + n₂)] + exp[– iπ(n₃ + n₂)] + 

+ exp[– iπ(n₁ + n₃)]}/4 =

= [1 + cos π(n₁ + n₂) + cos π(n₃ + n₂) + cos π(n₁ + n₃)]/4.

Наиболее важные полупроводники, кремний и германий, имеют решетку алмаза, в которой присутствуют еще четыре атома с координатами:

a₄ = a(¼, ¼, ¼),     a₅ = a(¼, ¾, ¾), 

a₆ = a(¾, ¼, ¾),     a₇ = a(¾, ¾, ¼).

Если начало координат выбрано не на атоме, а посередине между двумя атомами, то можно показать, что структурный фактор алмаза связан со структурным фактором ГЦК решетки по формуле:

S_с = cos π/4(n₁ + n₂ + n₃) S_ГЦК.

Большая группа полупроводников, составленных из атомов III и V группы, II и VI группы Периодической таблицы Менделеева, например: GaAs, GaP, GaSb, InAs, InP и т.д., имеют решетку цинковой обманки (ZnS). Пространственная решетка ZnS, куда входят уже два рода атомов, теряет центр симметрии и структурный фактор становится антисимметричным:

S_ЦО = exp [iπ/4(n₁ + n₂ + n₃)] S_ГЦК.

Рис. 33

На рис. 33 показаны элементарные ячейки: а) Cu, б) W, в) Mg, г) алмаза, д) NaCl, е) CsCl, ж) ZnS, з) ZnO, и) NiAs, к) CaF, л) CuAu, м) Cu3Au. Для каждой из них, в соответствии со структурным фактором, можно построить элементарные ячейки обратной решетки. Важно уметь строить одну-единственную элементарную ячейку, поскольку закон дисперсии E_n(k) приводится только для нее одной, и здесь на первый план выдвигается понятие зоны Бриллюэна (ЗБ). Первую ЗБ определяют как область в обратном пространстве, окружающую один из узлов обратной решетки и ограниченную набором плоскостей, проходящих через середины векторов, соединяющих в обратной решетке данную точку с ее ближайшими соседями.

Рис. 34

На рис. 34 показана первая ЗБ для двумерной косоугольной решетки; на рис. 35 вычерчены уже десять ЗБ для двумерной квадратной решетки. Точно таким же половинным делением расстояния между двумя узлами определяется ЗБ в трехмерном пространстве. На рис. 36а приведены базисные векторы ОЦК решетки, а на рис. 36б — первая ЗБ, имеющая форму правильного ромбододекаэдра. На рис. 37 приведены первых четыре ЗБ для ГЦК решетки. На рис. 38 указаны симметричные точки (Г, L, Λ, Δ, …) первой ЗБ для ГЦК решетки, представляющая собой полуправильный многогранник Архимеда — усеченный октаэдр. Симметричные точки можно видеть на энергетических зонах, рассчитанных ЛКАО-методом (рис. 31а).

Рис. 35

Рис. 36

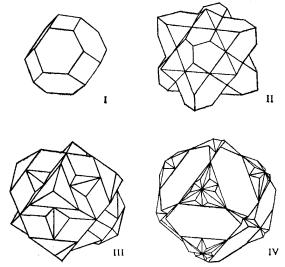
Рис. 37

Рис. 38

Рис. 39

На рис. 39 вычерчены ЗБ для всех 14 решеток Браве, показанные в прямом пространстве на рис. 32. Соответствия между ЗБ и решетками Браве следующие: а) триклинная, б) моноклинная Р, в) моноклинная С, г) ромбическая Р, д) ромбическая С, е) ромбическая I, ж) ромбическая F, з) тетрагональная Р', и) тетрагональная I, к) тригональная R, л) гексагональная Р, м) кубическая Р, н) кубическая F, о) кубическая I. Поскольку выбор ячеек может быть осуществлен несколькими способами, то существует и несколько вариантов ЗБ; поэтому для 14 решеток Браве вычерчено 22 ЗБ.