Конструктивная математика

Акимов О.Е.

26. Закон дисперсии по методу ЛКАО

Даже в очень приблизительной модели химической связи, представленной на рис. 30, можно говорить о зонном строении энергетических уровней, которая существует в реальных полупроводниках. Запрещенной зоной здесь является разность энергий

E_g = E(σ*) – E(π); 

валентная зона с уровнями, заполненными электронами, здесь определяется как 

E_v = E(π*) – E(σ);

наконец, зона проводимости, свободная от электронов, но, в случае возбуждения, электроны проводимости приобретают два указанных в разности значения энергии: 

E_c = E(π*) – E(σ*).

Симметрия энергетических уровней в этой простейшей модели пока никак не проявляет себя, поскольку здесь ничего не говорится о структурном факторе; да и само k-пространство пока отсутствует. Но все же о степени вырождения энергетических уровней здесь говорить можно. Верхний валентный уровень трехкратно вырожден и симметричен; его симметрия в двух различных системах обозначения равна

E(π) = E(Г'₂₅) = E(F_2g).

Нижний валентный уровень однократно вырожден и тоже симметричен:

E(σ) = E(Г₁) = E(A_1g).

Два уровня проводимости антисимметричны, нижний однократно вырожден, верхний — трехкратно; их обозначения в теории групп следующие: 

E(σ*) = E(Г'₂) = E(A_1u),  E(π*) = E(Г₁₅) = E(F_1u).

Ставится задача поиска конкретных значений четырех энергий E(Г'₂₅), E(Г₁), E(Г'₂) и E(Г₁₅) в k-пространстве по известным из эксперимента значениям энергии электронов для свободных атомов a и b: , , и , ориентируясь на минимум энергии для молекулярных орбиталей (МО). При этом волновая функция МО получается как линейная комбинация атомных орбиталей (ЛКАО). 

Для решения этой задачи обратимся к основному уравнению атомной физики — уравнению Шредингера, которое запишем в самом общем виде: Hψ = Eψ, где H — гамильтониан, конкретный вид которого нам нужно установить, ψ — волновая функция МО и E — искомая энергия системы. Чтобы найти энергию, нам необходимо умножить уравнение Шредингера слева на сопряженную волновую функцию и проинтегрировать по пространству, где локализована функция ψ, получим

.

Энергия E — скалярная величина, поэтому

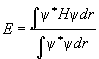
Рассмотрим простейший случай. Пусть волновая функция молекулярной орбитали есть линейная комбинация только двух атомных волновых функций, т.е. имеем ψ = c₁c₁ + c₂c₂. Подставляем ее в уравнение энергии, получим

=

= ,

где

,   ,

;

,   ,

.

Как было сказано, физическая система стремится занять такое состояние, которое отвечало бы минимуму энергии. Условием минимума энергии E является , . Найдем первую производную от E по c₁:

= ×

× [ –

– ].

Используя первое из условий минимизации, получим

.

что эквивалентно уравнению 

c₁(H₁₁ – ES₁₁) + c₂(H₁₂ – ES₁₂) = 0.

Аналогичным образом находим уравнение в соответствии со вторым условием: 

c₁(H₁₂ – ES₁₂) + c₂(H₂₂ – ES₂₂) = 0. 

Разрешенные значения энергии будут соответствовать корням детерминанта:

.

В наших силах функции атомных орбиталей ортонормировать:

(δ_ij = 1 при i = j, δ_ij = 0 при i ≠ j).

Тогда значения энергии находятся элементарно:

, 

.

Если линейная комбинация молекулярной орбитали образована из n атомных орбиталей, то собственные значения энергии будут находиться путем диагонализации матрицы гамильтониана размерностью n × n. Диагональные матричные элементы гамильтониана — это значения энергий электронных уровней в свободном атоме, т.е. когда нет никакого взаимодействия с соседними атомами. Если снова взять самый элементарный случай, то диагональными элементами будут значения H₁₁ = и H₂₂ = . Для полного расчета взаимодействия двух сближенных атомов a и b необходимо иметь матрицу гамильтониана размерностью 8 × 8, чтобы учесть также значения энергии от шести p-состояний. Самая большая проблема состоит в нахождении конкретного вида недиагональных элементов матрицы гамильтониана H_ij. Прежде чем приступить к ее решению, нам нужно ввести понятие функции Блоха.

В кристаллической решетке электрон не находится в центрально-симметричном поле одного ядра с зарядом Ze, рассматривая энергетические уровни электрона, свободного водородоподобного атома. На него действует периодический потенциал от всей решетки в форме: V(r) = V(r + R), где R — постоянная решетки. На каждый электрон в отдельности будет влиять кулоновское поле от всех остальных электронов. Однако их действие можно включить в периодический потенциал ядерного остова кристаллической решетки. В этом случае говорят об одноэлектронном или одночастичном приближении. В таком периодическом потенциале волновая функция электрона ψ по-прежнему будет представлять собой плоскую волну, но, согласно теореме Блоха, ее амплитуда A окажется промодулированной периодическим потенциалом решетки, т.е.

ψ(r + R) = A(r + R)exp[ik(r + R)] =

= A(r) exp(ikr) exp(ikR) = ψ(r)exp(ikR).

Таким образом, любая волновая функция, будь она плоской (для свободного электрона ЗП) или сферической волной (для связанного электрона ЗВ), приобретает важный фазовый множитель в виде экспоненты exp(ikR).

Матричные элементы, в которых в качестве атомных функций использовались сферические гармоники Y(θ, φ), были вычислены в 1954 году Слэтером и Костером. Приведем результаты их вычислений интегралов перекрытия для атомных s- и p-орбиталей (здесь V — объемы перекрытий, l = – — направляющий косинус):

E_ss = V_ssσ,     E_sp = lV_spσ, 

E_xx = l²V_ppσ + (1 – l²)V_ppπ,

E_xy = l²V_ppσ – l²V_ppπ.

В решетке цинковой обманки каждый анион (атом a) имеет четыре соседа — катиона (атом b) с координатами вершин тетраэдра:

d₁ = τ(1, 1, 1),     d₂ = τ(1, –1, –1), 

d₃ = τ(–1, 1, –1),     d₄ = τ(–1, –1, 1),

В результате первый недиагональный матричный элемент приобретет вид: = E_ssg₀, где

g₀ = exp iτ (k_x + k_y + k_z) + exp iτ (k_x – k_y – k_z) +

exp iτ (–k_x + k_y – k_z) + exp iτ (–k_x – k_y + k_z)].

Воспользуемся формулами тригонометрии: 

exp iφ = cos φ + i sin φ,

4cos φ₁ cos φ₂ cos φ₃ = 

cos (φ₁ + φ₂ + φ₃) + cos (φ₁ – φ₂ – φ₃) +

+ cos (–φ₁ + φ₂ – φ₃) + cos (–φ₁ – φ₂ + φ₃)

и аналогичной формулой для синусов. Окончательно находим фазовый множитель 

g₀ = cos φ₁ cos φ₂ cos φ₃ – i sin φ₁ sin φ₂ sin φ₃, 

где φ₁ = πk_x/2,     φ₂ = πk_y/2,     φ₃ = πk_z/2; 

координаты волнового вектора можно менять в пределах 0 < k_i < 1 (i = x, y, z), а множитель 4 включен в интеграл перекрытия E_ss. Можно показать, что , где звездочка означает комплексную сопряженность. Остальные фазовые множители равны:

g₁ = – cos φ₁ sin φ₂ sin φ₃ + i sin φ₁ cos φ₂ cos φ₃,

g₂ = – sin φ₁ cos φ₂ sin φ₃ – i cos φ₁ sin φ₂ cos φ₃,

g₃ = – sin φ₁ sin φ₂ cos φ₃ – i cos φ₁ cos φ₂ sin φ₃.

В итоге, матрица ЛКАО-гамильтониана имеет вид табл. 27

Таблица 27

		0	0	0
		–	–	–	0	0	0
0	–		0	0
0	–	0		0
0	–	0	0
	0					0	0
	0				0		0
	0				0	0

Чади и Коэн в 1975 г. вычислили матричные параметры по формулам Слэтера и Костера для нескольких полупроводников, причем число параметров для полупроводников со структурой цинковой обманки равнялось девяти, а со структурой алмаза — шести. Позже Харрисон [49] получил зонные структуры, аналогичные структурам Чади и Коэна, но число параметров сократил до трех на каждый сорт атома. Он также модифицировал метод ЛКАО таким образом, что теперь с его помощью можно рассчитать закон дисперсии E(k) почти для всех элементов Периодической таблицы.

Он предложил конфигурационные перекрытия искать по универсальной формуле V_ijk = η_ijkћ/md², где d — расстояние в ангстремах между ближайшими атомами: для алмаза d = 1.54, далее по рядам: для ряда кремния d = 2.35, для ряда германия d = 2.44, для ряда олова d = 2.80. Расстояние между атомами, стоящими в разных рядах, ищется как среднеарифметическое, например, для CdS расстояние равно d = (2.80 + 2.35)/2 = 2.57 Å. Константа ћ/m = 7,62 эВ × Å. Он также предложил, параметры и считать за один параметр . По вычислениям Харрисона параметры η_ijk имеют следующие числовые значения:

η_ssσ = –1.40,  η_spσ = 1.84,η_ppσ = 3.24, V_ppπ = – 0.81, 

что позволяет рассчитать все параметры E_ss, E_sp, E_xx и E_xy. В табл. 28 приведены значения диагональных элементов в эВ, т.е. энергии E_s (верхнее число) и E_p (нижнее число), причем в матрицу эти значения энергии должны входить со знаком минус.

Таблица 28

II	III	IV	V	VI
—	—	C 17.52 8.97	—	—
—	Al 10.11 4.86	Si 13.55 6.52	P 17.10 8.33	S 20.80 10.27
Zn 8.40 3.38	Ga 11.37 4.90	Ge 14.38 6.36	As 17.33 7.91	Se 20.32 9.53
Cd 7.70 3.38	In 10.12 4.69	Sn 12.50 5.97	Sb 14.80 7.27	Te 17.11 8.59

Таким образом, Харрисон определил все матричные элементы ЛКАО-гамильтониана, представленного табл. 27. По энергиям E_s и E_p, приведенным в табл. 28, можно рассчитать закон дисперсии E(k) для 19 полупроводников IV, III и V, II и VI групп. Зонная структура этих полупроводников получается путем диагонализации матрицы (табл. 27), т.е. путем нахождения ее собственных значений для определенных точек k-пространства. С точки зрения теории энергетических зон, уровни E(k) ищутся по определенным направлениям k-пространства, о чем мы будем подробно рассказывать в следующих подразделах. На рис. 31а показаны зонные структуры Si и Ge, впервые полученные на основе матрицы гамильтониана Чади и Коэна (Харрисон, как было сказано, лишь упростил их расчет). К недостаткам метода ЛКАО нужно отнести неудовлетворительный вид ЗП. В частности, для зоны Si нарушено чередование основных состояний Г'₂ и Г₁₅; минимумы ЗП находятся не в тех местах k-пространства, где бы им нужно было находиться (в направлении Δ для Si и в точке Λ для Ge).

Рис. 31а

Левин [50] пошел по пути усложнения матричных элементов за счет учета влияния вторых и третьих соседей по решетке. Автор, видимо считал, что с увеличением числа варьируемых параметров матрица гамильтониана приобретет необходимую «гибкость», что позволит увеличить точность нахождения энергетических уровней. Однако вариационные возможности ЛКАО-гамильтониана весьма ограничены и определяются не столько конкретным видом матричных элементов, сколько небольшой размерностью самой матрицы. Дело в том, что для любой матрицы существует алгебраическое ограничение: сумма собственных значений диагонализированной матрицы равна сумме диагональных элементов исходной матрицы, поскольку обе матрицы, и исходная, и диагонализированная, связаны отношением подобия. Другими словами, на характер матрицы (или ее след) не влияет процедура диагонализации. В частности, для Ge выполняется безусловное равенство во всем k-пространстве (в соответствии с графиками E(Г'₂₅) = 0):

,

здесь имеется в виду 0,3 ридберга (напомним, единица энергии 1Ry = 13,63 эВ). Отсюда получается, что ЗП является зеркальным отображением ЗВ, поэтому, если подгоняется ЗВ, то ЗП оказывается предопределенной и, наоборот. Дж. Дрессельхауз и М. Дрессельхауз в 1966 г. опубликовали работу, где предлагали иную, чем у Чади и Коэна, матрицу гамильтониана размерностью 8 × 8 с 18 варьируемыми параметрами.

На рис. 31б приведены результаты нашего расчета по их данным. Из зонной структуры видно, что Дрессельхаузы добились нужного чередования состояний Г'₂ и Г₁₅ для Si и минимумы ЗП для обоих материалов у них находятся в нужных местах k-пространства. Однако им пришлось изменить кривизну самого важного уровня энергии Г₁, что противоречит квадратичной природе закона дисперсии E(k) для сферического s-состояния.

Рис. 31б

В заключение этого подраздела упомянем проблему неоднозначности. Харрисон привел числовую таблицу матричных элементов, составленную по результатам различных исследований, и написал: «Из сравнения различных значений из табл. 6.1 не всегда можно сделать однозначные выводы, так как в определенном смысле изменение матричного элемента B₁ может компенсировать изменение матричного элемента B₅. Поэтому матричные элементы определяются неоднозначно. Однако для понимания структуры энергетических зон не имеет значения, каким набором параметров из табл. 6.1 мы будем пользоваться» [49, т.1, с. 190 – 191].

С появлением неоднозначности матричных элементов теряется главное — физический смысл интегралов перекрывания атомных орбиталей. Что же касается «понимания структуры энергетических зон», то на основе метода ЛКАО оно нескоро дойдет до читателя, поскольку искажения зон слишком велики, чтобы по этим зонам можно было сделать какие-то физически осмысленные выводы. Модель ЛКАО слишком груба для столь сложного явления как дисперсия электронов и дырок на ядрах кристаллической решетки. Чтобы до конца понять механизмы рассеяния носителей зарядов, нам нужно изменить сам конструктивный подход к анализу распределения зарядов в обратном пространстве полупроводникового кристалла.