
Конструктивная математика
Акимов О.Е.
29. Закон дисперсии в рамках kp-модели
Закон дисперсии E(k), рассчитанный в приближении слабой связи, ведется через матричные элементы псевдопотенциала
< k + K' | V | k + K >,
входящие в матрицу гамильтониана, обычная размерность которой равна 100 × 100 плоским волнам. ЛКАО гамильтониан, составленный по модели сильной связи, имел у нас матрицу размерности 8 × 8. Сейчас мы познакомимся с моделью, которая дает матрицы гамильтонианов средней размерности 15 × 15 или 27 × 27, хотя потенциально они могут составляться очень небольшими, порядка 3 × 3, или, наоборот, большими, порядка 50 × 50; ограничений здесь никаких нет. Этот так называемый kp-метод лежит посередине между методами сильной и слабой связи. Его вычислительный потенциал огромен, но с точки зрения физики, он представляется достаточно искусственной конструкцией. По причине его простоты и эффективности им удобно пользоваться при анализе закона дисперсии. Впрочем, существует еще около десятка методов расчета с большим и средним числом матричных элементов, о которых мы умолчали.
Надо сказать, что положительной стороной теории конденсированного вещества является то, что она терпимо относится к самым различным конструктивным подходам. В ее арсенале мирно сосуществует множество модельных конструкций, которые не претендуют на истину в последней инстанции. Однако в теоретической физике есть области, где господствует консервативный формализм, когда ни одна буква в формулах не может быть изменена или иначе проинтерпретирована. Конструктивно настроенным исследователям там делать нечего, они должны всячески избегать подобных «заболоченных» мест науки. Но обратимся к нашему модельному kp-гамильтониану.
Свое название kp-метод получил от матричных элементов, которые представляют собой произведение волнового вектора k на величину импульса p. В этом методе, как и в предыдущих двух, действует так называемое адиабатическое приближение, которое позволяет пренебречь влиянием ядер на движение рассматриваемого электрона и, таким образом, позволяет отделить электронную систему кристалла от фононной. Здесь, как и в двух предыдущих случаях, так называемое зонное приближение предполагает, что кристаллический потенциал создан всей совокупностью атомных потенциалов, когда небольшие температурные отклонения отдельного атома или его дефектное расположение не может повлиять на строгую периодичность волновой функции. За счет взаимной компенсации случайных явлений, происходящих в кристаллической решетке, решение уравнения Шредингера ищется как для идеального монокристалла.
Если в исходное уравнение Шредингера подставить волновую функцию ψ(r + R), то для собственных значений энергии En(k) получим уравнение:
Hkunk = [p2/2m + ћkp/m + V(r)]unk = En(k)unk.
Слагаемое ћkp/m в гамильтониане Hk рассматривается как потенциал возмущения к основному потенциалу V(r). Решение последнего уравнения ищется в виде разложения unk по некоторой полной системе функций:
unk = Σm anm(k – k0)umk0,
в которой точка k достаточно близко отстоит от точки k0, так что разложение в ряд возможно.
Выделим в гамильтониане Hk невозмущенную часть Hk0, получим
[Hk0 + ћ(k – k0)p/m + ћ2(k2 – k02 )p/2m]unk = En(k)unk.
где Hk0 = p2/2m + ћk0p/m + ћ2k02 /2m + V(r). Подстановка разложенной функции unk в последнее выражение, умножение обеих частей уравнения на сопряженную функцию unk и интегрирование по элементарной кристаллической ячейке дает систему уравнений в виде следующей суммы
Σm {[En(k0) + ћ2(k2 – k02 )p/2m]δnm + ћ(k – k0)Pnm(k0)/m}anm = En(k)anm,
здесь Pnm(k0) = < unk0 | p | umk0 > — матричный элемент оператора импульса, δnm — символ Кронекера. Данная система уравнений разрешима, если ее определитель равен нулю, т.е.
det{[En(k0) – En(k) + ћ2 (k2 – k02 )p/2m]δnm + ћ(k – k0)Pnm(k0)/m} = 0.
Чтобы найти закон дисперсии En(k) по всему k-пространству в пределах первой ЗБ, нужно знать энергии En(k0) и матричные элементы импульса Pnm(k0). Энергии En(k0) берутся из эксперимента, а под них затем подгоняют матричные элементы Pnm(k0). Для составления матрицы гамильтониана Hk, в соответствии с последним уравнением необходимо знать еще структуру кристаллического материала, в качестве которого мы рассматриваем полупроводники Ge, Si, GaAs и т.д.
Симметричная матрица kp-гамильтониана (приводится ее верхняя треугольная часть) размерностью 15 × 15 с подогнанными матричными элементами оператора импульса pi = < un | p | um > для трех первых векторов обратной решетки: {000}, {111} и {200} представлены табл. 31. Ниже диагонали матрицы приведены значения энергии в симметричных точках ЗБ. Экспериментальные точки, по которым велась подгонка параметров импульса, выделены жирным шрифтом.
Таблица 31
| H1 | 0 | p4kz | 0 | 0 | 0 | 0 | 0 | 0 | p4ky | 0 | 0 | 0 | p4kx | 0 |
| H2 | p3kz | 0 | 0 | 0 | 0 | 0 | 0 | p3ky | 0 | 0 | 0 | p3kx | 0 | |
| H3 | p1ky | 0 | 0 | 0 | 0 | 0 | 0 | p2ky | 0 | p1kx | 0 | p2kx | ||
| H4 | 0 | p9kx | p10kx | 0 | bp5kx | p1kz | 0 | ap5kx | 0 | 0 | 0 | |||
| H5 | p7kz | p8kz | 0 | cp6kz | p2kx | 0 | 0 | 0 | p2ky | 0 | ||||
| i | Xi | Li | Гi | H6 | 0 | p9kz | 0 | 0 | p7kx | 0 | p9ky | 0 | p7ky | |
| 1 | 0.654 | 0.779 | 0.926 | H7 | p10kz | 0 | 0 | p8kx | 0 | p10ky | 0 | p8ky | ||
| 2 | 1.365 | 0.933 | 0.459 | H8 | cp5kz | p1kx | 0 | 0 | 0 | p1ky | 0 | |||
| 3 | 0.096 | 0.062 | 0.239 | i | Xi | Li | Гi | H9 | 0 | bp6kx | 0 | bp5ky | 0 | bp6ky |
| 4 | 0.272 | 0.566 | 0.000 | 10 | 0.829 | 0.309 | 0.239 | H10 | p2kz | 0 | 0 | 0 | 0 | |
| 5 | 1.455 | 1.040 | 0.909 | 11 | 1.626 | 1.720 | 0.909 | H11 | ap6kx | 0 | 0 | 0 | ||
| 6 | 0.096 | 0.573 | 0.073 | 12 | 1.014 | 0.933 | 0.669 | H12 | ap5ky | 0 | ap6ky | |||
| 7 | 2.642 | 2.295 | 0.992 | 13 | 0.272 | 0.110 | 0,000 | H13 | p1kz | 0 | ||||
| 8 | 0.654 | 0.110 | 0.000 | 14 | 0.829 | 0.309 | 0.239 | H14 | p2kz | |||||
| 9 | 0.829 | 0.933 | 0.669 | 15 | 1.626 | 1.720 | 0.909 | H15 |
В табл. 32 приведены матричные элементы импульса для Ge, Si и α-Sn по исследованиям других авторов, в частности, [53, с. 59]. Симплекс-методом подгонки параметров, который использовался нами во всех предыдущих случаях, можно добиться аналогичного результата меньшим числом параметров. В четвертой строке табл. 32 приведены параметры, найденные по симметричному направлению Δ, где известно максимальное число экспериментальных точек. Квадратичная ошибка для этого направления принимается за ноль (δ = 0). В пятой строке приведены десять оптимально найденных параметров, дающих минимальную ошибку (δ = 0,000721), вычисленную по всем известным экспериментальным точкам по Δ и L направлениям. Во всех последующих строках табл. 32 число параметров уменьшается. Например, в строке Ge(9) приведены девять параметров для германия. Два наиболее близких параметра, а именно: p6 и p9, принимались за один, и далее варьирование производилось уже по девяти параметрам.
Таблица 32
| δ·10–5 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 | |
| α-Sn | — | 1.002 | 0.389 | 0.952 | 0.356 | 0.641 | 1.272 | 0.557 | 1.079 | 1.120 | 0.038 |
| Si | — | 1.050 | 0.807 | 1.080 | 0.206 | 0.830 | 1.210 | 0.090 | 1.320 | 1.200 | 0.100 |
| Ge | — | 1.070 | 0.752 | 1.200 | 0.532 | 0.805 | 1.436 | 0.171 | 1.623 | 1.360 | 0.100 |
| Ge(Δ) | 0 | 1.1040 | 0.8780 | 1.1010 | 0.4486 | 0.8470 | 1.1290 | 0.1818 | 1.5800 | 1.1900 | 0.1000 |
| Ge(10) | 72 | 1.1319 | 0.7566 | 1.0765 | 0.4050 | 0.8430 | 1.1997 | 0.2658 | 1.2891 | 1.2176 | 0.4417 |
| Ge(9) | 73 | 1.1336 | 0.7533 | 1.0770 | 0.4045 | 0.8440 | 1.2068 | 0.2742 | 1.2857 | 1.2068 | 0.4509 |
| Ge(8) | 126 | 1.1110 | 0.7769 | 1.1110 | 0.4182 | 0.8600 | 1.1992 | 0.2407 | 1.2770 | 1.1992 | 0.4691 |
| Ge(7) | 272 | 1.1171 | 0.7578 | 1.1171 | 0.4199 | 0.8514 | 1.2179 | 0.2269 | 1.2179 | 1.2179 | 0.4659 |
| Ge(6) | 715 | 1.1634 | 0.7056 | 1.1634 | 0.4254 | 0.8560 | 1.1634 | 0.2056 | 1.1634 | 1.1634 | 0.6236 |
| Ge(6) | 295 | 1.1073 | 0.8286 | 1.1073 | 0.4203 | 0.8286 | 1.1073 | 0.1411 | 1.3084 | 1.3084 | 0.3592 |
| Ge(5) | 1430 | 1.1452 | 0.8104 | 1.1452 | 0.4206 | 0.8104 | 1.1452 | 0.1707 | 1.1452 | 1.1452 | 0.6968 |
| Ge(5) | 1156 | 1.1829 | 0.6792 | 1.1829 | 0.3666 | 0.8082 | 1.1829 | 0.3666 | 1.1829 | 1.1829 | 0.5321 |
| Ge(5) | 751 | 1.1536 | 0.7258 | 1.1536 | 0.4206 | 0.8657 | 1.1536 | 0.1805 | 1.1536 | 1.1536 | 0.7258 |
Таким образом, число параметров уменьшилось в два раза при ошибке δ ≈ 0,01. Тем самым была продемонстрирована неоднозначность параметров, поскольку вполне точную зонную структуру можно получить при совершенно различных значениях импульса. На рис. 47 энергетические зоны германия Ge(10) изображены сплошными линиями, Ge(5) (с ошибкой δ = 0,0075) — точечными линиями. Белыми кружками на этом рисунке обозначены экспериментальные точки.

Рис. 47
Число параметров для полупроводников, лишенных центра симметрии, увеличивается еще на шесть дополнительных. Приведем численные значения матричных элементов для GaAs с указанием их места расположения в гамильтониане:
< Г15 | p11 | Г '25 > = 0.121, < Г '2 | p12 | Г1u > = – 0.224,
< Г '2 | p13 | Г1 > = 0.324, < Г15 | p14 | Г '25u > = 0.156,
< Г '2u | p15 | Г1 > = 0.001, < Г '2u | p16 | Г1u > = – 0.209,Симметрия в центре ЗБ в точке Г в принятой системе обозначений будет следующая: Г '25 для уровней Г4, Г8, Г13; Г '25u для Г5, Г11, Г15; Г15 для Г3, Г10, Г14; Г '12 для Г9, Г12; Г1 для Г1; Г1u для Г2; Г '2 для Г6; Г '2u для Г7 (u – верхний). На диагонали матрицы стоят значения энергии Hi = Гi + kx2 + ky2 + kz2, где kx, ky, kz — координаты волнового вектора k = 2π/r0 (r0 = 5,292·10–9 — боровский радиус). В матрице фигурируют коэффициенты:
,
,
,
. Энергия E(k) измеряется в ридбергах (напомним, 1 Ry = 13,6 eV).
На матрице kp-гамильтониана разберем более детально, какие матричные элементы должны быть в принципе отличными от нуля, а какие равны нулю. Данный анализ распространяется на матрицы двух предыдущих приближений. Используя свойства линейного преобразования базиса можно факторизовать матрицу гамильтониана Г(15 × 15) по симметричным направлениям. Для направлений Λ и Σ будем иметь следующее разложение исходной матрицы на прямую сумму матриц меньшей размерности:
TΛГ(15 × 15)TΛ–1 = Λ1(7 × 7) + 2Λ3(4 × 4),
TΣГ(15 × 15)TΣ– 1 = Σ1(5 × 5) + Σ2(3 × 3) + Σ3(6 × 6) + Σ4(1 × 1).
Матрица гамильтониана Г(15 × 15) за счет добавления вектора {220}, которое дает 12 новых энергетических уровней, может быть расширена до размерности Г(27 × 27). Найдем совокупность неприводимых представлений, на которые распадается уровень с вектором {220} в кристаллическом пространстве кубической симметрии Oh, которую имеет алмаз. Задачу разложения приводимого представления на сумму неприводимых удобно начать с примера 6-лучевой звезды {100} ПК решетки (рис. 43а).
Под действием преобразований группы симметрии Oh вектора {100} переходят друг в друга. Например, поворот на угол p вокруг оси kx (C42) приводит к тому, что вектор (001), обозначенный через 1, переходит в вектор 4 (001), а этот, в свою очередь, займет положение 1. Векторы, обозначенные как 5 и 2, также меняются местами, а векторы 6 и 3 остаются на месте. Таким образом, это преобразование может быть записано матрицей, которая переставляет строки в векторе-столбце, а ее удобно представить подстановкой:
(14)(25) =
=
.
Характер этой матрицы равен h(C42) = 2. Характеры всех матриц-представителей 10 классов группы Oh для вектора {100} выписаны ниже:
h(E) = h[(1)] = 6, h(I) = h[(14)(25)(36)] = 0, h(C4) = h[(2653)] = 2, h(IC4) = h[(1245)(36)] = 0, h(C2) = h[(12)(36)(45)] = 0, h(IC2) = h[(26)(35)] = 2, h(C3) = h[(132)(456)] = 0, h(IC3) = h[(123456)] = 0, h(C42) = h[(14)(25)] = 2, h(IC42) = h[(36)] = 4. Аналогичным образом находим характеры для векторов {220}. Все результаты этих подсчетов занесены в последние строки таблицы характеров группы Oh (табл. 33)
Таблица 33
| Oh | E | 8C3 | 3C42 | 6C4 | 6C2 | I | 8IC3 | 3IC42 | 6IC4 | 6IC2 |
| Г1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Г2 | 1 | 1 | 1 | –1 | –1 | 1 | 1 | 1 | –1 | –1 |
| Г12 | 2 | –1 | 2 | 0 | 0 | 2 | –1 | 2 | 0 | 0 |
| Г '15 | 3 | 0 | –1 | 1 | –1 | 3 | 0 | –1 | 1 | –1 |
| Г '25 | 3 | 0 | –1 | –1 | 1 | 3 | 0 | –1 | –1 | 1 |
| Г '1 | 1 | 1 | 1 | 1 | 1 | –1 | –1 | –1 | –1 | –1 |
| Г '2 | 1 | 1 | 1 | –1 | –1 | –1 | –1 | –1 | 1 | 1 |
| Г '12 | 2 | –1 | 2 | 0 | 0 | –2 | 1 | –2 | 0 | 0 |
| Г15 | 3 | 0 | –1 | 1 | –1 | –3 | 0 | 1 | –1 | 1 |
| Г25 | 3 | 0 | –1 | –1 | 1 | –3 | 0 | 1 | 1 | –1 |
| Г{100} | 6 | 0 | 2 | 2 | 0 | 0 | 0 | 4 | 0 | 2 |
| Г{220} | 12 | 0 | 0 | 0 | 2 | 0 | 0 | 4 | 0 | 2 |
Для определения числа неприводимых представлений, содержащихся в приводимом представлении, необходимо воспользоваться соотношением:
где
.
Здесь Eα — неприводимые представления группы Oh; Eβ — приводимое представление группы векторов либо Г{100}, либо Г{220}; mα — число, указывающее сколько раз представление Eα содержится в Eβ; n = 48 — порядок группы Oh; hβ — характер приводимого представления (в нашем случае hβ равно либо h{100}, либо h{220}); hα — характеры неприводимых представлений группы Oh. Характеры этой группы, группы октаэдра, в которой существует центр инверсии, приведены в табл. 33.
Найдем, сколько раз неприводимое представление Г1 содержится в Г{100}:
 (6·1 + 8·0 + 3·2 + 6·2 + 6·0 + 1·0 + 8·0 + 3·4 + 6·0 + 6·2) = 1.
(6·1 + 8·0 + 3·2 + 6·2 + 6·0 + 1·0 + 8·0 + 3·4 + 6·0 + 6·2) = 1.
В приводимое представление Г{220} неприводимое представление Г1 тоже входит 1 раз. Но, например, представление Г '15 уже не входит в Г{220}:
 [12·1·3 + 0·8·0 + 0·3·(–1) + 0·6·1 + 2·6·(–1) + 0·1·3 + 0·8·0 + 4·3·(–1) + 0·6·1 + 2·6·(–1)] = 0.
[12·1·3 + 0·8·0 + 0·3·(–1) + 0·6·1 + 2·6·(–1) + 0·1·3 + 0·8·0 + 4·3·(–1) + 0·6·1 + 2·6·(–1)] = 0.
Окончательные результаты расчета дают следующие разложения:
Г{100} = Г1 + Г12 + Г15, Г{220} = Г1 + Г12 + Г15 + Г25 + Г '25.
В табл. 34 приведены разложения и для других звезд обратной решетки.
Таблица 34
Г1 Г2 Г12 Г '15 Г '25 Г '1 Г '2 Г '12 Г15 Г25 {000} 1 0 0 0 0 0 0 0 0 0 {100} 1 0 1 0 0 0 0 0 1 0 {111} 1 0 0 0 1 0 1 0 1 0 {200} 1 0 0 0 1 0 1 1 0 0 {220} 1 0 1 0 1 0 0 0 1 1 {311} 1 0 1 1 2 0 1 1 2 1 {222} 1 0 0 0 1 0 1 0 1 0 {400} 1 0 1 0 0 0 0 0 1 0 Пусть {φi} есть некоторое пространство функций, преобразующихся по приводимому представлению Гβ. Можно выбрать из {φi} такие линейные комбинации, которые бы преобразовывались только по соответствующим неприводимым представлениям Гα. С этой целью из неприводимых представлений Гα строим проекционный оператор, по стандартной методике [54], [55]:
,
где n — порядок группы Oh, nα — размерность матриц неприводимого представления Гα, P(R) — конкретный матричный оператор группы Oh, R — пробегает все элементы группы Oh, которой описывается алмазная решетка полупроводников Ge и Si.
Итак, нам нужен набор функций и набор матриц группы Oh. Можно было бы воспользоваться ортогональными матрицами группы октаэдра O [4, c. 234] однако, во-первых, группа Oh не совсем одно и то же, что группа O; во-вторых, в формуле для проекционного оператора ничего не говорится об ортогональности, т.е. матрицы могут быть общего вида, не обязательно ортонормированными на единицу; в-третьих, нам не мешало бы лучше усвоить на практике процедуру составления матриц представления по заданным базисным функциям. Набор симметризованных функций приведен в табл. 35.
Таблица 35
Гα Состояния Симметризованные базисные функции Г1 s 1 Г15 px, py, pz x, y, z Г '25 d1, d2, d3, xy, yz, zx Г12 d3, d4 3z2 – r2, x2 – y2 Г25 f1, f2, f3, z(x2 – y2), x(y2 – z2), y(z2 – x2) Г '2 f4 xyz Г '15 g1, g2, g3, xy(x2 – y2), yz(y2 – z2), zx(z2 – x2) Г '12 h1, h2 xyz(3z2 – r2), xyz(x2 – y2) Г2 i z4(x2 – y2) + x4(y2 – z2) + y4(z2 – x2) Г '1 j xyz[z4(x2 – y2) + x4(y2 – z2) + y4(z2 – x2)] Теперь начинаем конструировать матрицы неприводимых представлений группы Oh. Матрицами всех одномерных представлений являются сами характеры этих представлений. В отношении трехмерных представлений Г15 и Г '25, отвечающие p- и d-орбиталям свободных атомов, т.е. не находящихся в кристаллической решетке (рис. 42), также никаких проблем не возникает. В частности, для преобразования, входящего в класс С3, двумя конкретными матрицами представления являются
Г15 (С3) =
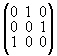
, Г '25 (С3) =

.
Несколько сложнее отыскать матрицы двумерного представления Г12. Базисными функциями этого неприводимого представления являются {2z2 – x2 – y2, x2 – y2}. Преобразование С3, по сути, производит циклическую перестановку координат x → y → z → x. Значит, нужно найти такие числа a, b, c и d, чтобы выполнялось условие:
.
Выписав из таблицы характеров (табл. 33) характер (–1), соответствующий представлению Г12, для восьми (четыре прямых и четыре инверсных — 8C3) поворотов куба вокруг его пространственных диагоналей, присваиваем a = d = –½ (хотя кому-то могут больше понравиться другие значения, например: a = –¾, d = –¼). Далее ищем по двум уравнениям два оставшихся неизвестных b и c. В итоге получим
Г12 (С3) =
.
Так или примерно так поступаем во всех случаях, когда нужно по таблице характеров и набору базисных функций восстановить неизвестные матрицы представлений по известной группе преобразования декартовых координат. Все матрицы группы Oh искать, конечно, не нужно; достаточно построить матрицы образующих группы, чтобы по ним, путем перемножения, получить все недостающие матрицы.
Итак, все матрицы неприводимых представлений Г1, Г12 и Г15, на которые распадается приводимое представление Г{100}, найдены. Тогда, используя проекционный оператор и 6-лучевой базис {1, 2, 3, 4, 5, 6} состояния Г{100}, найдем новый, штрихованный базис {1', 2', 3', 4', 5', 6'} для прямой суммы неприводимых представлений:
Г1 : 1' = 1 + 2 + 3 + 4 + 5 + 6,
Г12 : {2' = – 1 – 2 + 2·3 – 4 – 5 + 2·6, 3' = 1 – 2 + 4 – 5},
Г15 : {4' = 1 – 4, 5' = 2 – 5, 6' = 3 – 6}.С помощью трансформационной матрицы Т, а лучше — построчного преобразования векторов, произведем разложение матрицы приводимого представления Г{100} на прямую сумму матриц неприводимых представлений Г1, Г12 и Г15. В качестве примера возьмем конкретную матрицу, записанную в базисе {1, 2, 3, 4, 5, 6}, и преобразуем ее в квазидиагональный вид посредством базиса {1', 2', 3', 4', 5', 6'}:
→
=
.
Проверяем:
1' = 1 + 6 + 2 + 4 + 3 + 5 = (1) · 1',
2' = – 1 – 6 – 4 – 3 + 2 · 2 + 2 · 5 = (–½) · 2' + (–3/2) · 3',
3' = 1 – 6 + 4 – 3 = (–½) · 2' + (½) · 3',
4' = 1 – 4 = (1) · 4',
5' = 3 + 6 = (–1) · 6',
6' = 2 – 5 = (1) · 5'.Поиск 12 базисных функций для неприводимых представлений Г1, Г12, Г15, Г25 и Г '25 для интересующего нас состояния Г{220} ничем не отличается, разве что своей громоздкостью. После того, как найдены неприводимые представления и базисные функции, можно приступать к составлению матрицы гамильтониана Г(27 × 27). Сейчас нам понадобятся правила отбора матричных элементов.
Матричные элементы только тогда отличны от нуля, когда прямое произведение представлений, стоящих в матричном элементе, содержит единичное представление. Для любого матричного элемента центральным множителем является импульс, преобразующийся по представлению радиус-вектора (x, y, z), т.е. по представлению Г15. Кроме того, можно показать [55], что достаточно выполнить условие
Гα × Г15 = Гβ + Σδ Гδ,
для матричного элемента импульса < Гα | p | Гβ >, чтобы выполнялось и условие
Гα × Г15 × Гβ = Г1 + Σδ Гδ.
Раскладывать произведение представлений на прямую сумму мы уже умеем, поэтому сразу приведем результат:
Г '25 × Г15 = Г15 + Г25 + Г '12 + Г '2.
Отсюда автоматически следует, что
< Г '25 | p(Г15) | Г '12 > ≠ 0; но < Г '25 | p(Г15) | Г12 > = 0.
Проведенные вычисления показали, что общее число матричных элементов, отличных от нуля, в гамильтониане Г(27 × 27) равно 27 (числа совпали случайно). Для поиска числовых значений матричных элементов импульса матрицу Г(27 × 27) необходимо факторизовать по симметричным направлениям, поскольку одновременное варьирование по 27 свободным параметрам даст слишком большую неоднозначность. Под словом «факторизация» в данном случае понимается разложение одной большой матрицы на прямую сумму нескольких матриц меньшей размерности, т.е. сведение исходной матрицы к квазидиагональному виду. Однако технически эта операция выполняется намного проще, чем вышеописанная процедура перехода от нештрихованного базиса для Г{100} и Г{200} к штрихованному, где они тоже принимают квазидиагональный вид. Так, чтобы матрица Г(27 × 27) распалась на совокупность Δ-матриц, принимают kx = ky = 0, kz — переменная; тогда получают
2·Δ1(6 × 6), Δ2(2 × 2), 2·Δ5(6 × 6), Δ'1(1 × 1).
Но и эта простая процедура попадает под операцию подобия; для двух других симметричных направлений будем иметь следующие прямые суммы:
TΛГ(27 × 27)TΛ–1 = Λ1(10 × 10) + Λ2(1 × 1) + 2·Λ3(8 × 8),
TΣГ(27 × 27)TΣ–1 = Σ1(10 × 10) + Σ2(5 × 5) + Σ3(8 × 8) + Σ4(4 × 4).
В табл. 36 верхняя часть является симметричной матрицей Λ1(10 × 10), нижняя часть — матрица Λ3(8 × 8), матрица Λ2(1 × 1) = H9; в табл. 37 верхняя часть — матрица Σ1(10 × 10), нижняя — матрица Σ3(8 × 8); в табл. 38 верхняя часть — матрица Σ2(5 × 5), нижняя — матрица Σ4(4 × 4); коэффициенты во всех таблицах равны: с1 = 1.1547, с2 = –0.5774, с3 = 0.7071, с4 = 0.5, с5 = 0.866. Далее методом варьирования находят значения всех 27 параметров, опираясь на известные 10. В табл. 39 приведена совместимость центральной точки Г ЗБ с ее направлениями Δ, Λ и Σ.
Таблица 36
| H1 | 0 | 0 | p1k | 0 | 0 | 0 | p2k | 0 | 0 |
| H2 | p9k | c1p7k | 0 | 0 | p10k | c1p8k | 0 | 0 | |
| H2 | H3 | 0 | 0 | p15k | 0 | 0 | p21k | 0 | |
| c2p7k | H4 | H4 | p3k | c1p13k | 0 | 0 | c1p19k | p5k | |
| c3p12k | 0 | H6 | H5 | 0 | 0 | p4k | 0 | 0 | |
| 0 | c2p13k | c3p18k | H7 | H7 | p16k | c1p14k | 0 | 0 | |
| c2p11k | 0 | 0 | c2p17k | H9 | H8 | 0 | p22k | 0 | |
| 0 | c3p25k | 0 | 0 | c3p27k | H10 | H11 | c1p20k | p6k | |
| c2p8k | 0 | 0 | c2p14k | 0 | c3p26k | H11 | H12 | 0 | |
| 0 | c2p19k | 0 | 0 | 0 | 0 | c2p20k | H12 | H13 |
Таблица 37
| H1 | 0 | p1k | 0 | 0 | 0 | 0 | p2k | 0 | 0 |
| H2 | p7k | 0 | 0 | p11k | 0 | p8k | 0 | 0 | |
| H2 | H4 | p3k | p13k | 0 | p25k | 0 | p19k | p5k | |
| p9k | H3 | H5 | 0 | 0 | 0 | p4k | 0 | 0 | |
| p7k | 0 | H4 | H7 | p17k | 0 | p14k | 0 | 0 | |
| c4p12k | 0 | 0 | H6 | H9 | p27k | 0 | p23k | 0 | |
| 0 | p15k | p13k | c4p18k | H7 | H10 | p26k | 0 | 0 | |
| p10k | 0 | 0 | 0 | p16k | H8 | H11 | p20k | p6k | |
| p8k | 0 | 0 | 0 | p14k | 0 | H11 | H12 | 0 | |
| 0 | p21k | p19k | c4p24k | 0 | p22k | p20k | H12 | H13 |
Таблица 38
| H2 | c5p12k | 0 | p11k | 0 |
| H6 | c5p18k | 0 | c5p24k | |
| H11 | H7 | p17k | 0 | |
| p26k | H10 | H9 | p23k | |
| 0 | p27k | H9 | H12 | |
| 0 | p25k | 0 | H4 |
Таблица 39
| Г1 | Г2 | Г12 | Г '15 | Г '25 | Г '1 | Г '2 | Г '12 | Г15 | Г25 |
| Δ1 | Δ2 | Δ1Δ2 | Δ'1Δ5 | Δ'2Δ5 | Δ '1 | Δ '2 | Δ '1Δ '2 | Δ1Δ5 | Δ2Δ5 |
| Λ1 | Λ2 | Λ3 | Λ2Λ3 | Λ1Λ3 | Λ2 | Λ1 | Λ3 | Λ1Λ3 | Λ2Λ5 |
| Σ1 | Σ4 | Σ1Σ4 | Σ2Σ3Σ4 | Σ1Σ2Σ3 | Σ2 | Σ3 | Σ2Σ3 | Σ1Σ3 Σ4 | Σ1Σ2Σ4 |