Конструктивная математика

Акимов О.Е.

9. Математика древних

Важную роль в распространении математических знаний сыграли греческие первоисточники, в частности, «Начала» Евклида, которые переводилась на языки европейских народов, почти вслед за Библией. Именно благодаря этой книге через посредничество арабов возникла современная наука. Правда, существует мнение, что главный центр математических исследований после увядания эллинской культуры переместился не к арабам, а к индийцам, которые имели свою систему счисления, ввели отрицательное число и ноль, внедрили некоторые методические новшества. И только после брожения в течение двух-трех веков математикой заинтересовались арабы.

Естественно, возникает вопрос: могла бы та же рациональная наука возникнуть в Европе без задела греческих математиков? Сейчас, по-видимому, сложно ответить однозначно, распространялись ли знания по типу цепной реакции или же они возникали в основных центрах цивилизации — Китае, Индии, Египте, Вавилоне и Греции. До каких-то истин люди доходили, безусловно, самостоятельно (по аналогии с религией: идеями Бога, рая, ада, нечистой силы и т.д.), а какие-то знания заимствовали у своих соседей (если опять же говорить о религии, это в первую очередь специфические обряды и культы, такие, например, как крестное знамение). То, что первобытные народы способны без посторонней помощи, практически из ничего создать сложные вычислительные алгоритмы, демонстрируют различия в процедурах умножения и деления больших чисел.

Наиболее употребительной операцией было умножение или деление на 2. Именно поэтому, видимо, в Египте установилась бинарная форма арифметического счета, которая сегодня у нас используется в компьютерах. Например, необходимо было умножить 37 на 46. Древнеегипетский математик поступал следующим образом: он составлял ряд степеней двойки и против каждого элемента этого ряда записывал второй сомножитель, предварительно перемножив его на элемент первого ряда. Затем он из первого ряда выбирал те степени числа 2, которые в сумме давали 37, а из второго ряда соответствующие числа давали в сумме искомое произведение (табл. 2)

Таблица 2

1	2	4	8	16	32
46	92	184	368	736	1472

37 · 46 = 1702, 1 + 4 + 32 = 37, 46 + 184 + 1472 = 1702.

Процедура деления чисел осуществлялась аналогично. Покажем на числах, что нужно было сделать, чтобы разделить 153 на 17 (табл. 3).

Таблица 3

1	2	4	8
17	34	68	136

153 : 17 = 9, 17 + 136 = 153, 1 + 8 = 9.

Задача 32 папируса Ринда демонстрирует алгоритм возведения в квадрат числа 12. Алгоритм оформлен в виде табл. 4, в левой части которой он представлен на языке древнеегипетских иероглифов, в правой записан современными цифрами. Древнеегипетские иероглифы читаются справа налево, причем символ I означает единицу, ∩ — 10, ς — 100; результат изображался в виде свернутого папируса с печатью наверху. Правая часть таблицы является зеркальным отображением левой с той только разницей, что все числа записаны в современном виде. Первый множитель составлялся из определенного набора степеней 2; в данном случае 12 = 4 + 8 = 2² + 2³ (цифры 4 и 8 писец отмечал штрихом). Второй столбец чисел начинался со значения второго множителя, который у нас равен тоже 12. Последующие числа получаются путем удвоения предыдущих. Результат находится как сумма чисел второго столбца, взятых из отмеченных штрихом строк: 144 = 48 + 96.

Таблица 4

2000 лет до Р.Х.		2000 лет после Р.Х.
I I ∩	I	1	12
I I I I ∩ ∩	I I	2	24
I I I I ∩ ∩ I I I I ∩ ∩	I I I I '	4'	48
I I I ∩ ∩ ∩ ∩ ∩ I I I ∩ ∩ ∩ ∩	I I I I ' I I I I	8'	96
		Результат
I I I I ∩ ∩ ∩ ∩ ς		144

Теперь перенесемся в Китай и посмотрим, как там производилось умножение и деление, для чего ниже мы разберем два примера.

Пусть требуется перемножить число 275 на 34; составлялась табл. 5. Промежуточные и конечный результаты счета заносятся в среднюю строку, расположенную между строками двух сомножителей; умножение начинается с высших порядков: сотен — 2, затем десятков — 7 и, наконец, единиц — 5; использованные порядки отбрасываются; конечный результат (9350) получается на шаге VI; в последней графе приведены действия, которые необходимо было произвести в уме.

Таблица 5

I	II	III	IV	V	VI	Действия в уме
275	75	75	5	5		68 = 34 · 2, 89 = 68 + 3 · 7
68	68	89	918	933	9350	918 = 890 + 4 · 7, 933 = 918 + 3 · 5
34	34	34	34	34		9350 = 9330 + 4 · 5

Деление (8892 : 26 = 342) показано в табл. 6.

Таблица 6

I	II	III	IV	V	Действия в уме
3	3	34	342		2892 = 8892 – 2 · 3 · 1000,
8892	2892	1092	52	342	1092 = 2892 – 6 · 3 · 100,
26	26	26	26		52 = 1092 – 4 · 26 · 10

В других странах с доисторических времен существовали другие алгоритмы, по которым производились арифметические действия. В Индии, например, составлялись и заучивались наизусть специальные числовые таблицы умножения, возведения во вторую и третью степени (соответственно, извлечение квадратных и кубических корней), в которых порядок чисел измерялся сотнями тысяч. Все это говорит о том, что люди начинали конструктивно думать, не дожидаясь пока их кто-нибудь этому обучит. До нас дошли тысячи глиняных табличек с вавилонской клинописью, где приведены сложнейшие задачи практического содержания, причем с ними работали отнюдь не избранные ученые, а рядовые школьники в самом массовом порядке.

Общим местом стало утверждение, что Древняя Греция является родиной формально-логического подхода к геометрии. Однако бытует мнение, что во второй книге «Начал» Евклида приведен формализованный перечень математических (как арифметических, так и геометрических) правил, которыми «по умолчанию» с давних времен пользовались вавилоняне. Приведем и мы этот перечень из десяти предложений, которые записаны в стилизованном виде [11, с. 131 — 132]:

1) если a = a₁ + a₂ + ... + a_n, то ab = a₁b + a₂b + ... + a_nb;
2) если a = b + c, то a² = ab + ac;
3) если a = b + c, то ad = bd + cd;
4) (a + b)² = a² + b² + 2ab;
5) (a – b)b + (b – a/2)² = a²/4;
6) (a + b)² = a² + b² + (2a + b)b;
7) если c = a + b, то a² = b² + c² – 2bc;
8) (a + 2b)² = a² + 4(a + b)b;
9) [(a + b)²/2 + (a – b)²/2] = (a² + b²)/2;
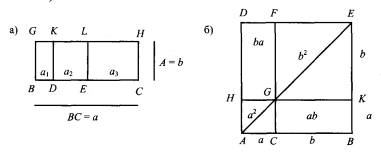
10) (a + b)² + b² = 2(a/2) 2 + 2(a/2 + b)².

Первое предложение Евклидом формулируется при помощи площадей прямоугольников: прямоугольник BH = ab равен сумме прямоугольников BK = a₁b, DL = a₂b, EH = a₃b (рис. 1 а). Всякий здравомыслящий человек, в том числе и древний вавилонянин, посчитает бессмысленным тратить время на вычерчивание рисунка и выписывание символов для предложения, которое и без того всем очевидно. Греки же страдали какой-то прямо-таки патологической формой графомании. Всякий, бросивший мельком взгляд на рис. 1б, поймет справедливость предложения 4 (на нашем рисунке малый и большой квадраты, а также прямоугольники мы еще обозначили величинами a², b², ab и ba, из которых моментально вытекает формула разложения квадрата суммы двух величин).

Но как поступает Евклид? Он пускается в нудное пережевывание самых тривиальных предложений. Чтобы читатель почувствовал всю эту схоластику и скуку, которые потом захлестнули Европу и держали ее полторы тысячи лет в дремоте, мы приведем целиком евклидово доказательство предложения 4: «Если прямую AB в точке C разделить на какие-нибудь две части AC и CB, то квадрат, построенный на AB, равен сумме квадратов, построенных на отрезках AC и CB с удвоенным прямоугольником, заключенным между отрезками AC и CB [рис. 1б]. Так как CF параллельно BE, то угол AGC равен AEB (I.29). Но AB равно BE (I.5), следовательно, углы AEB, EAB и AGC равны между собой, откуда (I.6) AC равно CG. Кроме того, AC и CG равны противоположным сторонам GH и AH (I.34), следовательно, CH есть равносторонний четырехугольник. Так как CF параллельно HA, то (I.29) сумма углов HAC и GCA равна 2d. Но угол HAC — прямой, следовательно, и угол GCA тоже прямой, оба эти угла равны противоположным углам HGC и AHG (I.34). Из этого видно, что CH есть равносторонний прямоугольник, следовательно, он является квадратом. Точно так же легко показать, что FK есть квадрат, сторона которого KG равна BC. Прямоугольник BG равен произведению сторон BC на CG или AC на BC, точно так же прямоугольник GD равен произведению AC на BC, но прямоугольник BG равен прямоугольнику GD (I.43), следовательно, сумма прямоугольника BG и прямоугольника GD равна удвоенному произведению AC на BC. Откуда прямоугольник ABED равен квадрату AB, а он равен сумме квадрата AC, квадрата BC и удвоенного квадрата AC на BC» [11, c. 128].

Рис. 1

Широко распространенное мнение о том, что аристотелевская (а до него элейская) логика способствовали возникновению и развитию естествознания, на наш взгляд, является глубоко ошибочным. Логика может только сдерживать математические и естественные науки, основывающиеся на представлениях. Она создает ложное впечатления строгой науки, в действительности же в ее многословии легко утонуть, что, собственно, и произошло спустя два-три столетий после Аристотеля. Взгляните на рис. 2а; древнеиндийский математик Бхаскара вычерчивал данный чертеж и говорил своим ученикам единственное слово: «Смотрите!» Кто не смог увидеть в нем формулы c² = a² + b², тот должен был заняться разведением кур или строительством домов, но только не математикой — туда для него путь был закрыт навсегда. Древнекитайский математик также рисовал рис. 2б (он есть в «Трактате о чжоу-би» Чжан Цзюнь-циня, II или III век) и, быть может, лишь из педагогических соображений, для нерадивых учеников выписывал формулу: c² = 4(ab/2) + (a – b)² = a² + b² (этой формуле удовлетворяет и рис. 2а). Вавилонские или египетские математики, возможно, держали перед глазами другой чертеж, например тот, что, состоял из двух квадратов, показанных на рис. 2в и рис. 2г. Квадраты прямо говорят о справедливости теоремы Пифагора, без всяких манипуляций символами.

А теперь полюбуйтесь, какой чертеж (рис. 2д) и какое доказательство сочинил Евклид. «Во всяком прямоугольном треугольнике, — пишет он в Предложение 47 своей первой книги «Начал», — квадрат, построенный на стороне, противолежащей прямому углу (на гипотенузе), равен сумме квадратов, построенных на сторонах, заключающих прямой угол (на катетах). В самом деле, угол A — прямой, прямыми являются углы BAC, BAG, HAC, следовательно, прямые AC и AG, BA и AH находятся: первые две — на одной прямой CG, а вторые две — на прямой BH. Проведем AL параллельно BD. Так как угол DBC равен углу FBC (аксиома 10), то, прибавляя к обеим частям по углу CBA, получим угол DBA, равный углу FBC (аксиома 2). Но AB равно BF, BC равно BD, следовательно, треугольник ABD равен треугольнику FBC (предложение 4). Заметив теперь, что BD параллельна AL и BF параллельна GC, имеем: четырехугольник BL равен двум треугольникам ABD и четырехугольник GB равен двум треугольникам FBC (предложение 41). Но треугольник ABD равен треугольнику FBC, следовательно, четырехугольник BL равен квадрату BG (аксиома 6). Точно так же можно показать, что четырехугольник LC равен квадрату CH. Откуда (аксиома 2): квадрат BC равен сумме квадратов AB и AC».

Рис. 2

Это доказательство, хотя и проведено логически верно, имеет, однако, низкую эвристическую ценность, так как при таком проведении вспомогательных линий (AD, AE, BK и CF) учащийся не мог представить себе, почему же сумма двух меньших квадратов должна быть равна третьему, большему квадрату. Нерациональное евклидово доказательство теоремы Пифагора комментаторы тут же исправляли: вслед за рис. 2д сразу же в примечании шел, к примеру, рис. 2е, сопровождающийся соответствующими выкладками, но и они были излишни. Никакой «математической культуры» (на это часто ссылаются) цепочка из символов не несет. С точки зрения педагогики, лучшей подсказкой для учащихся здесь будет рекомендация по вырезанию из бумаги соответствующих кусков и укладка их на плоскости чертежа. В общем, геометрия не нуждается в логике и, если она туда попала, то только для схоластических, а не эвристических целей, т.е. для целей школьного образования в самых его ретроградных формах. На примере этой теоремы отчетливо видно, как простота и рациональность могут быть принесены в жертву фальшивому мудрствованию. Сначала подобные доказательства были выдвинуты софистами нарочно, чтобы сбить спесь с «умников» и набить себе цену в глазах родителей. Но потом этот формализм лег в основу школьного и университетского образования, где во многом указанная мотивировка сохранилась. Раньше астрология, возникнув внутри астрономии, погубила точные науки вавилонян, теперь софистская логика, паразитирующая на геометрии и арифметике, погубила точные науки эллинов.

Когда произносят панегирики Евклиду, вспоминаются слова Артура Шопенгауэра из его известного сочинения, из первой книги «Мир как представление», где он говорит: «Часто, как это сделано в теореме Пифагора, проводятся линии, неизвестно для чего; впоследствии оказывается, что это были сети, которые неожиданно затягиваются и ловят согласие учащегося, вынужденного, к своему удивлению, признать то, что по своей внутренней связи остается ему совершенно непонятным — до такой степени, что он может проштудировать всего Евклида, не достигнув действительного понимания законов пространственных отношений и вместо этого заучивает наизусть лишь несколько выводов из них» [12, c. 204 —205]. Немецкий философ прекрасно понимал преимущества представления перед понятиями и, особенно преимущества зрительного образа перед схоластическими выкладками в духе Аристотеля. Шопенгауэр во многом ошибался, но отрицательную роль логики в деле познания он оценивал правильно. «... Логические методы Евклида в математике, — пишет он чуть ниже, — являются ненужной предосторожностью, костылем при здоровых ногах, кто следует этим методам, подобен путнику, который, приняв ночью светлый, твердый путь за воду, остерегается ступить на него и идет все время рядом по ухабам...» [12, c. 206]. Отчего не доверять своим глазам, почему нужно исписать страницы путаного и занудного текста, чтобы читающий не смотрел пристально на чертеж, а без конца прыгал глазами туда-сюда, от чертежа к тексту и, в конце концов, сдавшись на пытки автора, прекратил чтение.

Рис. 3

Взгляните на рис. 3а, он доказывает, что площадь треугольника равна площади прямоугольника, т.е. произведению основания a на половину высоты h (S = ah/2). Теперь взгляните на рис. 3б, он тоже самым непосредственным образом доказывает, что площадь круга равна половине прямоугольника, т.е. половине от произведения длины окружности l = 2πr на радиус r (S = lr/2 = πr²): чем больше число секторов, тем точнее формула — разве это интуитивно не ясно? К чему буквы и словеса — чтобы прикрыть слишком откровенную наготу истины или чтобы предать простым вещам наукообразный вид? Эти рисунки приводились в древнеиндийских учебниках по математике без всяких комментариев. Подсказки, наводящие вопросы иногда нужны, когда имеешь дело со сложными формами или объемными фигурами, но не в случае с теоремой Пифагора или, как в данном случае, с площадью плоских фигур. Здесь логика пусть отдыхает — не ее это дело, улавливать площади геометрических фигур, это дело только воображения, которое не нуждается в символах.

Считается, что «Начала» Евклида являются и началом греческой математики. Но сугубо формально-логический характер содержания этой книги говорит нам скорее о закате конструктивного знания. Эллины переняли у более древних народов уже готовые результаты и облекли их в схоластическую форму. В том виде, в котором геометрия представлена в учебнике Евклида, она никогда бы не возникла самостоятельно. Именно из-за своей крайней спекулятивности «Начала» были с готовностью приняты средневековыми университетами. Схоласты передавали из поколения в поколения мертвые знания, которые, как и библейские сказания, не имели отношения к рациональной науке, зато они выполняли важный социально-идеологический заказ по манипуляции сознанием наиболее интеллектуальной части общества.

Чтобы почувствовать разницу между формальным методом и конструктивным, давайте проанализируем еще один широко распространенный математический метод. Имеется в виду метод ложного положения, которым владели практически все древние народы — индийцы, арабы, вавилоняне и даже европейцы Средневековой эпохи. Не надо думать, что его передавали, как эстафету, из рук в руки одни древние народы другим. Доказательством тому служат некоторые задачи из египетских папирусов типа «аха», которые появились задолго до появления вавилонских табличек и вряд ли могли попасть в Месопотамию.

Слово «аха» можно перевести как «куча» или «множество», т.е. то неизвестное количество, которое необходимо найти и которое мы, люди начала третьего тысячелетия, обозначаем как x. Вот, например, как выглядят условие и решение задачи 26 ранее упомянутого древнеегипетского папируса Ринда: «Аха и ее четвертая часть вместе дают 15». Древнеегипетский писец предлагал алгоритм нахождения «аха»: «Считай с 4; от них ты должен взять четверть, а именно — 1; вместе — 5». Затем нужно было произвести еще два действие: деление — 15/5 = 3 и умножение — 3 · 4 = 12. Таким образом, находилась неизвестная «аха»: x = 12.

Сегодня бы эту задачу мы решали путем составления уравнения и решения его относительно неизвестного x:

x + (1/4) · x = (5/4) · x = 15,    x = (15/5) · 4 = 12.

Древний египтянин же использовал, как мы сказали, метод ложного положения. В нем положение x занимает некоторое число 4, от которого легко подсчитывается четвертая часть. Вместо 4, можно было бы взять, скажем, 8. Тогда четвертая часть равнялась бы 2, что в сумме с 8 давало бы 10. Но результат, предложенный данным алгоритмом, окажется тем же, т.е. x = (15/10) · 8 = 12.

Приведем задачу из Московского папируса, который так же, как и папирус Ринда, написан в эпоху Среднего царства, но в котором число задач в четыре раза меньше, чем в папирусе, хранящимся в Лондоне, т.е. свыше 20 штук. Кстати, размеры папирусов также отличаются примерно в 4 раза: папирус Ринда имеет площадь 525 · 33 см², а Московский — 544 · 8 см².

Итак, задача 19 из папируса, находящегося в Пушкинском музее в Москве, формулируется так: «1 плюс 1/2 аха вместе с 4 дают 10. Что есть аха? Подсчитай число, на которое 10 превышает 4. Получишь 6. Сколько раз надо взять 1 + 1/2, чтобы получить 1? Это число равно 2/3. Возьми 2/3 от 6. Получишь 4. Ответ найден верно». В данном случае древнеегипетский математик решал уравнение x + (1/2) · x + 4 = 10 примерно так же, как это сделали бы мы сегодня, т.е. без всякого «ложного положения»:

(3/2) · x = 10 – 4 = 6,     x = 6 · (2/3) = 4.

Наш соотечественник, видный историк науки С.Я. Лурье в комментариях к лекциям известного исследователя и историка науки Отто Нейгебауера о задаче рассматриваемого здесь типа писал следующее: «... Если решить эту задачу тем арифметическим способом, который широко применялся в индийской и арабской математике и который, скорее всего, восходит к Вавилону, именно методом ложного предположения, то каждое из действий, применяемых в тексте, получит свой смысл и не окажется никакой нужды в нынешней алгебре» [13, c. 205].

Действительно, метод ложного положения или, как сказал Лурье, метод ложного предположения — это мощный конструктивный прием. Однако сразу же отметим, что он не может служить альтернативой геометрическим методам и не в состоянии объяснить многие формулы, которыми пользовались древние математики. Что же касается передачи этого метода от вавилонян к индийским и арабским математикам, то в это верится с трудом. Клинопись вавилонян была забыта вместе с закатом их древней цивилизации. Археологические находки в виде глиняных табличек были обнаружены и расшифрованы сравнительно недавно. Нет никаких свидетельств тому, что арабы и индийцы могли читать вавилонскую клинопись. Арабская индийская и вавилонская культуры — это три абсолютно не пересекающихся сферы, разнесенные на многие века во времени. Между тем не такой уж это хитрый интеллектуальный ход, чтобы индийцы и арабы не могли догадаться до метода ложного положения самостоятельно.

В Древнем Египте средства письма и само письмо еще не были достаточно развитыми, поэтому условия задач и алгоритм их решение имели исключительно лаконичную форму. Многие знания передавались из «уст в уши» без какой-либо записи на материальных носителях. Если последние и использовались, то только для фиксации трудно запоминаемой информации, как в случае с каноническим разложением дробей вида 2/n. Это говорится к тому, что в папирусе Ринда есть иероглифические тексты, которые трудно назвать условием и алгоритмом решения какой-либо задачи. Непосвященному, действительно, сложно было догадаться, о чем, собственно, идет речь. Ниже приводится одна из таких задач. Непосредственная расшифровка ее нескольких иероглифов дала следующий набор слов и чисел: «Лестница, дом — 7, кошка — 49, мышь — 343, колос — 2401, зерно — 16807, один — 2801, два — 5602, четыре — 11204, вместе — 19607».

Исходя из чисел, сразу становится понятным, что данная задача касается суммы пяти членов геометрической прогрессии: 7 + 7² + 7³ + 7⁴ + 7⁵ = 19607. Египетский жрец геометрическую прогрессию обозначил иероглифом «лестница». Устный текст для этой задачи мог бы звучать приблизительно так: «Представьте себе улицу, где стоят семь домов. В каждом доме проживает по семь кошек. Каждая кошка съедает по семь мышей. Каждая мышь съедает по семь колосков. На каждом колоске находится по семь зерен. Требуется определить размер ахи». В папирусе приводятся все пять степеней семерки, три промежуточных и одна окончательная суммы. Посвященный в тайны арифметического счета должен был уметь составлять таблицы типа табл. 7, в которой все хорошо видно без всяких пояснений.

Таблица 7

1	7	49	343	2401	2801
2	14	98	686	4802	5602
4	28	196	1372	9604	11204
7	49	343	2401	16807	19607

Выделенные числа фигурировали в тексте задачи, невыделенные числа учащийся должен был уметь воспроизвести самостоятельно. В последней строке табл. 7 приведены степени числа 7, а в последнем столбце — промежуточные и окончательные суммы. Используемый древним математиком алгоритм счета, очевидно, тот же самый, что и в рассмотренной задаче 32, т.е. бинарный.

Но вот совпадение: в «Книге абака» средневекового математика Леонарда Пизанского (XII – XIII вв.), т.е. не безызвестного нам Фибоначчи, имеется «задача о 7 старухах, направляющихся в Рим, у каждой из которых по 7 мулов, на каждом из которых по 7 мешков, в каждом из которых по 7 хлебов, при каждом из которых по 7 ножей, каждый из которых в 7 ножнах».

Если в древнеегипетском папирусе суммируется пять степеней семерки, у Леонарда Пизанского — шесть, то в рукописях древней Руси встречается задача на суммирование уже семи степеней семерки; вот ее содержание: «Идет семь баб, у каждой бабы по семи посохов, на каждом посохе по семи сучков, на каждом сучке по семи кошелей, в каждом кошеле по семи пирогов, в каждом пироге по семи воробьев, во всяком воробье по семи пупков».

Надо ли говорить, что мы имеем дело со случайным совпадением задач на базе числа 7. Если бы какому-нибудь автору понадобилась задача на прогрессию, причем именно на базе числа 7, он вряд ли бы стал подменять содержание исходного текста. Нет никакого сомнения, что все три приведенные здесь задачи возникли независимо друг от друга. Эти задачи на числовые ряды умели решать во всех центрах цивилизации.

Приведем еще одну задачу на ряды из египетского папируса, которая говорит нам о том, как в заданных долях разделить некоторое количество ячменя между 10 лицами. «Средняя доля есть 1 мера. Вычти 1 из 10. Остаток есть 9. Составь половину разницы. Это есть 1/16. Возьми ее 9 раз. Это даст 1/2 + 1/16. Приложи это к средней доле. Вычитай для каждого лица по 1/8 меры, пока не достигнешь конца». Если число людей обозначить через n, количество мер ячменя — через S, разность — через d, то алгоритм сводится к вычислению следующих величин:

S/n, n – 1, d/2, d/2(n – 1), d/2(n – 1) + S/n.

Последняя величина есть первый член убывающей арифметической прогрессии, равный 25/16. Путем последовательного вычитания 1/8 из последнего числа, получаем ряд из девяти дробей: 23/16, 21/16, 19/16, 17/16, 15/16, 13/16, 11/16, 9/16, 7/16. В сумме с первым членом ряд дает 10 исходных мер ячменя.

Подобные задачи, кажется, не были известны европейским математикам начала эпохи Возрождения (по крайней мере, большинству из них), и они вынуждены были самостоятельно искать алгоритмы их решения. Такое происходило множество раз: какие-то ответы кем-то находились, но потом они терялись. Поэтому одну и ту же истину приходилось открывать в различных частях света и в разное время не единожды. Не исключено также, что в результате какого-нибудь катаклизма все знания современной цивилизации будут утрачены, однако какое-то число разумных людей останется жить на земле. Можно не сомневаться, что они сумеют переоткрыть для себя и теорему Пифагора, и формулу суммы членов ряда арифметической прогрессии, и многое другое, чем мы сейчас пользуемся. Первоначально эти знания будут носить исключительно конструктивный характер, как это было у древних народов, населяющих землю; затем произойдет формализация и омертвление этих конструктивных знаний, как мы можем наблюдать сегодня.