Конструктивная математика

Акимов О.Е.

10. Реконструкция математического мышления древних

Логика не только не добавляет математической строгости, но делает абсолютно невидимыми многие ранее вполне прозрачные геометрические построения. Сегодня стоит больших интеллектуальных трудов восстановить ту нехитрую цепь представлений, которыми пользовались древние вавилоняне и египтяне в массовом порядке. Нынешние историки науки не могут разгадать того, что не разъяснялось даже самым нерадивым школьникам — до того это были самоочевидные вещи. Вот один из длинной цепи примеров. Ван-дер-Варденом детально рассматриваются предложения II.9 и II.10 «Начал» Евклида, для чего он формулирует их в геометрической форме следующим образом: «II.9. Если прямая линия разделена на равные и неравные части, то квадраты на неравных частях, вместе взятые, вдвое больше квадратов на половине прямой и на отрезке между точками деления, взятыми вместе. II.10. Если прямая линия разделена пополам и к ней по прямой добавлен отрезок, то квадрат на всей линии вместе с добавленным отрезком, взятый вместе с квадратом на добавленном отрезке, будет вдвое больше квадрата на половине прямой вместе с квадратом на прямой, состоящей из половины первоначальной прямой и добавленного отрезка. Оба предложения, — пишет Ван-дер-Варден, — приводят к формуле:

» [14, c, 172].

Далее в его книге говорится, что эти предложения могут рассматриваться как решения задач, которые можно найти на вавилонских глиняных табличках, что, по мнению автора, доказывает факт «списывания» греками условий и решений задач вавилонян. Ван-дер-Варден утверждает, что задача, соответствующая предложению II.9, гласит: даны x + y = S, x² + y² = F, требуется найти x и y. Решая современными алгебраическими средствами эту систему из нелинейных уравнений, находим:

,    .

Задача, отвечающая предложению II.10, гласит: даны x – y = d, x² + y² = F, требуется отыскать те же x и y. Для них современные формулы выглядят так:

,     .

По поводу «плагиата» мы уже поговорили ранее, но у читателя, естественно, возникает другой вопрос: как древние вавилоняне могли находить значения x и y, не располагая современными алгебраическими методами? Ван-дер-Варден мимоходом заметил, что x и y можно найти, если «искусно применять теорему Пифагора», однако он не дал отчетливую реконструкцию решения подобных задач. 

В другом месте он пишет: «Вавилоняне мыслили, прежде всего, алгебраически. Сквозь геометрическую внешность просвечивает алгебраическая сущность». В своих исследованиях Ван-дер-Варден опирался на результаты Нейгебауера, который также считал вавилонян первоклассными алгебраистами: их «математика имеет сильно выраженную алгебраическую ориентацию», «вычисление ведется с величайшим изяществом и совершенно тем же методом, который применили бы и мы теперь» [13, c. 201]. 

Антропологи Люсьен Леви-Брюль и Карл Юнг считали древних по сравнению с нынешними умственно неполноценными людьми, Ван-дер-Варден и Нейгебауер впали в другую крайность — объявили их провидцами современных алгебраических формул, которые они получали, только вот не умели выразить их клинописью на глине. По этому поводу Лурье замечает: «От сложности применяемых Нейгебауером алгебраических формул рябит в глазах. По его мнению, вавилоняне применяли вполне сознательно хитроумный, алгебраический прием». В самом деле, как можно было решать задачи, приводящие к сложнейшим системам уравнений? Например, к таким: xy = 600,

Другой исследователь советского периода, А.А. Вайман, думал иначе, что «древние математики достаточно хорошо владели методом логического доказательства математических истин» [15, c. 209]. Значит, дело не в алгебре, а в логике? Но мы уже знаем, что это за инструмент и какая от него польза. Он приводит условие и решение задачи, которая похожа на задачи, сформулированные Ван-дер-Варденом. Вот ее условие: дана длина x и ширина y прямоугольного поля, причем x превышает y на d. Известна также площадь поля S; требуется найти стороны x и y.

Как он ни хвалит логику, но решает систему двух уравнений (xy = S, x – y = d) современным алгебраическим способом:

x = t + d/2,     y = t – d/2,     xy = t² – (d/2)², 

t² = (d/2)² + S,         t = ;

в результате получилась знакомая нам формула:

.

Записав эту формулу, Вайман не смог ответить на главный для любого историка вопрос, как пришли к ней древние математики. Следовательно, нужно продолжать искать разумную, скорее всего, геометрическую интерпретацию этой и других, подобных ей алгебраических формул.

Прежде всего, необходимо обратить внимание на то, что древние математики все величины выражали в конкретных числах, а числам ставили в соответствие либо отрезки длины, либо площади, либо объемы. В частности, задача, которую решал Вайман в общем виде, в действительности формулируется на конкретных числах: «Условие: длина и ширина; длина превышает ширину на 4, площадь 32, узнай длину и ширину. Решение: 4 раздели пополам, получишь 2; 2 умножь на само себя, ты увидишь площадь 4; площади 32 и 4 сложи, ты увидишь 36; узнай корень квадратный из 36, ты увидишь 6; сложи 6 и 2, ты видишь 8 — это длина; от 6 отними 2, ты увидишь 4 — это ширина». 

Хотя данный алгоритм и повторяет алгебраические формулы Ваймана, древний математик, чтобы прийти к нужному для себя результату, вряд ли манипулировал только буквенными символами. Алгеброй и логикой в том объеме, который здесь явно или неявно предполагают современные исследователи, древние математики, конечно, не владели. Их единственным инструментом могла быть геометрия, т.е. ясный пространственный образ, подвергавшийся каким-то не очень сложным действиям. 

Разумную реконструкцию решения подобных задач предлагает В.М. Розин. Он высказал предположение, что вавилоняне, скорее всего, просто умели прекрасно пользоваться пространственным воображением. Взяв за основу другие числа, он предложил следующую реконструкция решения задачи. 

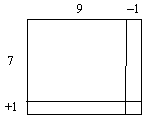
Пусть дано «прямоугольное поле: ширина 7, длина 9. От поля отрезали вертикальный участок со стороной 1 (рис. 4) и добавили горизонтальный участок со стороной 1. Какова величина исходного поля и разница между полями? 

Решение:

1) 7 · 9 = 63 — площадь исходного поля,
2) 7 + 1 = 8, 9 – 1 = 8 — нахождение сторон нового поля,
3). 8 · 8 = 64 — площадь нового поля,
4). 64 – 63 = 1 — разница между полями».

Рис. 4

Эти простые геометрические и арифметические действия древний математик производить мог и, видимо, производил. «Рассматривая решения этих задач, можно заметить, что новое поле, возникшее после передела, — квадратное (8 · 8). Кроме того, разница между полями, равная единице, совпадает по величине с маленьким квадратным полем (1 · 1), получившимся в правом нижнем углу чертежа (рис. 4). Наконец, длина и ширина исходного поля и нового поля связаны следующими соотношениями: ширина исходного поля меньше стороны нового квадратного поля на 1, а длина этого поля больше этой стороны на 1, разница же между длиной и шириной исходного поля (9 – 7 = 2) ровно в два раза больше стороны маленького квадратного поля (1). Отсюда при желании можно извлечь и план решения.

Известна величина исходного поля. Каким образом его нужно переделать, чтобы возникло новое квадратное поле? К исходному полю нужно добавить маленькое квадратное поле, сторона которого в два раза меньше разницы между длиной и шириной исходного поля. Затем нужно узнать сторону получившегося квадратного поля (т.е. извлечь корень квадратный из величины этого поля) и добавить (отнять) от этой стороны половину разности между длиной и шириной исходного поля» [16, c. 99].

Нам кажется, что Розин предложил правдоподобный выход из возникшей эпистемологической проблемы. Несомненно, все дело в умении древних математиков думать пространственными представлениями, а не алгебраическими или логическими понятиями, т.е. они превосходно манипулировали образами, а не символами. 

Аналогичным путем, видимо, решали задачи и египтяне, жившие в эпоху Среднего царства (2052—1786 гг. до Р.Х.). Вполне очевидные мысленные операция геометрического и логического характера древние математики не стремились вытаскивать на свет в форме занудных геометрических доказательств или логических умозаключений. Всё это софистико-схоластическое буквоедство возникло в эпоху Поздней Античности, когда оформилась субординация ученик — учитель, и особенно зацвело пышным цветом в Средние века, когда в Европе появились университеты.

Задачи типа «аха», которые решались методом ложного положения, или задачи на арифметические и геометрические прогрессии, которые мы уже затрагивали, не апеллируют к пространственным образам. Но подобных задач очень много в древнеегипетских папирусах. В связи с этим сложилась ложное мнение, будто на берегах Тигра и Евфрата, а также Нила, не умели решать задачи геометрического характера. Однако то, что вавилоняне и египтяне в противоположность грекам не часто прибегали к чертежам, еще не говорит об их незнании геометрии. Розин продемонстрировал нам, что вавилоняне, скорее всего, прекрасно владели геометрическими методами, причем настолько остроумными, что смогли поставить в тупик многих наших современных историков науки, приученных думать алгебраической символикой. Далее мы проиллюстрируем, что и египетские математики тоже весьма виртуозно владели геометрией, причем вовсе не считали нужным, как это делали греки, выставлять напоказ свое умение. 

Известна не одна задача, где для вычисления площади круга (S = π²d²/4) использовалась удивительно точная формула: S = d² (8/9)². По этой формуле выходит, что π = 3,1605, в то время как даже в Древнем Вавилоне принималось величина π = 3. Анна Раик [17, c. 36 – 37] выдвинула любопытную гипотезу, которая является, скорее всего, истинной. Она предположила, что площади круга диаметром d ставится в соответствие описанный квадрат A₀, из которого вычтены четыре площади A₁ малых квадратов со сторонами d/6 и восемь площадей A₂ со стороной d/9 (пояснения на рис. 5). В этом случае последовательные приближения давали следующие значения площади круга:

нулевое приближение — S₀ = A₀ = d²,
первое приближение — S₁ = S₀ – 4A₁ = d²(1 – 4/6²) = d²(8/9),
второе приближение — S₂ = S₁ – 8A₂ = d²(8/9 – 8/9²) = d²(8/9)²,

Рис. 5

Этот алгоритм выглядит достаточно правдоподобно, ведь нужно же было как-то формулу выводить, а учитывая любовь египтян к дробям, такой способ вывода вполне вероятен. Если бы практические нужды требовали более точного расчета площади круга, то древний математик ввел бы следующее приближение — в этом можно не сомневаться. Верно, что египтяне почти не оставили нам геометрических чертежей, однако не следует думать, что они вообще не прибегали к геометрическим представлениям. Известна одна задача, в которой в явном виде довольно детально произведен геометрический анализ, сопровождавшийся чертежом. Наш соотечественник, блестящий исследователь Юрий Яковлевич Перепелкин (1903—1982) выполнил иероглифический перевод содержания задачи 14 Московского папируса (о нём читайте в разделе Жизнь и труды Юрия Яковлевича Перепелкина ).

Эта задача включала схематический рисунок (рис. 6), позволяющий нам сориентироваться в отношении того, каким образом древнеегипетские математики обращались с пространственными формами. Содержание задачи сводится к примеру вычисления объема (V) усеченной пирамиды с квадратным основанием, когда высота (h) и стороны нижнего (a) и верхнего (b) квадратов заданы в конкретных числах. Алгоритм можно передать следующими словами:

"Если тебе дана пирамида без вершины в 6 локтей в высоту, в 4 локтя по нижней стороне и в 2 локтя по верхней стороне, то вычисления начни с нижней стороны, которую возведи в квадрат, получишь 16. Затем умножь 4 на 2, получишь 8; далее возьми 2 и возведи в квадрат, получишь 4; сложи вместе три числа — 16, 8 и 4, получишь 28; возьми треть от 6, получишь 2; перемножь эту 2 с числом 28, получишь 56. Ты нашел верно".

Рис. 6

Как видим, автор этого алгоритма рекомендует последовательно придерживаться школьной формулы вычисления, а именно: 

(а) V = (a² + ab + b²)h/3.

Схема (рис. 6), которой была снабжена задача, в лаконичной форме дублировала подробный алгоритмический текст задачи. Напомним, что все записанные на ней числа и действия с ними нужно прочитывать справа налево. На схеме, помимо известного нам иероглифа «результат», имеются еще два — «шагающие ноги», символизирующие математические действия сложение и возведение в квадрат (что также сводится к сложению). Иероглиф «шагающие ноги» можно было бы передать английским словом «go», который на русский язык переводится не только как «иди», но и более широко — «действуй». «Рот, откусывающий часть от целого» (в нашем случае «откусывается» треть от шести, т.е. две единицы), символизирует дробную часть.

Самое первое стоящее над пирамидой число указывает сторону верхнего сечения и тут же оно возводится в квадрат (возможно, автор желал тем самым показать, что рассматривается именно объемная фигура, а не плоская трапеция, как это может показаться на первый взгляд). Под нижним основанием пирамиды стоит четверка, указывающая сторону еще одного квадрата. Внутри пирамиды написаны два числа: первое 6, которое указывает высоту пирамиды, второе 56 — объем пирамиды. На одной строке с числом 6 автор записал математическое действие — «откусывание одной трети от шести» — и тут же помещен результат этого действия — 2. Слева от изображения пирамиды записано бинарное перемножение двух чисел — 28 · 2 = 56. В самом низу рисунка показано, как получается число 28; оно получается путем сложения 16, 8 и 4.

В изложенной задаче, прежде всего, поражает формула (а), по которой следует алгоритм решения. Если отбросить экзотические предположения, связанные, например, с посещением страны древних пирамид инопланетными пришельцами, которые могли бы подсказать формулу, то всякий историк науки обязан попытаться воспроизвести ход мысли древних математиков. Понятно, что без моделирования пространственными формами выражение (а) не получить.

Существует два варианта рассуждений. Первый основывается на том факте, что в Московском папирусе как будто бы изображена прямоугольная усеченная пирамида. В этом случае можно произвести ее разрез на четыре части, как это показано на рис. 7а, высчитать объем каждой части и затем произвести сложение. Результирующая формула будет иметь вид: 

(б) V = b²h + b(a – b)h + (a – b)²h/3.

Рис. 7

Здесь нужно заметить, что формула для объема пирамиды общего вида была известна, видимо, с очень древних времен. Этот объем равен одной трети от произведения площади основания пирамиды на ее высоту. Во всяком случае, ее несложно найти эмпирическим путем, как это сделал, в частности, Демокрит. Он составлял из «атомов», т.е. маленьких кубиков, сначала пирамиду, а потом из тех же самых «атомов» и на том же основании прямую призму, которая всегда оказывалась на две трети ниже высоты пирамиды. Аналогичным методом пользовался Архимед, когда он подсчитывал площади криволинейных геометрических фигур: он их взвешивал, помещал в ванны с водой и по произведенным физическим действиям судил о геометрических свойствах этих фигур. Поэтому последнее слагаемое в выражении (б) не вызывает вопросов. Но они тут же появятся, если данное выражение сравнить с выражением (а). Почему алгоритм рассматриваемой задачи из папируса не выстроен сразу по формуле (б)? Ведь невозможно себе представить, чтобы древнеегипетские математики могли произвести сложные алгебраические преобразования от формулы (б) к формуле (а). Они оперировали только конкретными числами, и ни о каких буквенных преобразованиях не могли и подумать (хотя бы потому, что тогда не было самого алфавита).

Более правдоподобным вариантом рассуждения древних кажется второй. Усеченную пирамиду, вылепленную, например, из сырой глины (причем необязательно прямоугольной формы), можно было бы разрезать, как это показано на рис. 7б. Тогда формула объема, выраженная через сумму ее составляющих, будет выглядеть уже несколько ближе к алгоритмической формуле (а): 

(в) V = a²h/3 + b²h/3 + 2(ah/2)b/3.

Долгое обращение с конкретными числами не могло не привести внимательного человека к мысли о справедливости коммутативного и дистрибутивного законов: 

ab = ba,         ad + bd + cd = (a + b + c)d.

Это значит, что путь от формулы (в) к формуле (а) существовал и он носил явно конструктивный характер, без манипуляции пространственными образами здесь не обошлось. Египетских жрецов не заботили доказательства, они думали только о вычислении подтверждаемого практикой результата.

Теперь перенесемся на другой конец света — в древний Китай. Там за 1100 лет до Р.Х. умели строить прямоугольные треугольники. В «Математическом трактате чжоу-би», («Чжоу-би суань цзин», чжоу-би — шест для измерения солнечной тени, аналог греческого гномона), принадлежавшем каллиграфической кисти Шан Гао, говорилось о треугольнике со сторонами 3, 4 и 5 единиц длины, а Чень-цзы, живший в VI в. до Р.Х., сформулировал теорему Пифагора в общем виде. Без элементарных навыков в области геометрии вряд ли знаменитый китайский астроном Ши Шень мог в IV в. до Р.Х. составить первый дошедший до нас звездный каталог, включающий 809 звезд.

В «Цзю чжан суань шу» («Математика в девяти книгах»), где были собраны задачи китайских математиков, живших в первом тысячелетии до Р.Х., есть книга V, которая называется «Оценка работ». Здесь приводятся задачи, связанные с земляными и строительными работами, в частности, даются алгоритмы расчета выработки на одного человека (в зависимости от материала, климатических условий и времени года) по строительству каналов, стен и плотин, имеющих порой весьма сложную форму, а также по копанию ям и рвов различной конфигурации. Нас сейчас будут интересовать задачи, связанные с нахождением объемов сложных геометрических фигур, которые были обойдены даже греческими математиками. Вот содержание задачи 17. Имеется сянь-чу. Нижняя ширина 6 чи, верхняя ширина 1 чжан [ = 10 чи], глубина 3 чи, верхняя ширина 8 чи, глубины нет, длина 7 чи. Спрашивается, каков объем?» 

Алгоритм лаконичный: «Сложи три ширины, умножь на глубину, еще умножь на длину, разделив на 6, возьми 1 раз». «Сань-чу» — это многогранник неправильной формы, изображенный на рис. 8а. Согласно условию задачи, имеем: 

а = 6,     b = 10,     c = 8,     h = 3,     l = 7, 

алгоритм следует изящной формуле: 

V = (a + b + c)hl/6.

Рис. 8

Чтобы найти объем, нужно произвести рассечение фигуры «сань-чу» на три части, одна из которых будет прямой призмой высотой a и с прямоугольным треугольником в основании (катетами у него являются величины h и l); две другие части представляют собой две равновеликие пирамиды с высотой h, в основании лежит трапеция, у которой высота равна l, а стороны — (b – a)/2 и (c – a)/2. В этом случае объем первой части будет равен ahl/2, объем двух других частей — 

2{1/2[(b – a)/2 + (c – a)/2]hl/3}; 

при сложении этих величин получим формулу для V. Данная формула была переоткрыта французским математиком Андриеном Лежандром (1752—1833) в его классическом курсе «Начала геометрии» (кн. VI, предложение 20). 

Между тем древние китайцы рассматривали множество других геометрических тел, например тело «чу-мэн», которое изображено на рис. 8б; формула, по которой ищется объем чу-мэна, выглядит следующим образом: 

V = (2l₁ + l₂)ah/6.

На рис. 8в изображено тело «чу-тун», которое похоже на четырехугольную усеченную пирамиду, только у «чу-туна» боковые грани при своем продолжении не сходятся в одной точке. Объем этой фигуры равен: 

V = [(2a₁ + a₂)b₁ + (2a₂ + a₁)b₂]h/6.

Объемы тел, найденные в «Цзю чжан суань шу», нельзя получить случайным образом, путем манипуляции символами, как это делают формалисты. Следовательно, даже в очень отдаленные эпохи мышление китайца было достаточно конструктивным. Главным же здесь является то, что исходный сложный объект разлагался на сумму простых элементов. Важно понять, что только пространственные образы диктуют логику алгоритмов и вычислительные формулы, но никак не наоборот. Какой бы сложной ни была задача, ее решение всегда должно быть связано с большим или малым числом наглядных и понятных действий с пространственными образами. Это эпистемологическое положение верно как для математиков Северной Африки и Юго-Восточной Азии, так и для математиков, живущих в другой местности.