
Письмо Огюстена Френеля к Франсуа Араго
относительно влияния движения Земли на
некоторые оптические явленияПисьмо это, напечатанное в Ann. de chim. et de phys., т. IX, стр. 57, сентябрьская тетрадь 1818 г., явилось результатом размышлений Френеля над проблемой, поставленной перед ним Араго и связанной с влиянием движения тела на преломление в нём света, идущего от источника, не принимающего участия в движении. Араго подверг вопрос экспериментальному изучению. В его опытах исследовалось, меняется ли показатель преломления призмы для света от звезды благодаря движению Земли. Араго пришёл к выводу, что такого влияния нет. Опыты эти были выполнены в 1810 г. и тогда уже доложены в Академии. Но опубликованы они были гораздо позднее (Comptes Rendus, т. XXXVI, стр. 38, 1853).
5 сентября 1818 г. Френель писал своему брату Леонору: "... Я недавно сделал небольшую работу, которой я придаю некоторое значение. Предполагая, что Земля настолько пориста, что сообщает проникающему и окружающему её эфиру очень малую часть своей скорости, например, не превышающей одной сотой доли, я доказал, что можно было бы объяснить удовлетворительным образом не только аберрацию звёзд, но также и все другие сложные явления оптики, связанные с движением земного шара, и т. д.". (Стр. 516.)
Текст и примечания к нему взяты из книги
О. Френель. "Избранные труды по оптике" (серия: Классики естествознания). Перевод с французского З.А. Цейтаина, под редакцией акад. Г.С. Ландсберга. Государственное издательство Технико-теоретической литературы. Москва 1953 (с. 516-526, примечания с. 595-599)Мой дорогой друг,
Вашими прекрасными опытами, касающимися света звёзд, Вы показали, что движение земного шара не имеет никакого заметного влияния на преломление лучей, испускаемых этими светилами.
Нет возможности объяснить этот замечательный результат в рамках эмиссионной теории, если не предположить—как Вы на это указываете,—что светящиеся тела придают частицам света бесконечное количество различных скоростей и что эти частицы действуют на орган зрения только при одной из этих скоростей, по крайней мере, при скоростях, находящихся в очень близких границах друг от друга, так что отличие на одну десятитысячную в ту или иную сторону более, чем достаточно, чтобы воспрепятствовать получению ощущения света.
Необходимость этой гипотезы является одной из немалых трудностей эмиссионной теории. Действительно, чем же обусловлено зрение? Вызывается ли оно ударом световых частиц в зрительный нерв? Но этот удар не сделался бы нечувствительным в результате увеличения скорости. Не зависит ли оно от того, каким образом преломляются световые частицы в зрачке? Но, например, красные частицы, скорость которых уменьшена почти на пятидесятую часть, преломлялись бы ещё меньше, чем фиолетовые лучи, и тем не менее не вышли бы из спектра, который представляет собой пределы зрения.
Вы просили меня исследовать, не могут ли результаты этих наблюдений лучше быть согласованы с системой, согласно которой свет представляет собой колебания всепроникающей жидкости. Тем более необходимо дать объяснение с точки зрения этой теории, так как она в равной степени должна прилагаться к земным объектам; ибо скорость, с которой распространяются волны, не зависит от движения тела, которое их испускает.
Если предположить, что наш земной шар сообщает своё движение эфиру, которым он окружён, можно было бы легко понять, почему та же самая призма всегда преломляет свет одним и тем же образом, независимо от того, с какой стороны этот свет подходит. Однако, с точки зрения этой гипотезы, оказывается, по-видимому, невозможным объяснить явление аберрации звёзд: я, по крайней мере, до сих пор мог чётко понять это явление, только предполагая, что эфир свободно проходит через земной шар и что скорость, сообщённая этой тонкой жидкости, представляет собой только небольшую часть скорости Земли и не превышает, например, одной сотой доли этой скорости
[(Прим. О.А.) Аберрация открыта Брэдли в 1728 году в предположении, что свет, по Ньютону, представляет собой поток частиц, распространяющихся в полной пустоте. Если свет представлять в виде колебательных волн эфира, то возникают трудности ее понимания.
(Прим. 152 по цитируемой книге) Объяснение аберрации света с волновой точки зрения было впервые предложено Юнгом в 1804 г., принимавшим, что эфир не увлекается Землёй: «Я склонен считать, что светоносный эфир проникает в вещество всех материальных тел с очень малым или даже без всякого сопротивления, возможно так же легко, как ветер проходит сквозь рощу» (Phil. Trans., XCIV, стр. 1, 1804). (Стр. 517.) ]
Как бы странной ни показалась эта гипотеза с первого взгляда, она, как мне кажется, совершенно не противоречит идее, созданной наиболее великими физиками относительно чрезвычайной пористости тел.
Действительно, можно спросить, каким образом с одной стороны очень тонкое непрозрачное тело перехватывает свет, а с другой — образуется поток эфира через наш земной шар. Не претендуя исчерпывающим образом ответить на это возражение, я, тем не менее, замечу, что эти два вида движений слишком различаются по своей природе, чтобы можно было прилагать к одному то, что наблюдается относительно другого.
Световое движение является не течением, а колебанием эфира. Нетрудно понять, что маленькие элементарные волны, на которые разделяется свет, проходя через тела, могут в известных случаях оказаться несогласованными после того, как они соединятся, что может произойти вследствие разности пройденных ими путей, или неравных замедлений, которые они испытали во время своего прохождения. Это может помешать распространению колебаний, или изменить их природу таким образом, что будет устранена их способность освещать подобно тому, как это наблюдается весьма выразительным образом на чёрных телах; а между тем те же самые обстоятельства могут и не воспрепятствовать течению эфира.
Прозрачность минерала гидрофана увеличивают [153], смачивая его. Очевидно, что добавление воды между частицами, которое благоприятно действует на распространение световых колебаний, должно, напротив, становиться небольшим дополнительным препятствием для течения эфира, что хорошо доказывает большое различие, которое существует между этими двумя родами движений.
[(Прим. 153) Пример увеличения прозрачности пористых тел заимствован у Ньютона (Оптика, вторая книга, часть III, предл. III), Гидрофан — SiO2 с различным содержанием воды (см. примеч. 102а С. И. Вавилова в «Оптике»). Об опытах с увеличением прозрачности гидрофана и изменении его показателя преломления при смачивании упоминает и Араго (Oeuvres, т. 10, стр. 310). (Стр. 518.)]
Непрозрачность Земли, таким образом, не является достаточным основанием, чтобы отрицать существование течения эфира между её частицами, и можно предположить, что Земля настолько пориста, что она сообщает этой жидкости только очень небольшую долю своего движения.
При помощи этой гипотезы явление аберрации может быть столь же легко объяснено в волновой теории, как и в эмиссионной, ибо это явление оказывается результатом смещения зрительной трубы во время прохождения через неё света. Но согласно этой гипотезе световые волны не участвуют заметным образом в движении зрительной трубы, которую я полагаю направленной на истинное место нахождения звезды. Поэтому изображение этого светила окажется позади идти, помещённой в фокусе окуляра на таком расстоянии, которое равно тому, которое проходит Земля за время, пока свет проходит зрительную трубу [1б4].
[(Прим. 153) Такое объяснение аберрации О. Френель даёт ещё в письме к брату Леонору от 6/VII 1814 г. после обсуждения неясностей в истолковании этого явления, вызванных довольно путаным изложением корпускулярной теории аберрации, даваемым Айи в его учебнике, который служил в учебные годы Френеля основным пособием во французских школах…
(Прим. О.А.) Эмиссия (см. термин, выделенный выше курсивом) — это генерация световых частиц неким святящимся телом. Вместе с этим понятием в физике появляются проблемы. Если глазное яблоко наполняется какими-то частицами, то когда-то должно произойти его насыщение этими частицами. Почему глаз не лопается от наполнения его этими частицами — хотя бы к концу жизни? Куда деваются частицы, которые воздействуют на сетчатку глаза? Аналогичный вопрос можно задать и в отношении источника света: почему он не истощается?
Следующий вопрос: откуда все световые частицы в космосе и на Земли знают, с какой скоростью им лететь в пустом пространстве? Можно было бы ожидать, что частицы, вылетевшие с поверхности Солнца, будут иметь большую скорость, чем частицы, испущенные, например, газовой горелкой, зажженной в лаборатории . С открытием же таких явлений, как интерференция и дифракция, корпускулярная теория оказалась совершенно бессильной.
Отказ от эмиссионной теории в пользу эфирной был большим благом для науки. Однако объяснение аберрации лучей света, идущего от звезд к Земле, на основе волновой теории и наличия эфира неоднозначно. Здесь предполагается, по крайней мере, два варианта: либо полное увлечение эфирной среды поверхностью Земли, либо полная прозрачность пористого тела Земли для мировой жидкой или газовой среды. Заслуга Френеля как раз и состоит в том, что он нашел промежуточное решение, лежащее между этими двумя крайностями. Правда, и в его теории имеются некоторые шероховатости.
Дело в том, что вслед за Юнгом, по-видимому, по инерции мышления, Френель говорит о пористости тела Земли, т.е. предполагает существование двух субстратов — весомого вещества и практически невесомого эфира. Такое деление материи неизбежно ведет к логическому противоречию. Сколь бы малым ни было сопротивление эфира, оно рано или поздно скажется на снижении скорости движения Земли, а также других космических тел и не только космических.
Окончательное решение данной проблемы состоит в следующем. Вещественные тела, включая Землю, представляют собой сложные возбуждения эфира. Эти возбуждения способны двигаться в мировой среде подобно тому, как распространяются акустические волны в газе, жидкости или в твердых телах. Нет двух сортов материи, есть только эфир и его сгустки, имеющие большую плотность, чем невозбужденный эфир. Перемещаться могут только эти сгустки, сам же эфир — неподвижен для любых вещественных образований. Он вообще не захватывается вещественным телом.
Под частичным увлечением эфира нужно понимать захват системы сгустков или отдельных возбуждений мировой среды. Например, возбуждение эфира может представлять собой тор или вихревую трубку. В этом случае будет перемещаться геометрическая форма этого возбуждения, т.е. тор или трубка, но не сам эфир как некий субстрат.
Все эфирные возбуждения имеют единую электромагнитную природу. Гравитационные напряжения складываются из электромагнитных возбуждений, образуя свой, достаточно автономный уровень организации материи. В пределах Солнечной системы для гравитационных сил справедливы законы Кеплера и всемирный закон тяготения. Но в масштабах галактик начинают играть более общие закономерности. В частности, движение рукавов спиральных галактик уже не описывается законами Кеплера. Так называемые сильные и слабые взаимодействия тоже обязаны, прежде всего, электромагнитным возбуждениям. Но крохотные масштабы микромира накладывают на них свои особенности, так что законы Максвелла для них перестают работать.]
Теперь нужно объяснить, исходя из той же самой гипотезы, каким образом видимая рефракция не изменяется с изменением направления световых лучей по отношению к движению Земли.
Пусть EFG (рис. 42) — призма, сторона EF которой предполагается перпендикулярной одновременно и к плоскости эклиптики, и к падающим лучам. Таким образом, эти последние имеют направление движения Земли: если оно может оказывать влияние на преломление лучей, то в рассматриваемом случае это влияние должно быть наиболее заметным.
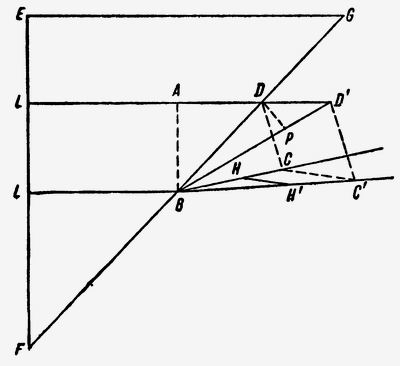
Рис. 42Я предполагаю, что лучи движутся в том же самом направлении, как и призма.
Поскольку лучи, будучи перпендикулярными к входной плоскости, не испытывают никакого преломления на этой стороне призмы, нам достаточно рассматривать только эффект, оказываемый второй поверхностью. Пусть LD и LB будут двумя из лучей, которые встречаются выходной поверхностью в точках D и В, Пусть ВС будет направлением, которое принимает луч LB, выходя из призмы в том случае, когда призма неподвижна. Если из точки D опустить перпендикуляр на исходящий луч, а из точки В провести линию ВА перпендикулярно к падающим лучам, то свет должен пройти расстояние AD за тот же промежуток времени, как и расстояние ВС: таков закон, который определяет направление преломлённой волны DC. Но поскольку призма увлекается движением Земли, то за время, пока свет проходит отрезок AD, точка D смещается; а это, увеличивая разность путей, пройденных в стекле двумя лучами LD и LB, должно изменить угол преломления. Пусть FG представляет собой положение выходной поверхности призмы в тот момент, когда падающая волна прибыла в АВ, a D' будет той точкой, где луч AD достигает этой поверхности и выходит из призмы. Пусть ВС' будет новым направлением преломлённых лучей. Перпендикуляр D'C' будет фронтом исходящей волны, который должен удовлетворять общему условию, что AD' должно быть пройдено светом за тот же промежуток времени, что и ВС'. Но для того чтобы определить отношения длин этих двух интервалов, нужно рассчитать то изменение, которое движение призмы привносит в скорость проходящих через неё световых волн.
Если бы эта призма увлекала с собой весь содержащийся в ней эфир, т. е. если бы, таким образом, вся среда, которая служит передатчиком волн, участвовала бы в движении Земли, то скорость световых волн была бы той скоростью, которую они должны были бы иметь в этой среде, предполагаемой неподвижной, увеличенною на скорость движения Земли. Но случай, о котором идёт речь, является более сложным. Нашим земным шаром увлекается только некоторая часть этой среды, а именно та, которая образует собой превышение его плотности по сравнению с окружающим эфиром. Аналогия указывает, что, когда смещается только часть среды, то скорость распространения волн должна увеличиться только на скорость центра тяжести системы [155].
[(Прим. 155) Вывод коэффициента увлечения в теории Френеля может быть выполнен следующим образом. Увлекаемая часть составляет превышение плотности эфира в среде (Δ') над плотностью окружающего эфира (Δ), т. е. равна (Δ' – Δ), причём Δ'/Δ = μ², где μ — показатель преломления. Назовём координату, характеризующую положение неувлскаемой части, через х1 (так что dх1 = 0); координату увлекаемой части — через х2 (так что dх2 = 0); если скорость тела (а следовательно, и избыточной части эфира) есть w, a dt — время. Приращение координаты центра тяжести эфира (х) за это же время есть dx, и его можно вычислить из известного соотношения
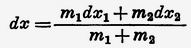
где m1 — масса неувлекаемой и m2 — масса увлекаемой части эфира в теле, объём которого есть V.
Итак,
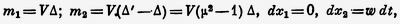
т. е.
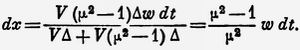
Или скорость центра тяжести эфира (скорость увлечения) есть
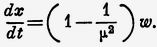
Таким образом, коэффициент увлечения κ = 1 – 1/μ².
Много лет спустя Стокс вывел (Phil. Mag. XXVIII, стр. 76, 1846) коэффициент увлечения из условия сплошности эфира, уплотняемого при вхождении в движущееся тело и разрежаемого при выходе из него. Это условие даёт: Δ · w = Δ' · w', где w' — скорость эфира по отношению к телу. Таким образом, скорость эфира, переносимого вместе с телом, по отношению к внешнему эфиру (скорость увлечения) есть
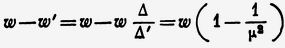
Непосредственное опытное подтверждение формулы увлечения Френеля было получено в 1851 (С. R., 33, стр. 349 (1851)) с помощью интерференционных опытов Физо (Fizeau Hyppolyte, 1819 — 1896). Эти опыты в улучшенном виде были повторены А. Майкельсоном (Michelson Albert, 1852 — 1931) совместно с Морли (Amer. Journ. of Science 31, стр. 377 (1886)) и П. Зееманом (Zeeman Piter, 1865 — 1943) (Ргос. of Amsterd. Acad. 17, стр. 445, 1914 и 18, стр. 398, 1915). (Стр. 521.) ]
Этот принцип очевиден для случая, когда часть, находящаяся в движении, представляет собой половину среды; ибо, относя движение системы к его центру тяжести, который мы на один момент представляем неподвижным, эти две половины удаляются от него с равными скоростями, но в противоположных направлениях. Отсюда вытекает, что волны должны в одном направлении быть замедлены настолько же, насколько они ускоряются в другом направлении, и что они обладают только обычной скоростью распространения по отношению к центру тяжести или, что то же самое, что они разделяют его движение. Если бы движущаяся часть представляла собой четвертую, восьмую, шестнадцатую и т. д. долю среды, можно было бы также легко доказать, что скорость, которая должна быть добавлена к скорости распространения волн, является одной четвертью, одной восьмой, одной шестнадцатой и т. д. скорости подвижной части, или, иначе, скоростью самого центра тяжести; отсюда ясно, что теорема, будучи правильной для этих частных случаев, должна быть правильной и вообще.
Установив это и принимая [156], что упругость в призматической среде равна упругости в окружающем её эфире (для большей простоты я предполагаю, что опыт производится в пустоте), можно рассматривать замедление света в неподвижной призме, как обусловленное только большей плотностью среды. Это даёт способ определения отношения плотностей двух сред, так как известно, что это отношение обратно пропорционально отношению квадратов скоростей распространения волн.
[(Прим. 156) Здесь, как и в своих более поздних работах (см. № VII и IX), Френель исходит из допущения, что оптическое различие всех сред, состоит в различии в плотностях при равенстве упругостей заключённого в них эфира. См., впрочем, «Дополнительное замечание к этому письму». (Стр. 521.)]
Пусть d и d' являются длинами волн света в эфире, окружающем призму, и в самой призме; Δ и Δ ' — плотности этих двух сред; отсюда, следовательно, имеем пропорцию
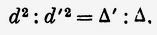
откуда
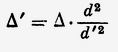
и, следовательно,
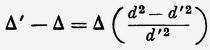
Такова плотность движущейся части среды призмы. Если обозначить через t пространство, которое пробегает Земля за время одного светового колебания, то смещение центра тяжести этой среды за тот же период времени, которое я принимаю за единицу, или, иначе говоря, скорость этого центра тяжести будет
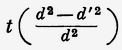
Из этого вытекает, что длина волны d" в призме, уносимой вместе с земным шаром, будет равна
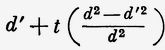
Рассчитывая при помощи этого выражения расстояние AD' (рис. 42), которое проходится лучом AD до его выхода из призмы, можно легко определить направление преломлённого луча ВС'. Если его сравнить с направлением того же луча ВС в том случае, когда призма неподвижна, мы получаем для синуса угла СВС', пренебрегая по причине малости t всеми членами, умноженными на его квадрат и высшие степени, выражение
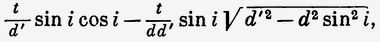
где i представляет собой угол падения ABD.
Я предполагаю, что через какую-нибудь точку H луча ВС проводят линию НН', параллельную эклиптике и равную пространству, пройденному Землёй в течение времени, которое нужно свету для того, чтобы пройти от В в Н'; если оптическая ось зрительной трубы, при помощи которой наблюдают визирную точку, направлена по ВН', то свет для того, чтобы прибыть в Н' в то же время, как и нить трубы, увлекаемой движением Земли, должен следовать по направлению ВН'; но линия ВН' в точности совпадает с направлением ВС луча, преломлённого призмой, уносимой этим же самым движением, ибо для значения синуса НВН' мы также находим выражение
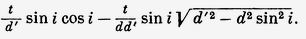
Таким образом, нужно поставить зрительную трубу в том же самом направлении, как и в том случае, если бы призма была неподвижной, откуда следует, что движение нашего земного шара не должно иметь никакого заметного влияния на видимое преломление в том случае, если предположить, что он сообщает эфиру только очень малую долю своей скорости [157]. При помощи очень простого расчёта можно убедиться, что также дело должно обстоять и при отражении. Таким образом, эта гипотеза, которая даёт удовлетворительное объяснение явлению аберрации, не приводит к каким-либо следствиям, которые противоречили бы наблюдаемым фактам.
[(Прим. 157) Вычисления, опущенные Френелем, могут быть выполнены несколько более простым способом, подобным указанному в книге Е. Whittaker, A History of the Theory of Aether and Electricity, London, 1951.
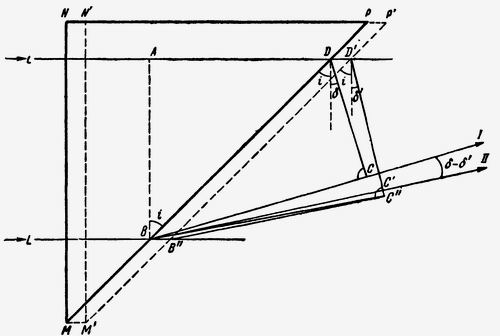
Рис. 55Для этого дополним чертёж (рис. 42), как показано на рис. 55, M'N'P' — положение приемы MNP через время τ, после того как фронт света достиг положения АВ и в точке В покинул призму (i — угол падения). Если бы призма была неподвижна, то фронт выходящей волны имел бы направление DC, повернувшись на угол δ. Если призма движется, то фронт выходящей волны займёт положение D'C' повернувшись на угол δ'. Угол между лучами I и II есть (δ – δ'). Дополним построение, продолжив LB до пересечения с P'M' в точке В". Опустим из В" перпендикуляр на продолжение фронта D'C' и основание этого перпендикуляра С" соединим с В. Легко видеть, что ВВ" ( = wτ) гораздо меньше ВС ( = cτ). Следовательно, угол при С" очень мал, и мы можем считать
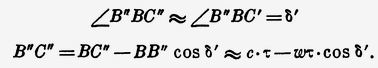
Из ΔB"D'C" имеем:
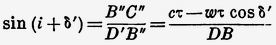
из ΔABD имеем:
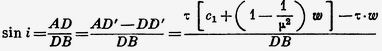
ибо AD' есть путь, проходимый светом за время τ внутри движущегося стекла, т. е. со скоростью, равной
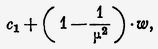
где c1 = c/μ — скорость в покоящемся стекле, а (1 – 1/μ²) — коэффициент увлечения (μ — показатель преломления стекла).
Итак,
(I)
с точностью до w²/c².
Если w = 0 (призма неподвижна), то δ = δ', т. е.
(II)
что можно видеть и непосредственно из ΔBDC и ΔBDA. Вычитая (I) из (II), найдём:
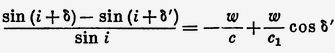
Так как δ – δ' очень мало, то последнее соотношение без труда преобразуется (принимая во внимание, что
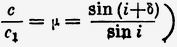
к следующему виду:
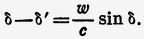
Таким образом, угол δ – δ' равен углу
Но последний есть угол аберрации для телескопа, направленного вдоль луча I, ибо направлени скорости w составляет с лучом I угол СВВ"= δ.
Итак, наблюдая звезду через призму, мы видим её в том направлении, в которое она кажется смещённой благодаря аберрации, изменённом на угол преломления, обусловленный покоящейся призмой. Другими словами, движение Земли не влияет с точностью до величины второго порядка на преломление света, идущего от звёзд. (Стр. 523.) ]
Я закончу это письмо применением этой же самой теории к опыту, предложенному Бошковичем [158], состоящему в том, чтобы наблюдать явление аберрации, при помощи труб, наполненных водой, или другой жидкостью, обладающей значительно большим преломлением, чем воздух, для того чтобы убедиться, не меняется ли направление, в котором наблюдается звезда вследствие того изменения, которое вносится жидкостью в путь света [159].
[(Прим. 158) Бошкович (Boscowich Rogerio, 1711—1787), горячий сторонник идей Ньютона, начавший их пропаганду в Италии, развивавший представление о действии на расстоянии как между атомами вещества, так и между веществом и световыми корпускулами. Его важнейшие сочинения: Theoria Philosophiae Naturalis, Venice, 1763; Dissertatio de lumine, 1766 и др. (Стр. 523.).
(Прим. 159) Аберрационный опыт с трубой, наполненной водой, был выполнен в 1871 г. Эйри (Airy, G. В., 1801 – 1892) (Ргос. Roy. Soc, XX, стр. 35, 1871) и подтвердил, в согласии с заключением Френеля, что угол аберрации остаётся таким же, как и при пустой трубе. (Стр. 523.) ]
Я замечу, прежде всего, что бесполезно осложнять аберрацией искомый результат и что можно его определить так же хорошо, нацеливаясь на любой земной объект, как и на звезду. Вот наиболее простой и удобный, как мне кажется, способ производства этого опыта.
Укрепив к самой зрительной трубе или лучше к микроскопу FBDE (рис. 43) миру М, расположенную на продолжении оптической оси СА, направляют эту систему перпендикулярно эклиптике и после производства наблюдения в одном направлении всю систему поворачивают в обратную сторону и делают наблюдение в противоположном направлении. Если бы земное движение смещало изображение точки М по отношению к нити окуляра, то и это изображение было бы видимо при этом способе то справа, то слева от нити.
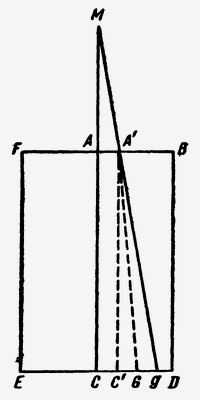
Рис. 43В эмиссионной системе, как это уже отметил Вильсон, очевидно, движение Земли ничего не должно изменить во внешнем виде этого явления. Действительно, благодаря этому движению луч, исходящий из М, должен принять для того, чтобы пройти через центр объектива, направление МА', такое, чтобы пространство АА' было пройдено земным шаром за тот же промежуток времени, который требуется свету для того, чтобы пройти расстояние МА' или МА (вследствие малости скорости Земли сравнительно со скоростью света). Обозначая через v скорость света в воздухе и через t скорость Земли, мы получаем
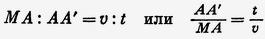
это синус угла падения. Если v' — скорость света в более плотной среде, которая находится в трубе, то синус угла преломления С'A'G будет равен t/v'; следовательно, мы будем иметь C'G = A'C'( t/v'), откуда получаем пропорцию C'G : A'C' = t : v' . Следовательно, нить С' окуляра, помещённая на оптической оси трубы, прибудет в G в то же время, как и световой луч, прошедший через центр объектива. Волновая теория приводит к тому же результату [160].
[(Прим. 160) Причины, приводящие к тому, что в случае совместного движения источника и трубы направление света от источника, находящегося на оси, образует с осью угол, отличный от нуля, различны для корпускулярной и волновой теории. Для корпускулы (или волны при допущении увлекаемого эфира) скорость света, идущего от миры, складывается из скорости света от неподвижной миры и скорости переносного движения. Для волны, при допущении неувлекаемого эфира, фронт волны от источника, лежащего на оси трубы, подходит к трубе наклонно, так что нормаль к фронту составляет с осью угол, равный t/ d, где t — скорость переносного движения, a d — скорость света.
Небезынтересно отметить, что хотя вопрос о наблюдении источника, движущегося совместно с трубой, был всесторонне рассмотрен Френелем в 1818 г., Бухерер через сто с лишним лет (Zeits. f. Phys. 41, стр. 18, 1927) выступил с ошибочным предложением использовать подобный опыт для экспериментального решения вопроса об увлечении эфира (см. С. И. Вавилов, экспериментальные основания теории относительности, Москва – Ленинград, 1928, гл. I, стр. 28). (Стр. 525.) ]
Для большей простоты я предполагаю, что микроскоп расположен в пустоте. d и d' — скорости света в пустоте и в среде, которую содержит труба; для синуса угла падения AMА' мы находим величину t/d, а для синуса угла преломления СA'G величину td'/d².
Таким образом, независимо от смещения волн в направлении движения Земли C'G = A'C' (td'/d²) .
Но скорость, с которой эти волны увлекаются движущейся частью среды, в которой они распространяются, равна
;
следовательно, их общее смещение Gg за время, которое они тратят для прохождения трубы, равно
,
и значит,
.
Таким образом, мы имеем пропорцию C'g : А'С'= t : d'. Следовательно, изображение точки М прибудет в точку g в то же время, как и нить микрометра.
Стало быть, вид явления всегда должен остаться одним и тем же, каково бы ни было направление, в котором мы повернули бы этот инструмент. Хотя этот опыт ещё никогда не производился [Эти строки Френель пишет в 1818 году; еще раз напомним, такой опыт осуществил Физо в 1851 году], но я нисколько не сомневаюсь, что его проведение подтвердит вывод, к которому мы приходим, равным образом, исходя как из эмиссионной теории, так и из волновой.
Дополнительное замечание к этому письму
(Ноябрьская тетрадь 1818 г.)Рассчитывая преломление света в призме, увлекаемой движением Земли, я предположил для упрощения своих рассуждений, что разность между скоростями света в призме и в окружающем эфире происходит исключительно из разности в плотности, считая, что упругость остаётся той же самой как в той, так и в другой среде; но вполне возможно, что эти две среды различаются по своей упругости так же, как и по плотности. Считается даже, что упругость твёрдого тела может изменяться с направлением, следуя которому его рассматривают; и это весьма вероятно является той причиной, которая вызывает двойное преломление в том виде, в каком это явление наблюдал д-р Юнг. Но какова бы ни была гипотеза, которую мы выскажем относительно причин замедления прохождения света в прозрачных телах, можно всегда для разрешения предложенной мне проблемы подставить мысленно вместо реальной среды призмы упругую жидкость, напряжение упругости которой находится в равновесии с упругостью окружающего её эфира и обладающую такой плотностью, что скорость света будет в точности одинаковой в этой жидкости и в призме, которые мы предполагаем находящимися в покое; это равенство должно продолжать существовать также и в этих двух средах, увлекаемых движением Земли: таковы те основания, на которых зиждется мой расчёт.
Материал сверстал и разместил в Сети Олег Акимов 21 февраля 2014 года