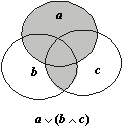Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

1.3. Методы доказательства в логике Буля

Аксиоматический и конструктивный способы обоснования

Как было сказано, в логике широко используются два подхода — аксиоматический и конструктивный. При аксиоматическом доказательстве используется жесткая система аксиом, состоящая, например, из четырех только что названных. Все остальные тождества необходимо представлять через эти законы. При конструктивном же доказательстве можно воспользоваться системой конструктов, примерами которых являются диаграмма Эйлера — Венна и таблица истинности. Продемонстрируем различие этих двух подходов.

Для доказательства простого тождества (а ∧ 0 = 0) приверженец аксиоматического подхода приведет примерно такую цепочку преобразований:

а ∧ 0 = а ∧ (a ∧ а) = (а ∧ a) ∧ а =

= ((а ∧ a) ∨ 0) ∧ а = ((а ∧ a) ∨ (a ∧ а)) ∧ а =

= (а ∧ (a ∨ а)) ∧ а = (a ∧ 1) ∧ а = a ∧ а = 0.

И сделает он это только ради того, чтобы формально привязаться к провозглашенной выше системе аксиом. Для конструктивиста же исходное тождество практически не потребует никаких доказательств.

Картина выглядит противоположным образом в отношении, например, закона дистрибутивности. Аксиоматик в данном случае не предпримет никаких действий, а сторонник конструктивного подхода обязан продемонстрировать эквивалентность левой и правой частей тождества: 

а ∨ (b ∧ c) = (а ∨ b) ∧ (a ∨ c).

Проведем доказательство с помощью диаграмм Эйлера – Венна. Построим две диаграммы, изображенные на рис. 1.13, которые отвечают двум операциям левой части тождества.

       

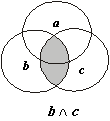
Рис. 1.13

Теперь построим еще три диаграммы (рис. 1.14), соответствующие трем операциям, фигурирующим в правой части закона дистрибутивности. Как видно из диаграмм, результаты построения логических операций левой и правой части закона дистрибутивности полностью совпали.

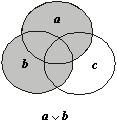
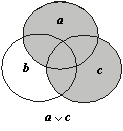
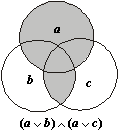
Рис. 1.14

Докажем с помощью диаграмм Эйлера – Венна справедливость более сложного тождества:

a + b + c + d = 

= ((a ~ b) → (c + d)) ∧ ((a + b) | (c + d)).

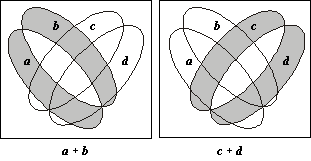
На рис. 1.15 изображены две операции — a + b и c + d, — фигурирующие в левой части приведенного тождества. Следует заметить, что диаграмма Эйлера – Венна, нарисованная с помощью кругов, для четырех переменных a, b, c и d не является полной, поскольку она содержит только 14 областей, а необходимо 16. Поэтому в роли исходных областей выбраны эллипсы.

Рис. 1.15

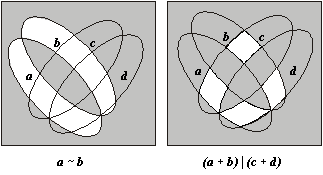
На рис. 1.16 изображены четыре диаграммы, соответствующие операциям правой части тождества; последняя из них является результирующей. Но точно такая же результирующая диаграмма получится при сложении по mod (2) двух первых диаграмм: 

(a + b) + (c + d).

Так как результирующие диаграммы левой и правой частей одинаковы, приведенное тождество верно.

Рис. 1.16

В правильности тождества можно убедиться с помощью таблицы истинности (табл. 1.17). Она показывает, что наборы значений из нулей и единиц для левой части ( f_L ) совпали с наборами правой части ( f_R ), значит исходное тождество верно. 

Таблица 1.17

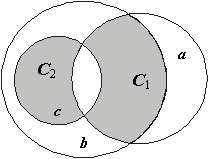
Рис. 1.17

Можно ставить обратную задачу, т.е. по известной диаграмме находить отвечающее ей компактное аналитическое выражение. Пусть дана диаграмма, изображенная на рис. 1.17. Найдем соответствующее ей аналитическое выражение. Для этого заштрихованные области представим в виде конституент:

С₁ = a ∧ b ∧ c,     С₂ = a ∧ b ∧ c.

Искомое выражение получается при объединении этих конституент:

х = С₁ ∨ С₂ = b ∧ ((а ∧ c ) ∨ (a ∧ c)) = b ∧ (а + c).