Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

1.3. Методы доказательства в логике Буля

Примеры доказательств булевых тождеств

Требуется выяснить, будет ли выполняться закон ассоциативности относительно штриха Шеффера:

(a | b) | c = a | (b | c)?

Здесь можно не прибегать к таблицам истинности или диаграммам Эйлера — Венна. Достаточно знать связь между операциями, чтобы показать, что закон не выполняется:

a | (b | c) = 1 + а (1 + bc) = 1 + а + abc;

(a | b) | c = 1 + (1 + ab) с = 1 + с + abc.

Позиция конструктивистов состоит в том, чтобы любое тождество в математической логике получило свое убедительное обоснование, будь то закон дистрибутивности для дизъюнкции и конъюнкции или закон ассоциативности для этих операций — ничто не должно браться в качестве «аксиом», т.е. утверждений без доказательств. Аналогичный конструктивный прием можно использовать для доказательства тавтологии:

(а ∧ а (а → b)) → b = 1.

Доказательство:

а (1 + а + аb) → b = аb → b = 1 + аb + аbb = 1.

В следующем примере полиномиальная форма уже не используется, а доказательство ведется посредством булевых операций. Требуется доказать:

((а + b) → (а ∨ b)) ∧ ((а ∨ b) → (а +b)) = a | b.

Доказательство:

((а + b) → (а ∨ b)) ∧ ((а ∨ b) → (а + b)) =

= (((а ∨ b) ∧ (а ∨ b)) → (а ∨ b)) ∧

∧ ((а ∨ b) ∨ ((а ∨ b) ∧ (а ∨ b)) =

= ((а ∧ b) ∨ (а ∨ b) ∨ (а ∨ b)) ∧ ((а ∨ b) ∨ (а ∨ b)) =

= 1 ∧ ((а ∧ b) ∨ (а ∨ b)) = а ∨ b = a | b.

Часто встречаются доказательства смешанного характера. Например, требуется установить, что

A ∪ В = 1, если A ⊂ В.

Когдa встречается символ включения, его лучше всего перевести в тождество. Если A полностью включено в В, то с помощью диаграмм Эйлерa — Веннa легко проверить, что 

A ∩ В = A или A ∪ В = В.

Далее, используя последнее равенство и аксиомы булевой логики, получим:

A ∪ В = A ∪ (A ∪ В) =

= (A ∪ A) ∪ В = 1 ∪ В = 1.

Предположим, требуется доказать тождество

A ∩ В = В или A ∪ В = А.

В данном случае доказательство можно провести, по крайней мере, двумя способами. Первый способ:

В = В ∪ 0 = В ∪ (A ∪ A) =

= (A ∪ В) ∩ (A ∪ В) = A ∩ (A ∪ В) =

= (A ∩ A) ∪ (A ∩ В) = 0 ∪ (A ∩ В) = A ∩ В.

Второй способ:

A ∩ В = (A ∪ В) ∩ В = В.

При втором способе доказательства использовался закон поглощения, который, вообще говоря, не входит в систему провозглашенных ранее аксиом, но справедливость которого, тем не менее, легко установить отдельно. Отсюда вывод: всякое доказательство зависит от тех средств, которыми мы располагаем.

Закон де Моргана можно доказать следующим образом. «Умножим» тождество слева и справа на скобку (а ∨ b), получим:

(a ∨ b) ∧ (а ∨ b) = (а ∧ b) ∧ (а ∨ b).

Так как а ∧ а = 0, то левая часть тождества равна нулю. Раскрывая скобки в правой части, убеждаемся, что и она равна нулю.

По аналогии с этим доказательством, вполне правдоподобным кажется и такое доказательство закона поглощения:

а = а ∧ (а ∨ b).

Обе части тождества «умножаем» на скобку (а ∨ b):

а ∧ (а ∨ b) = а ∧ (а ∨ b) ∧ (а ∨ b).

Используя закон идемпотентности, приходим к тождеству: 

а ∧ (а ∨ b) = а ∧ (а ∨ b).

Однако такое доказательство не совсем корректно. Здесь мы заранее знали, что закон поглощение — истинное тождество. Если же нам заранее не известно, справедливо тождество или нет, то использованный только что прием может привести к ошибке. Возможно лишь такое «умножение» и «сложение», которое отвечает законам нуля и единицы, т.е. а ∧ а = 0, а ∨ а = 1. Для иллюстрации сказанного возьмем заведомо ложное тождество: 

(а ∧ b) ∨ (а ∧ с) ∨ (а ∧ с) = (а ∧ b) ∨ (а ∧ с).

Воспользуемся законом поглощения в виде:

а = а ∨ (а ∧ с).

«Сложив» его с исходным выражением, получим тождество:

(а ∧ b) ∨ (а ∧ с) ∨ (а ∧ с) ∨ а =

= (а ∧ b) ∨ (а ∧ с) ∨ (а ∧ с) ∨ а,

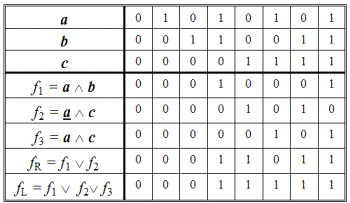
что должно доказывать справедливость исходного выражения. Однако с помощью таблиц истинности (табл. 1.18) легко установить, что это не так. Две нижние строки, соответствующие правой ( f_R ) и левой ( f_L ) частям исходного выражения, отличаются друг от друга. Это выглядит необычно, ведь прибавление к неравенству 1 < 3 одного и того же числа, например, (1 + 2) < (3 + 2) не обращает неравенство в тождество. И, тем не менее, исходное тождество было записано ошибочно. Истинным тождеством является:

(а ∧ b) ∨ (а ∧ с) ∨ (b ∧ с) = (а ∧ b) ∨ (а ∧ с).

Таблица 1.18

Закончим этот подраздел примерами решения задач.

1) Доказать тождество:

a → (b ∧ c) = a | (b | c).

Доказательство:

a → (b ∧ c) = a ∨ (b | c) = a | (b | c).

2) Доказать тождество:

a + (b ∧ c) = (a → b) ~ ((a + c) ∧ b).

Доказательство:

(a → b) ~ ((a + c) ∧ b) =

= (1 + a + ab) ~ (ab + bc) =

= 1 + (1 + a + ab) + (ab + bc) =

= a + (b ∧ c).

3) Доказать тождество:

(a ∧ b ∧ c) → (a ∨ b ∨ c) =

= (a → b) ∨ (b → c) ∨ (c → a).

Доказательство:

(a ∧ b ∧ c) ∨ (a ∨ b ∨ c) =

= (a ∨ b ∨ c) ∨ (a ∨ b ∨ c) =

= (a ∨ b) ∨ (b ∨ c) ∨ (c ∨ a) =

= (a → b) ∨ (b → c) ∨ (c → a).

4) Доказать тождество:

((a ↓ b) → (a + b)) ∧ ((a – b) → (a | b)) = a ∨ b.

Доказательство:

((a ↓ b) → (a + b)) ∧ ((a – b) → (a | b)) =

= ((a ∨ b) ∨ ((a ∧ b) ∨ (a ∧ b))) ∧ ((a ∨ b) ∨ (a ∨ b)) =

= ((a ∨ b) ∧ ((a ∨ b) ∨ (a ∨ b))) ∧ (a ∨ 1) =

= (x ∧ (x ∨ y)) ∧ 1 = x,

где x = a ∨ b, y = a ∨ b.

5) Доказать тождество:

(A ∪ C) ∩ (A ∪ B) ∩ (B ∪ C) ∩ (A ∪ B) ∩ (B ∪ C) = 0.

Доказательство:

A ∩ C ∩ (A ∪ C) = X ∩ X = 0,

где X = A ∩ C.

6) Доказать тождество:

(A ∪ B ∪ C) + (A ∩ B ∩ C) =

= (A ∪ B ∪ C) – (A ∩ B ∩ C).

Доказательство:

(A ∪ B ∪ C) + (A ∩ B ∩ C) =

= ((A ∩ B ∩ C) ∩ (A ∩ B ∩ C)) ∪

∪ ((A ∪ B ∪ C) ∩ (A ∪ B ∪ C)) =

= 0 ∪ ((A ∪ B ∪ C) ∩ (A ∪ B ∪ C)) =

= (A ∪ B ∪ C) – (A ∩ B ∩ C).

7) Доказать тождество:

((A ∪ B) ∩ (B ∪ C)) ∪ ((A ∪ C) ∩

∩ (B ∪ C) ∩ (A ∪ B)) = 1.

Доказательство:

((A ∪ B) ∩ (B ∪ C)) ∪ ((A ∪ C) ∩ (B ∪ C) ∩ (A ∪ B)) =

= (B ∪ (A ∩ C)) ∪ ((A ∪ C) ∩ (B ∪ (A ∩ C))) =

= (B ∪ X) ∪ (X ∩ (B ∪ X)) =

= (B ∪ X) ∪ (X ∩ B) =

= (B ∪ X) ∪ (B ∪ X) = 1,

где X = (A ∩ C).

8) Преобразовать в СДНФ функцию:

f = (x + z) – (x → y).

Решение:

f_СДНФ = (x + z) – (x → y) =

= (x ∨ z) ∧ (x ∨ z) ∧ x ∧ y =

= (x ∨ z) ∧ x ∧ y = x ∧ y ∧ z.

Правильность нахождения f_СДНФ проверим с помощью таблицы истинности (табл. 1.19).

Таблица 1.19

 

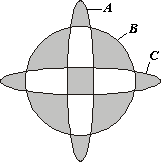
9) Используя операции над множествами, представить заштрихованные области рис. 1.18 в виде компактного аналитического выражения.

 

Рис. 1.18

Решение: заштрихованные области можно представить четырьмя конституентами:

(A ∩ B ∩ C) ∪ (A ∩ B ∩ C) ∪ 

∪  (A ∩ B ∩ C) ∪ (A ∩ B ∩ C) =

= (A ∩ ((B ∩ C) ∪ (B ∩ C))) ∪ 

∪  (A ∩ ((B ∩ C) ∪ (B ∩ C))) =

= (A ∩ (B ~ C)) ∪ (A ∩ (B + C)) =

= (A ∩ (B ~ C)) ∪ (A ∩ (B ~ C)) =

= A ~ B ~ C.