Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

1.5. Операции над предикатами и кванторами

Решетки вообще и булеан в частности

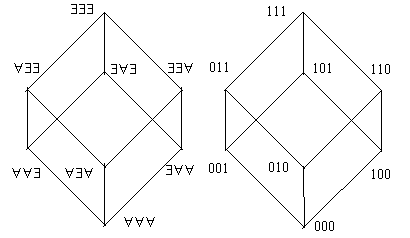
Процедура составления истинных клауз из предикатов с кванторами, описанная в предыдущем подразделе, позволяет построить булеан из кванторов (рис. 1.20 слева).

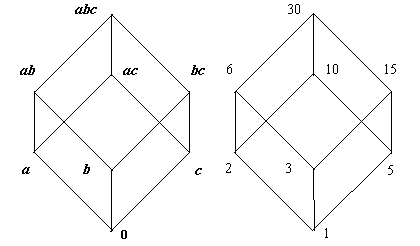
Булеан — распространенный математический объект. Так, если в кванторном булеане все символы ∀ заменить на 0, а ∃ — на 1, то получим булеан на 0,1-векторах (рис. 1.20 справа). Если дано множество из элементов a, b, c, то все его подмножества образуют точно такой же булеан (рис. 1.21 слева). Наконец, приведем пример из арифметики: делители числа 30 образуют аналогичный булеан (рис. 1.21 справа).

Булеан есть частично упорядоченное множество, на котором действуют законы логики множеств. Чтобы раскрыть его свойства, введем несколько определений.

Рис. 1.20

Рис. 1.21

Множество элементов любой природы называется линейно-упорядоченным, если любые два его элемента a и b связаны отношением порядка — либо a ⇒ b, либо b ⇒ a.

Множество называется частично упорядоченным, если имеются по крайней мере два несопоставимых элемента, на которые не распространяется отношение порядка. 

Верхней границей подмножества Q ⊂ R называют такой элемент r ∈ R, что для всех q ∈ Q справедливо отношение порядка q ⇒ r. Нижней границей подмножества Q ⊂ R называют такой элемент r' ∈ R, что для всех q ∈ Q справедливо отношение r' ⇒ q. Наименьшая верхняя граница называется супремумом (sup Q), а наибольшая нижняя граница — инфимумом (inf Q).

Помимо супремума и инфимума, вводятся понятия точной верхней грани и точной нижней грани, которые могут совпадать или не совпадать, соответственно, с супремумом и инфимумом. Точную верхнюю грань обозначим через дизъюнкцию a ∨ b, точную нижнюю грань — через конъюнкцию a ∧ b. Тогда в общем случае имеем:

a ∨ b ⇒ sup (a, b), inf (a, b) ⇒ a ∧ b.

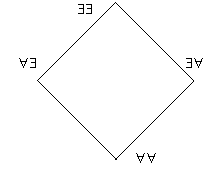
Множество R называется решеткой, если каждая пара его элементов обязательно имеет один супремум и один инфимум. Множество ∀∀, ∀∃, ∃∀ и ∃∃ (рис. 1.22) образует решетку, так как удовлетворяет указанному требованию, например:

sup (∀∃, ∃∃) = ∃∃, sup (∀∃, ∃∀) = ∃∃,
inf (∀∃, ∃∃) = ∀∃, inf (∀∃, ∃∀) = ∀∀.

Рис. 1.22

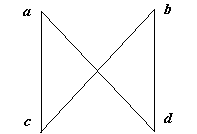
Множество a, b, c, d (рис. 1.23) не образует решетки, так как a и b имеют два инфимума и ни одного супремума, элементы c и d имеют два супремума и ни одного инфимума.

Рис. 1.23

Решетка называется булевой, или булеаном, если ее элементы удовлетворяют законам булевой логики — коммутативности, ассоциативности, дистрибутивности, нуля и единицы. Для кванторных решеток все четыре закона выполняются:

∀∀∃ ∨ ∀∃∀ = ∀∃∀ ∨ ∀∀∃,
(∀∃∀ ∨ ∃∀∀) ∨ ∃∃∀ = ∀∃∀ ∨ (∃∀∀ ∨ ∃∃∀),
(∀∀∃ ∧ ∃∀∀) ∨ ∀∃∀ = (∀∀∃ ∨ ∀∃∀) ∧ (∃∀∀ ∨ ∀∃∀),
∀∃∀ ∨ ∃∃∃ = ∃∃∃, ∀∃∀ ∧ ∃∃∃ = ∀∃∀,
∀∃∀ ∨ ∀∀∀ = ∀∃∀, ∀∃∀ ∧ ∀∀∀ = ∀∀∀.

Поскольку в кванторном булеане предполагаются только положительные предикаты, т.е. отсутствуют обратные элементы, типа ∀∃∀, то и в законе для нуля и единицы отсутствуют равенства, отражающие взаимное дополнение элементов. Однако вместо ∀∀∀ и ∃∃∃ можно взять полностью нулевой и единичный векторы, тогда уже все законы нуля и единицы будут выполняться, например:

∀∃∀Р ∨ ∃∀∃Р = 1, ∀∃∀Р ∧ ∃∀∃Р = 0.

Если для кванторов справедливы аксиомы логики множеств, то на них должны распространяться и все выводимые из них тождества, например, закон де Моргана:

∀∃∀ ∨ ∃∀∀ = ∀∃∀ ∧ ∃∀∀.

Аксиома порядка, которая может быть выражена клаузами:

∀∀∃, ∃∀∀ ⇒ ∀∀∃,     ∃∃∀ ⇒ ∀∀∃; ∃∃∀, ...

также имеет место в логике предикатов.

На первый взгляд выражения типа

∀∀∃ ⇒ ∀∀∃ ∧ ∃∀∃,    ∀∀∃ ∨ ∃∀∃ ⇒ ∃∀∃,

противоречат аксиоме порядка. Однако подобные клаузы всегда заменимы тождествами, поэтому их можно представить аксиомой порядка. Тождества возникают для линейно-упорядоченных элементов, каковыми и являются элементы ∀∀∃ и ∃∀∃:

sup (∀∀∃, ∃∀∃) = ∀∀∃ ∨ ∃∀∃ = ∃∀∃,
inf (∀∀∃, ∃∀∃) = ∀∀∃ ∧ ∃∀∃ = ∀∀∃.

Несопоставимые же элементы, к которым относятся, например, элементы ∀∃∃ и ∃∀∀, уже не будут описываться тождествами, а только отношением порядка:

∀∃∃ ∨ ∃∀∀ ⇒ sup (∀∃∃, ∃∀∀),
inf (∀∃∃, ∃∀∀) ⇒ ∀∃∃ ∧ ∃∀∀.

Так как

sup (∀∃∃, ∃∀∀) = ∃∃∃,     inf (∀∃∃, ∃∀∀) = ∀∀∀,

в логике предикатов будут возникать совершенно специфические клаузы, не сводящиеся к аксиоме порядка, типа —

∀∃∃ ∨ ∃∀∀ ⇒ ∃∃∃ , ∀∀∀ ⇒ ∀∃∃ ∧ ∃∀∀.

Рассматривая булеаны, нельзя не упомянуть о законе четырехполюсника. Действие его продемонстрируем сначала на числовом булеане делителей числа 30 (см. рис. 1.23). Если наибольший общий делитель (НОД) двух чисел a и b обозначить конъюнкцией (a ∧ b), а наименьшее общее кратное (НОК) — через дизъюнкцию (a ∨ b), то в отношении этих двух арифметических понятий будут действовать все четыре закона булевой логики.

Убедимся в справедливости закона дистрибутивности:

(a ∧ b) ∨ c = (a ∨ c) ∧ (b ∨ c);
при a = 6, b = 10 и c = 5, получим:
(6 ∧ 10) ∨ 5 = (6 ∨ 5) ∧ (10 ∨ 5),
или 2 ∨ 5 = 30 ∧ 10, или 10 = 10.

Но из арифметики известен закон: произведение любых двух чисел равно произведению их НОД и НОК: a · b = (a ∨ b) · (a ∧ b). В частности, 6 · 10 = (6 ∨ 10) · (6 ∧ 10) = 30 · 2. Этот арифметический закон является следствием булеановой структуры делителей чисел.

Подобный закон имеет место в любом булеане (хотя смысл операций в нем может существенно меняться) и называется он законом четырехполюсника. Четыре полюса, соответствующие числам 6, 10, 2 и 30, взятые на булеане подмножеств (рис. 1.22), связаны соотношением:

{a, b} ⊗ {a, c} = {{a, b} ∪ {a, c}} ⊗ {{a, b} ∩ {a, c}}.

Под символом ⊗ понимается прямое сложение множеств, при котором повторяющиеся элементы не удаляются, в частности:

{a, b, c} ⊗ {a} = {a, b, a, c}.

Закон четырехполюсника выполняется и для 0,1-векторов (рис. 1.21). Прямое сложение заменяется обычным сложением единиц:

(111) + (001) = ((011) ∨ (101)) + ((011) ∧ (101)); 3 + 1 = 4.

Число единиц в 0,1-векторе a будем называть его модулем или длиной и обозначать | a |. Из табл. 1.25 и табл. 1.26 выпишем в символической форме модули предикатных векторов:

|Р(a)| = |Р(b)| = 2, |∃| = 3, |∀| = 1;
|Р(k, m)| = 8, |∃∃| = 15, |∀∃| = 9, |∃∀| = 7, |∀∀| = 1.

Нетрудно убедиться в справедливости закона четырехполюсника для двухмерного предикатного булеана:

|∃∃| + |∀∀| = |∀∃ ∨ ∃∀| + |∀∃ ∧ ∃∀|; 15 + 1 = 11 + 5 = 16.

Таблица истинности для трехместных предикатов будет уже состоять из 256 строк. Чтобы определить модули 0,1-векторов кванторного булеана, таблицу истинности можно и не строить, но провести тщательный комбинаторный анализ. В итоге получим:

|∃∀∀| = 31, |∀∃∀| = 49, |∀∀∃| = 81, |∃∃∀| = 175, |∃∀∃| = 207, |∀∀∃| = 225, |∀∀∀| = 1, |∃∃∃| = 255, |Р(k, m, n)| = 128.

Кванторный булеан 3-го порядка наложен на векторный булеан 256-го порядка, причем его нижняя точка совпадает не с нулевым вектором, а с вектором первого уровня (00...01), верхняя же точка лежит на предпоследнем уровне (01...11). Таким образом, кванторный булеан оказывается немного развернутым относительно векторного булеана. Тем не менее, закон четырехполюсника для него тоже выполняется, в частности:

|∀∀∃| + |∀∃∀| = |∀∀∃ ∨ ∀∃∀| + |∀∀∃ ∧∀ ∃∀|;
81 + 49 = 105 + 25 = 130.

Вообще, величина модуля вектора a является важной собственной характеристикой клауз, например:

|∃∀∀| ⇒ |∀∃∀ ∨ ∃∃∀|, 31 ⇒ 151;
|∀∀∃ ∨ ∀∃∀| ⇒ |∀∃∃|, 105 ⇒ 225.

и тождеств, например: 57 = 57 для закона дистрибутивности:

|(∀∀∃ ∧ ∃∀∀) ∨ ∀∃∀| = |(∀∀∃ ∨ ∀∃∀) ∧ (∃∀∀ ∨ ∀∃∀)|.

С помощью модулей можно осуществлять частичную проверку правильности логических действий, хотя в случае многоместных предикатов для такого контроля понадобится уже компьютер, поскольку величина модулей даже для четырехместных предикатов исчисляется сотнями тысяч:

|∀∃∃∃| + |∃∀∃∃| = 65025 + 63135 = 128160.