Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
1.5. Операции над предикатами и кванторами
Построение доказательств в логике предикатов
Основной задачей логики предикатов является установление истинности предикатных тождеств и клауз. Обозначим через Pi какой-либо предикат с произвольным числом аргументов, а через qi соответствующую ему кванторную группу. Тогда, например, закон дистрибутивности примет вид:
q1 P1 ∨ (q2 P2 ∧ q3 P3) = (q1 P1 ∨ q2 P2) ∧ (q1 P1 ∨ q3 P3).В том, что он выполняется для одноместных предикатов, можно убедиться через процедуру конкретизации, к которой мы уже не раз прибегали:
x = a, b; q1 = ∀x, P1 = A(x);
y = c, d; q2 = ∃y, P2 = B(y);
z = e, f; q3 = ∀z, P3 = C(z).
[A(a) ∧ A(b)] ∨ ([B(c) ∨ B(d)] ∧ [C(e) ∧ C(f)]) =
= ([A(a) ∧ A(b)] ∨ [B(c) ∨ B(d)]) ∧
∧ ([A(a) ∧ A(b)] ∨ [C(e) ∧ C(f)]).От того, что в квадратных скобках появится вместо дизъюнкции конъюнкция, и наоборот, а также вместо одноместных предикатов будут фигурировать различные многоместные предикаты суть тождества не изменится. Оно останется истинным, в силу справедливости законов логики множеств и принципа суперпозиции, который гласит: замена какой-либо константы другой константой или даже группой констант не может повлиять на истинность тождества. Именно отсюда проистекает уверенность в справедливости законов логики множеств и по отношению к предикатам.
Те же рассуждения можно провести и в отношении логики высказываний. Она отличается от логики Буля аксиомой порядка —
q1 P1 , q2 P2 ⇒ q1 P1.Процедура конкретизации сводит предикатную аксиому порядка к простому высказыванию, так что если клауза верна для высказываний, она будет справедлива и для предикатов.
Как показывает практика, много ошибок приходится на неправильное обозначение предикатов при их, в принципе, правильной идентификации. Следует помнить, что положительный предикат должен иметь больше единиц, чем отрицательный. Будет допущена ошибка, если противоречие A1, A2 ⇒ 0 записать как A2, A1 ⇒ 0.
Перейдем к анализу конкретных предикатных выражений.
Пример 1. Пусть дано следующее тождество:
(∃x∀yP(x, y) ∨ ∃u∀vP(v, u)) ∧ (∀v∃uP(v, u) ∧
∧ ∃y∀xP(x, y)) = ∃x∀yP(y, x) ∧ ∀u∃vP(u, v).Здесь можно ввести следующие обозначения:
A = ∀x∃yP(x, y) = ∀v∃uP(v, u) = ∀u∃vP(u, v),
B = ∃u∀vP(v, u) = ∃y∀xP(x, y) = ∃x∀yP(y, x).В этих обозначениях тождество выглядит следующим образом:
(A ∨ B) ∧ (A ∧ B) = B ∧ A.Производя элементарные преобразования, мы можем убедиться в справедливости последнего равенства. Следовательно, и исходное тождество составлено верно.
Пример 2. Пусть дана предикатная клауза:
∀x∃yP(x, y) → ∀vP(a, v), ∀x P(a, x) →
→ ∃x∀yP(y, x) ⇒ ∀u∃vP(u, v) → ∃v∀uP (u, v).Введем обозначения:
A = ∀x∃yP(x, y) = ∀u∃vP(u, v),
B = ∀vP(a, v) = ∀xP(a, x),
C = ∃x∀yP(y, x) = ∃v∀uP(u, v).Получим:
A → B, B → C ⇒ A → C.Как известно, формула транзитивности верна, следовательно, и предикатная клауза тоже верна.
Итак, доказательство справедливости первых двух предикатных выражений свелось к простой процедуре идентификации их с соответствующими выражениями, существующими в логике Буля и логике высказываний. Рассмотрим более сложные примеры.
Пример 3. Доказать истинность клаузы:
∀v∃uP(u, v) → ∀u∀vP(u, v), ∃x∀yP(x, y)⇒∀uP(u, u).Введем обозначения:
A1 = ∃x∀yP(x, y), A2 = ∀v∃uP(u, v),
B1 = ∀u∀vP(u, v), B2 = ∀uP(u, u).В этих обозначениях клауза будет иметь вид:
A2 → B1, A1 ⇒ B2 или A2 ∨ B1, A1, B2 ⇒ 0.По методу резолюций данное противоречие возможно, если возможны два других противоречия —
A1, A2 ⇒ 0, B1, B2 ⇒ 0.Список из восемнадцати клауз, который мы вывели из табл. 1.26, предоставляет нам две истинных клаузы под номером 6 и 7. Если их представить в форме противоречия, то они будут полностью отвечать последним двум выражениям:
∃x∀yP(x, y), ∀y∃x P(x, y) ⇒ 0, ∀x∀yP(x, y), ∀x P(x, x) ⇒ 0.Таким образом, истинность исходной клаузы можно считать установленной.
Пример 4. Доказать истинность клаузы:
∀zB(z, z) → ∃x∃yB(x, y), ∃z∀yA(z, y) → ∀u∀vB(v, u),
∃x A(b, x) ⇒ ∃z∃xB(x, z) ∧ ∃z∀yA(z, y).Процедура идентификации приводит к следующим выкладкам:
A1 = ∀z∃yA(z, y), A2 = ∃xA (b, x),
B1 = ∀u∀vB(v, u) = ∀z∀xB(x, z),
B2 = ∀zB(z, z), B3 = ∀x∃yB(x, y);
B2 → B3, A1 → B1, A2 ⇒ B1 ∧ A1;
B2 ∨ B3, A1 ∨ B1, A2 ⇒ 0.
A1, A2 ⇒ 0, ∀x∃yA(x, y), ∃yA(k, y) ⇒ 0,
B1, B2 ⇒ 0, ∀x∀yB(x, y), ∀xB(x, x) ⇒ 0,
B1, B3 ⇒ 0, ∀x∀yB(x, y), ∀x∃yB(x, y) ⇒ 0.Отсюда следует истинность исходной клаузы.
Пример 5. Докажем справедливость клаузы:
∀x∃yA(x, y) ∨ ∃y∀xB(x, y) ∨ ∀u∀v∀wC(u, v, w), ∀y∃xA(y, x) →
→ ∀x∀y C(x, y, b), ∃x∀yB(y, x) → ∀u∀vC(u, v, a) ⇒
⇒ ∀x∃y∃zC(x,z, y) ∧ ∃u∀v∃wC (u, v, w).Доказательство:
A = ∀x∃yA(x, y) = ∀y∃xA(y, x), B = ∃y∀x B(x, y) = ∃x∀yB(y, x),
C' = ∀x∃y∃zC (x, z, y), C'' = ∃u∀v∃wC(u, v, w), C1 = ∀u∀vC(u, v, a),
C2 = ∀x∀yC(x, y, b), C3 = ∀u∀v∀wC(u, v, w).
A ∨ B ∨ C3, A ∨ C2, B ∨ C1 ⇒ C' ∧ C''.Воспользуемся свойством булеана:
C = ∀x∀y∃zC(x, y, z) = inf (C', C'') ⇒ C' ∧ C''.Тогда соответствующие противоречия для компенсации C1, C2 и C3 будут удовлетворены элементом C:
C1, C ⇒ 0 , C2, C ⇒ 0, C3, C ⇒ 0.После использования этого математического приема доказательство исходной клаузы становится очевидным.
Пример 6. Доказать истинность клаузы:
∀x∀yA(x, y, c) ∨ ∀y∃zA(a, y, z), ∃yA(a, y, c) ∨
∨ ∃zA(b, a, z), ∀x∀zA(x, a,z) ∨ ∀y∀zA(b, y, z) ⇒ ∀x∀zA(x, b, z).Доказательство:
A' = ∀x∀yA(x, y, c), B' = ∀x∀zA(x, a, z), A'' = ∀y∀zA(a, y, z),
B'' = ∀y∀zA(b, y, z), A = ∃yA(a, y, c) = inf (A', A''),
B = ∃zA(b, a, z) = sup (B', B''), C = ∀x∀zA(x, b, z);
A' ∨ A'', inf (A', A'') ∨ sup (B', B''), B' ∨ B'' ⇒ C.Инфимум, супремум, верхняя и нижняя грани здесь частично конкретизированы; элемент C не влияет на истинность исходной клаузы. Продолжить доказательство клаузы далее уже не составит большого труда.
Пример 7. Любая семантика логики высказываний может быть выражена в предикатной форме. В качестве примера возьмем легенду о кассире и водителе. Для нее введем следующие предикаты:
A(x) — x говорит правду,
B(x, y) — x находится внутри помещения y,
C(x, z) — x способен слышать звуки z.Область определения переменных:
x = {a, b}, где a — кассир, b — водитель;
y = {c, ...}, где c — комната отдыха;
z = {d, ...}, где d — звуки выстрелов.Содержание посылок и заключений следователя нами уже было раскрыто в разделе логики высказываний; здесь же приведем только их предикатную запись и необходимые разъяснения:
Р1 = А(a) → В(b, c), Р2 = В(b, c) → ∀zС(b, z),
Р3 = ∀zС(b, z) → С(b, d), Р4 = А(b) → C(b, d).В предикатной форме посылка Р3 является тавтологией, так как квантор существования можно расписать:
Р3 = ∃zС(b, z) ∨ С(b, d) = С(b, d) ∨ ... ∨ С(b, d) = 1.Тавтология не влияет на процедуру установления истинности клаузы и поэтому может быть удалена из перечня посылок, что мы и сделаем. Использование кванторов позволяет также несколько иначе интерпретировать заключение С1: «не все x говорят правду» или «существует x, который говорит ложь» —
С1 = А(a) → A(b) = А(a) ∨ A(b) = ∃xA(x) = ∀xA(x).Ложное второе следствие С2 тоже может быть записано через кванторы двумя эквивалентными способами: «все x говорят правду» или «нет ни одного x, который бы обманывал» —
С2 = А(a) ∧ A(b) = ∀xA(x) = ∃xA(x).Формальная запись всей легенды без Р3 и с заключением С1 будет:
А(a) → В(b, c), В(b, c) → ∀zС(b, z), А(b) → C(b, d) ⇒ ∃xA(x).Истинность ее установим методом резолюций:
А(a) ∨ В(b, c), В(b, c) ∨ ∀zС(b, z), А(b) ∨ C(b, d), ∀xA(x) ⇒ 0.Это противоречие имеет место, так как все клаузы, отвечающие необходимым склейкам, истинны:
В(b, c) ⇒ В(b, c), ∀zС(b, z) ⇒ C(b, d),
∀xA(x) ⇒ А(a), ∀xA(x) ⇒ А(b).Пример 8. Дана следующая простая легенда:
Если Иван повсюду ходит за Петром, а Петр находится в институте, то где же будет находиться Иван?P(x, y) — « x находится там, где y »
Составим клаузу:
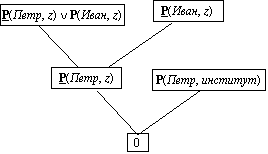
∀z(P(Петр, z) → P(Иван, z)), P(Петр, институт) ⇒ ∃z(P(Иван, z).По существу, здесь доказывается следующее предложение: существует ли такое место z, где находился бы Иван. Преобразуем исходную клаузу в противоречие:
P(Петр, z) ∨ P(Иван, z), P(Петр, институт), P(Иван, z) ⇒ 0.Здесь и ниже кванторы общности мы будем опускать, поскольку кванторы существования отсутствуют. Доказательство клаузы оформим в виде дерева (рис. 1.24)
Рис. 1.24
При конкретизации z = институт, доказывается, что действительно существует такое место z, в котором мог бы находиться Иван.
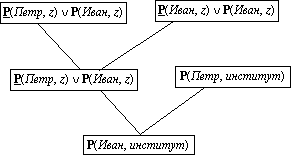
Однако метод резолюций можно модифицировать так, чтобы итогом доказательства был не ноль, а непосредственно ответ в предикатной форме: Иван находится в институте. Этого можно достичь, если к тому, что требуется доказать, прибавить через дизъюнкцию противоположное утверждение, образовав таким образом тавтологию: P(Иван, z) ∨ P(Иван, z). Тогда дерево логического вывода будет выглядеть так, как это показано на рис. 1.25.
Рис. 1.25
Большинство задач с использованием предикатов носит поисковый характер. Поисковые задачи реализуются средствами языка логического программирования ПРОЛОГ. Остановимся на основных структурных и функциональных элементах этого языка.
Поскольку логика высказываний имеет дело с любыми правильно построенными предложениями, существует серьезная опасность смешения объектных и субъектных предложений, а также предложений, взятых с различных иерархических уровней предметной области логики высказываний. Чтобы избежать указанной опасности, доказываемую задачу оформляют в виде отчетливой структуры древовидной формы. В качестве корня дерева выбирается некая цель С, истинность которой необходимо установить. Она всегда фигурирует в качестве заголовка правила, которое представляет собой хорновскую клаузу. Эти клаузы в данном случае удобно записать в обратном порядке: С ⇐ В1, В2, ... Каждая из посылок Вi представляет собой подцель основной цели С и зависит, в свою очередь, от других правил Aij:
В1 ⇐ А11, А12, ... , В2 ⇐ А21, А22, ...Впрочем, в роли посылок Вi могут выступать не клаузы, а элементарные высказывания — факты. Далее посылки Aij опять могут быть либо заголовками новых правил, либо фактами. Так образуется иерархическая структура древовидной формы. В логических деревьях уже не возникает описанных выше парадоксов.
В ПРОЛОГе реализована процедура унификации, с помощью которой производится сравнение цели с правилами, а правила сопоставляются с фактами. В результате унификации переменным присваиваются конкретные значения, так что предикат цели становится истинным фактом в случае положительного исхода. Чтобы понять, как осуществляется унификация, разберем конкретный пример программы.
Пример 9. Имеется следующая легенда:
Ивана интересуют компьютеры, книги и автомобили. Петра интересует нечто, что интересует Ивана, но если это нечто является техникой и если это произведено в России. Известно, что компьютеры и автомобили — это техника. Кроме того, известно, что компьютеры производятся в Америке, а автомобили — в Америке и России. Вопрос: "Что интересует Петра?"Для удобства пользования программой все предикаты и конкретные значения переменных не кодируются отдельными буквами, а приводятся в словах непосредственно, передающих их семантику. Мы, однако, слева от текста программы приведем символьные выражения, чтобы далее у нас была возможность продемонстрировать в аналитической форме метод резолюций, который лежит в основе функционирования ПРОЛОГа. Будем помнить также, что все склейки осуществляются с квантором общности, хотя сам квантор не указывается.
Программа:
1) интерес (Иван, компьютеры). A(i, a)
2) интерес (Иван, книги). A(i, b)
3) интерес (Иван, автомобили). A(i, c)
4) интерес (Петр, x) A(p, x)
5) ⇐ интерес (Иван, x), A(i, x)
6) техника (x), T(x)
7) произведено(x, Россия). P(x, r)
8) техника (компьютеры). T(a)
9) техника(автомобили). T(c)
10) произведено (компьютеры, Америка). P(a, s)
11) произведено (автомобили, Америка). P(c, s)
12) произведено (автомобили, Россия). P(c, r)
Цель:
13) интерес (Петр, x). A(p, x)
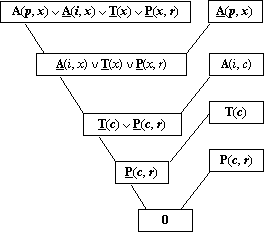
Данная программа позволяет составить следующее противоречие, которое может быть разрешено в рамках метода резолюций:
A(i, a), A(i, b), A(i, c), T(a), T(c), A(p, x) ∨ A(i, x) ∨
∨ T(x) ∨ P(x, r), P(a, s), P(c, s), P(c, r), A(p, x) ⇒ 0.Ноль можно получить только в том случае, если x = c.
Тогда A(p, c) ∨ A(i, c) ∨ T(c) ∨ P(c, r) нейтрализуется предикатами под номерами 3, 9, 12 и 13. Поиск нужного значения x как раз и осуществляется через процедуру унификации, которую можно отследить путем трассировки программы. Трассировка — это пошаговое протоколирование процесса выполнения программы.Трассировка программы:
1. В: цель ( ) - 13,
2. В: интерес (Петр, _ ) - 1,
3. П: интерес (Петр, _ ) - 2,
4. П: интерес (Петр, _ ) - 3,
5. У: интерес (Петр, _ ) - 4,
6. В: интерес (Иван, _ ) - 5,
7. У: интерес (Иван, компьютеры) - 1 у,
8. В: техника (компьютеры) - 6,
9. У: техника (компьютеры) - 8,
10. В: произведено (компьютеры, Россия) - 7,
11. П: произведено (компьютеры, Россия) - 10,
12. П: произведено (компьютеры, Россия) - 11,
13. Н: произведено (компьютеры, Россия) - 12,
14. П: интерес (Иван, _ ) - 5,
15. У: интерес (Иван, книги) - 2 у,
16. В: техника (книги) - 6,
17. П: техника (книги) - 8,
18. Н: техника (книги) - 9,
19. П: интерес (Иван, _ ) - 5,
20. У: интерес (Иван, автомобили) - 3,
21. В: техника (автомобили) - 6,
22. П: техника (автомобили) - 8,
23. У: техника (автомобили) - 9,
24. В: произведено (автомобили, Россия) - 7,
25. П: произведено (автомобили, Россия) - 10,
26. П: произведено (автомобили, Россия) - 11,
27. У: произведено (автомобили, Россия) - 12,
28. У: цель ( ) - 13.Здесь использованы следующие обозначения: В — вызов нового предиката; П — повторный вызов предиката; У — успешное завершение процедуры унификации, т.е. вызванный предикат отвечает какому-либо факту; Н — неуспешное завершение унификации; у — указатель, который говорит о том, что существует по крайней мере еще один факт с подходящей унификацией. Символ подчеркивания на месте x называется анонимной переменной и полностью заменяет x при трассировке программы. Строка трассировки заканчивается числом, отвечающим номеру листинга программы.
Для того чтобы ответить на вопрос «Что интересует Петра?» или в предикатной форме — интерес (Петр, x), ПРОЛОГ-система ищет факты и заголовки правил, сопоставимые с целью. Поиск всегда начинается с первой строки программы. Первые три факта несопоставимы с целью; далее следует правило, заголовок которого заменяется на три подцели. В строке 6 вызывается первая подцель. Затем ПРОЛОГ-система возвращается в начало программы, где ее ожидает «успех». Выставляется указатель «у», к которому система вернется в случае «неуспеха» (он может появиться в другом месте программы). В строке 8 производится вызов второй подцели — техника (компьютеры), для которой тут же находится подходящий факт (строка 9). Однако для третьей подцели – произведено (компьютеры, Россия) — нужного факта не находится (строка 13). Тогда переменная x освобождается от своей прежней конкретизации (компьютеры) и принимает новое значение — книги. Эта конкретизации не удовлетворяет вторую подцель (строка 18). Переменная вновь освобождается и принимает значение автомобили. При этой конкретизации удовлетворены все три подцели, следовательно, и поиск ответа на основной вопрос заканчивается «успехом»: Петра интересуют автомобили, т.е. интерес (Петр, автомобили) является тем конкретизированным предикатом, при котором обеспечена истинность всей клаузы.
Рис. 1.26
Граф поиска ответа, сформулированного в виде цели интерес (Петр, x), представлен рис. 1. 26. Бинарное дерево получилось в итоге подстановок предметных констант на место переменных, правила заменялись фактами, а цель — подцелями. Трассировка показывает, что ПРОЛОГ-система не сразу вышла на это дерево склеек. В пунктах 7, 9 и 15 протокола трассирования также производились склейки, но они привели к «неуспеху». Скорейшее достижение цели зависит от правильного выбора стратегии поиска и искусства программирования.