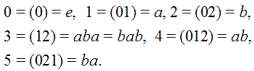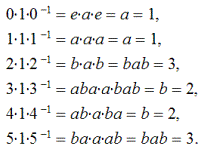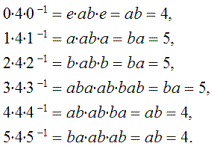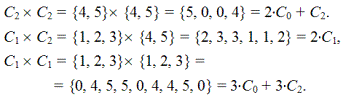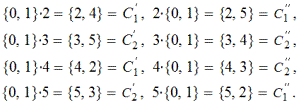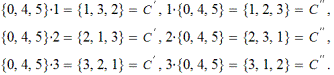
Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.2. Группы на матрицах и подстановках

Отношение эквивалентности

Изоморфизм — одна из основных форм эквивалентности. Две группы A и B считаются изоморфными, если можно найти такую трансформационную подстановку t, не принадлежащую ни A, ни B, что все элемента a трансформируются в элементы b:

b = t^–1 · a · t         (2.27)

В этом случае группы A и B имеют одинаковые таблицы умножения. Однако идентичность таблиц является не всегда очевидным фактом.

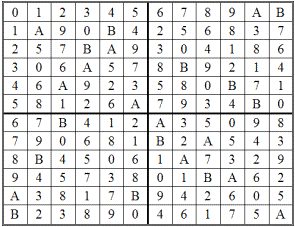
Таблица 2.29

Пусть дана конкретная таблица умножения — табл. 2.29. Поскольку она не симметрична относительно главной диагонали и имеет на ней два тождественных элемента, можно предположить, что группа, которую представляет табл. 2.29, по-видимому, является группой . Следовательно, нужно установить идентичность табл. 2.29 и 2.26. С этой целью из табл. 2.29 выберем, причем достаточно произвольно, регулярную подстановку 

4 = (042A78)(1B9356). 

Этой подстановке поставим в соответствие упорядоченную подстановку 

1 = (012345) (6789AB) 

эквивалентной циклической структуры, взятой из табл. 2.26.

Теперь воспользуемся следующим приемом. Считаем подстановку 1 верхней строкой трансформационной подстановки t, а подстановку 4 ее нижней строкой:

= (0)(147B6)(2)(3A589).

Далее запишем обратное к (2.27) преобразование подобия —

a = t · b · t^–1.

Подставим вместо b регулярные подстановки из табл. 2.29:

Строя по вновь полученным подстановкам a таблицу умножения, убеждаемся, что она совпадает с табл. 2.26. Следовательно, табл. 2.29 есть не что иное, как таблица умножения группы .

Изоморфизм является важной, но не единственной формой эквивалентности. Целью, даже поверхностного, морфологического анализа группы служит установление отношения эквивалентности между отдельными ее элементами. Всякое отношение эквивалентности, как мы уже знаем, разбивает группу на классы эквивалентных элементов. По причине коммутативности тождественного элемента e со всеми другими элементами группы, он всегда образует свой собственный класс. В группе может находиться несколько таких элементов, которые, как и тождественный элемент, коммутируют со всеми элементами группы. Тогда каждый из них будет образовывать свой класс эквивалентности. Совокупность таких элементов называется центром группы. Центр группы G, который обозначим через Z, всегда образует подгруппу в группе G. В коммутативных группах получается, что все элементы центральны.

Подгруппы G_i группы G делятся на собственные и несобственные. К несобственным относятся подгруппа тождественного элемента G₀ и сама группа G, все остальные подгруппы — собственные. Индексом подгруппы G_i в группе G, что обозначается как |G : G_i|, называется частное от деления порядка группы G (обозначается |G|) на порядок подгруппы |G_i|. В этом случае выполняются элементарные числовые соотношения:

|G : G_i| = |G| / |G_i|, |G_i| = |G| / |G : G_i|, |G| = |G : G_i| · |G_i|,

(путаницы между терминами индекс подгруппы и индекс подстановки обычно не возникает). Индекс всегда является целым числом. Это значит, что порядок подгруппы должен быть одним из делителей порядка группы. Поэтому, в частности, в группе шестого порядка не может быть подгрупп четвертого или пятого порядков. Но из факта существования того или иного делителя еще не следует, что обязательно должна существовать соответствующая ему подгруппа. Например, в группе тетраэдра T нет подгрупп шестого порядка.

Вообще говоря, подгруппы являются объектами морфологического анализа, с точки зрения отношения порядка, которым мы сейчас подробно заниматься не будем. Вместе с тем отметим, что эквивалентность элементов тесно связана с их иерархией, поэтому нередко оба вида отношений трудно рассматривать раздельно. Наш анализ, с точки зрения эквивалентности, начнем с первой некоммутативной группы диэдра, которую мы запишем как D₃:

Элемент 1 трансформируется по элементам D₃ следующим образом:

Отсюда видно, что элемент 1 сопряжен с элементами 2 и 3, т.е. в группе D₃ имеется класс эквивалентности —

C₁ = {1, 2, 3} = {a, b, bab} = {(01), (02), (12)},

(обозначение классов эквивалентности и коммутативных групп совпадают, но путаницы не возникает, так как классы рассматриваются только в некоммутативных группах). Если любой из этих элементов подвергнуть трансформации, он не даст в результате элементы 4 и 5, поскольку последние объединены в свой класс эквивалентности —

Таким образом, появился класс

C₂ = {4, 5} = {ab, ba} = {(012), (021)}.

Кроме того, имеется класс

C₀ = {0} = {e} = {(0)}.

Итак, группа диэдра D₃ разбивается на три класса эквивалентности — C₀, C₁, C₂, что согласуется с нашими комбинаторными рассуждениями.

Классы эквивалентности можно перемножать. Произведение классов C_i  · C_j есть множество произведений элементов, взятых из C_i и C_j, причем совпадающие элементы не опускаются. В результате перемножения целых классов всегда получаются тоже целое число классов:

В группе D₃ содержатся следующие несобственные подгруппы

G₀ = {0},   G = {0, 1, 2, 3, 4, 5}.

Три транспозиции образуют три собственных подгруппы второго порядка

G₁ = {0, 1},   G₂ = {0, 2},   G₃ = {0, 3}.

Еще одна собственная подгруппа образована 3-циклом —

G₄ = {0, 4, 5}.

Индексы подгрупп G₁, G₂, G₃ равны 3, а для G₄ — 2. Центр группы D₃ состоит из одного тождественного элемента —

Z = G₀ = {0}.

Подгруппы G₁, G₂, G₃ отличаются от G₄ не только порядком, но и еще одним важным обстоятельством: G₄ состоит из полных классов C₀ и C₂, в то время как эквивалентные элементы класса C₁ оказываются поделенными между различными подгруппами второго порядка. Это отличие между подгруппами выявляется при составлении так называемых классов смежности. Существуют левые и правые смежные классы, поскольку каждый элемент g из группы G, но не входящий в подгруппу G_i, может образовывать всевозможные произведения справа G_i g и слева gG_i. Найдем правые и левые смежные классы, например, для подгруппы G₁:

Левые и правые смежные классы для этой подгруппы не совпадают. Такая же картина наблюдается и для двух других подгрупп второго порядка. В отношении G₄ ситуация изменится:

Итак, для подгруппы G₄ левые и правые классы совпали: 

C ' = C". 

Такое положение вещей распространяется на любые подгруппы G_i, в состав которых входят полные классы сопряженности. Для них выполняются равенства:

G_i g = g G_i, G_i = g G_i g^–1.

Последнее выражение демонстрирует тесную связь между классами смежности и классами сопряженности. Поскольку для подгруппы G_i отдельно левые и отдельно правые классы смежности не пересекаются, они также являются классами эквивалентности, и так как подгруппа G_i не изменяется под трансформационным действием элемента g, ее называют инвариантной или нормальным делителем группы G (N = G_i ).