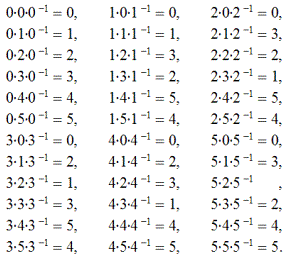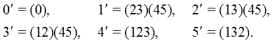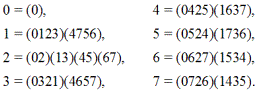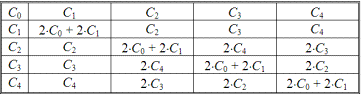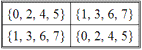Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.2. Группы на матрицах и подстановках

Факторгруппа, инвариант и внутренний автоморфизм

Введем понятие факторгруппы. С этой целью рассмотрим два класса смежности Nx и Ny (для нормального делителя N не имеет значения, какие классы — левые или правые). Выберем из этих классов по конкретному представителю: a ∈ Nx, b ∈ Ny и составим из них произведение a · b. Полученный таким образом новый элемент будет принадлежать классу смежности Nxy, что нетрудно доказать. Для этого запишем:

a · b = mx · ny = mx · n · e · y = mx · n · (x^–1x) · y =

= m · (xnx^–1) · xy = mlxy ∈ Nxy;

a = mx, b = ny; N = xN x^–1; m, n, l, lm ∈ N.

Представленное доказательство одновременно демонстрирует условие замкнутости, при котором один смежный класс Nx умножается на другой Ny и получается третий Nxy, причем все элементы-классы принадлежат группе G. Так при помощи нормального делителя N получилась факторгруппа, которую обозначают G / N. Роль тождественного элемента для факторгруппы G / N играет сам нормальный делитель N. В качестве обратных элементов для Nx и Ny выступают Nx^–1 и Ny^–1. Закон ассоциативности здесь также не нарушается. Порядок факторгруппы | G / N | равен индексу инвариантной подгруппы | G : N |.

В нашем примере с D₃ имеется только один нормальный делитель — подгруппа G₄, поэтому здесь можно построить только одну факторгруппу D₃ / G₄ с таблицей умножения — табл. 2.30.

Таблица 2.30

Из таблицы видно, как элементы группы D₃ проецируются на группу второго порядка. Такое отношение между группами называется гомоморфизмом. В случае построения именно факторгруппы получается так называемый естественный, или канонический, гомоморфизм. Но элементы группы D₃ можно проецировать ( → ) на любую подгруппу второго порядка, в том числе и на подгруппу, например G₁ = {0, 1}, т.е. имеет место изоморфизм:

D₃ / G₄ ≈ G₁: если D₃ → G₁,

то {0, 4, 5} → 0 и {1, 2, 3} → 1.

В этом специальном случае, когда элементы группы G проецируются на элементы своей подгруппы, гомоморфизм уже называется эндоморфизмом.

Добавим также, что нормальный делитель, по которому строится факторгруппа, называется ядром гомоморфизма. При эндоморфизме ядро проецируется на тождественный элемент неинвариантной подгруппы. В проекции D₃ → G₁ группа G₁ называется образом, а группа D₃ — прообразом.

Введем понятие внутреннего автоморфизма группы G, которое определяется следующим преобразованием:

x = g y g^–1.

Автоморфное преобразование отличается от похожего на него трансформационного тем, что элемент g фиксирован, а x и y пробегают все элементы группы G.

Найдем внутренний автоморфизм для нашей группы D₃:

Числа, отвечающее y, образуют верхнюю строку подстановок автоморфизма, а числа, отвечающие x, — нижнюю строку этих подстановок. Тогда в циклической форме подстановки внутреннего автоморфизма примут вид:

Вновь полученные подстановки образуют группу, изоморфную исходной группе D₃. Такое совпадение неслучайно и объясняется оно тем, что внутренний автоморфизм группы G всегда изоморфен факторгруппе G/Z. Так как центр Z группы D₃ состоит из единственного тождественного элемента, то и получилось:

D₃ / Z ≈ D₃ ≈ {0', 1', 2', 3', 4', 5' }.

Здесь надо помнить, что центр любой группы является ее нормальным делителем и построение по нему соответствующей факторгруппы всегда возможно.

Проведем морфологический анализ кватерниона :

Группа разбивается на пять классов сопряженности:

C₀ = {0}, C₁ = {2}, C₂ = {1, 3}, C₃ = {4, 5}, C₄ = {6, 7}.

Таблица умножения классов представлена табл. 2.31.

Таблица 2.31

Все подгруппы кватерниона G_i инвариантны. В группе имеется четыре нетривиальные подгруппы:

G₁ = {0, 2}, G₂ = {0, 1, 2, 3}, G₃ = {0, 2, 4, 5}, G₄ ={0, 2, 6, 7}.

Таблица умножения смежных классов для факторгрупп /G₃ и /G₁ представлены, соответственно, табл. 2.32 и табл. 2.33. Таблицы умножения для /G₂ и /G₄ аналогичны табл. 2.32.

Таблица 2.32

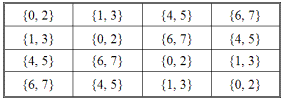
Таблица 2.33

Центр кватерниона состоит из двух элементов — Z = G₁ = {0, 2}. Следовательно, его внутренний автоморфизм будет состоять только из четырех подстановок (табл. 2.33):

/Z = {(0), (45)(67), (13)(67), (13)(45)} ≈ ,

внутренний автоморфизм кватерниона изоморфен группе .