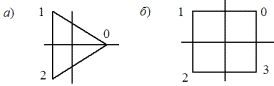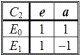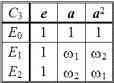Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.2. Группы на матрицах и подстановках

Геометрическая интерпретация групповых преобразований

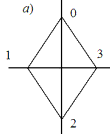
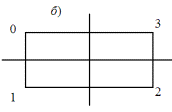
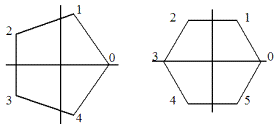
На рис. 2.3 изображены ромб и на рис. 2.4 прямоугольник. Вершины этих простых геометрических фигур образуют субстанционные, или базисные, множества, которые насчитывают по четыре элемента. Начав вращать эти симметричные фигуры относительно обозначенных на рисунке горизонтальных и вертикальных осей, а также вокруг необозначенных осей, направленных перпендикулярно к плоскости рисунка, мы получим множество отображений или операционных элементов в виде подстановок.

Рис. 2.3

Рис. 2.4

Таким образом, появляются две изоморфных группы подстановок типа для ромба —

e = (0),     a = (02),     b = (13),     ab = (02)(13);

для прямоугольника —

e = (0),   a = (01)(23),   b = (03)(12),   ab = (02)(13).

Здесь в обоих случаях число субстанционных элементов, представленных вершинами фигур, совпадает с числом операционных. Теперь изменим субстанционные множества: пусть для ромба в качестве базисных выступают два элемента — верхняя и нижняя его поверхности, а для прямоугольника — две его диагонали — 0-2 и 1-3. Тогда группы операционных элементов тоже уменьшатся в 2 раза и станут типа C₂.

Повороты геометрических фигур в пространстве представляют собой линейные преобразования (2.1), в которых в качестве операторов A могут выступать 0,1-матрицы. Степень периодичности матриц равна двум, значит их собственными значениями (2.11) являются числа (+1) и (–1). Положительная и отрицательная единицы образуют группу C₂, гомоморфную группе . В коммутативных группах каждый элемент образует класс эквивалентности. Поставим в соответствие каждому элементу группы столбец из собственных значений (табл. 2.36). Классы эквивалентности не пересекаются. Этот факт отражается в том, что скалярные произведения столбцов должны быть равны нулю. Следовательно, в табл. 2.36 все положительные и отрицательные единицы надо расставить так, чтобы произведение векторов-столбцов отвечало этим требованиям. Такая расстановка собственных значений автоматически приводит к выполнению условия ортонормированности и в отношении строк E_i, которые называются представлениями группы . Все представления у нас получились гомоморфными, причем представление E₀ является единичным, так как элементы группы проецируются на тривиальную группу тождественного элемента G₀ (или C₁). Проецирование → C₂ можно осуществить тремя способами — E₁, E₂ и E₃.

В группе C₄ так же, как и в группе , четыре элемента. С точки зрения геометрии, она отвечает вращению квадрата в плоскости рисунка (рис. 2.5б). Собственными значениями 0,1-матриц, которые соответствуют группе подстановок C₄:

e = (0),   a = (0123),   a² = (02)(13),   a³ = (0321),

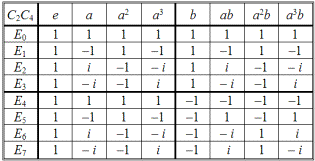
служат корни четвертой степени из единицы (см. табл. 2.37). Проецирование элементов группы C₄ на эти корни дает четыре возможных представления, два из которых (E₀ и E₁) являются гомоморфизмами, а два (E₂ и E₃) — изоморфизмами.

Рис. 2.5

Представление E₀ соответствует проецированию всей группы C₄ на единицу {e}; представление E₁ есть проекция C₄ на подгруппу {e, a²}; представления E₂ и E₃ осуществляют проецирование элементов C₄ на собственные значения 0,1-матриц, отвечающие элементам a и a³. Произведение столбцов a на a³ и строк E₂ на E₃ уже не равно нулю, т.е. изоморфные представления не будут ортогональными. Это связано с тем, что элементы a и a³ попадают в один абсолютный класс эквивалентности, в результате чего выполняются следующие соотношения:

E₀ · E₁ = E₀ · E₂ = E₀ · E₃ = E₁ · E₂ = E₁ · E₃ = 0, но E₂ · E₃ = 4.

Введенные понятия об относительном и абсолютном подобии позволяют объяснить наличие или отсутствие ортогональности между отдельными представлениями коммутативных групп.

Таблица представлений для группы C₂ тривиальна (табл. 2.38). Мы бы ее не приводили, если бы не одно обстоятельство: она поможет нам понять принцип построения таблиц представлений больших размерностей.

Таблица 2.36

Таблица 2.37

Таблица 2.38

Остановимся на вращениях в плоскости рисунка правильного треугольника (рис. 2.5а), пятиугольника (рис. 2.6а) и семиугольника, которые образуют простые циклические группы C₃, C₅ и C₇. Для них все представления являются изоморфизмами, за исключением единичного E₀: C₃ (табл. 2.39), C₅ (табл. 2.40), C₇ (табл. 2.41), причем прямая и обратная подстановки попадают в один абсолютный класс эквивалентности. Следовательно, в один класс неортогональных друг к другу представлений в группе C₅, например, попадут представления E₁ и E₄ или E₂ и E₃.

Таблица 2.39

Таблица 2.40

Таблица 2.41

Корни 3-й, 5-й и 7-й степени из единицы (ω_i) расставляются по строкам и столбцам таблиц представлений соответственно своим подстановкам. Это значит, что индексы при ω_i, например, для группы правильного пятиугольника C₅, чередуются в соответствии с индексами следующих четырех подстановок:

a = (01234),   a² = (02413),   a³ = (03142),   a⁴ = (04321).

Рис. 2.6

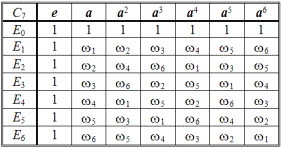
Согласно симметрии правильного шестиугольника (рис. 2.6б), группа C₆ имеет, помимо единичного класса {E₀}, еще два абсолютных класса гомоморфных представлений — {E₁}, {E₂, E₃}, а также один класс изоморфных представлений — {E₄, E₅}, которые расписаны в табл. 2.42. В ней приняты следующие обозначения корней: 

ω = ω⁴,     –ω² = ω⁵,     –1 = ω³.

Таблица 2.42

Обозначения для элементов представлений группы C₈ можно выбрать такие же, как и для группы C₆ (табл. 2.42), если помнить, что

1 = ω₀,     –1 = ω₄,     i = ω₂,     –i = ω₆,     –ω₃ = ω₇,     –ω = ω₅.

Однако при составлении табл. 2.43 использовалась методика чередования индексов корней при ω_i, согласно подстановкам группы C₈. Здесь изоморфный класс состоит уже не из двух, а из четырех представлений — {E₁, E₃, E₅, E₇}. Остальные классы абсолютной эквивалентности гомоморфны — {E₀}, {E₄}, {E₂, E₆}.

Таблица 2.43

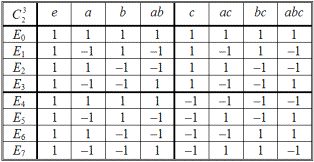
Две следующие таблицы представлений для коммутативных групп 8-ого порядка — = C₂ (табл. 2.44) и C₂C₄ (табл. 2.45) – получены из элементов (табл. 2.36) и C₄ (табл. 2.37), путем умножения их на 1 или –1, отвечающих группе C₂ (табл. 2.38).

Таблица 2.44

Таблица 2.45

Таблицы представлений для коммутативных групп больших порядков составляются по аналогии с рассмотренными. Далее переходим к анализу некоммутативных групп.

Начнем с группы диэдра D₃. Она отвечает вращению равностороннего треугольника (рис. 2.5а) не только в плоскости рисунка, но и в пространстве оси z, перпендикулярной к осям x и y. В группу D₃ входят шесть подстановок:

e = (0),     a = (012),     a² = (021),

b = (02),     ab = (01),     ba = (12),

которые разбиваются, как мы уже знаем, на три класса эквивалентности (для некоммутативных групп есть смысл говорить только об относительных классах эквивалентности):

C₀ = {e}, C₁ = {a, a²}, C₂ = {b, ab, ba}.

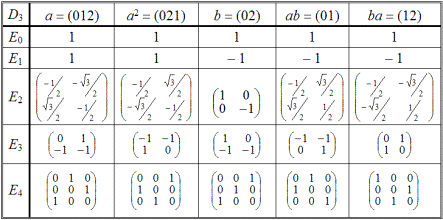
Этим классам отвечают два гомоморфных (E₀ и E₁) и одно изоморфное ортогональное представления — E₂ (табл. 2.46). Поскольку свойство некоммутативности уже не может быть воспроизведено с помощью одномерных представлений из собственных значений, E₂ является двухмерным. 

Таблица 2.46

Кроме того, в табл. 2.46 включено еще одно неортогональное, эквивалентное (относительно E₂) двухмерное представление E₃ и одно трехмерное E₄. Матрицы последнего представления отвечают приведенным подстановкам группы D₃ (в табл. 2.46 отсутствуют единичные матрицы).