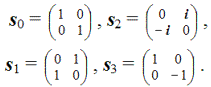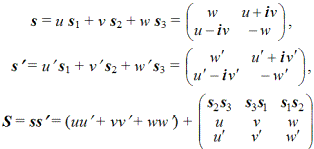Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.2. Группы на матрицах и подстановках

Октава и алгебра Клиффорда

Введем удвоение кватерниона, в результате чего получим октаву:

o = q₁ + Eq₂ = (a + ib + jc + kd) + E(A + iB + jC + kD) =

= a + ib + jc + kd + EA + IB + JC + KD.

Закон умножения базисных единиц октавы будет задаваться табл. 2.50. Она определяет закон умножения только для положительных базисных единиц (закон умножения для отрицательных единиц не сложно восстановить самим). Для октав перестает выполняться закон ассоциативности, так как:

(i j)E = K,     но    i(jE) = –K,

поэтому базисные единицы октавы уже не образуют группы.

Таблица 2.50

В квантовой физике часто приходится иметь дело с матрицами Паули, которые в математике называются спинорами:

Существует простая связь между спинорами и матрицами базисных единиц кватерниона:

i = is₂ = s₁s₃,     j = is₃ = s₂s₁,     k = is₁ = s₃s₂.

Закон ассоциативности для матриц Паули выполняется в силу общей природы матриц:

s₁(s₂s₃) = (s₁s₂)s₃ = –i.

Однако группы эти базисные единицы тоже не образуют, поскольку нарушен закон замкнутости. Тем не менее, на них можно построить любопытный математический объект — алгебру Клиффорда.

Алгебра Клиффорда на матрицах Паули представляет собой числовой агрегат следующего вида:

A = a₀s₀ + a₁s₁ + a₂s₂ + a₃s₃ + a₁₂s₁s₂ + a₂₃s₂s₃ + a₃₁s₃s₁ + a₁₂₃s₁s₂s₃.

В состав агрегата A входит один скаляр, три вектора, три бивектора и один тривектор (или псевдоскаляр). При перемножении таких агрегатов, в силу условий для спиноров s_is_j + s_js_i = 0 и s_i² = 1, будут возникать два типа умножения базисных единиц — внутреннее и внешнее. Внутреннее произведение (его еще называют скалярным) возникает тогда, когда s_i входит в базисную единицу n-вектора s₁s₂ ... s_n, например:

s₂ · s₁s₂s₃ = s₂s₁s₂s₃ = –s₁s₂s₂s₃ = –s₁s₃,

в результате чего, если говорить об общем случае, n-вектор переходит в (n – 1)-вектор. Внешнее произведение, или векторное, возникает тогда, когда s_i не входит в сложную базисную единицу s₁s₂ ... s_n, например:

s₂ ´ s₁s₃ = s₂s₁s₃ = –s₁s₂s₃, 

и тогда n-вектор переходит в (n + 1)-вектор. Поскольку путаницы между этими произведений не возникает, их можно не различать специальными символами « · » и « ´ », как это часто делают в векторной алгебре. Так, при перемножении двух векторов возникает скаляр и бивектор —