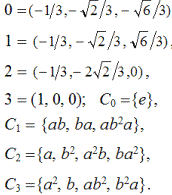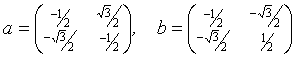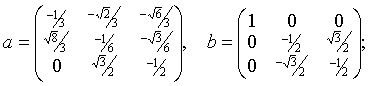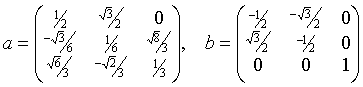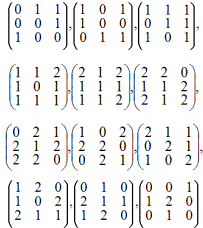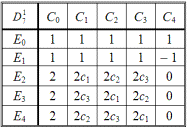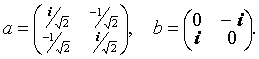Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.2. Группы на матрицах и подстановках

Представления групп тетраэдра, куба и икосаэдра

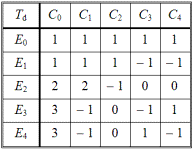
Группа тетраэдра T отличается от двух рассмотренных групп 20-го порядка. Характеры 4-х представлений выписаны в табл. 2.53.

Таблица 2.53

Рассмотрим трехмерное представление E₃ с четырьмя классами сопряженности C_i и нижеследующим базисом:

В представлениях E₁ и E₂ участвуют кубические корни из единицы — {1, ω, ω²}, представление E₃ состоит из двенадцати матриц:

Представление E₀ — единичное; E₁ и E₂ — гомоморфные, возникшие благодаря наличию в группе тетраэдра T нормального делителя N = {e, ab, ba, ab²a} типа . Соответствие между классами и представлениями здесь такое: E₀ ↔ C₀, E₁ ↔ C₂, E₂ ↔ C₃, E₃ ↔ C₁. Таким образом, на первый взгляд возникла необычная ситуация: класс коммутативных элементов C₁ породил изоморфное некоммутативное представление E₃, а два смежных класса некоммутативных элементов C₂ и C₃ отвечают двум коммутативным представлениям E₁ и E₂. Странным кажется и то, что восемь внешне одинаковых 3-цикла распались на два различных класса эквивалентности.

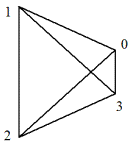
Рис. 2.9

Тетраэдр, который изображен на рис. 2.9, складывается из четырех равносторонних треугольников. Следовательно, он имеет четыре граневых оси третьего порядка, совпадающих с его вершинными осями, и три реберных оси второго порядка. Граневые оси дадут 8 элементов симметрии, вершинные — 3; добавив сюда один тождественный элемент, мы как раз и получим 12 элементов симметрии для этой геометрической фигуры.

Некоммутативную группу вращений тетраэдра ( T ) можно получить путем перемножения элементов двух коммутативных — C₃ и — с образующими: a = (012), x = (01)(23), y = (02)(13); при перемножении C₃ и будем иметь

T = {e, a, a²} · {e, x, y, xy} =

= {e, a, a², x, y, xy, a x, a²x, ay, a²y, axy, a²xy}.

С геометрической точки зрения, рассмотренная группа симметрии тетраэдра T не является полной. Ее можно увеличить в два раза, если произвести умножение группы тетраэдра T = C₃ · на группу C₂ = {e, z}, где в качестве образующего z выбрать транспозицию (01). Группа C₂ будет отвечать плоскости зеркальной симметрии, проходящей через две вершины (2, 3) и середину ребра (0, 1) (см. рис. 2.9). Эта зеркальная плоскость за счет осей симметрии размножится на шесть (по числу ребер), что приведет к появлению шести различных транспозиций. Комбинируя эти транспозиции между собой, получим еще шесть циклических подстановок четвертого порядка. Полная группа симметрии тетраэдра T_d будет состоять из 24-х элементов симметрии, которые приведены в табл. 2.54.

Таблица 2.54

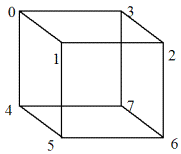
Тетраэдр можно вписать в куб (рис. 2.10), который имеет 6 квадратных граней с тремя осями четвертого порядка, 8 вершин с четырьмя осями третьего порядка и 6 реберных осей второго порядка. Таким образом, группа вращений куба (октаэдра) O складывается из следующих операций: вокруг каждой вершинной оси имеется два нетождественных поворота, до полного совмещения всех геометрических элементов куба; вокруг каждой граневой оси также имеется по три нетождественных поворота; наконец, существует по одному повороту вокруг реберных осей. После того, как мы добавим один тождественный поворот, получится полная группа вращений куба, в состав которой тоже входит 24 элемента, т.е. полная (с отражениями) группа симметрии тетраэдра T изоморфна группе вращений куба O. Добавим к сказанному, что в кубе, как и в тетраэдре, можно провести зеркальные плоскости, а также ввести центр симметрии, тогда число элементов в группе куба возрастет до 48.

Рис. 2.10

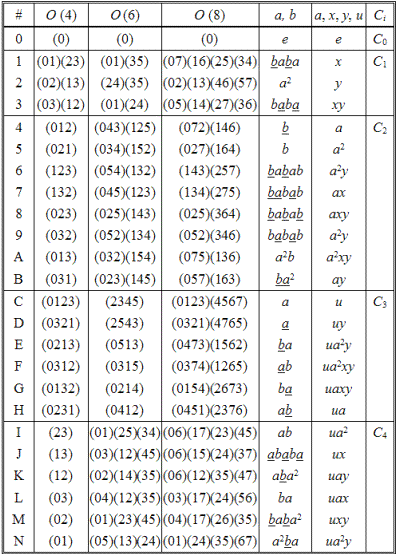
Если пространственные диагонали куба пронумеровать числами от 0 до 3, вершины куба — от 0 до 7, как показано на рис. 2.10, а грани куба — числами от 0 до 5 (причем грань 0123 как 0, 4567 как 1, 1256 как 2, 2367 как 3, 0347 как 4 и 0145 как 5), то будем иметь три системы изоморфных подстановок — O(4), O(6), O(8). Подстановки можно получить многими способами, в частности, как умножение группы тетраэдра ( T ) на одну из 6 циклических подстановок четвертого порядка (u), или как различные произведения двух образующих a и b. Упомянутые элементы симметрии приведены в табл. 2.54, в которой принято: a = a^–1 и b = b^{– 1}. Характеры пяти представлений полной группы симметрии тетраэдра T_d (группы вращений куба O) приведены в табл. 2.55.

Таблица 2.55

Образующими гомоморфного представления E₂ являются:

Образующие изоморфного представления E₃ —

и образующие изоморфного представления E₄—

Напомним, что группа T_d относится к симметрической — S₄, поэтому к ней применима методика диаграмм Юнга, которая использовалась нами для нахождения матриц неприводимых представлений группы S₃ = D₃, а также для определения размерности неприводимых представлений S₄ (рис. 2.8).

Таблицу характеров для представлений полной группы симметрии куба O_d можно получить путем учетверения табл. 2.55, т.е. использовать методику, которая применялась для составления таблиц характеров коммутативных групп (табл. 2.44) и C₂C₄ (табл. 2.45).

Перейдя от группы вращений тетраэдра T 12-го порядка к полной группе тетраэдра T_d 24-го порядка, мы, конечно, пропустили множество интересных групп, о которых необходимо сказать хотя бы несколько слов. На примере циклической группы 13-го порядка мы сделаем одно существенное замечание к матричным представлениям. Дело в том, что представления необязательно должны быть ортонормированными. Во вводном п. 2.1 для представления группы D₃ использовались матрицы с элементами, рассчитанными по mod (2), а для коммутативной группы C₆ — по mod (3). Следующие 12 матриц (без единичной) с элементами из целых чисел, взятых по mod (3), вполне представляют коммутативную группу C₁₃:

Эти матрицы интересны тем, что все они симметричны относительно неглавной (второй) диагонали. Однако никакого геометрического содержания в приведенных матрицах, по-вдмому, не заключено.

Ортонормированные представления любой диэдральной группы имеют вполне определенный геометрический смысл, поскольку группе диэдра можно поставить в соответствие действия над дипирамидами. Группа диэдра 14-го порядка здесь не является исключением. Неприводимые представления группы отличаются от аналогичных для группы (табл. 2.51) наличием третьего двухмерного представления E₄. Характеры представлений приведены в табл. 2.56, в которой константами c_i обозначены косинусы углов:

c₁ = cos (2π/7) = 0,6234

c₂ = cos (4π/7) = –0,2224

c₃ = cos (6π/7) = –0,9017

Таблица 2.56

Представления двух групп 16-го порядка и с одинаковыми таблицами характеров (табл. 2.57) строятся во многом по аналогии с представлениями групп и .

Таблица 2.57

Таблицы характеров двух других групп 16-го порядка, типа и , получаются путем учетверения таблицы характеров для групп и (табл. 2.48). Для группы 16-го порядка двухмерное изоморфное представление уже заметно отличается от всех ранее рассмотренных; его образующими являются матрицы:

Геометрический смысл для группы все еще сохраняется, поскольку базисные векторы (первые столбцы матриц) могут быть вычерчены в геометрическом пространстве с мнимой осью. 

Завершим рассмотрение симметрии геометрических фигур икосаэдром (рис. 2.11). Он имеет 20 треугольных граней, 30 ребер и 12 вершин, в каждой из которых сходятся по 5 ребер. Отсюда, очевидно, вытекает наличие у него 6 вершинных осей пятого порядка, 10 граневых осей третьего порядка и 15 реберных осей второго порядка. Несложный подсчет дает нам 60 элементов вращения. Группу симметрии икосаэдра (Y) можно получить, перемножая элементы группы вращений тетраэдра (T) на одну из циклических подстановок пятого порядка. Точно так же, как в группах тетраэдра и куба, число элементов симметрии икосаэдра удваивается за счет введения зеркальных отражений и центра симметрии.

Рис. 2.11

Напомним, что если центры граней правильных многогранников принять за вершины новых многогранников, то в тетраэдр, куб и икосаэдр можно вписать соответственно сопряженные тетраэдр, октаэдр и додекаэдр. Построенные таким образом геометрические фигуры относительно исходных называются двойственными. «Двойники» имеют ту же группу симметрии и систему подгрупп, что и исходные фигуры. Тетраэдр, гексаэдр (куб), октаэдр, икосаэдр и додекаэдр образуют пять Платоновых тел. Платон в своем сочинении "Тимей" атомам пяти элементов — огню, воздуху, воде, земле и эфиру — приписал форму этих пяти фигур.

Группа вращений икосаэдра Y не имеет нормальных делителей, т.е. в Y нет подгрупп, куда бы входили полные классы сопряженности. Если утверждается, что группа проста, значит, все ее представления будут изоморфными, одномерных представлений не будет, за исключением единичного E₀ (табл. 2.58). Константы p и q в табл. 2.58 те же, что и в табл. 2.51. 

Таблица 2.58

Критерий полноты набора неприводимых представлений дает единственно возможное разложение числа 60:

60 = 1² + 3² + 3² + 4² + 5² = 1 + 12 + 12 + 20 + 15.

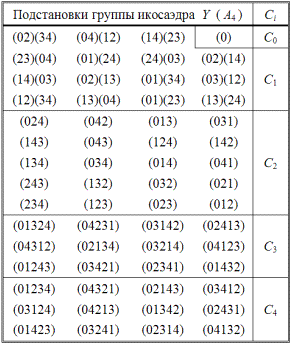
Клейн утверждает, что вращения икосаэдра периода 5 распадутся на два класса, в одном из которых окажутся повороты на угол ±2π/5, в другом — на угол ±4π/5. Теперь спросим себя: каким образом 24 подстановки «догадались» тоже разделиться на два класса по 12 подстановок в каждом; ведь подстановки ничего не «знали» о существовании икосаэдра? Тем не менее, обыкновенная процедура преобразования подобия приводит к тому, что одна часть 5-циклов попадает в класс C₃, другая — в класс C₄ (табл. 2.59). Следовательно, индексы подстановок удивительным образом обладают одинаковыми свойствами с вершинами, диагоналями и другими деталями икосаэдра. Оказывается, что в столь разнородные объекты, каковыми являются подстановки и геометрические фигуры, "вселился" один и тот же дух симметрии.

Таблица 2.59

И все-таки не настолько уж они единосущностны, как это может показаться вначале. Стоит ввести для икосаэдра плоскости симметрии, как тут же обнаруживается расхождение его симметрии с симметрией 120 подстановок, переставляющих всеми возможными способами 5 индексов, т.е. с симметрией группы S₅. Полная (с отражениями) группа симметрии икосаэдра не содержит в своем составе инвариантной подгруппы C₂, хотя подгруппа такого порядка там имеется. Геометрическая интерпретация есть проведение аналогии. Но всякое сравнение имеет свои границы: то, что справедливо для тетраэдра и икосаэдра как фигур вращения, уже неверно для них как фигур с элементами отражения.

Подгруппу четных подстановок в симметрической группе S_n часто называют знакопеременной и обозначают как A_n. У нас получилось следующее: знакопеременная подгруппа A₄ четных подстановок изоморфна группе вращения тетраэдра T; полная группа симметрических подстановок S₄ изоморфна полной группе симметрии тетраэдра T_d, т.е. переходы A₄ → S₄ и T → T_d эквивалентны. Что же касается икосаэдра, то здесь наблюдается иная картина: знакопеременная подгруппа A₅ четных подстановок также изоморфна группе вращений икосаэдра Y, но полная группа симметрических подстановок S₅ уже не изоморфна полной группе симметрии икосаэдра Y_d, т.е. переходы A₅ → S₅ и Y → Y_d не эквивалентны. Судя по описанию симметрии икосаэдра, сделанному Клейном, такое различие довольно трудно уловить человеческим воображением.