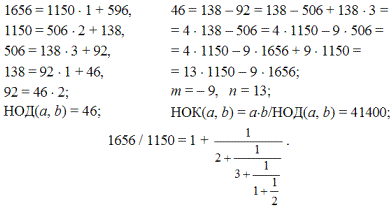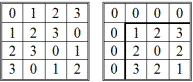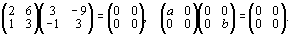Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.4. Алгебраические системы на базе групп

Сведения из теории чисел

Чтобы двигаться дальше, напомним некоторые общие сведения из теории чисел. Всякое натуральное число p, не имеющее других натуральных делителей, кроме единицы и самого себя, называется простым, в противном случае — составным (единица считается ни простым, ни составным). Всякое натуральное число a, кроме единицы, может быть представлено произведением простых множителей: a = p₁p₂ ... p_n. Среди простых сомножителей этого представления могут встретиться равные. Если через p₁, p₂, ..., p_k обозначить различные простые числа и допустить, что они встречаются, соответственно, n₁, n₂, ... , n_k раз, то получим представление a = p₁ⁿ¹ p₂ⁿ² ....p_k^nk, которое называется каноническим. Так, каноническое разложение числа 360 выглядит следующим образом: 2³3²5. Каноническое разложение показывает, что все делители числа a исчерпываются числами вида

d = p₁^m1p₂^m2 ... p_k^mk,

где 0 ≤ m₁ ≤ n₁, 0 ≤ m₂ ≤ n₂, ... , 0 ≤ m_k ≤ n_k .

Отношение делимости не является отношением эквивалентности: a/b ≠ b/a, но операция сравнения по mod(m) будет такой, поскольку для нее выполняются все три закона эквивалентности: a = a mod(m) — рефлексивности, из a = b mod(m) следует b = a mod(m) — симметричности, если a = b mod(m) и b = c mod(m), то a = c mod(m) — транзитивности.

Вычеты по mod(m) определяют разбиение множества целых чисел на m классов эквивалентности: 

{C₀, C₁, C₂, ... , C_m–1},     где C_i = {i, i + m, i + 2m, ...}. 

Например, для неотрицательных целых чисел по mod (4) имеется четыре класса:

C₀ = {0, 4, 8, 12, ...},     C₂ = {2, 6, 10, 14, ...},

C₁ = {1, 5, 9, 13, ...},     C₃ = {3, 7, 11, 15, ...}.

Объединение непересекающихся классов дает бесконечный монотонно возрастающий числовой ряд. Классы образуют фактормножество, которое может быть представлено в нашем случае четырьмя представителями — {0, 1, 2, 3}; представители образуют ядро этого фактормножества. Для представителей можно ввести операции сложения и умножения по mod(4), которые удобно оформить таблицами (табл. 2.70 и табл. 2.71).

Таблица 2.70       Таблица 2.71

По сложению (табл. 2.70) имеем коммутативную группу, а по умножению (табл. 2.71) — нет, так как у нас получилось 2 · 2 = 0, что не допустимо для группы, но допустимо для кольца, которое имеет делители нуля. Примером кольца с делителем нуля является кольцо квадратных матриц:

Кольца без делителей нуля называются кольцами целостности.

Если вычеты образованы по модулю простого числа, то фактормножество или ядро его представителей является полем GF(p), которое имеет специальное название — поле Галуа. В этих полях делители нуля уже отсутствуют, поэтому они занимают особое место в алгебре. Отбросив окаймляющие нули в таблице умножения для полей Галуа, которые есть и в табл. 2.71, мы получим элементы, образующие циклическую группу. Табл. 2.72 и табл. 2.73 являются примерами группового сложения и умножения в поле Галуа GF(5).

Таблица 2.72          Таблица 2.73

При работе с полями многочленов нам понадобятся понятия наибольшего общего делителя двух чисел a и b — НОД(a, b) и наименьшего общего кратного — НОК(a, b), а также алгоритм Евклида. Напомним их содержание с помощью конкретного примера. Пусть даны два числа a = 24 и b = 30. Выпишем все делители этих чисел —

d(24) = {1, 2, 3, 4, 6, 8, 12, 24},  d(30) = {1, 2, 3, 5, 6, 10, 15, 30}.

Совокупность общих делителей образует множество {1, 2, 3, 6}. Следовательно, наибольший общий делитель равен 6. При больших числах для разыскания НОД используют алгоритм Евклида. Его содержание сводится к последовательному вычислению следующих равенств:

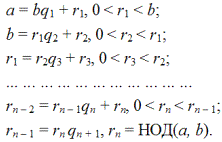
Действие алгоритма прекращается тогда, когда полученный остаток равен нулю; последний ненулевой остаток (r_n) равен наибольшему общему делителю. Как следствие, из алгоритма Евклида вытекает, что для любых целых чисел a и b всегда существуют такие числа m и n, что НОД(a, b) представляется в виде линейной комбинации этих чисел:

ma + nb = r_n = НОД(a, b).

Кроме того, отношение a/b можно представить в виде цепной дроби. Чтобы к ней перейти, разделим все равенства, полученные в алгоритме Евклида, на b, r₁, r₂, ..., r_{n –1}, r_n, получим:

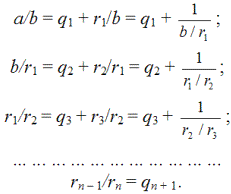
Последовательно подставляя эти равенства друг в друга, получаем цепную дробь: