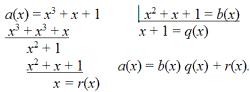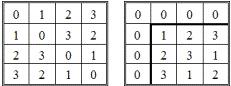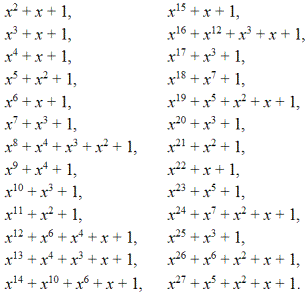
Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.4. Алгебраические системы на базе групп

Поля многочленов

Теперь мы приобрели необходимые сведения для действия и с многочленами n-ой степени вида:

a_n(x) = a₀xⁿ + a₁x^n–1 + ... + a_n–1x + a_n.

Если a_n(c) = 0, то c — корень многочлена a_n(x). Число c будет корнем a_n(x) тогда и только тогда, когда a_n(x) делится на скобку (x – c) без остатка. Действительно, пусть

a(x) = (x – c)b(x) + r(x)

при x = c, имеем a(c) = (c – c)b(c) + r(c). Таким образом, остаток r(c) = a(c), который равен нулю по определению.

Поиск корней многочлена a_n(x) равносилен поиску его линейных делителей; при a₀ = 1 получим

a_n(x) = (x – c₁)b₁(x) = (x – c₁)(x – c₂)b₂(x) = ...

= (x – c₁)(x – c₂) ... (x – c_n).

Общее число корней многочлена a_n(x) всегда равно n. Однако могут встречаться кратные корни, тогда

a_n(x) = (x – c₁)ⁿ¹(x – c₂)ⁿ² ... (x – c_k)^nk.

Это называется каноническим разложением многочлена a_n(x) на простые (неприводимые) множители. Многочлен a(x) называется приводимым, если он может быть разложен в произведение двух множителей без остатка —

a(x) = b(x)q(x).

Но известна ситуация, когда многочлен a(x) часть корней имеет в поле действительных чисел, а часть — в поле комплексных чисел. Таким образом, о приводимости или неприводимости многочленов можно говорить лишь по отношению к данному полю, поскольку многочлен, неприводимый в одном поле, может оказаться приводимым в другом. Ранее приведенный пример с многочленом x³ – 1 в этом отношении показателен.

Далее нас будут интересовать многочлены a(x), у которых коэффициенты a_i взяты из числового поля GF(p). Эти многочлены образуют кольцо относительно сложения и умножения. Пусть этими многочленами будут

a(x) = x³ + x + 1         и         b(x) = x² + x + 1,

а числовое поле GF(2) = {0, 1}, тогда сумма и произведение a(x) и b(x) дадут два новых многочлена —

a(x) + b(x) = x³ + x²         и         a(x) · b(x) = x⁵+ x⁴ + 1.

В своей совокупности многочлены образуют именно ассоциативно-коммутативное кольцо, но не поле, поскольку не существует таких многочленов степени больше единицы, которые бы при перемножении давали единицу: a(x) · b(x) = 1, т.е. в алгебре многочленов для каждого ее элемента отсутствует обратный.

Многочлены можно делить друг на друга:

Многочлен b(x) называется делителем a(x), если остаток r(x) равен нулю. Наибольший общий делитель двух многочленов a(x) и b(x) находится по алгоритму Евклида, только роль чисел уже выполняют многочлены. Покажем, как его найти на многочленах a (x) и b(x) с коэффициентами, взятыми из числового поля GF(3):

a(x) = x⁶ + 2x³ + x² + 2x + 2,       b(x) = x⁵ + x⁴ + x³ + x² + x + 1.

Следуем алгоритму Евклида:

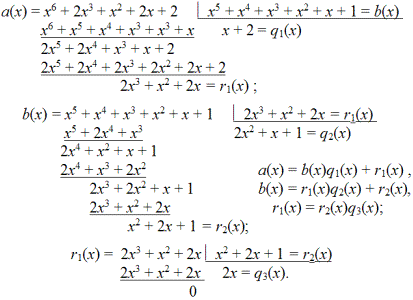
Таким образом, НОД(a(x), b(x)) = x² + 2x + 1 = r₂(x). Чтобы найти НОК, необходимо знать результат от перемножения исходных многочленов; он равен:

a(x)b(x) = x¹¹ + x¹⁰ + x⁹ + x⁷ + x⁵ + x⁴ + x³ + 2x² + x + 2;

НОК(a(x), b(x)) = a(x)b(x) / НОК(a(x), b(x)) =

= x⁹ + 2x⁸ + 2x⁷ + 2x⁵ + 2x⁴ + x³ + 2.

Коэффициенты m(x) и n(x) линейного разложения НОД (a(x), b(x)) по a(x) и b(x) равны:

m(x) = x³ + 2x² + x,       n(x) = 2x⁴ + 2x³ + x² + x + 1.

Для многочлена, как и для чисел, можно ввести сравнение многочлена a(x) по модулю многочлена q(x): a(x) = r(x) mod q(x). А раз так, то можно говорить и о поле многочленов GF(q) над числовым полем GF(p). Если GF(2), а q(x) = x³ + 1, то имеем поле многочленов GF(x³ + 1), состоящее из восьми многочленов: 

{0, 1, x, x + 1, x², x² + 1, x² + x, x² + x + 1}. 

Здесь p = 2 называется характеристикой поля GF(p); характеристика определяет размерность или порядок полей многочлена: q = pⁿ = 2³ = 8, где n — степень многочлена q(x). Перемножим два произвольных элемента поля GF(q) по mod q(x): 

(x² + 1) x² = x⁴ + x² = x(x³ + 1) + (x² + x) = x² + x.

Продолжая далее перемножать элементы GF(q), мы могли бы составить таблицу умножения. Но мы составим таблицы сложения (табл. 2.74) и умножения (табл. 2.75) для другого поля многочленов — GF(x² + x + 1), размерность которого в два раза меньше: {0, 1, x, x + 1}. Каждому элементу последнего множества можно поставить в соответствие либо двоичное число: {00, 01, 10, 11}, либо десятичное: {0, 1, 2, 3}, тогда таблицы сложения (табл. 2.74) и умножения (табл. 2.75) поля GF(x² + x + 1) предстанут в виде числовых таблиц (табл. 2.76) и (табл. 2.77), схожих с табл. 2.70 и табл. 2.71.

Таблица 2.74         Таблица 2.75

Таблица 2.76         Таблица 2.77

Обращаем внимание читателя на тот примечательный факт, что табл. 2.77 по сравнению с табл. 2.71 не имеет делителя нуля, а три элемента, отличных от 0, образуют циклическую группу; другими словами, множество GF(x² + x + 1), состоящее из четырех элементов, образует поле Галуа. Напомним, что выше числовое поле Галуа GF(p) могло получиться только для простых чисел: p = 2, 3, 5, 7, ... . У нас же q = pⁿ = 2² = 4, а поле получилось как от простого числа. В литературе [46, п. 4.2; 77, с. 252 — 256] показано, что поля Галуа возникают тогда, когда число элементов q равно степени простого числа; или, иначе, GF(q) будет полем Галуа, когда q(x) является простым (неприводимым) многочленом. Приведем по одному простому многочлену степени 2 — 27:

Циклическая группа по умножению (табл. 2.75) изоморфна циклической группе корней кубических из единицы (табл. 2.69), только в качестве элементов в данном случае выступают многочлены: c₁ = 1, c₂ = x, c₃ = x + 1, получающиеся за счет расширения числового поля, подобное расширению числового поля действительных чисел за счет комплексных. Если в качестве образующего взять элемент c₂ = x, то последовательным возведением его в первую, второю и третью степень получим все три элемента: x¹ = x, x² = x + 1, x³ = 1. Эти элементы являются корнями уравнения

x³ + 1 = (x + 1)(x² + x + 1) = 0,

решенного в поле GF(2).

Приведем примеры таблиц сложения и умножения для следующих полей многочленов:

GF(3²) = {0, 1, 2, 3, 4, 5, 6, 7, 8} =

= {0, 1, 2, x, x + 1, x + 2, 2x, 2x + 1, 2x + 2},

с порождающим многочленом g(x) = x² + x + 2; таблица сложения — табл. 2.78, таблица умножения — табл. 2.79.

Таблица 2.78

Таблица 2.79

GF(2⁵) = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} =

= {0, 1, x, x + 1, x², x² + 1, x² + x, x² + x + 1, x³, x³ + 1, x³ + x,

x³ + x + 1, x³ + x², x³ + x² + 1, x³ + x² + x, x³ + x² + x + 1},

с порождающим многочленом g(x) = x⁴ + x³ + 1; таблица сложения — табл. 2.80, таблица умножения — табл. 2.81.

Таблица 2.80

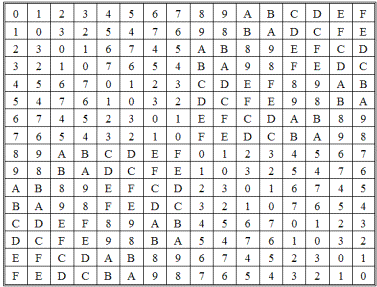
Таблица 2.81

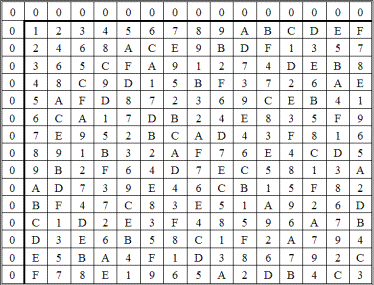
Все выписанные таблицы определяют знакомые нам коммутативные группы. Если по таблицам составить регулярные подстановки, то их структура сразу же будет узнаваема. Естественно, для этих групп можно найти все их подгруппы, включая нормальные делители. Та роль, которая в группах принадлежит нормальным делителям, в кольцах принадлежит идеалам. Подмножество I кольца K называется идеалом, если оно является подгруппой аддитивной группы кольца. Для того чтобы подмножество I было идеалом в K, необходимо выполнение единственного условия, а именно: если i ∈ I и k ∈ K, то их произведения ik и ki должны принадлежать подмножеству I. Если в определении идеала отказаться от требования, что оба произведения ik и ki принадлежат I, то придем к понятию одностороннего идеала: если ik ∈ I — правый идеал, если ki ∈ I — левый идеал. Всякий идеал кольца будет подкольцом. Пересечение любой системы идеалов кольца будет идеалом.

В кольцах Ли и Ёрдана левые и правые идеалы совпадают; такие идеалы называются двухсторонними. Из определения идеала следует, что во всяком кольце K идеалами являются само кольцо K и так называемый нуль-идеал, состоящий из одного нулевого элемента. Кольцо, не содержащее других идеалов, кроме этих двух, называется простым. Все тела и поля являются простыми кольцами.

Можно было бы продолжать вводить для колец и полей понятия гомоморфизма, фактормножества и т.д., только все это нас слишком уведет в сторону. Между тем, овладев техникой анализа групп, провести подобный анализ для полей не составит большого труда. Поэтому вернемся непосредственно к многочленам.