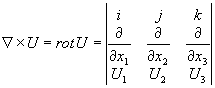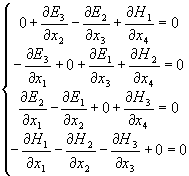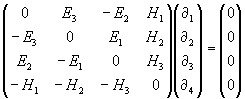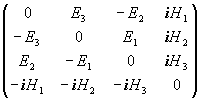Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.5. Пространственные группы и двойственность

Симметрия уравнений Максвелла

К важнейшей группе пространственных преобразований относятся преобразования Лоренца, оставляющие без изменения (инвариантными) электромагнитные уравнения Максвелла и волновое уравнение. В лоренцевых преобразованиях участвуют три координаты пространства (x₁, x₂, x₃), одна координата времени (x₄ = ct) и два параметра: переменный параметр скорости (v) и одна постоянная скорость (c). Уравнения Максвелла сводятся к волновому уравнению, но прежде чем мы это сделаем, установим связь электромагнитных уравнений с алгеброй Клиффорда.

Примерами внутреннего (скалярного) и внешнего (векторного) произведений являются дивергенция и ротор:

       

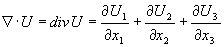
Определим вектор напряженности электрического поля (E), как градиент скалярного потенциала (φ) и бивектор напряженности магнитного поля (H) как ротор векторного потенциала (a):

E = – grad φ = – i – j – k,       H = rot a.

Тогда через клиффордово произведение можно дать все четыре уравнения Максвелла для статического электромагнитного поля:

∇(E + H) = ∇×E + ∇×H + ∇·E + ∇·H.

Распишем уравнение по составляющим, присвоив первому члену значение плотности заряда (ρ), а последнему — величину тока (j):

∇×E = div E = ρ — скаляр,       ∇×H = div H = 0 — вектор,

∇·E = rot E = 0 — бивектор,       ∇·H = rot H = j — псевдоскаляр.

Обратим внимание на то, что было бы странно в списке уравнений Максвелла иметь, скажем, пять уравнений. В этом случае было бы непонятно, какой математической модели подчиняются электромагнитные явления.

Для динамического случая изменение магнитного поля приводит к возникновению ротора электрического поля, а изменение электрического поля — ротора магнитного поля. Уравнения Максвелла примут вид:

div E = ρ,       div H = 0,       rot H – = j,        rot E + = 0.

Они же, расписанные по четырем составляющим:

,    

Они же, но уже в матричной форме:

,    

Здесь принято, что ∂_i = ∂/∂x_i, ct = x₄ и j = ρv или подробно:

(j₁, j₂, j₃, j₄) = ρ(∂x₁/∂x₄, ∂x₂/∂x₄, ∂x₃/∂x₄, ∂x₄/∂x₄,)

Представленный вид уравнений Максвелла позволяет увидеть, что электрическая и магнитная составляющие не образуют целиком самодвойственную систему, так как математические выражения относительно этих величин не совсем симметричны. Физические же эксперименты, как показал Ленц, демонстрируют полную дуальность электромагнитных и магнитоэлектрических явлений. Чтобы достичь идеальной двойственности, необходимо в уравнения Максвелла ввести мнимость. Тогда две выписанные выше матрицы предстанут в ином виде:

     

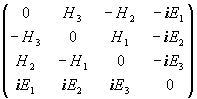
Без мнимой единицы уравнения Максвелла неполны: они многое теряют в своей геометрической и физической интерпретации.