Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.5. Пространственные группы и двойственность

Двойственность и проецирование

Рассмотренная ранее группа проективных преобразований (z' = 1/z)касается уравнения линии и окружности. Группа преобразований плоскости имеет вид:

, при этом Δ = ≠ 0

Группа всех трехмерных проективных преобразований состоит из системы трех уравнений; ее подгруппой будет система трехмерных аффинных преобразований; выпишем их соответственно:

, , ≠ 0

Во всех пространствах проективной геометрии действует принцип двойственности, но он отсутствует в аффинных пространствах или более узком их классе — евклидовых пространствах. Различие между аффинным и евклидовым пространствами состоит в следующем: если в аффинном пространстве вводится понятие о векторах и их сумме, то для евклидова пространства вводится также понятие скалярного произведения векторов как суммы произведений их соответствующих координат. При аффинных преобразованиях прямые всегда переходят в прямые, причем сохраняется их взаимное расположение: пересекающиеся переходят в пересекающиеся, скрещивающиеся — в скрещивающиеся, а параллельные — в параллельные. Для проективных пространств, как было сказано, справедлив принцип двойственности, действие которого было продемонстрировано на примере самого элементарного проективного преобразования — z' = 1/z.

Говорят, что точка и прямая инцидентны, если точка лежит на прямой (или прямая проходит через точку); аналогично говорят о точке и плоскости или прямой и плоскости. Пользуясь этим термином, принцип двойственности можно сформулировать следующим образом: если справедлива некоторая теорема T, в которой говорится что-либо об инцидентности точек, прямых и плоскостей трехмерного проективного пространства, то будет справедлива и двойственная теорема T ', которая получается из T заменой термина точка на термин плоскость и плоскость на точку, термин прямая остается без изменений. Для двумерной проективной геометрии на плоскости точка заменяется на прямую, а прямая — на точку. Две школьные аксиомы: две прямые пересекаются в одной точке и через две точки можно провести единственную прямую связаны принципом двойственности. Фактически текст теорем в результате действия принципа двойственности подвергается большему изменению, так как надо заменять слова вписанная кривая на описанная кривая, расстояние между двумя точками на угол между прямыми и т.д. Но логическая канва двойственных теорем абсолютно идентична. Продемонстрируем действие принципа двойственности на проективной плоскости, для чего сформулируем две теоремы.

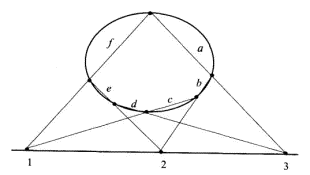
Теорема Паскаля. Каким бы ни был шестиугольник, вписанный в линию второго порядка (например, эллипс), точки пересечения его противоположных сторон лежат на одной прямой P (рис. 2.36а).

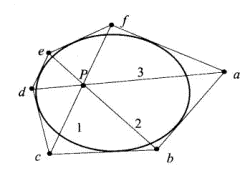
Теорема Брианшона. Каким бы ни был шестиугольник, описанный вокруг линии второго порядка, прямые, соединяющие его противоположные вершины, проходят через одну точку P (рис. 2.36б).

P

Рис. 2.36

Появились эти две теоремы с интервалом в сто лет. Между тем, они находятся в отношении двойственности и имеют абсолютно одинаковую логическую структуру. Стоит поменять ключевые термины (вписанный — описанный, точка — прямая) на двойственные, как тут же обнаружится их эквивалентность.

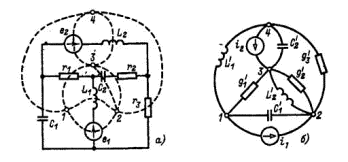
Принцип двойственности, действующий в проективных пространствах, правильнее назвать самодвойственным или автодвойственным, так как одно множество элементов проективного пространства проецируется на другое множество этого же проективного пространства (z' = 1/z). Типичный пример такой двойственности мы находим в электротехнике; при этом производят следующую замену слов: источник тока — источник э.д.с., сопротивление — проводимость, индуктивность — емкость, последовательное соединение элементов — параллельное соединение элементов. На рис. 2.37а приведена исходная электрическая цепь, а на рис. 2.37б — двойственная ей, которая вычерчивается в соответствии с двойственным графом.

Элементы обеих цепей находятся в следующем отношении: сопротивлениям (r) первой цепи отвечают проводимости (g') второй, индуктивности (L) соответствуют емкостям (C'), и наоборот, а напряжения (u) – токам (i'), так что можно написать следующие взаимно однозначные соответствия:

, , ;

, , .

Рис. 2.37

Комплексное сопротивление (Z) первой цепи соответствует комплексной проводимости (Y') второй цепи:

, , .

где k — коэффициент пропорциональности.

Но электромагнитным величинам можно поставить в соответствие не магнитоэлектрические, а механические величины, имеющие совершенно иную природу; в этом случае говорят уже о проецировании одной системы физических величин на другую. Проецирование можно осуществить внутри классической механики, но так, чтобы не возникало автоморфизма или автопроецирования. В табл. 2.91 приведены такие соответствия между механическими и электромагнитными величинами, с одной стороны, и между механическими величинами поступательного движения и механическими величинами вращательного движения, с другой стороны.

Таблица 2.91

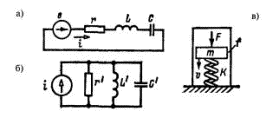
№	Электротехника	Механика перемещения	Механика вращения
1	Напряжение u [В]	Сила F [Н]	Момент M [Н×м]
2	Заряд q [Кл]	Линейное перемещение x [м]	Угловой поворот φ [рад]
3	Ток i [А]	Линейная скорость v [м/с]	Угловая скорость ω [рад/с]
4	Индуктивность L [Г]	Масса m [кг]	Момент инерции J [кг × м2]
5	Емкость C [Ф]	Податливость K –1 [м/Н]	Податливость G –1 [рад/(Н×м)]
6	Сопротивление r [Ом]	Коэф. трения перемещ. f [кг/с]	Коэф. трения вращен. k [кг × м2/с × рад]
7	Магнитн. энергия Li2/2 [Дж]	Кинет. энерг. перемещ. mv2/2 [Дж]	Кинетич. энергия враще. Jω2/2 [Дж]
8	Электрич. энергия Cu2/2 [Дж]	Потен. энергия перемещ. Kx2/2 [Дж]	Потенц. энергия вращ. Gφ2/2 [Дж]
9	Мгнов. мощность ui [Вт]	Мощн. перемещ. Fv [Вт]	Мощн. вращен. Mω [Вт]
10	Мощн. рассеяния ri2 [Вт]	Трение от перемещ. fv2 [Вт]	Трение от вращ. kω2 [Вт]

Для электроцепи (рис. 2.38а), куда последовательно включены источник электродвижущей силы (e), активное сопротивление (r), катушка индуктивности (L) и емкость (C), будем иметь следующее уравнение для напряжений:

.

Рис. 2.38

Двойственная (автоморфная) цепь будет представлять собой контур с соответствующими элементами, включенными параллельно (рис. 2.38б). Уравнение для токов этой цепи выглядит так:

.

Но электрическим цепям можно поставить в соответствие изоморфную механическую конструкцию, состоящую из цилиндра, установленной внутри него пружины (с величиной упругости K), к которой крепится поршень массой m (рис. 2.38в). Если на поршень действует сила F, разгоняющая его до скорости v, то с учетом коэффициента трения f получим динамическое уравнение классической механики, изоморфное к двум первым уравнениям:

.

Подобного рода проецирование можно рассматривать как расширение принципа двойственности, который выходит за пределы одного физического пространства и находит себе взаимно однозначные элементы совершенно в другом физическом пространстве. Таким образом, двойственность проявляется в способности того или иного преобразования создавать однозначно связанные пары или соответствия, которые рассматриваются как взаимные проекции элементов одного множества на элементы другого. Один из примеров такого соответствия, когда элементы, принадлежащие одному пространству, проецируются на элементы другого, рассмотрим подробно.