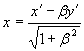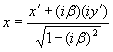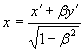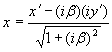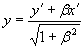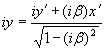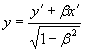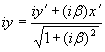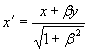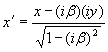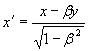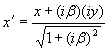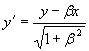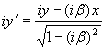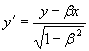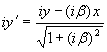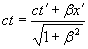Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.5. Пространственные группы и двойственность

Ортогональные и гиперболические преобразования

Взгляните на табл. 2.92, где приведены полные системы ортогональных и гиперболических поворотов. Сами повороты координатных осей образуют две различные группы преобразований, действующие в евклидовом и псевдоевклидовом пространствах. Каждая из этих групп состоит из пары прямых и пары обратных преобразований на плоскости. Однако четыре ортогональных преобразования можно спроецировать на четыре гиперболических, а четыре гиперболических — на четыре ортогональных; для этого нужно только ввести мнимую единицу для оси ординат. Таким образом, вся система проецирования указанных преобразований построена на одном очень простом преобразовании оси y:

y → iy.

Таблица 2.92

Ортогональные преобразования		Гиперболические преобразования
Ортогональный поворот осей	Гиперболический поворот осей	Гиперболический поворот осей	Ортогональный поворот осей

Сейчас нас будет интересовать один вопрос — изменение масштабов длины для ортогональных и гиперболических преобразований. При ортогональном повороте декартовых координат масштабы длины не изменяются, при гиперболическом повороте масштабы изменяются, но преобразование y → iy и β → –iβ (так как –iβ = x/iy) превращает ортогональный поворот в гиперболический, а гиперболический — в ортогональный. Ставится задача найти пересчетную формулу для координат гиперболических преобразований, которые являются, как известно, преобразованиями Лоренца. Чтобы соблюсти устоявшуюся в физике форму представления гиперболических преобразований, мы везде обозначаем ось ординат не через y, а через ct. Сначала рассмотрим ортогональный поворот декартовых координат, затем — гиперболический.

Если точку A (рис. 2.39а) выбрать на окружности единичного радиуса, то формулам пересчета из одной декартовой системы в другую будут отвечать формулы синуса и косинуса суммы двух углов:

cos(φ + ψ) = cosψ cosφ – sinψ sinφ, 

sin(φ + ψ) = cosψ sinφ + sinψ cosφ.

Непосредственно из чертежа видно, что

cosψ = x',     sinψ = ct',     cos(φ + ψ) = x,     sin(φ + ψ) = ct.

Следовательно,

x = x'cosφ – ct'sinφ,     ct = x'sinφ + ct'cosφ.

Так как

tgφ = x_B /ct_B = v/c = β, cosφ = , sinφ = ,

окончательно получаем первые две формулы ортогонального преобразования в форме ортогонального поворота, который соответствует первым двум формулам первого столбца табл. 2.92:

    

    .

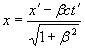
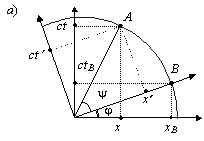
Рис. 2.39

Последние формулы могут быть переписаны в гиперболической форме, тогда масштабы осей абсциссы и ординаты изменятся, несмотря на присутствие мнимой единицы. Обычно измененные масштабы ищутся путем обнуления одной из координат. Например, чтобы найти изменившуюся длину Δx' штрихованной системы по известной длине Δx нештрихованной (ортогональной) системы, берут координаты двух точек на оси абсцисс и составляют из них разность:

,     ,     .

При условии одновременного измерения пространственных координат, т.е. выполнения условия t₁ = t₂, получается формула сокращения длины:

.

Аналогичная методика нахождения соотношения между масштабами штрихованной и нештрихованной систем координат должна срабатывать и для ортогональных преобразований декартовых координат:

,     ,     .

При условии t₁ = t₂ получим формулу удлинения длины:

.

Но при повороте декартовых координат масштабы, как известно, не меняются. В действительности полученное соотношение

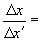
= cosφ

указывает лишь на косинус угла поворота осей. Каким же образом нужно поступать, чтобы рассчитать соотношение между масштабами штрихованной и нештрихованной систем координат при гиперболическом повороте, который показан на рис. 2.39б?