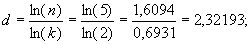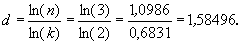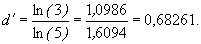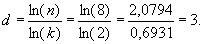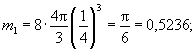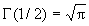
Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

4.3. К вопросу о размерности

Фрактальное строение живой и неживой природы — все это, конечно, очень любопытно, но нас сейчас интересуют математические аспекты. В частности, у читателя наверняка созрел вопрос относительно пространственной размерности. В каком смысле говорилось о дробной размерности в начале этого подраздела и в каком смысле эта дробная размерность касается трехмерных и двухмерных губок, изображенных на рис. 4.6 и 4.7?

Чтобы не вводить читателя в заблуждение, ему с самого начало необходимо объяснить, что фрактальная размерность — понятие искусственное, которое ничего общего не имеет с реальной размерностью физического мира. Не нужно путать также размерность пространства с его связанностью. Топологическая связанность, как мы знаем (п. 3.6), выражается целыми числами, причем связанность плоскости и шара одна и та же, хотя шар — математический объект трехмерного пространства, а плоскость — двухмерного. Тор и «кренделя» существуют в трехмерном мире, их высокая целочисленная величина связанности позволяет планарным образом уложить на их поверхности непланарные на шаре графы. Размерность пространства, как и связанность, может быть только целочисленной величиной. Фрактальная размерность тоже может оказаться целочисленной, однако некоторые авторы, следуя традиции, целочисленную размерность за фракталами не признают. Этот факт делает прекрасную ломаную Пеано, удовлетворяющую свойствам фрактала, нефрактальной. Познакомимся с ней поближе.

В 1890 г. итальянский математик Джузеппе Пеано (1858—1932), исследуя вопросы теории континуальных множеств, решил построить линию, которая отвечала бы точкам плоскости. Если взять единичный квадрат, разделить его на девять частей и затем обойти все эти части по маршруту, указанному на рис. 4.8а, то будем иметь настоящий паттерн с размерностью d = 2, т.е. той же, что и у плоскости. В том, что это действительно паттерн, убеждают два рисунка (рис. 4.8б и 4.8в), на которых показана диаграмма, отвечающая следующему набору величин:

k = 3, n = 9, h = 4 и φ = {0 1 0 3 2 3 0 1 0}.

Для удобства записи векторов единичная площадка, изображенная на рис. 4.8а, на двух следующих рисунках (рис. 4.8б и 4.8в) повернута так, чтобы направление начала обхода совпало с горизонтальным направлением оси абсцисс. 

Исходный квадрат можно разбивать не на 9 квадратиков, а на 4. В этом случае размерность не изменится (d = 2), но обход квадратиков и, следовательно, правила рекурсии поменяются в соответствии с новой конфигурацией, развитие которой можно проследить на рис. 4.9 (а, б, в и д). Вся плоскость может быть разделена не на квадраты, а на треугольники, как это показано на рис. 4.9г. Тогда внешний вид фрактала замет но изменится (рис. 4.9е). Обход разбитой на части плоскости можно организовать совершенно иначе (рис. 4.9ж), но размерность фрактала не изменится. Если существует фрактал с целочисленной размерностью d = 2, то аналогичным путем можно получить объемный фрактал с целочисленной размерностью d = 3. Отказываться зачислять кривые, наподобие ломаной Пеано, в разряд фракталов только потому, что у них целочисленная размерность, было бы не совсем разумно. Поэтому вполне понятно, что ломаная Пеано, так или иначе, рассматривается практически всеми авторами, пишущими о фракталах

а     б     в    

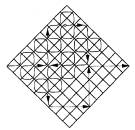
Рис. 4.8

а     б     в     г

д     е     ж

Рис. 4.9

На рис. 4.10а показан линейный фрактал, заданный параметрами: k = 2, n = 5, h = 3 и φ = {0 0 1 2 0}. Размерность этого фрактала равна

второй вектор равен

φ₂ = {0 0 1 2 0} × {0 0 1 2 0} = {00120 00120 11201 22012 00120};

В соответствии с φ₂ можно построить первые две пирамиды, причем некоторые отрезки ломаной придется проходить по два раза. Вся целиком ломаная, изображенная на рис.4.10а, соответствует пятому шагу (m = 5), т.е. вектору φ₅.

а     б

в     г     д

Рис. 4.10

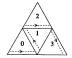
Однако похожую структуру, изображенную на рис. 4.10а, дают многие фракталы, в основе которых лежат самые различные паттерны. На рис. 4.10б изображено троичное дерево при m = 5; его граф-паттерн легко вычленить из дерева с m = 2, показанного на рис. 4.10в. Несложно с помощью компьютерной программы этот граф-паттерн заставить расти подобно живому папоротнику или ледяному узору на оконном стекле в морозную погоду — именно такие ассоциации приходят в голову, когда смотришь на рис. 4.10б. С каждым шагом сторона равностороннего треугольника или его высота удваиваются, т.е. k = 2, но число элементов, из которого состоит данный паттерн, равно трем (n = 3). На последних двух рис. 4.10 показаны схемы выстраивания аналогичных пирамид из равносторонних треугольников (г) и квадратов (д), для которых масштабный коэффициент и число элементов паттерна определяется теми же числами — k = 2, n = 3. Треугольники, изображенные на рис. 4.10г, мало чем отличаются от треугольника, показанного на рис. 4.7. Мы знаем, что любой плоский треугольник, с точки зрения геометрии, имеет пространственную размерность, равную двум; ломаная кривая, какая бы она ни была, имеет геометрическую размерность, равную единице; а объемные фигуры, вроде губки Менгера, изображенной на рис. 4.6а, имеют размерность, равную трем. Но что у нас получается, когда мы начинаем подсчитывать размерность по формуле Хаусдорфа? Для явно плоских объектов, какими являются фигуры, изображенные на рис. 4.7 или 4.10 (г) и (д), формула дает следующее дробное число:

Числа d = 2,32193 (подсчитанное в общем-то для одномерной геометрической фигуры, показанной на рис. 4.10а) и d = 1,58496 различаются заметно. Чтобы не создавать путаницы в размерности, нужно разделить геометрическую и фрактальную размерность. Пирамида, выстроенная наподобие карточного домика, была предложена польским математиком Вацловом Серпинским (1882 — 1969) в 1915 г. в связи с его исследованиями в области теории множеств. Сейчас эту конструкцию часто называют ковром или салфеткой Серпинского. В дальнейшем при построении ковра Серпинского мы применим преобразование подобия или аффинное преобразование, размерность которого определяется числом переменных. Это преобразование может увеличивать или уменьшать площадь геометрического объекта, поворачивать или переносить его с места на место, но оно никак не влияет на пространственную размерность этого объекта.

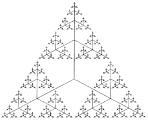
Главным идеологом теории множеств был Георг Кантор (1845 — 1918). Он в 1883 г. предложил алгоритм построения бесконечного множества отрезков, которые до этого, в 1875 г. рисовал еще Генри Смит. Сейчас это множество называется пылью Кантора; алгоритм получения канторовской пыли показан на рис. 4.11а. Нам ничего не стоит слегка изменить этот алгоритм, а именно, делить каждый отрезок не на три части, а на пять и выбрасывать не одну долю, а две, как это показано на рис. 4.11б. Для канторовской пыли имеем k = 3, n = 2, для вновь полученной — k = 5, n = 3; значит, существует и две различные размерности:

   

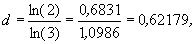
И вновь зададимся тем же самым вопросом, какая принципиальная разница заключена в этих двух рисунках? Очевидно, никакой, значит, ее нет и для порождающих векторов и для фракталов, изображенных на рис. 4.11а —

φ₁ = {101}, φ₂ = {101 000 101}, φ₃ = {101 000 101 000 000 000 101 101 101} ...

и на рис. 4.11б — φ'₁ = {10101}, φ'₂ = {10101 00000 10101 00000 10101}, ...

а          б  

Рис. 4.11

Итак, мы в состоянии изменить размерность, если слегка изменим правила порождения паттерна. Размерность изменяется вместе с правилами, но сама по себе она ровным счетом ни о чем не говорит.

Чтобы убедиться в этом, вернемся к фракталу, который изображен на рис. 4.10а. Ломаная кривая, в соответствии с вектором φ₁ = {0 0 1 2 0}, дважды проходит основание треугольника. Теперь заставим ее совершить еще один полный оборот по периметру треугольника, т.е. пусть она обовьет все стороны треугольника дважды, а его основание трижды. Такая процедура описывается следующим набором:

k = 2, n = 8, h = 3 и φ = {0 0 1 2 0 1 2 0}.

Несложно проверить, что при этих условиях фрактал не изменит своего внешнего облика, ломаная кривая будет проходить по тем же узловым точкам, что и в первом случае. Несмотря на то, что в новой ситуации рис. 4.10а нисколько не изменится, его прежняя размерность d = 2,32193 поменяется на новую, причем целочисленную — d = 3. В самом деле,

И что же, теперь наша ломаная перестала быть фракталом? Конечно же, нет. Поэтому не следует придерживаться того формального признака, будто фракталы имеют только исключительно дробную размерность. Очевидно, можно смоделировать и обратную ситуацию, когда два разных фрактала будут иметь абсолютно одинаковые размерности.

Таким образом, не столь уж и важно, какими первоначальными идеями руководствовались Кантор, Серпинский или Пеана, когда изобретали алгоритмы получения своих математических объектов. Точно так же, не имеет большого значения, о чем думал Хаусдорф, когда говорил о дробной размерности, или какую первоначальную задачу ставил перед собой Мандельброт, когда воспользовался его дробной размерностью при изложении своей книги. Сегодня актуальным является совершенно другое, а именно, реализация рекурсивного механизма роста фрактала на компьютере. Пусть термин «фрактал», изобретенный Мандельбротом, происходит от понятия дробной размерности, пусть эта идея привела в действие мощное интеллектуальное движение, однако при нынешнем состоянии дел понятие дробной размерности нельзя более считать чем-то основополагающим для вычерчивания тех симпатичных картинок, эстетика которых заставляет нас задуматься над их компьютерной реализацией. Ниже, при изучении динамических фракталов от функций ax(1 – x), axcos(x) и axexp(x), мы убедимся, что фрактал может состоять из бесконечного количества частей, испытавших на себе самые различные масштабные изменения.

Для понимания природы размерности фракталов типа губки Менгера или ее плоского аналога, ковра Серпинского, более продуктивным понятием, чем размерность, является мера внутренней емкости губки, которую условно обозначим через m. Если речь идет о плоском варианте, который изображен на рис. 4.7, то площадь самого тела губки (темные области) можно было бы измерять числом единиц m₁, а площадь ее пустого пространства (светлые треугольники) — числом нулей m₀. Если очередной шаг итерации обозначить через m, общее число символов в треугольнике со стороной катета в n единиц обозначить через N, то справедливы следующие простые выражения:

N = n (n + 1)/2, n = 2^{m + 1},

N = m₀ + m₁, m₁(m) = 3m₁(m – 1), μ_Δ = m₀/m₁.

По табл. 4.2 можно проследить, как увеличивается внутренний объем плоско-треугольной губки с увеличением числа итераций: через семь шагов относительный объем пустого пространства внутри губки, вначале составлявший 11%, через семь шагов достиг 400%, т.е. объем пустого пространства внутри губки стал в 4 раза больше объема самого тела губки

Таблица 4.2

m	n	N	m0	m1	μΔ
1	4	10	1	9	0,1111
2	8	35	9	27	0,3333
3	16	136	55	81	0,6790
4	32	528	285	243	1,1728
5	64	2078	1350	729	1,8518
6	128	8256	6069	2187	2,7750
7	256	32896	26335	6561	4,0139
...	...	...	...	...	...

Еще проще подсчитать число m для трехмерной губки Менгера кубической формы. Первый куб объемом 27 единиц содержит 7 единиц пустоты. Следовательно, для него μ_M = 7/20 = 0,35. Для второй губки, которая изображена на рис. 4.6 (а) и (б), общий объем равен 9³ = 729, из них 329 единиц составляет пустоту, отсюда μ_M = 329/400 = 0,8225. Эта тенденция сохраняется и в последующем: чтобы найти знаменатель m₁, нужно предыдущее число умножить на 20, т.е.

m₁(m) = 20·m₁(m – 1),  N = n³, m₀ = N – m₁, μ_M = m₀/m₁ = (N – m₁)/m₁.

Результаты расчета по этим формулам μ_M занесены в табл. 4.3, из которой видно, что темп роста внутренних полостей губки Менгера несколько выше, чем у плоско-треугольной губки Серпинского, рассмотренной перед этим.

Рис. 4.12

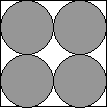
Теперь смоделируем губку, плоский вариант которой изображен на рис. 4.12. В квадрат площадью a² = 1 вписаны 4 круга с общей площадью π/4; темные круги — тело губки, т.е. величина m₁, а разность между площадью квадрата и площадью четырех кругов образует внутреннюю полость губки, т.е. величину m₀. Отсюда относительный объем пустого пространства для этой двухмерной губки равен

μº = m₀/m₁ = (1 – π/4)/(π/4) = 0,2732.

В трехмерном пространстве эта губка будет состоять из 8 шаров, плотно упакованных в куб объемом a³ = 1. Используя формулу для объема шара, подсчитаем величину μº для этого случая:

μº = (1 - m₁)/m₁ = 0,9098

В четырехмерном пространстве губка содержит уже 16 шаров, плотно упакованных в куб объемом a⁴ = 1. Общая формула для расчета объема шара, находящегося в многомерном пространстве, выглядит следующим образом: V_n = k_nrⁿ,где r — радиус шара (у нас он равен 1/4), Г(x) — гамма-функция, для которой справедливы следующие соотношения: Г(1) = 1, Г(1 + n) = n!, а также

Г(x) = (x – 1)Г(x – 1) = (x – 1)(x – 2)Г(x – 2) = ...,

Коэффициент k_n определяется формулой:

.

Для n = 2 коэффициент k₂ = π, так как Г²(1/2) = π, Г(2) = 1.

Для n = 3 коэффициент k₃ = 4π/3 = 4,1889, так как

Г³(1/2) = 5,5683; Г(1 + 3/2) = 1,5 × Г(3/2) = 1,3293;

k₃ = 5,5683/1,3293 = 4,1889.

Теперь найдем k₄, m₁ и μº для губки, находящейся в четырехмерном пространстве: 

Г⁴(1/2) = 9,8696;  Г(1 + 2) = 2;  k₄ = 4,9348;  

m₁ = 16 × V₄ = k₄/16 = 0,3084;  μº = 2,2425. 

Аналогичным образом рассчитывается относительная емкость губки в пространстве пяти, шести и любого другого числа измерений. Результаты расчета k_n, m₁, m₀, μº, а также сравнения величин μ_Δ и μ_M занесены в табл. 4.3. В этой таблице n означает размерность пространства, в котором находится губка, N — число шаров, плотно упакованных в кубе, сторона которого в четыре раза превышает радиус шара.

Таблица 4.3

n	N	kn	m1	m0	μº	μM	μΔ
2	4	3,1416	0,7854	0,2146	0,2732	0,3500	0,1111
3	8	4,1889	0,5236	0,4764	0,9098	0,8225	0,3333
4	16	4,9348	0,3084	0,6916	2,2425	1,4604	0,6790
5	32	5,2639	0,1645	0,8355	5,0790	2,3215	1,1728
6	64	5,1677	0,1645	0,9193	11,3916	3,4840	1,8518
7	128	4,7249	0,0369	0,9631	26,1003	5,0534	2,7750
8	256	4,0587	0,0159	0,9841	61,8931	7,1721	4,0139
...	...	...	...	...	...	...	...

Количественный анализ показывает, что в двумерном случае, который изображен на рис. 4.12, четыре круга закрывают свыше 78% площади квадрата; в трехмерном пространстве объем четырех шаров и объем свободного пространства куба почти сравнялись; а в четырехмерном мире 16 шаров занимают уже в два с лишнем раза меньше пространства, чем остается пустого пространства в кубе. Таким образом, эффективность шаровой губки намного выше, чем двумерных или трехмерных ее аналогов. Однако размещение шаровой губки в пространствах с различным числом измерений ничем особенным не отличается от ряда губок, полученных путем прямого перемножения матриц плоской губки Серпинского или объемной губки Менгера. Во всех случаях получается, что с каждым следующим расширением исходного паттерна происходит перенос губки в новое пространство. Увеличение размерности результирующей матрицы при прямом перемножении как раз и свидетельствует об увеличении размерности пространства, в котором существует губка.

Итак, при росте губок фрактальная размерность плоской губки Серпинского (рис. 4.7 или 4.10г и д), обозначим ее как d_Δ, или объемной губки Менгера (рис. 4.6а), обозначим ее как d_М, остается величиной неизменной:

   

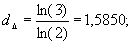
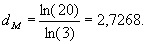
Но их геометрическая размерность увеличивается на единицу с каждым следующим расширением матрицы. Именно за счет расширения размерности пространства происходит добавление новых элементов фрактала. Но давайте подумаем вот над чем.

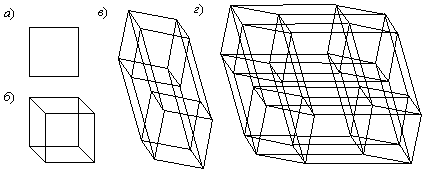
Рис. 4.13

На рис. 4.13 показана рекурсия куба в пространстве двух (а), трех (б), четырех (в) и пяти (г) измерений. Многомерные кубы образуют полноценный фрактал, хотя его рекурсия описывается не через прямое произведение матриц, а весьма простой геометрической процедурой проецирования. Шаровая губка, двумерный вариант которой изображен на рис. 4.12, является элементарным дополнением к фракталу, четыре шага которого изображены на рис. 4.13. В каждом из пространств число элементов куба — ребра, вершины и грани — будут увеличиваться, но различным образом. Число шаров или число вершин куба с увеличением размерности пространства на единицу удваивается, т.е. фрактальная размерность здесь, кажется, равна d = 2 и эта величина не изменяется. Но исходный паттерн (а) можно определить не через 4 вершины, а через 4 одинаковых и взаимно перпендикулярных ребра. Тогда переход к трехмерному пространству (б) дает не 8, а 12 ребер, т.е. d = 3. На следующем шаге их количество возрастет только до 32, а не 36 (в), как можно было бы ожидать, т.е. d = 32/12 = 2,667. Далее «фрактальная размерность» будет уменьшаться; так, для пятимерного пространства (г) число ребер становится равным 80, а d = 80/32 = 2,5 и т.д.

Таким образом, возникает неоднозначность: почему за исходный паттерн нужно брать четыре вершины квадрата или четыре вписанных в него окружностей, а, скажем, не четыре ребра или одну его грань? Этим вопросом мы хотим подчеркнуть, что определение «фрактальной размерности», как она дается в элементарных случаях, для объектов, геометрически устроенных более сложно, чем ломаная Коха, губка Серпинского или губка Менгера, вызывает неопределенность. В процессе рекурсии разные элементы сложно организованного паттерна не обязательно должны увеличиваться на одно и то же число, называемое « фрактальной размерностью».

И еще, если фрактал разворачивается по многомерным пространствам, означает ли это, что данным математическим структурам отвечает некая физическая реальность? Существуют ли на самом деле пространства четырех, пяти и большего числа измерений, где протекают фрактальные процессы? Ни в коем случае; будет большой ошибкой думать, что для тех или иных математических представлений в реальном мире обязательно найдется подходящий объект. Мы можем вообще отвлечься от понятия размерности пространства и прямого произведения матриц, и тогда вместе с ними исчезнет понятие о многомерном пространстве. Только догматически мыслящие люди могут настаивать, например, на том, что реально существует лишь псевдоевклидова геометрии, что кроме вероятностной интерпретации волновой функции других вариантов и быть не может, что модель сильной химической связи является единственно правильной. Это выглядит также абсурдно, как если бы кто-то считал десятичную систему счисления единственно верной, а двоичную — ложной. Те же самые фракталы, с еще большим успехом можно описать на языке порождающих грамматик или аффинных преобразований, где овсем иные представления о том, что может и что не может существовать в действительности. Конструктивный подход не исключает, а, наоборот, поощряет разномыслие в науке. Если кто-то думает иначе, пусть объявит аппарат порождающих грамматик лженаукой; ведь в его рамках не возникает понятий о дробной или целочисленной размерности.