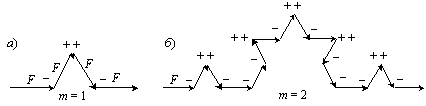Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

4.4. Грамматика на службе у фракталов

В рамках теории порождающих грамматик удобно организовать рекурсию, следовательно, аппарат формализованных языков можно использовать для разворачивания фракталов. В этом подразделе мы расскажем, как это лучше всего организовать, для чего вернемся к рис. 4.4, где изображена векторная диаграмма фрактала Коха. Припишем векторам другие символы, как показано на рис. 4.14. Данные символы образуют алфавит одного из вариантов формализованного языка Хомского, который позволяет по начальному слову с использованием некоторой совокупности правил подстановок, являющиеся обязательными атрибутами порождающей грамматики, генерировать все новые и новые слова, длина которых с каждым шагом будет возрастать. Диаграмму, вычерченную на рис. 4.14, называют татл-диаграммой. Английское слово turtle переводится как черепаха, а под черепахой понимается некий автомат для графической реализации так называемой L-системы. В 1968 г. ее ввел в обиход программистов Аристид Линденмайер, так что буква L одновременно является началом английского слова «язык» и началом фамилии разработчика.

Рис. 4.14

При изложении формального языка Линденмайера мы будем следовать Кроноверу, который, как он сам утверждает, заимствовал весь формализм L-системы из работы Прузинкевича и Ханана «Линденмайерские системы, фракталы и графики. Записи лекций по биоматематике» (1989). Прузинкевич и Ханан разработали изящные языковые правила для построения фрактальных диаграмм, которые напоминают в основном различные растения, хотя там есть рисунок снежинки и другие узоры. Мы полностью сохраняем введенные названными авторами обозначения. Три буквы, фигурирующие в татл-диаграмме фрактала Коха означают следующее: F — продвижение черепашки по ломанной Коха вперед на единицу длины, « + » — поворот черепашки на 60º по часовой стрелке и « – » — поворот черепашки на 60º против часовой стрелки.

Первая диаграмма (рис. 4.14а) задает единственное правило порождения новых слов, которое выглядит следующим образом: newf = F – F + + F – F. Всякая порождающая грамматика помимо алфавита и правил должна содержать начальное слово. В данном случае оно выглядит как axiom = F. Действуя на начальное слово axiom правилом подстановки newf, получаем первое слово S₁, которое повторяет правило: S₁ = F – F + + F – F. На втором шаге каждая буква F заменяется скобкой (F – F + + F – F). Так получается второе слово S₂, которое и отражается диаграммой, показанной на рис. 4.14б:

S₂ = (F – F + + F – F) – (F – F + + F – F) + + (F – F + + F – F) – (F – F + + F – F) = F – F + + F – F – F – F + + F – F + + F – F + + F – F – F – F + + F – F.

Грамматическое правило обеспечивает рекурсивную функцию, когда в качестве аргумента для нахождения очередного значения функции подставляется предыдущее значение функции, что обеспечивается простой подстановкой F = newf. Так, с помощью L-системы порождающей грамматики Линденмайера мы получаем фракталы.

Чтобы задать снежинку Коха вида, который показан на рис. 4.3 (а) и (б), нужно ввести соответствующее начальное слово:

axiom = F + + F + + F.

В этом случае первым словом будет следующее:

S₁ = (F – F + + F – F) + + (F – F + + F – F) + + (F – F + + F – F) = F – F + + F – F + + F – F + + F – F + + F – F + + F – F.

Если каждую букву F слова S₁ заменить скобкой (F – F + + F – F), мы получим второе слово S₂. Продолжая эту рекурсию, можно получить снежинку Коха S_m для любого числа шагов m. Начальное слово и правила для ломаной Пеано такие:

axiom = F, newf = F – F + F + F + F – F – F – F + F,

где прибавляется и отнимается угол 90°. Несложно составить самим грамматические правила для всех кривых, изображенных на рис. 4.5.

Для вычерчивания более сложных фракталов нам нужно расширить алфавит языка Линденмайера. Введем следующие новые буквы: b — переместиться на шаг вперед без прорисовки следа; [ — открыть ветвь; ] — закрыть ветвь. Алгоритм L-системы можно коротко описать следующим образом.

Вход:

axiom — начальное слово
newf — первое правило
newb — второе правило
l — число шагов
n — длина слова
T — массив

Выход: word — слово-результат

Инициализация:

W = axiom
T = { } — пустая строка

Шаги:         while l > 0

for j = 1 to n
if W(j) = +, T = {T +}, end if
if W (j) = –, T = {T –}, end if
if W (j) = [, T = {T [}, end if
if W (j) = ], T = {T ]}, end if
if W (j) = F, T = {T newf}, end if
if W (j) = b, T = {T newb}, end if, 
end for

W = T, l = l – 1

end while

word = W

В данном алгоритме переменная W (j) означает j-ую букву в слове word, {T +} — строка T, к которой добавлен знак +. При вычерчивании татл-диаграммы L-система действует по следующему алгоритму.

Вход:

word — результат работы предыдущего алгоритма
a — начальное направление
q — приращение по углу

Выход:

графическое представление word

Инициализация:

W = word 
x₀ = 0, y₀ = 0, n = length (word)
stack = { } — пустой стек

Шаги:

for j = 1 to n
if W (j) = +, a = a + q, end if
if W (j) = –, a = a – q, end if
if W (j) = – F, x = x₀ + cos a, y = y₀ + sin a
paint (x₀, y₀; x, y) — провести линию из точки (x₀, y₀) в точку (x, y)
x₀ = x, y₀ = y, end if
if W (j) = b, x = x₀ + cos a, y = y₀ + sin a, end if
if W (j) = [, l = length (stack),
stack (l + 1, 1) = x₀ ,
stack (l +1,2) = y₀ ,
stack (l +1,3) = a, end if
if W (j) = ], l = length (stack),
stack (l, 1) = x₀ , stack (l,2) = y₀ , stack (l,3) = a
del (l) — удалить l-ую запись из стека, end if
end for

В данном алгоритме при открытии ветви сохраняется значение координат и угла (x, y, a) в стеке, а затем система возвращается к этим значениям при закрытии ветви, при этом запись (x, y, a) из стека удаляется. Данные алгоритмы позволяют написать компьютерную программу на одном из языков программирования, которая способна будет вычерчивать диаграммы-узоры, приведенные на рис. 4.15.

а     б     в

г     д

е     ж

Рис. 4.15

Начальное слово и правила для рис. 4.15 будут такими:

а) Остров после двух итераций (q = p/2)

axiom = F + F + F + F, newf = F + F – F – FFF + F + F – F;

б) Цепочка Ян-Си Ло после трех итераций (q = p/2)

axiom = F + F + F + F, newf = F + b – F – FFF + F + b – F, newb = bbb;

в) Мозаика Патрика Хагерти после трех итераций (q = p/2)

axiom = F – F – F – F, newf = F – b + FF – F – FF – Fb – FF + b – FF + F + FF + Fb + FFF, newb = bbbbbb;

г) Сорняк после четырех итераций (q = p/7)

axiom = F, newf = F [ + F ] F [ – F ] F;

д) Куст после четырех итераций (q = p/8)

axiom = F, newf = – F + F + [ + F – F – ] – [ – F + F + F ];

е) Цветок Брандона Нельсона после трех итераций (q = p/2, a = p/2)

axiom = F [+ F + F ] [ – F – F ] [ + + F ] [ – – F ] F, newf = F F [+ + F ] [ + F ] [ F ] [ – F ] [ – – F ];

ж) Снежинка Джона Ву Кима после трех итераций (q = p/3)

axiom = [ F ] + [ F ] + [ F ] + [ F ] + [ F ] + [ F ], newf = F [+ + F ] [ – F F ] F F [ + F ] [ – F ] F F.