Конструктивная математика

Акимов О.Е.

31. Эффективная масса и поверхность Ферми

Вспомним, как вводился матричный элемент оператора импульса в форме

P_nm(k₀) = < u_nk0 | p | u_mk0 >.

Гамильтониан уравнения Шредингера H_k складывается из невозмущенной части H_k0 и возмущенной H'_k . Если величина возмущения мала (H'_k << H_k0), то закон дисперсии можно представить в виде

E_n(k) = E_n(k₀) + ћ²(k² – k₀²)/2m + ћ(k – k₀)P_nm(k₀)/m + 

+  .

Если точка k₀ экстремальная, то линейный член по P_nm(k₀) исчезает, и закон дисперсии будет определяться квадратом матричного элемента оператора импульса:

E_n(k) = E_n(k₀) + ,     (i, j = x, y, z),

где под m_ij понимается эффективная масса, определяемая выражением

= + .

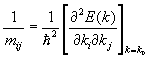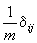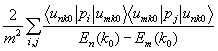Понятие тензора эффективной массы, о котором говорилось с самого начала, когда вводились первые понятия о законе дисперсии, широко используется, так как компоненты тензора можно измерить в эксперименте по циклотронному резонансу. Матрица эффективной массы поддается диагонализации, что позволяет найти три собственных значения m_x, m_y, m_z. Тогда закон дисперсии вблизи экстремума запишется как

E_n(k) – E_n(k₀) = + + .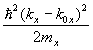

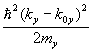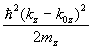Часто два из трех компонентов эффективной массы одинаковые, и тогда говорят о продольной и поперечной массе. Физический смысл эффективной массы состоит в том, что направление ускорения электрона ( dv/dt ) под действием кристаллического поля V(r) не совпадает с направлением силы ( F ). Если в изотропном пространстве движение электрона описывается уравнением

или ,

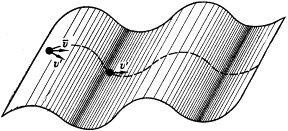
то в анизотропном пространстве кристалла масса зависит от направления движения (рис. 49):

.

Рис. 49

Физический смысл квадратичной зависимости закона дисперсии тоже понятен: в экстремальных точках энергетические уровни можно аппроксимировать параболами, вдали от этих точек линии уровней спрямляются и их можно аппроксимировать прямыми или, если речь идет о k-пространстве, плоскостями. При поиске параметров импульса возникает потребность опереться на какую-то, пусть грубую, модель всех энергетических уровней в целом. Эту модель не может дать зонная структура пустой решетки (рис. 44а), поскольку вблизи запрещенной зоны кристаллический потенциал слишком сильно искривляет общую картину энергетических состояний (см. рис. 44б). Значит, требуется более адекватная пространственная модель уровней, дающая наглядное представление о расположении энергетических зон. Такая модель может быть получена за счет линейной аппроксимации закона дисперсии, когда ее квадратичный компонент опускается, а линейный удерживается:

E_n(k) = E_n(k₀) + ћ(k – k₀)P_nm(k₀)/m.

Этот линейный закон описывает положение плоскостей в четырехмерном пространстве энергии и волнового вектора (E, k_x, k_y, k_z). В следующем пункте ставится задача получения числовых значений коэффициентов уравнений плоскости для уровней германия и кремния. Но прежде, чем мы приступим к решению этой линейной задачи, необходимо рассмотреть вопрос с противоположной стороны, а именно: как выглядят максимально искривленные поверхности вблизи точек экстремума.

Закон дисперсии E_n(k) — функция четырехмерного пространства; чтобы ее отобразить в трехмерном k-пространстве, требуется прибегнуть к небольшой хитрости. Первый способ состоит в том, чтобы выбрать определенное направление в k-пространстве и вдоль него вычертить значения энергии (этим способом мы до сих пор пользовались). Второй способ состоит в том, чтобы вычертить в трехмерном объеме k-пространства одну-единственную энергетическую поверхность постоянного значения. Возникает вопрос: какую поверхность постоянной энергии нужно вычертить, чтобы она наиболее полно характеризовала изучаемый материал? Здесь и появляется понятие о поверхности Ферми, которое потребует от нас некоторых разъяснений.

Число значений волнового вектора k внутри зоны Бриэллюэна (ЗБ) равно числу элементарных ячеек в кристалле, которое мы обозначим N. Так как в каждом состоянии могут находиться два электрона с противоположными спинами, то число разрешенных состояний, приходящихся на одну энергетическую зону, равно 2N. Если полное число электронов проводимости, отдаваемых всеми атомами, находящимися в каждой элементарной ячейке кристалла, равно n, то полное число электронов проводимости, которые нужно разместить в различных возможных состояниях, характеризуемых величинами k и E_i(k), равно nN. Значит, эти электроны заполнят nN/2N = n/2 зон в ЗБ. Какие именно из 2N состояний будут заняты электронами, определяется законом распределения Ферми — Дирака. Вероятность того, что состояние с волновым вектором k в зоне E_i(k) при температуре Т будет занято, определяется формулой:

,

где E_F — энергия Ферми и k_B — постоянная Больцмана. При Т = 0 зоны E_i(k) < E_F будут заняты электронами, а зоны E_i(k) > E_F окажутся свободными; при температуре Т > 0 часть электронов перейдет в зону проводимости (ЗП), которая для проводников, где нет запрещенной зоны (ЗЗ), находится сразу же выше уровня Ферми. Таким образом, энергия E_F играет ключевую роль, особенно для металлов; поверхность постоянной энергии, определяемая уравнением E_i(k) = E_F и называется поверхностью Ферми. Для полупроводников понятие энергия Ферми существенно девальвирует: для этого класса материалов более важными энергиями являются величины, соответствующие потолку и дну ЗЗ. Поскольку в ЗЗ располагаются энергетические уровни примесей, то для сравнения этих уровней иногда оказывается полезно ориентироваться на Фреми-уровень, как некий порог, с которого начинается движение акцепторов и доноров в полупроводнике.

Ферми-поверхность может представлять собой сфероид, эллипсоид, односвязанную или многосвязанную поверхность. Причем эти поверхности не обязательно должны быть целиком замкнуты в первой ЗБ, поскольку они могут иметь продолжение в соседние ЗБ. Физические свойства материалов в значительной степени зависят от топологии поверхности Ферми. В общем виде кривизна зоны E_i(k) записывается

,

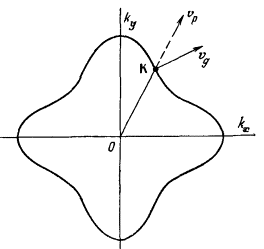
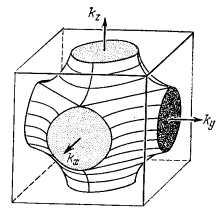
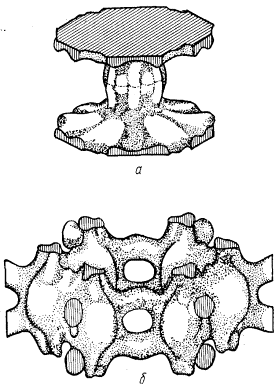
где m_ср — средняя эффективная масса, v(k) — скорость электрона, α — угол между направлениями групповой (v_g) и фазовой (v_p) скорости для деформированных изоэнергетических поверхностей (рис. 50). Более точное аналитическое выражение, связывающее эффективную массу с кривизной поверхности Ферми, выглядит более сложно.

Рис. 50

Расчетная топология изоэнергетических поверхностей вообще и поверхность Ферми в частности существенно зависит от метода приближения, по которому ведется расчет. Предположим, что электрон в основном s-состоянии (для p, d и других состойний формулы будут сложнее) движется в поле V(r) изолированного атома. Тогда, как было сказано выше, волновая функция одного электрона в кристалле ψ_k(r) может быть записана в виде линейной комбинации атомных функций φ(r – r_j):

.

Функция ψ_k(r) является блоховской, а это значит, что коэффициенты в линейной комбинации имеют вид 

C_ki = N^–½ exp(ik · r_j). 

Отсюда проистекает, что

.

Энергия ищется как диагональный матричный элемент гамильтониана H:

;

здесь φ_m = φ(r – r_m). Если ввести вектор ρ_m = r_m – r_j, то

.

В приближении сильной связи всеми интегралами перекрытия атомных функций можно пренебречь, за исключением двух, относящихся к интегралу перекрытия собственных функций атома и интегралу перекрытия функций данного атома с функциями ближайшего соседа, отстоящего на расстоянии ρ, т.е.

     и     .

Знак минус говорит, что за счет сближения атомов, потенциальный барьер для туннелированния электрона от одного атома к другому снижается.

Таким образом, для энергии в первом приближении сильной связи имеем следующее выражение:

.

В ПК решетке с периодом а каждый атом окружен шестью соседями (±a, 0, 0), (0, ±a, 0), (0, 0, ±a). Если оси координат x, y, z направлены по ребрам куба, то сумма распишется как

= exp(ik_xa) + exp(–ik_xa) +

+ exp(ik_ya) + exp(–ik_ya) + exp(ik_za) + exp(–ik_za).

После преобразования суммы, закон дисперсии для ПК решетки приобретет вид

E(k) = –A – 2B(cosk_xa + cosk_ya + cosk_za).

В ОЦК решетке число ближайших атомов равно 8 и закон дисперсии выглядит иначе

E(k) = –A – 8B(cosk_xa/2)cos(k_ya/2)cos(k_za/2).

В ГЦК решетке число ближайших атомов равно 12 и закон дисперсии имеет вид

E(k) = –A – 4B[cos(k_xa/2)cos(k_za/2) +

+ cos(k_ya/2)cos(k_xa/2) + cos(k_za/2)cos(k_ya/2)].

Для ПК решетки при условии k_x = k_y = k_z = 0, 

E_min = –A – 6B;

при k_x = k_y = k_z = π/a, энергия будет максимальной:

E_max = –A + 6B.

Следовательно, ширина разрешенной энергетической зоны равна 

ΔE = E_max – E_min = 12B.

Аналогичные рассуждения, проведенные для ОЦК решетки, дают

ΔE = E_max – E_min = 8B – (– 8B) = 16B;

и такое же значение для ГЦК:

ΔE = E_max – E_min = 4B – (– 12B) = 16B.

При ka << 1 для ПК решетки из разложения косинусов получаем

E(k) ≈ –A – 6B + Bk²a².

Вблизи дна ЗП энергия не зависит от направления движения и эффективная масса электрона будет равны

m = ћ²/2Ba². 

Отсюда видно, что при большом значении интеграла перекрытия соседних атомов (т.е. параметра B) разрешенная зона энергии для электрона (т.е. параметр ΔE) увеличивается, но его эффективная масса уменьшается и наоборот.

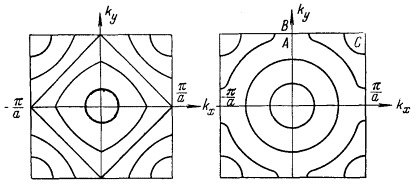
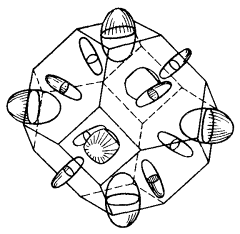
На рис. 51а приведены изоэнергетические уровни, рассчитанные по упрощенной методике, которая была продемонстрирована только что. Здесь энергии E = – A + 2B соответствуют прямые типа k_x + k_y = π/a, соединяющие середины ЗБ ПК решетка. На рис. 51б приведены изоэнергетические уровни, полученные в приближении слабой связи. Их сравнение показывает, что в центре и вблизи вершин квадрата ЗБ энергетические уровни схожи, но на осях k_x и k_y, а также в средней части ЗБ ПК решетки уровни сильно отличаются. 

Рис. 51

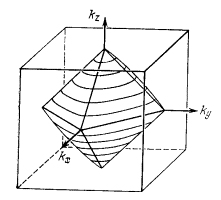
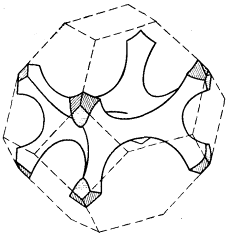
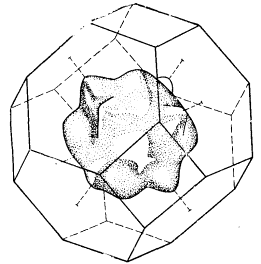
На рис. 52а показан изоэнергетический октаэдр ЗБ ПК решетки, отвечающий всё той же энергии E = –A + 2B; при другом значении энергии, а именно, при E = –A, поверхность становится криволинейной (рис. 52б). Внутренний объем обеих фигур, показанных на рис. 52а и 52б, заключают в себе электронные состояния. На рис. 52в показано дополнение к поверхности, которая изображена на рис. 52б; внутренний объем этой фигуры отделяет уже дырочные состояния.

а)

б)

в) .

Рис. 52

Изоэнергетические линии и поверхности, изображенные на рис. 51 и рис. 52, носят грубо-теоретический, качественный характер. В реальных полупроводниках дело обстоит намного сложнее. Впрочем, вблизи точки k = 0 всё-таки допустимо пользоваться приближенной формулой для закона дисперсии в виде

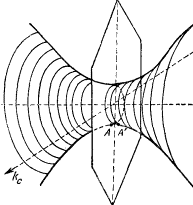
E(k) = Ak² ± [B²k⁴ + C²(k_x²k_y² + k_y²k_z² + k_z²k_x²)]^½,

где A, B, C — экспериментальные параметры конкретных полупроводников. Два знака перед корнем дают две поверхности: минус для тяжелых дырок, плюс для легких.

Для Ge и Si имеют место следующие значения эффективной массы: m_l /m — продольная масса электронов; m_t/m — поперечная масса электронов; m_h1/m — эффективная масса тяжелых дырок; m_h2/m — эффективная масса легких дырок; m_h3/m — эффективная масса дырок отщепленной зоны. В табл. 40 приведены параметры в единицах ћ²/2m и эффективные массы в единицах массы свободного электрона m.

Таблица 40

	–A	| B |	| C |	ml /m	mt/m	mh1/m	mh2/m	mh3/m
Ge	13.3	8.6	12.5	1.64	0.082	0.28	0.044	0.077
Si	4.0	1.1	4.1	0.98	0.19	0.49	0.16	0.245

Три дырочных массы определяются трехкратно вырожденным состоянием Г '₂₅ валентной зоны. От него отходят две относительно крутые долины Δ'₂ и Λ₁ (рис. 47) с малой кривизной вблизи точки k = 0, определяющие массу тяжелых дырок m_h1. От Г '₂₅ отходят также две пологие двукратно вырожденные долины Δ₅ и Λ₃, которые определяют массу легких дырок. В результате спин-орбитального взаимодействия двукратное вырождение слегка снимается, почему и возникают две разновидности легких дырок m_h2 и m_h3. Параметры закона дисперсии вблизи точки k = 0 связаны формулами:

, , .

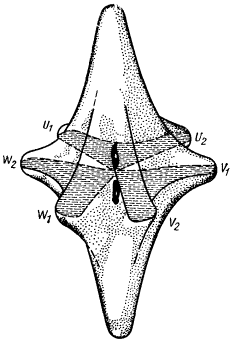
Минимум зоны проводимости у кремния находится в Δ-направлении ЗБ, т.е. на осях k_x, k_y, k_z. Отношение между продольной и поперечной массами электронов, равное m_l/m_t = 5, определит степень вытянутости шести эллипсоидов постоянной энергии (рис. 53). Минимум зоны проводимости у германия находится в Λ-направлении около точки L, а это означает, что изоэнергетическая поверхность вблизи минимума у него представляется восемью половинками эллипсоидов, обрезанных гексагональной гранью первой ЗБ. Отношение малой оси эллипсоида к большой равно 1 : 2.

.

Рис. 53

В табл. 41 по материалам [47], [56], [57] приведены параметры A, B, C, эффективные массы электронов m_e, тяжелых m_hh и легких m_lh дырок. C увеличением ширины ЗЗ E_g (измеряется в эВ) эффективная масса электронов и легких дырок растет. 

Таблица 41

	–A	| B |	| C |	me /m	mhh/m	mlh/m	Eg
InSb	26.5	24.1	13.9	0.015	0.4	0.016	0.23
InAs	17.1	14.9	10.9	0.024	0.41	0.026	0.36
GaSb	11.2	7.9	10.2	0.042	—	0.052	0.81
GaAs	7.39	4.93	5.06	0.065	0.68	0.07	1.52
GaP	4.72	2.52	2.70	0.135	—	—	2.3
InP	8.13	5.81	5.11	0.078	—	—	1.42
AlSb	5/51	2.84	3.65	0.121	—	—	1.6

Далее приводятся рисунки ферми-поверхности для реальных металлов, взятые из работы [58].

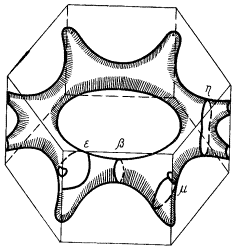
Топология поверхности Ферми для меди, серебра и золота приблизительно одинаковая и представляет собой гофрированный сфероид, который через узкие трубки соединяется со сфероидами соседних ЗБ. На рис. 54а показан сфероид меди; на рис. 54б изображено соединение двух сфероидов в плоскости гексагональной грани, а на рис. 54в дана общая картина соединения нескольких ферми-сфероидов.

а)

б)

в) .

Рис. 54

На рис. 55 показана многосвязанная ферми-поверхность дырочного типа для кальция (а), магния (б) и цинка (в)

а)

б)

в) .

Рис. 55

Электронная поверхность Ферми для родия и палладия схожи (рис. 56а), но их дырочные ферми-поверхности различаются: для родия она показана на рис. 56б, для палладия — на рис. 56в.

а)

б)

в) .

Рис. 56

На рис. 57а показана электронная поверхность Ферми кадмия. Энергия Ферми в хроме, молибдене и вольфраме отвечает нескольким замкнутым электронным и дырочным поверхностям (рис. 57б). На рис. 57в изображена многосвязанная электронная поверхность Ферми β-латуни (CuZn), имеющая дырочные «карманы».

а)

б)

в) .

Рис. 57

На рис. 58а представлена сложная многосвязанная ферми-поверхность скандия (электронная область заштрихована). На двух следующих рисунках приведены поверхности лантаноидов: б) тербия (вверху дырочная область, внизу электронная) и в) тулий (дырочная область заштрихована).

а)

б)

в) .