Конструктивная математика
Акимов О.Е.
32. Линейная аппроксимация закона дисперсии
Чтобы более наглядно продемонстрировать роль линейных элементов зонной структуры, обратимся к восьми нижним состояниям зоны проводимости германия на гексагональной грани ЗБ (рис. 59). Расчет данной зоны производился с помощью гамильтониана Г(15 × 15) с параметрами Ge(10), взятыми из табл. 32.
а) 
б) 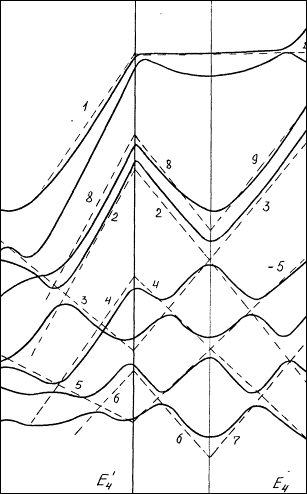
Рис. 59
Пунктирными прямыми обозначены следы от энергетических плоскостей, которые снабжены цифрами. На рис. 59а показаны четыре сечения Е1, Е2, Е4 и Е5. Два связанных сечения Е2 и E'2, показанные на рис. 59б, даны для того, чтобы можно было проследить связь энергетических уровней на гексагональной грани ЗБ с уровнями, расположенными ближе к центру ЗБ. Сечение E'2 проведено параллельно оси kz.
Центральное сечение E3 изображено на следующем рис. 60а вместе с внутренними сечениями E'3, E''3, E'''3, параллельными линии E3 и проведенными в глубине ЗБ. Общего числа сечений, представленных на рис. 59 и 60 достаточно, чтобы восстановить линейную конфигурацию восьми нижних состояний зоны проводимости германия. На рис. 60б показано пространственное расположение первых трех из восьми плоскостей.
а) 
б)  .
.
Рис. 60
Из сравнения сечений Е1 – E5 видно, что энергетическое состояние, соответствующее пунктирной прямой 1, опускается с уровня приблизительно 1,7 Ry (Е1) до уровня 0,4 Ry (Е5). Причем изменение величины энергии происходит пропорционально движению плоскости сечения Е по гексагональной грани ЗБ. Таким образом, состояние 1 скользит вдоль наклонной плоскости, которую мы будем также обозначать цифрой 1 (рис. 60б). Теперь обратимся к состояниям 2 и 3. Угол пересечения этих состояний на всех сечениях Е1 – E5 остается неизменным. Точка пересечения состояний смещается, начиная приблизительно с уровня 0,75 Ry (Е1) до уровня 1,35 Ry (Е5). Следовательно, можно говорить о наличии еще двух наклонных и пересекающихся плоскостей.
В центральном сечении Е3 все три прямые 1, 2, 3 пересекаются в одной точке с энергией 0,93 Ry. Наклон плоскостей одинаковый, а вся фигура, образованная этими плоскостями в шестиугольной призме, основанием которой является гексагональная грань, имеет ось симметрии третьего порядка C3. Аналогичные фигуры из трех пересекающихся плоскостей можно построить на плоскостях, параллельных гексагональной грани, но лежащих в глубине первой ЗБ. Из сравнения сечений E3, E'3, E''3, E'''3 видно, что энергия пропорционально уменьшается по мере приближения сечения E3 к точке Г. Следовательно, от сечения E3 к сечению E'''3 необходимо производить простую коррекцию уравнений путем умножения всех параметров на один и тот же коэффициент.
Величина отклонения энергетического состояния от идеальной плоскости по мере приближения его к центру ЗБ хорошо прослеживается на двух связанных сечениях E2 и E'2: чем ближе к центру ЗБ, тем с меньшим правом мы можем пользоваться линейной аппроксимацией. На рис. 60а видно, что двукратно вырожденному состоянию Lu3 отвечает точка пересечения плоскостей 2 и 3, а одномерное состояние Lu1 связано с плоскостью 1. Таким образом, модельные плоскости без привлечения теории групп объясняют природу двумерных состояний типа L3, Λ3, Δ5. Более того, тщательный анализ пространственной конфигурации плоскостей делает понятными правила отбора и соотношения совместности представлений. Все эти алгебраические приемы, по существу, классифицируют плоскости по их геометрическим свойствам.
Следующий шаг состоит в том, чтобы записать уравнения плоскостей в удобной системе координат. Первая система координат вводится на гексагональной грани ЗБ с осями Е, k'x, k'y. По формулам аналитической геометрии записывается в трехмерном пространстве. Однако сечения E'3, E''3, E'''3 дают глубину ЗБ и, тем самым, вводят еще одно измерение. Три плоскости, обозначенные 1, 2 и 3, по выбранным соответствующим образом точкам можно записать в пространстве четырех измерений Е, kx, ky, kz. Но при наличии оси симметрии третьего порядка, как и следовало ожидать, три уравнения плоскости переходят одно в другое при циклической перестановке координат волнового вектора kx, ky, kz, так что требуется выразить через уравнение лишь одну плоскость:
0,270 kx – 0,704 ky + 0,432 kz – 0,495 E + 0,477 = 0.
Данное уравнение и есть конкретное выражение линейного закона дисперсии En(k) для целой группы состояний, объединенных системой трех плоскостей.
Все рассуждения, относящиеся к плоскостям 1, 2, 3, можно перенести на нижние плоскости, которые обозначены цифрами 4, 5, 6, 7, 4', 5'. Уравнение плоскости 6 можно получить из уравнения плоскости 7, поменяв местами переменные ky и kz, а координату kx оставив без изменения. Осуществив таким образом перестановку координат, из этих двух уравнений получаем еще четыре. Приведем одно из них:
0,164 kx – 0,609 ky + 0,532 kz – 0,452 E + 0,053 = 0.
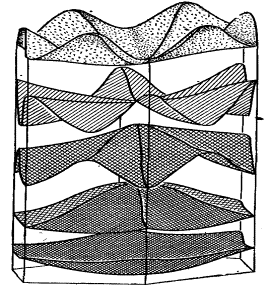
Шесть плоскостей, аппроксимирующих все нижние состояния зоны проводимости, нетрудно вычертить отдельно, как мы это уже делали для плоскостей 1, 2, 3 (рис. 60б). Однако лучшей иллюстрацией взаимного расположения этих плоскостей является графическое изображение точного машинного расчета дна зоны проводимости германия, показанного на рис. 61а. Симметрия этой поверхности для других тетраэдрических полупроводников такая же.
а) 
б) 
Рис. 61
Сложную топологию энергетических поверхностей количественно лучше всего характеризовать с помощью изоэнергетических линий. Геодезия этих линий дна зоны проводимости германия приведена на рис. 61б. Числами на линиях обозначены уровни энергии в ридбергах, отсчитанные от потолка валентной зоны ( Г '25). В центре розетки находится минимум зоны проводимости Ge. Глубина складок энергетической поверхности потолка валентной зоны меньше, чем у поверхности дна зоны проводимости (рис. 62а), однако влияние линейных элементов закона дисперсии можно проследить и здесь. Общая структура энергетических зон в гексагональной плоскости первой ЗБ для полупроводников IV группы изображена на рис. 62б.
а)
б)Рис. 62
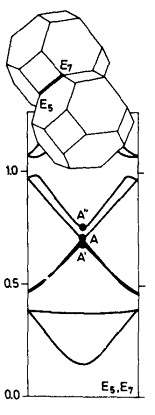
Зонные структуры на двух противоположных ребрах Е1 и E5 (рис. 59а) сильно различаются. Между тем все ребра первой ЗБ находятся в абсолютно одинаковом положении и, следовательно, должны иметь абсолютно идентичные зонные структуры. Несовпадение энергетических уровней говорит о неточности нахождения матричных элементов импульса или о недостаточном числе узлов, по которым составлялся исходный гамильтониан. В частности, все графики, представленные на рис. 59 – 62, рассчитывались гамильтонианом Г(15 × 15). Если использовать гамильтониан Г(27 × 27), то расхождений в структуре зон на ребрах Е1 и E5 ЗБ будет меньше. Но лучшее совпадение уровней энергии демонстрирует график, изображенный на рис. 63, который рассчитывался с помощью гамильтониана Г(200 × 200) с матричными элементами потенциала. Не обсуждая сейчас величину и причины расхождения в точках А, А' и А'', можно уверенно сказать, что они являются прекрасным ориентиром в подгонке матричных элементов гамильтониана.
Рис. 63
Строгая периодичность уровней во многом нарушается на ребрах ЗБ, однако непрерывность плоскостей в обратном пространстве кристалла сохраняется. Остаются неизменными и основные принципы для составления уравнений. Записав единственное уравнение относительно какого-либо узла решетки, моно получить все другие уравнения путем переноса начала системы координат последовательно во все узлы решетки.
Аппроксимация сложного энергетического ландшафта формами, индуцированными только линейными элементами закона дисперсии, дает в руки теоретиков инструмент для оценки фактических данных и увязывания их с зонной теорией в целом. Несомненно, параметры импульса в линейных уравнениях плоскости можно связать с конкретными электрофизическими и оптическими характеристиками полупроводников. И, уж во всяком случае, они являются хорошими идентификаторами химических элементов. Например, аналогичные уравнения для кремния выглядят иначе, чем для германия:
0,106 kx – 0,590 ky + 0,480 kz – 0,638 E + 0,320 = 0,
0,330 kx – 0,723 ky + 0,394 kz – 0,490 E + 0,433 = 0.
Одним из важных результатов этого анализа является то, что с помощью линейного закона дисперсии можно предсказать расположение многих энергетических уровней, первоначально не включенных в гамильтониан Г(15 × 15). Если, помимо циклических перестановок, типа kx → ky, ky → kz, kz → kx, в линейных уравнениях осуществить преобразование, типа kx → kx, kz → ky, kz → ky, то мы получим еще три недостающих линейных уравнения, существование которых продиктовано узлом {220}, не вошедшим в гамильтониан Г(15 × 15). Чтобы определить их пространственное расположение, достаточно совместить сечение Е1 с E5, а также Е2 с E4 (рис. 59а). Тогда уровни 4 и 5, совпадут с уровнями 4' и 5', а уровни 1, 2, 3 сечения Е1 (E2) перейдут на диаграмму уровней сечения Е5 (E4) уже как 1', 2', 3', и наоборот (уровни 6 и 7 являются общими для всех сечений).
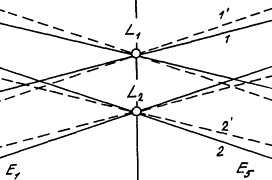
Кроме того, пространственное расположение плоскостей позволяет понять эффект шарнира, который приводит к неоднозначности нахождения матричных элементов импульса (табл. 32, Ge(10) — Ge(5)). Суть его поясняется рис. 64. Меняя величину импульса, в том числе и при их подгонке, энергетический зазор между двумя экспериментальными точками L1 и L2, лежащими на симметричном направлении, может оставаться постоянным, а общий ход энергетических уровней на периферии ЗБ, например на ее ребрах, будет сильно различаться (расположение уровней 1 и 2 отличается от 1' и 2' ). Отсюда становится понятно, что нельзя при поиске параметров ориентироваться только на симметричные точки и направления ЗБ.
Рис. 64
Три плоскости (рис. 60б) находятся как бы на шарнире; точка пересечения трех плоскостей с энергией Lu3 (Lu1), известная из эксперимента, не позволяет однозначно определить величину импульса, если его не искать с учетом уравнений плоскостей (сечения Е1 и E5, Е2 и E4 на рис. 59а) и совпадающих (вырожденных) значений на ребрах ЗБ типа точки A, которая на рис. 63 в виду погрешности расщепилась на две дополнительных точки — А' и А''.
Таким образом, чтобы исключить эффект шарнира, а, следовательно, неоднозначность матричных элементов импульса, необходимо при подгонке параметров иметь в виду всю энергетическую зону в целом. В компьютерной программе поиска параметров нужно непременно предусмотреть условия выполнения уравнений аппроксимирующих плоскостей. Без этих вспомогательных средств невозможно правильно отыскать параметры импульса для гамильтониана Г(27 × 27).