Приложение III. Вихревая теория материи

З. Цейтлин

ВИХРЕВАЯ ТЕОРИЯ МАТЕРИИ, ЕЕ РАЗВИТИЕ И ЗНАЧЕНИЕ

— 1 —

Предпосылки вихревой теории материи мы находим в учениях древнегреческих философов — Анаксимандра, Гераклита, Парменида, Зенона и Аристотеля. Но основоположником этой теории необходимо считать Маркса физики — Ренэ Декарта, который впервые вполне отчетливо и глубоко формулировал смысл и значение учения о вихревой природе материи. Принципы вихревой физики изложены Декартом в трактате , "О мире" (Du Monde), "Принципах философии", "Возражениях и ответах" (Objections et Reponses), переписке философа. Но так как философия Декарта, по справедливому замечанию А. Рея, это—-его физика, то все основные труда Декарта являются фундаментом этой физики. К несчастью, сам философ, и, само собой разумеется, его последователи так запутали картезианскую философию, т. е. физику, что она понимается обычно совершенно ложно.

Это ложное понимание принципов физики Декарта можно обозначить как псевдокартезианство или абсолютный рационализм. Сущность псевдокартезианизма в том, что он не принимает во внимание философских оснований картезианской физики, т. е. метода Декарта. Отсюда и произошла знаменитая борьба между относительно формальной физикой Ньютона и крайним рационализмом псевдокартезианцев, при чем относительный формализм Ньютона превратился у его последователей в абсолютный, который и противопоставлялся абсолютному рационализму. Эта историческая борьба тянется до сих пор и очень плодотворна по своим результатам, так как она постепенно выявляет истинный метод науки. Этапы борьбы заключаются в постоянной смене эпох абсолютного рационализма и абсолютного формализма, согласно общеизвестному закону диалектического движения. Период от появления идей Декарта до 1740 года был периодом господства псевдокартезианизма.

Философы и физики стремились объяснить все физические явления при помощи однородной непрерывной материи (пространства как физического тела), находящейся в непрерывном движении, подчиненному закону сохранения.

Везде физика излагалась по картезианскому учебнику Rоhault (*). Замечательно то, что в течение 30 лет после появления "Начал" Ньютона эти "Начала" не сумели вытеснить книги Рого. Ревностный приверженец Ньютона Самуил Кларк выпустил в течение 13 лет (1697 — 1710) три латинских издания этого учебника, при чем издатель только в примечаниях решился изложить принципы Ньютона, не упоминая, однако, в первых двух изданиях его имени.

(*) Жак Рого (Jacques Rоhault, 1618 – 1672), сын богатого торговца вином, получил традиционное схоластическое образование в Париже, но вскоре принял и популяризировал физику Декарта. С 1650 он начал читать лекции по "механической" философии Декарта, согласно которой "маленькие фигурные тела" являются основой физической реальности. В 1671 году он издал "Физический трактат" ("Traité de physique"), который стал первым "стандартным" учебником по физике. Помимо изложения основных положений Декарта, Трактат включал также элементы учений известных картезианцев: Блеза Паскаля, Христиана Гюйгенса и т.д.

"Английский перевод появился в 1735 году: Rohault Jacques. System of Naturad Philosophy illustrated with D-r Samuel Clarkes notes taken from Sir Isaac Newton. Латинский экземпляр имеется в библиотеке Московского университета".

Это сообщил Цейтлин в сноске, но на сей счет появилась другая информация в Интернете. Трактат Рого переведен на английский язык в 1723 году известным учеником Ньютона Samuel Clarke (1675 – 1729) и его братом, которые внесли в исходный текст учебника множество исправлений и дополнений. Этот текст идет под названием "Samuel Clarke’s Annotations in Jacques Rohault’s Traité de Physique, and How They Contributed to Popularising Newton’s Physics".

Вместе с Трактатом Жака Рого в Европе получило широкое хождение другой учебник по естественной философии (Fundamenta physices), написанный голландским философом и врачом Хендриком де Руа или де Ройя (Hendrik De Roy), голландцы зовут его Хендрик ван Рой (Henrik van Roy), французы — Анри Ле Рой (Henri Le Roy), латинизированное имя — Энрикус Реджус (Henricus Regius).

Он жил в период с 1598 по 1679 год, преподавал в старейшем (основан в 1636 году) университете города Утрехта, где и умер. В молодые годы он побывал в Париже и Монпелье; где-то там его ограбили, после чего он записался во французскую армию; затем учился в Университете Падуи; 29 марта 1623 года получил степень доктора медицины; он — неистовый поклонник теории кровообращения английского врача Уильяма Гарвея (William Harvey, 1578 – 1657), которым восхищались картезианцы.

Де Рой переписывался с Декартом, спорил и не соглашался, но никогда не встречался с ним, в частности, он отверг идею Декарта о врожденных идеях. Разошлись они и в вопросах религии: Декарт номинально считался католиком, которого профессор теологии и первосвященник Утрехта Гилберт Войт (Gilbert Voet или Voetius) подозревал в атеизме, а Де Рой — фанатичным кальвинистом, протестантом на французский манер). Вскоре после публикации "Философии природы" Анри ле Руа (так назовем автора), который вышел в 1646 году, а после еще два раза — в 1654 и 1661, между ними произошел окончательный разрыв.

Сегодня в Интернете можно найти переписку Анри ле Руа (= Хендрик де Ройя = Henricus Regius) с Декартом (Descartes) на английском языке: "The Correspondence between Descartes and Henricus Regius. De briefwisseling tussen Descartes en Henricus Regius (met een samenvatting in het Nederlands)", а также саму "Философию природы" — труд во всех отношениях замечательный. Приведем титул, портрет и три десятка страниц с картинками из этого почти 600 страничного сочинения. Пусть этот материал не слишком отвечает заголовку данного раздела, тем не менее, картинки лучше слов рассказывают нам, о чем эта книга. Мы ясно увидим, что математические спекуляции Ньютона сильно проигрывают по сравнению с реальной физикой, которую начали разрабатывать картезианцы.

Де Рой привел довольно много рисунков из сочинения Декарта (мы тоже для примера взяли 3-4 из них). Однако по сравнению с французом голландец намного больше уделяет внимание физическим экспериментам, астрономическим наблюдениям, включая наблюдения солнечных пятен, Луны и ее затмения. Как профессиональный врач, автор пишет об анатомии и физиологии живых организмов; не забыл он и о насекомых. Даже по приведенным только здесь картинкам, мы видим, что его учебник охватывает практически все наиболее важные достижения науки XVII века.

Итак, посмотрите нашу подборку, которая начинается, однако, с портрета Жака Рого, упомянутого Цейтлином. Добавим также, что всем картинкам присвоен номер, соответствующий номеру страницы "Философии природы", откуда картинка взята. Сразу после картинок продолжим цитировать основной текст, посвященный вихрям. — О.А.

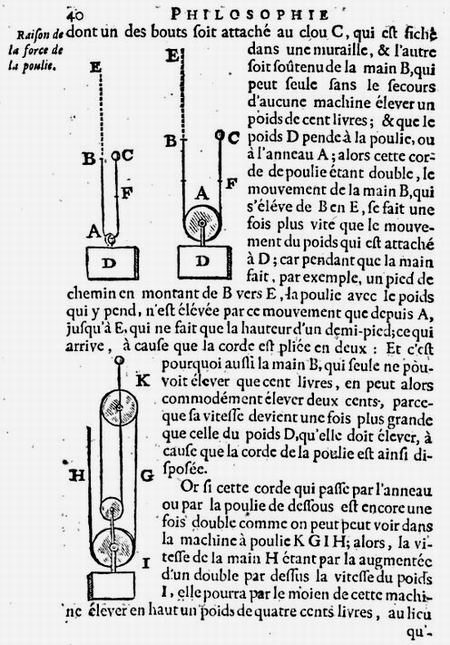
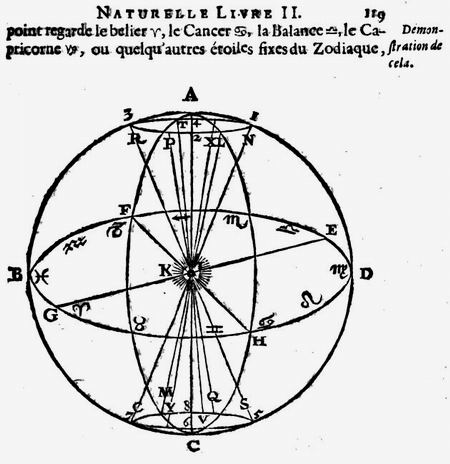
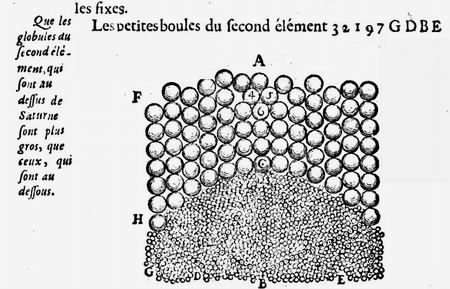
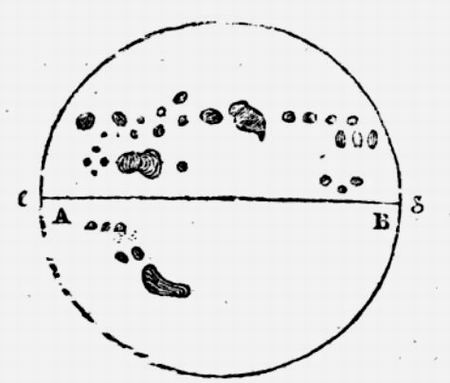
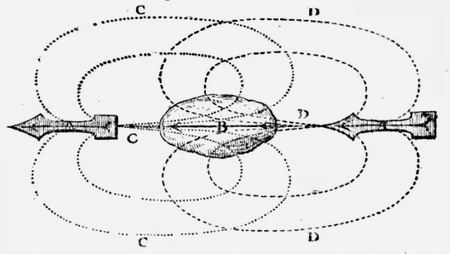
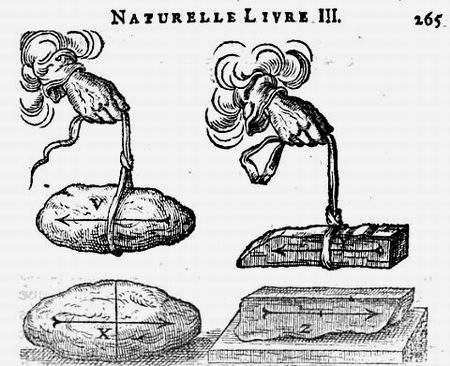
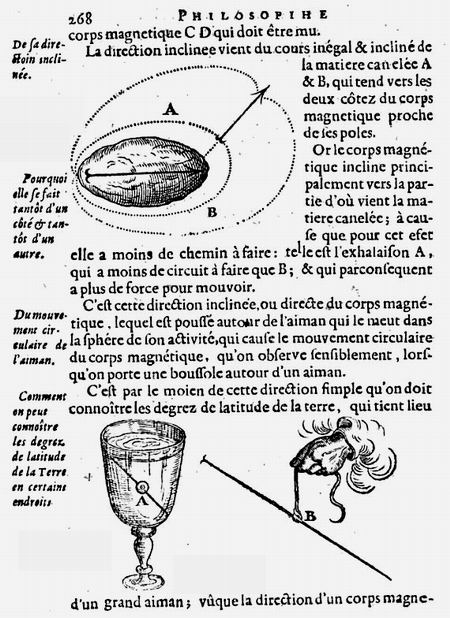
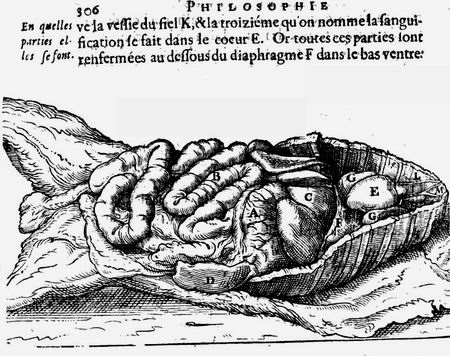
Проф. Playfair замечает, что физика Ньютона проникла в английские университеты под покровом картезианизма. Что касается континента, то картезианцами были Лейбниц, Гюйгенс, Вариньон, Бернулли, Эйлер, Кассини, Маральди, Meран и др. Араго справедливо замечает: "Смотря на такое собрание первоклассных ученых, Маклорэн, думаю, должен был бы воздержаться и не называть гипотезу Декарта рапсодией". В самом деле, ньютонианцами в ту эпоху были Галлей, Котс, Уистон, Грегори, слепой математик Саундерсон и некоторые другие величины, несоизмеримые с указанным блестящим созвездием.

Картезианцы стремились уравновесить "Начала" Ньютона выводом закона тяготения на основании гипотезы вихрей, т. е. построить физическую модель явления тяготения, хотя субъективно они мыслили метафизически, полагая свои модели точной копией действительности. Известно, что сам Ньютон дает в "Началах" основы движения жидкостей в связи с вихревой теорией и выводит заключение, что эта теория не способна объяснить явления мира планет.

Но еще до появления "Начал" Клод Пэрро (Perrault) в "Опыте физики" (1680 г.) вносит видоизменения в теорию вихрей с целью согласования ее с законами Кеплера. Яков Бернулли разрабатывает тот же вопрос. Пьер Вариньон в "Новом предаюложении относительно тяжести" критикует некоторые стороны вихревой гипотезы Декарта, пытаясь улучшить их. Проф. Розенбергер отмечает весьма характерное отношение академических кругов того времени к теории Ньютона.

В "Истории Королевской Академии" (1700 г., стр. 78-100) имеется отчет о работе Вариньона. Из него явствует, что как Вариньон, так и другие члены академии вполне оценивали математическую сторону учения Ньютона, но старались придать теории рационалистический смысл. Лейбнии в "Acta Eroditorum" от 1689 г. (стр. 82) поместил знаменитую работу "Опыт о причине небесных движений" (Tentamen de Motuum Coelestrium causis). Эта работа посвящена критике Ньютона и является началом ссоры между ними. Лейбниц обвинил Ньютона в возрождении "скрытых качеств" перипатетиков. Лейбниц выражает также свое удивление тому, что столь знаменитый математик, как Декарт, никогда не пытался вывести законы Кеплера из своей теории вихрей. Лейбниц сам делает такую попытку, вводя понятие "гармонической циркуляции". Эта попытка не имела успеха, при чем Ньютон в анонимной заметке "Eх epistola cujusdam ad Amicum" [Здесь именно Ньютон обвиняет Лейбница в плагиате исчисления бесконечно малых] отверг циркуляции Лейбница.

Славный Гюйгенс, отец ньютоновой физики, еще в 1661 г. произвел опыт, возбудивший громадное внимание ученого мира. Цилиндрический сосуд вращается вокруг оси. На дне между двумя натянутыми диаметрально нитями находится шарик какого-либо материала. При вращении шарик удаляется к стенкам и остается все время там. При внезапной остановке, когда возникает вихрь жидкости, — шарик перемещается к центру. Для обхода затруднения для случая земли (движение к центру, а не перпендикулярно оси) Гюйгенс выставил дополнительные гипотезы.

В 1690 году вышел знаменитый трактат Гюйгенса о свете (Traite de la lumiere), построенный на гипотезе эфира, в котором имеется приложение: "Рассуждение о причине тяжести". Главная часть была прочитана еще в 1669 году перед Парижской академией. В этой работе Гюйгенс развивает вихревую теорию тяжести, и, кроме того, на основании различия длин секундного маятника, в различных местах земли пытается определить ее форму.

Весь ученый мир Франции с Академией наук во главе долго и упорно стоял на рационалистической точке зрения.

Парижская академия стремилась доказать, что картезианская гипотеза может также быть математически обработана, как и теория Ньютона. Большинство годичных премий было посвящено этому вопросу.

В 1728 году была предложена тема о физическом объяснении тяжести. Премию получил ученый Бильфингер (профессор-академик в Петербурге). Он изобразил тяжесть как результирующую центростремительных сил двух вихрей, имеющих общий центр в земле и пересекающихся перпендикулярно. Тема 1730 г. состояла в объяснении эллиптической формы планетных путей и изменения положения больших осей.

Премию получил Иоанн Бернулли. Он дал картезианскую трактовку вопроса и сделал попытку опровергнуть возражения Ньютона против теории вихрей.

Темы 1732 и 1734 гг. касались взаимного наклонения планетных орбит. Премию получили Иоанн Бернулли и его сын Даниэль, которые рассматривали тяжесть как явление, обусловленное потоком материальных частиц к центру вихря.

В 1733 г. аббат Мольер (Privat de МоНёге) написал картезианские "Лекции по физике", в которых рассматривал "малые вихри". Его ученик Де-Льонуа (La Corgne de Launoy) выпустил "Начала системы малых вихрей или конспект физики аббата Мольера".

Эти "малые вихри “ необходимо считать прямыми предшественниками "малых вихрей" Ранкина, Гельмгольца и Томсона. Яков Кассини написал в 1735 — 36 гг. две работы для доказательства достаточности картезианской гипотезы для объяснения планетных движений. В 1740 году была предложена тема о приливе и отливе. Премию получили Д. Бернулли, Маклорэн, Эйлер и Кавалльери. Био дает следующую характеристику представленных работ:

"Маклерэн – чистый ньютоньянец, Бернулли — ньютоньянец, который просит извинения в том, что он покинул лагерь Декарта; Эйлер — картезианец по смыслу и ньютоньянец по вычислению; иезуит (Кавалльери) — чистый картезианец".

Здесь уже обнаруживаются передом в сторону физики Ньютона. Еще в 1695 г. Лейбниц выпустил работу "Опыт динамики", в которой дано знаменитое различение "живой" и "мертвой" силы. Убедившись в том, что картезианизм приводит к спинозизму и что "без понятия силы нельзя избежать атеизма", Лейбниц перешел на сторону Ньютона, хотя ни разу не упомянул в своей работе имени творца "Начал".

В 1714 г. в Acta Eruditorum появился благожелательный реферат о втором издании "Начал". Во Французской академии старые академики — Мерам, Реомюр, Кассини и др. с Фонтенелем во главе — "с истинно римской твердостью" отстаивали учение Декарта. Старый 95-летний Фонтенель даже в 1752 г. выпустил "Теорию картезианского вихря“. Более молодые академики — Мопертюи и Клеро — начинали уже свыкаться с идеями Ньютона.

Клеро в 1743 году в знаменитом сочинении о "Фигуре земли" допустил в частицах притягательную силу, хотя в угоду картезианцам пытался развить различные гипотезы тяготения. Мопертюи в 1732 году представил мемуар на ту же тему. В нем он делает следующее характерное заявление: "Я никоим образом не исследую, согласуется ли притяжение со здравой философией или же противоречит ей. Я здесь рассматриваю его только как математик (geometre), т. е. как свойство, проявления которого (какова бы ни была их действительная сущность) можно исчислить, ибо мы полагаем это свойство равномерно присутствующим во всех частицах материя и действующее пропорционально ее количеству".

В "Истории Королевской Академий" (1732 г., стр. 112) появился отчет об этой работе Мопертюи. В ней указывается: "Необходим был гений и великий авторитет Ньютона, чтобы снова ввести в физику притяжение, откуда оно было изгнано Декартом и его последователями или лучше всеми философами и при всеобщем одобрении. Оно возвращается, однако, несколько переодетым, ибо, если угодно, это совсем не притяжение в собственном смысле слова, а скорее название, которое дано неизвестной причине. Эта причина сравнивается и рассматривается, чтобы, по крайней мере, знать ее способ проявления, при чем ожидают, что однажды и сама ее природа сделается доступной познанию. С этой точки зрения и с такой мудрой предусмотрительностью вводят Ньютон н его ученики это притяжение".

Из этого отрывка ясно, что ученый мир уразумел, наконец, действительный смысл теории Ньютона. Не верно лишь то, что будто бы ученики Ньютона обнаружили здравый смысл учителя — наоборот, они старались запутать посторонними соображениями ясную доктрину Ньютона. Позднейшие мыслители также не обнаружили благоразумия академических кругов 1732 года и еще до сих пор спорят об истинном смысле учения Ньютона. Победа этого учения ясно обозначилась к 1740 году, когда в „Phil. Transact" (Iul, n° 457 p. 409) появилась статья P. Sigorgn’a "Физико-математическое доказательство невозможности и недостаточности вихрей".

"С тех вор, — говорит Розенбергер, — картезианизм был как будто вырван с корнем из почвы естественных наук. Он сделался, как раньше слово схоластика, общим понятием, всего плохого, существенным обозначением всего, естественно-научно бесплодного, устрашающим примером фантастического философствования, пугалом, которым стращают больших и малых ребят науки". Все это продолжалось до тех пор, пока движение самой науки не возродило картезианизм в еще большем блеске, чем раньше.

— 2 —

Возрождение картезианской физики необходимо отнести к 1858 году, когда в журнале Crell’я появился мемуар Гельмгольца: "Об интегралах уравнений гидродинамики, соответствующих вихревым движениям".

Но и до этого момента рациональное течение в физике давало значительные результаты: вспомним только о работах Юнга (1773 — 1829), Френеля (1788 — 1827), Навье (1785 — 1836), Коши (1789 — 1857), Пуассона (1781 — 1870), Гамильтона (1805 — 1865), Стокса (1819 — 1903), Мак-Куллоха (1809 — 1847) по теории света на основе теории электричества, которые Максвелл впоследствии облек лишь в математическую форму. Но эфир этих ученых не был картезианским эфиром — чистым протяжением (из движения частей которого и необходимо вывести все явления). Этот эфир был упругим, твердым телом, с весьма странными свойствами, которые являются именно главными аргументами против существования эфира.

Картезианский эфир еще не проник в область оптики и электромагнетизма, скрыто существуя в виде "идеальной жидкости гидродинамики". Законы движения этой жидкости, т. е. "пространства-материи" Декарта были впервые формулированы Эйлером в так называемых уравнениях Эйлера:

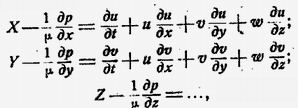
где X, Y, Z — составляющие (прямоугольные) внешней силы (или результирующей всех таких сил), p — давление в идеальной жидкости, μ — плотность, u, v, w — слагающие скорости частиц. Уравнения Эйлера показывают, что происходит в известной точке (x, y, z) пространства с течением времени, т. е. определяют скорости, как функции x, y, z, t. Но Эйлер также поставил вопрос иначе: что происходит с течением времени с известной частицей, координаты которой в момент t = 0 равны начальным значениям x₀ , y₀ , z₀ .

Лагранж в знаменитой "Аналитической механике" ответил на этот вопрос в изящной форме уравнений Лагранжа:

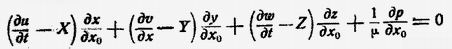
и т.д., где x, y, z, p — функции x₀ , y₀ , z₀ , т. е. начального положения частицы.

До Гельмгольца исследовалось движение жидкости, в котором слагающие скорости имеют потенциал, иначе являются производными некоторой функции φ:

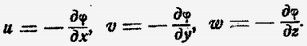
Это движение Лагранж назвал движением с потенциалом скоростей, указав, что этот потенциал существует в случае действия сия, имеющих потенциал (например, силы тяжести). Так как сила трения зависит от скорости, иначе говоря, не имеет потенциала [напомним, что потенциал в обычном смысле это — функция, зависящая только от положения, но не от скоростей и ускорений.], а идеальная жидкость определяется как жидкость без трения, то движение этой жидкости рассматривалось как движение с потенциалом скоростей, при чем под действующей силой подразумевалась сила тяжести.

Согласно указанию Гельмгольца, в основном мемуаре (стр. 6 русского перевода) Эйлер впервые обратил внимание на движение жидкости, при которых не имеет места потенциал скоростей, например, вращение жидкости около оси, при одинаковой угловой скорости всех частиц. "К силам, способным вызвать такого рода движения, принадлежат силы магнитные, действующие на жидкость, по которой пробегает электрический ток, и в особенности трение частиц жидкости между собой и о твердые тела".

Очевидно, что слагающие скоростей f, g, h должны в таких случаях быть связанными каким-либо образом с угловыми скоростями частиц.

Действительно, еще в 1845 году Стокс показал, что слагающие угловых скоростей частиц f, g, h выражаются следующими функциями от скоростей u, v, w:

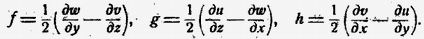
Если вращения нет, то f, g, h = 0 и

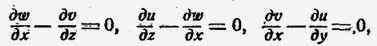
а это именно и есть условие существования потенциала скоростей. Продифференцировав уравнения и т.д. получим, условия существования потенциала.

Кроме того, тому же Стоксу принадлежит следующее общее математическое соотношение между интегралом вектора вдоль некоторой линии С и интегралом по поверхности S, для которой эта линия является контуром. Пусть u, v, w — слагающие некоторого вектора A; тогда по теореме Стокса:

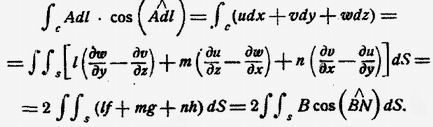
Если A — вектор скорости, то интеграл

=

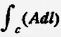
называется циркуляцией (понятие, введенное В. Томсоном) скорости вдоль линии.

Вектор В (f, g, h) есть вектор угловой скорости или, по Гельмгольцу, — вихрь; соответствующий интеграл называется потоком вихря. Таким образом, теорема Стокса гласит: циркуляция скорости вдоль линии равна потоку вихря сквозь поверхность, для которой линия служит контуром.

Гельмгольц доказал следующие основные теоремы:

1) ни одна частица жидкости не может придти во вращательное движение, если только она не обладала им уже с самого начала;
2) частицы жидкости, расположенные для какого-либо момента времени на вихревой линии, всегда будут при своем перемещении принадлежать одной и той же вихревой линии;
3) произведение поперечного сечения на скорость вращения для бесконечно тонкой вихревой трубки (нити) на всем ее протяжении постоянно и сохраняет свою величину при передвижении нити; поэтому вихревые нити должны внутри жидкости замыкаться на себя; они могут оканчиваться не иначе, как только на ее границах.

В математической форме теоремы Гельмгольца выражаются уравнением:

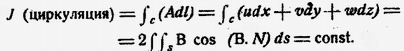
В этой форме закон Гельмгольца сформулирован Томсоном, Гельмгольц дал вывод, основанный на известной теореме Грина:

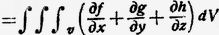
выражающий интеграл по поверхности S через интеграл по объему V, который ограничивает эту поверхность. Из уравнений для f, g, h получаем: следов.

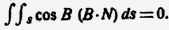
Применив это уравнение к отрезку бесконечно тонкой вихревой трубки (нити) с сечениями S₁ и S₂ мы получим

B₁S₁ = B₁S₂ = const

Полагая const = 0, получим: B₁S₁ = B₁S₂ .

Подчеркнем, доказательство теоремы Гельмгольца основано на предположении, что действующие силы имеют потенцал. Между тем, помимо сил трения, вся электродинамика обнаруживает силы, не имеющие обычного потенциала. Вот почему в области электродинамики мы имеем дело с постоянным возникновением и уничтожением электромагнитных вихрей. Сам процесс получения электрического поля посредством "трения" весьма характерен.

Адамар, Шютц, Бьеркнесс, Зильберштейн вообще показали, что не при всяких условиях выполняется теорема Гельмгольца о сохранении вихрей. Особенно интересны явления удара, т. е. относительной прерывности, на которые указывают Адамар и сам Гельмгольц (работа: "О прерывном движении жидкостей"); нам кажется, что именно в таких "относительно прерывных“ действиях и лежит ключ к пониманию многих явлений природы, что хорошо подтверждается теорией квантов. Как бы там ни было, но с точки зрения диалектики очевидно, что вихревая теория, как и всякие другие, подлежит закону развития. Пройдет известный период времени, и научная мысль даст новое усовершенствование учения, которое будет иметь тот же (если не больший) коэффициент, что и теперешняя теория в отношении к теории эпохи Декарта.

Теорию циклических (моно- и полициклических) движений в непрерывной среде разрабатывал Гельмгольц; попытку построить картезианскую механику на рациональной основе сделал Г. Герц. Как указывает Гельмгольц в предисловии к "Механике" Герца, эта механика, которая при своем появлении оказала незначительное влияние на научную мысль, еще будет иметь большое значение. Попытку построить механику "прерывностей" сделал P. Appel. В последнее время М. Born выпустил "Vorlesungen uber Atommechanik", представляющее собою механику прерывности применительно к теории квантов. См. также "Основания новой квантовой механики". Сборник. Гиз. 1927 г.

— 3 —

Вихревую теорию материи разрабатывает целый ряд крупнейших ученых, из которых на первое место необходимо поставить Вильяма Томсона-Кельвина и Дж. Дж. Томсона. Вслед за статьей о вихревых атомах В. Томсон опубликовал большую работу о "Вихревом движении" (1869). "Математическая задача этой работы — иллюстрировать гипотезу о том, что пространство непрерывно заполнено несжимаемой без трения жидкостью, на которую не действуют никакие внешние силы и что материальные явления всякого рода зависят исключительно от движения в этой жидкости “ (стр. 13, IV т. соч. Томсона).

Здесь, между прочим, Томсоном введено понятие циркуляции и дано новое доказательство теоремы Гельмгольца. В 1875 г. появилась работа "Статика вихря" (Vortex statics), в которой дан анализ устойчивости вихревого шнура. Большое значение имеет статья "Колебания цилиндрического вихря". Некоторые результаты этой работы мы пояснили в примечаниях к статье Томсона о вихревых атомах. Анализ задачи о максимуме и минимуме энергии вихревого движения дан Томсоном в статье того же названия. Особенно важен мемуар "Распространение плоского движения в волнующейся невязкой жидкости" (*), в котором Томсон доказывает, что распространение плоской волны в вихревой трубке совершается согласно тому же уравнению, что и световые колебания в эфире, рассматриваемом как упругое твердое тело.

(*) Phil. Mag. V. 24. Соч. IV. Под "слоистым движением" (laminar motion) здесь разумеется движение согласно уравнения m : u = 2μy , v = 0 , w = 0 и, следовательно, f = 0 , g = 0 , h = –μ; "бурлящая невязкая жидкость" это — вихревая губка (vortex sponge). Как видно из этих уравнений, "слоистое движение" заключается в том, что жидкость разделяется на слон, при чем скорость каждого слоя зависит от его расстояния от оси х-ов (u = 2μy); кроме движения вдоль этой оси, частицы имеют вращение h = –μ, т. е. вокруг мгновенных осей параллельных z (вихри).

Томсон доказывает, что, если мы имеем вихревую губку, заключенную между двумя плоскостями, параллельными плоскости xy и в некотором месте возникает слоистое движение, обозначаемое им через f(y,0,0) для момента t = 0 , то уравнение распространения слоистого движения будет: , где R — "средняя скорость бурлящей жидкости" (особо определяемая величина). Это уравнение, как известно, изображает распространение электромагнитных волн и вообще колебания в упругом твердом теле.

Здесь обнаруживается замечательная аналогия с распространением плоско поляризованной электромагнитной волны. Мы уже указывали» что вектор u аналогичен электрическому току, вектор h — магнитной силовой линии; следовательно, можно было бы a priori утверждать аналогию между волновыми процессами в вихревой среде и процессами в электромагнитном ноле. Теория подтверждает это заключение.

Обратим еще внимание на открытый Томсоном так называемый "skin effect" (поверхностный эффект, эффект Кельвина): при переменных токах большой частоты токи эти образуют "слоистое движение", т. е. располагаются главным образом на поверхности проводника, — сила тока уменьшается по направлению к центру. Это явление известно всем электротехникам, и для таких случаев проводники изготовляются полыми.

Другие работы Томсона — не станем их перечислять — касаются формы вихревых шнуров, их взаимодействия, электромагнитных аналогий. Им же разрабатывалась теория гиростатов, даны модели: гиростатического компаса, силы упругости, колебаний и волн в цепи гиростатов. Томсон возродил известную теорию тяготения Лесажа на основании свойства упругости вихревого атома.

Дж. Дж. Томсон опубликовал фундаментальный трактат по теории вихрей: "Оп the motion of vortex rings" (London, 1883). В примечаниях к статье В. Томсона-Кельвина мы привели некоторые результаты этой работы [см. В. Кельвин. О вихревых атомах]. Общая задача работы Дж. Дж. Томсона — исследовать, насколько вихревые гипотезы пригодны для построения абсолютной кинетической теории материи. С этой целью Томсон подверг анализу различные формы вихрей, их взаимодействие и колебательные движения. В частности, Томсон доказал устойчивость вихревого кольца в отношении сохранения форм оси, исследовал взаимодействие материального шара и кольца. В связи с теорией вихрей Дж. Дж. Томсон предпринял в 1888 г. попытку построить адинамическую механику. Эта попытка изложена в работе "О некоторых приложениях динамических принципов к физическим явлениям". Здесь мы встречаем обобщенный закон инерции, который Г. Герц положил в основу своей картезианской "механики" (*).

(*) Дж. Дж. Томсон вводит этот закон для рассмотрения брахистохронического движения в n-мерной форме, которую Г. Герц наглядно изобразил как n-мерное пространство. Еще lacobi в 1841 г. рассматривал динамические проблемы, как брахистохронические; Liouville (Sur les equations de la dynamique. C. R. 1892) показал, что каждая динамическая проблема может быть сведена к проблеме геодезической линии. См. A. Voss. Enc. d. Mat. Wiss. т. IV. Ср. с общей теорией относительности, в которой основную роль играет "геодезическая линия".

Цель Томсона, как и Г. Герца, — свести понятие потенциальной энергии к понятию кинетической и всякую "силу" рассматривать как ускорение, т. е. приращение количества движения в единицу времени.

Томсон вводит понятие киностеничееких координат (Томсон и Тэт называют их ignored, Гельмгольц и Герц — verborgene), с целью обозначения тех движений, которые дают в итоге так называемую "потенциальную энергию": массы и движения, образующие механизм потенциальных сил, Гельмгольц-Герц назвали скрытыми массами и скрытыми движениями. Согласно вихревой гипотезе, такими массами и движениями являются массы и движения вихрей и окружающей идеальной жидкости (пространства).

Ограниченность места не позволяет нам дать обзор работ других выдающихся ученых по теории вихрей. Полный обзор читатель найдет у Winkelman'a, Lamb'a и в статье A. Love’a. J) В частности, Винкельман дает ценные сведения, касающиеся опытного получения и наблюдения вихрей. Оказывается, что не только теория солидно обоснована, но что выводы теории касательно основных свойств вихрей подтверждаются в существенном на опыте.

Но мы хотим обратить внимание читателя на другое замечательное обстоятельство, а именно на то, что важнейшая и обширнейшая область науки о природе — область электромагнетизма и оптики прямо толкает к вихревой теории материи. Этот замечательный факт очень рельефно обнаруживается в простом обзоре развития теории Максвелла.

Эту теорию изображают обычно, как "непонятную", как скрижали завета, свалившиеся с неба. Но если обратиться к календарным датам, то получается иная картина. В 1855 году Максвелл опубликовал известный мемуар о "Фарадеевых силовых линиях", в котором ему еще не удалось построить желательную модель электродинамических сил. В 1856 г. В. Томсон пришел к заключению, что магнитные силы имеют вихревой характер. В 1858 г. Гельмгольц опубликовал знаменитый трактат о вихревом движении, а в 1861 – 1862 гг. появилась, наконец, известная модель электромагнитного поля Максвелла в которой ток рассматривается как поступательное движение, а магнетизм, как вихревое.

В 1864 году появилась "Динамическая теория электромагнитного поля", в которой Максвелл подробнее развивает взгляды, изложенные в предыдущих мемуарах. Наконец, в 1871 году появился знаменитый трактат "Электричество и магнетизм". Одна из самых замечательных глав (21 глава II тома), связанная с электромагнитной теорией света, посвящена выяснению действия магнитов на свет. Максвелл ссылается на работу Томсона (1836), Ранкина (1849 – 1850) и, наконец, Гельмгольца (1858). Математическое исследование вопроса (§ 22. Гипотеза молекулярных вихрей) базируется на работе Гельмгольца.

Заметим здесь, что та теория Максвелла, которой мы пользуемся ныне, построена по методу Ньютона. Убедившись, что проблема рационального истолкования электромагнитных явлений слишком сложна, Максвелл, подобно Ньютону, перешел к относительно формальной трактовке вопроса на основе механики Лагранжа. Но всякий, исследующий развитие учения Максвелла, ясно видит, что "физические модели" послужили именно путеводной нитью, которая вывела ученого из лабиринта природы.

Необходимо отметить, что модели Максвелла не носят чисто кинетического, т. е. рационального характера — эфир Максвелла напоминает еще обычное тело. Лишь В. Томсон впервые в 1880 году предложил адинамическую модель эфира, так называемую "вихревую губку", т.е. "идеальную жидкость", в которой равномерно распределены вихревые и невихревые области. В 1883, 1885 и 1889 годах появились работы Томсона по этому же вопросу. В 1885 году Фицджеральд обсуждал проблему устойчивости этого "гиростатического эфира".

В этом же году Гикс рассматривал распространение волн в гиростатическом эфире. Теория такого распределения дана Томсоном в 1887 году, о чем уже было упомянуто выше. Другие модели подобного же рода были даны Гиксом в 1888 и 1895 годах, Фнцжеральдом в 1899 году. Все эти модели, как и другие, подвергаются суровой критике, при чем критики из всех сил стараются доказать, что теория эфира не соответствует "действительности" и что, следовательно, эфир это — "математическая фикция". Но нет худа без добра. Критика представлений об эфире показала, во-первых, что эфир не является физическим телом в обычном смысле слова и что, следовательно, не теория упругости должна объяснить свойства эфира, а, наоборот, теория упругости должна быть построена на основании понятая эфира, что и выполняется вихревой теорией; во-вторых, выяснила действительное значение физической теории и физических моделей.

— 4 —

Развитие физики, в частности учение об электромагнетизме и свете, все больше и больше выясняет тот факт, что картезианское понимание эфира, как физического пространства, является правильным. Еще Ньютон в известных "Вопросах" оптики указал, что хотя волновая теория света в обычном смысле слова объясняет многое, но свет все же не является обычным волновым движением, что это скорее синтетическое явление волнового и корпускулярного одновременно характера.

Теория квантов подтвердила это гениальное предвидение Ньютона, показав необходимость какого-то особенного, пока еще не вполне ясного, представления о явлениях света и сущности "световых волн". Вихревая теория материи прямо намекает на то, чем является синтез волнообразной и атомной теории света.

В самом деле, если электрические и магнитные силовые линии — это вихревые образования, а свет — электромагнитное колебания, распространяющееся со скоростью света, то известная вихревая система, обладающая, как мы видели, свойством упругого колебания и несущаяся в пространстве со скоростью света, дополняет именно обычное представление о свете до того синтетического представления, к которому пришла наука. Свет имеет атомное строение постольку, поскольку вихри образуют "атомы" в непрерывной среде, но свет это — непрерывное явление постольку, поскольку вихревой атом может существовать только в определенной материальной субстанции и является тем или иным вихревым образованием.

В замечательной книге Дж. Дж. Томсона "Электричество и материя" наглядно показана непрерывная система электромагнитных (световых) колебаний: при ускоренном движении электрического заряда вихревые нити, образующие его электрическое поле, дают "электромагнитные волны". Но если эту картину дополнить представлением об "изолированной“ вихревой системе, несущейся в пространстве со скоростью света и обладающей известным колебательным движением, то мы и получим "атом света".

А. Эйнштейн в статье "О развитии воззрений на сущность и строение лучеиспускания" говорит: "Поскольку мне известно, еще не удалось создать математическую теорию изучения, которая одновременно удовлетворяла бы и волновому строению изучения и атомному". Замечание правильное, и, быть может, пройдет еще немало времени, пока такая теория будет создана, и мы получим, наконец, некоторое рациональное представление о явлениях света.

Но путь к такому представлению, несомненно, идет через вихревую теорию материи. Эта теория является компасом, указывающим путь. Она указала путь Максвеллу, укажет путь будущим строителям рационального учения об электромагнитных волнах. В этом именно основное значение вихревой теории, а не в том, что она должна будто бы быть точной копией реальности.

Если сравнить содержание статьи В. Томсона о вихревых атомах с теми заключениями о строении атома, к которым пришло современное знание, то может показаться, что вихревая теория "устарела". Но такое заключение совершенно не верно. Оно основывается на ложном, метафизическом понимании значения физической теории. Что необходимо сказать о на основании того, что геометрический круг не соответствует реальному, стал бы отрицать значение геометрии. Между тем рациональная физика и является геометрией физического мира, подобно тому, как геометрия это — элементарная физика.

Такое понимание значения геометрии и физики (рациональной) было выдвинуто Декартом. В этом сущность Декартовской теории "врожденных идей" — учения, которое, по справедливому замечанию Плеханова (предисловие к Л. Фейербаху), не было понято современниками философа (псевдокартезианцами), в частности Локком, и не понято до сих пор. Декарт поставил тот же вопрос, что и Кант: как возможно синтетическое познание a priori, в частности математика?

Декарт ответил на этот вопрос ... так: наш мир — продукт длительной эволюции. Следовательно, человек и его орган познания — мозг — образовались в течение громадного промежутка времени, выделившись из мировой материальной среды, согласно законам движения этой среды. Отсюда Декарт заключил, что мозг, порожденный мировой материей, должен адекватно соответствовать этой материи. В этом именно основание рационализма Декарта, в этом именно значение его аксиомы простых, ясных и отчетливых идей.

Декарт полагал, что наши основные понятия пространства, движения, времени ("простые, ясные и отчетливые идеи") не случайны, а являются продуктом "фундаментального опыта эволюции". Иначе говоря, основные формы, в которые облекается наше познание, имеют корни в самой природе, из которой выделился наш мозговой аппарат. Но Декарт, как и Кант (начавший, как известно, с „Всеобщей истории и теории неба"), запутали свои учения под давлением теологических сил, в результате чего глубоко материалистические теории познания превратились в идеалистические, а "натуралистическое“ учение о "врожденных идеях" — в платоновско-мистическое.

Отсюда ясно картезианское понимание значения геометрии и рациональной физики: они дают нам основные формы материальных процессов; геометрия и рациональная физика это, так сказать, науки о "деталях“ "вселенской машины". Сама "машина" бесконечно сложна, но, как бы она ни была сложна, она состоит из простых деталей в самых разнообразных комбинациях, бесконечной даже сложности. В этом именно значение физических моделей, в частности вихревой теории.

Нет необходимости, чтобы они были точными копиями действительности, и принципиально важно то, что они показывают возможность рационального объяснения явлений. Реальная материя обнаруживает силы тяготения, упругости, электромагнитные и т. д.; если эти силы находит свое рациональное объяснение в физической модели, то этим сделано очень многое, хотя действительное явление может быть гораздо сложнее.

Пуанкаре в своей характеристике "Физики принципов" (см. "Ценность науки") приводит пример машины, передаточный механизм которой скрыт, но в которой видны точки приложения двигательной силы и сопротивления. Этот передаточный механизм может состоять из громадного количества "сцепленных деталей", но каково бы ни было их количество, "физическая модель" механизма дает основные детали сцепления и в этом смысле вполне эквивалентна данному механизму. Так что правильно построенная физическая модель в известной мере соответствует реальности.

Заметим здесь, что основное условие рациональной модели в том, чтобы она не базировалась на том, что требуется объяснить. Вот почему модели Максвелла, Больцманна или Бьеркнесса, например, не являются вполне рациональными; таковой является вихревая теория материи, — вот почему она и вызвала такой научный энтузиазм и внимание.

В заключение укажем, что относительно формальное изучение явлений дает возможность построения модели, что в свою очередь толкает вперед формальное познание явлений.

Так, формальный закон тяготения Ньютона привел Римана к построению рациональной теории притяжения на основании гидродинамических понятий "источников" и "стоков". Эта теория Римана была использована Гербером, который с помощью учения Гельмгольца – Неймана о кинетическом потенциале, дополнил закон Ньютона и получил известную формулу движения перигелия Меркурия.

Точно также формальные законы электромагнетизма указывают на известный механизм сил, а вихревая теория помогает решать некоторые вопросы электрической теории материн (см. предисловие Пуанкаре к его "Теории вихрей").

Таким образом, истинно научный метод заключается в сочетании рационального и формального моментов, при чем как тот, так и другой являются только относительными.

[Заключение автор смазал. Столько проникновенных слов сказал во славу модельного, рационально-конструктивного метода, а в конце плеснул в бочку мёда ложку дёгтя — несколько "формальных моментов". Наверное, кто-то его принудил это сделать — уж больно неискренне выглядят последние короткие абзацы. Возможно, он писал их на коленке в кабинете своего начальника. — О.А.]

---

Материал сверстал и разместил в Сети Олег Акимов 12 декабря 2014 года