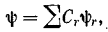Квантовая механика: её история и суть

Альберт Эйнштейн против квантовой механики

• Можно ли считать квантовомеханическое
  описание физической реальности полным?
• Теория квантов и основы физики
• Квантовая механика и действительность
• Элементарные соображения по поводу
  интерпретации основ квантовой механики
• Вводные замечания об основных понятиях

ВСТУПИТЕЛЬНАЯ СТАТЬЯ В. А. ФОКА

("Успехи Физических Наук", 1936, Т. XVI, вып. 4, с. 436 – 440)

В квантовой механике мы сталкиваемся с новыми физическими идеями, настолько отличными от привычных представлений классической теории, что освоение их представляет значительные трудности, особенно для умов, воспитанных на классической физике. Насколько трудно таким умам "принять" эти новые идеи, показывает то, что даже создатель теории относительности — Эйнштейн,—обогативший человеческую мысль не менее глубокими физическими идеями, и, как это ни парадоксально, один из создателей квантовой механики — Шредингер — до сих пор не могут примириться с теми следствиями, которые вытекают из открытия квантовой механики.

В течение 1935 г. в американском журнале Physical Review появились две статьи под одинаковым заглавием, которые мы приняли и в качестве заголовка настоящей объединенной статьи. Первая статья написана Эйнштейном, Подольским и Розеном. В ней авторы, исходя из некоторого "критерия физической реальности", приходят к выводу, что на вопрос, поставленный в заголовке, приходится ответить в отрицательном смысле. В ответ на эту статью в одном из следующих номеров того же журнала появилась вторая из упомянутых статей, написанная Бором. В ней автор, развивая неоднократно высказанные им ранее идеи, дает глубокий и блестящий анализ понятия физической реальности в свете новой, квантовой физики. Пользуясь самыми простыми средствами, Бор дает исчерпывающее разъяснение парадоксу, указанному Эйнштейном, Подольским и Розеном, и показывает, что на вопрос, поставленный этими авторами, следует ответить в положительном смысле.

Хотя в споре между авторами названных двух работ и не было высказано ни одной существенно новой идеи, и хотя ответ на поставленный в первой статье вопрос, совпадающий с ответом Бора, непосредственно вытекает из соображений, которые можно найти даже в курсах квантовой механики [1], — тем не менее этот спор представляет большой принципиальный интерес ввиду того, что в нем с большой ясностью были формулированы точки зрения обеих сторон, вследствие чего он в большой мере содействовал выяснению для многих физиков тех новых физических понятий, которые связаны с квантовой механикой.

Ввиду того интереса, который представляют указанные две статьи, мы печатаем здесь их полный перевод. Мы не приводим статьи Шредингера [2], посвященной тому же вопросу, так как в ней развиваются лишь парадоксы, вытекающие из неправильной точки зрения Эйнштейна, Подольского и Розена, а ответа на них не дается. Так же точно мы не приводим и других работ, появившихся в связи с упомянутым спором, и в частности работы Ферри [3], содержащей ценные математические пояснения к рассуждениям Бора. Мы можем ограничиться двумя основными статьями потому, что ими исчерпывается сущность спора: в статье Эйнштейна, Подольского и Розена весьма четко формулирована естественная, хотя и оказавшаяся неправильной точка зрения и указаны те парадоксы, к которым она приводит, а в статье Бора дано исчерпывающее разъяснение этих парадоксов на основе введенного им понятия "дополнительности".

Полемику между Эйнштейном, Подольским и Розеном, с одной стороны, и Бором, с другой, можно, если угодно, рассматривать как спор о физическом смысле волновой функции. Приступая к изложению математической части своих рассуждений, Эйнштейн [в дальнейшем мы будем, для краткости, опускать фамилии двух других соавторов] говорит, что основным понятием теории является понятие состояния, описываемого волновой функцией. Эйнштейн понимает слово "состояние" в том смысле, какой ему обычно приписывается в классической физике, т. е. в смысле чего-то вполне объективного и совершенно независящего от каких бы то ни было сведений о нем. Отсюда и проистекают все парадоксы. Квантовая механика действительно занимается изучением объективных свойств природы в том смысле, что ее законы продиктованы самой природой, а не человеческой фантазией. Но к числу объективных понятий не принадлежит понятие о состоянии в квантовом смысле. В квантовой механике понятие о состоянии сливается с понятием "сведения о состоянии, получаемые в результате определенного максимально-точного опыта". В ней волновая функция описывает не состояние в обыкновенном смысле, а скорее эти "сведения о состоянии". Эйнштейн показывает, что, не трогая системы, можно придать ее волновой функции тот или иной вид. Если считать вместе с Эйнштейном, что волновая функция описывает объективное состояние, то, конечно, его результат будет иметь характер парадокса. Ведь невозможно себе представить, чтобы объективное состояние системы (что бы мы под этим ни подразумевали) менялось в результате каких бы то ни было операций, произведенных не над ней, а над другой системой, которая с ней вовсе не взаимодействует. Но хотя в результате таких операций не может меняться "объективное состояние" системы, зато могут меняться "сведения о состоянии", т. е. состояние в квантовом смысле. Поэтому все парадоксы исчезают, коль скоро мы откажемся от проводимого Эйнштейном неверного "объективного" толкования волновой функции и примем правильное ее толкование, т. е. будем считать, что она описывает "состояние в квантовом смысле" или "сведения о состоянии, получаемые в результате определенного максимально-точного опыта".

Под максимально точным опытом мы разумеем такой, который позволяет найти все те величины, какие вообще могут быть известны одновременно. Это определение применимо как к классической, так и к квантовой механике. Но в классической механике максимально-точный опыт был по существу один, а именно тот, который давал значение вообще всех механических величин, в частности координат и составляющих количества движения. Именно потому, что в классической механике любые два максимально-точные опыта дают те же самые сведения о системе, и можно было говорить там о состоянии системы, как о чем-то объективном, не оговаривая, путем какого именно опыта получены сведения о нем.

Иначе обстоит дело в квантовой механике. Там такого рода оговорка существенно необходима. Действительно, соотношения Гейзенберга показывают, что разные опыты могут друг другу мешать. Поэтому и максимально точных опытов может быть бесчисленное множество: одни из них будут давать максимально-точные сведения о координатах, другие — о количестве движения, и т. д. Каждому результату определенного максимально-точного опыта сопоставляется в квантовой механике волновая функция. Она представляет, таким образом, запись сведений, получаемых в результате такого опыта. С этой точки зрения легко понять и физический смысл зависимости волновой функции от времени, т. е. физический смысл уравнения Шредингера: оно позволяет использовать сведения, относившиеся к начальному моменту времени, для предсказаний, относящихся к позднейшим моментам времени.

Мы уже говорили выше о том, что в квантовой механике стирается грань между понятиями "состояние" и "максимально-точные сведения о состоянии". Это утверждение представляет лишь иную формулировку той мысли, которую имеет в виду Бор, когда говорит о необходимости "радикального пересмотра наших взглядов на проблему физической реальности". Эта мысль блестяще обоснована Бором в его статье. Поэтому мы можем не останавливаться на ее обосновании, а перейти к анализу некоторых следствий, вытекающих из толкования волновой функции как записи сведений.

Прежде всего, сведения о системе не обязаны быть максимально-точными. Это значит, что система не обязана иметь определенную (хотя бы неизвестную) волновую функцию. Может, например, случиться, что мы знаем о количестве движения частицы только то, что оно равно либо p₁ (с вероятностью w₁), либо p₂ (с вероятностью w₂), и ничего не знаем о ее координатах. Из этих сведений мы никакой волновой функции построить не можем, а можем только построить (по Нейману [4]) некоторый "статистический оператор", который позволяет вычислить вероятности и математические ожидания для всех механических величин, соответствующие имеющимся сведениям.

Таким образом с максимально-точными сведениями о системе мы можем сопоставить волновую функцию (это будет так называемый случай чистого состояния, reiner Fall), а с менее точными сведениями мы волновую функцию сопоставить не можем (это будет так называемый случай смеси состояний, Gemisch).

С этим обстоятельством связана характерная особенность квантово-механического описания сложной системы, состоящей из двух или нескольких подсистем (случай, рассмотренный Эйнштейном).

Предположим, что наша система состоит из двух подсистем. Координаты (или другие переменные) первой подсистемы обозначим через x₁, a координаты второй подсистемы — через x₂. Пусть над полной системой произведен максимально-точный опыт, который дал нам ее волновую функцию Ψ(x₁, x₂). В таком случае, хотя сведения о полной системе и будут максимально точными, но сведения о подсистемах, вообще говоря, не будут таковыми. То есть Ψ(x₁, x₂) не распадается на произведение вида ψ(x₁) ψ(x₂).

Поэтому, даже если обе подсистемы перестали взаимодействовать, мы не вправе приписывать им в отдельности каких бы то ни было, хотя бы и неизвестных, волновых функций (Эйнштейн, по-видимому, думал обратное [он говорит: "Мы не можем, однако, вычислить того состояния, в котором каждая из двух систем останется после взаимодействия"]. Мы можем только приписать им статистические операторы, которые легко выражаются через Ψ(x₁, x₂).

и соответственно для второй подсистемы

Чтобы получить максимально-точные сведения об отдельных подсистемах, т. е. чтобы определить их волновые функции, мы должны произвести еще один опыт. Знание волновой функции Ψ(x₁, x₂) вносит здесь то упрощение, что этот опыт достаточно произвести над одной из подсистем.

Этот процесс и рассматривается Эйнштейном. Из того, что здесь сказано, достаточно ясно, что лишь неправильное толкование физического смысла волновой функции привело его к заключению о неполноте квантово-механического описания. С еще большей ясностью неправильность этого заключения вытекает из глубокого анализа Бора. Поэтому мы надеемся, что у внимательного читателя не останется сомнений в том, кто прав в том споре, которому посвящена эта статья.

---

1. См. например, W. Pauli, Die allgemeinen Prinzipien der Wellenmechanik, Handb. d. Physik. Geiger u. Scheel, Berlin 1933.
2. E. Schrödinger, Proc. Cambr. Phil. Soc, 31, 555, 1935.
3. W. Furry, Phys. Rev., 31, 393, 1935
4. См. например, J. V. Neumann, Mathemafischi Grün Hagen der Quantenmechanik, Springer, Berlin, 1932.

Можно ли считать квантовомеханическое
описание физической реальности полным?

А. Эйнштейн, Б. Подольский, Н. Розен, 1935 г.,
СНТ, т. 3, с. 604 – 611; УФН 1936 XVI 4, с. 440 – 446.

В полной физической теории существует определенный элемент, соответствующий каждому элементу реальности. Достаточным условием реальности той или иной физической величины является возможность предсказания ее с достоверностью, не нарушая системы. В квантовой механике в случае двух физических величин, описываемых не-коммутирующими операторами, знание одной из этих величин делает невозможным знание другой. Тогда, либо 1) описание реальности в квантовой механике с помощью волновой функции является неполным, либо 2) эти две физические величины не могут одновременно обладать реальностью. Рассмотрение проблемы предсказания поведения некоторой системы на основе измерений, выполненных над другой системой, которая предварительно взаимодействовала с рассматриваемой, приводит к результату, что если утверждение «1» неверно, то утверждение «2» также неверно. Таким образом, это приводит к заключению, что описание физической реальности с помощью волновой функции является неполным.

– 1 –

При анализе физической теории необходимо учитывать различие между объективной реальностью, которая не зависит ни от какой теории, и теми физическими понятиями, с которыми оперирует теория. Эти понятия вводятся в качестве элементов, которые должны соответствовать объективной реальности, и с помощью этих понятий мы и представляем себе эту реальность.

Для суждения об успехе физической теории мы можем задать себе два вопроса: 1) Правильна ли теория? и 2) Является ли даваемое теорией описание полным? Только в том случае, если на оба эти вопроса можно дать положительные ответы, концепции теории могут быть признаны удовлетворительными. Первый вопрос — о правильности теории — решается в зависимости от степени согласия между выводами теории и человеческим опытом. Этот опыт, который только и позволяет нам делать заключение о действительности, в физике принимает форму эксперимента и измерения. Мы хотим рассмотреть здесь, имея в виду квантовую механику, второй из поставленных выше вопросов.

Какой бы смысл ни вкладывался в термин «полное описание», от всякой полной теории, как нам кажется, необходимо требовать следующее: каждый элемент физической реальности должен иметь отражение в физической теории. Мы будем называть это условием полноты. Таким образом, на второй вопрос легко ответить, если мы сможем выяснить, что является элементами физической реальности.

Элементы физической реальности не могут быть определены при помощи априорных философских рассуждений; они должны быть найдены на основе результатов экспериментов и измерений. Однако для наших целей нет необходимости давать исчерпывающее определение реальности. Мы удовлетворимся следующим критерием, который считаем разумным. Если мы можем, без какого бы то ни было возмущения системы, предсказать с достоверностью (т. е. вероятностью, равной единице) значение некоторой физической величины, то существует элемент физической реальности, соответствующий этой физической величине. Нам кажется, что этот критерий, хотя он далеко не исчерпывает всех возможных способов распознавания физической реальности, по крайней мере, дает нам один из таких способов, коль скоро выполняются сформулированные в нем условия. Этот критерий, рассматриваемый не как необходимое, а только лишь как достаточное условие реальности, находится в согласии как с классическим, так и с квантово-механическим представлением о реальности.

Чтобы проиллюстрировать нашу мысль, рассмотрим квантово-механическое описание поведения частицы, имеющей одну степень свободы. Основное понятие — это понятие состояния, которое по предположению полностью характеризуется волновой функцией ψ. Последняя является функцией переменных, выбранных для описания поведения частицы. Каждой физически наблюдаемой величине А ставится в соответствие оператор, который можно обозначить той же буквой.

Если ψ есть собственная функция оператора А, т. е., если

      (1)

где а — число, то физическая величина А имеет с достоверностью значение а, коль скоро частица находится в состоянии ψ. Если ψ удовлетворяет уравнению (1), то, согласно нашему критерию реальности, для частицы в состоянии ψсуществует элемент физической реальности, соответствующий физической величине А. Пусть, например,

      (2)

где h — постоянная Планка, p₀ — некоторое постоянное число и x — независимая переменная. Так как оператор, соответствующий количеству движения частицы, имеет вид

      (3)

то мы получаем:

      (4)

Таким образом, в состоянии, которое определяется уравнением (2), количество движения имеет с достоверностью значение p₀. Значит, в этом случае имеет смысл говорить, что количество движения частицы в состоянии ψ реально.

С другой стороны, если уравнение (1) не выполняется, мы больше не можем говорить о том, что физическая величина А имеет определенное значение. Так обстоит дело, например, с координатой частицы. Оператор q, соответствующий координате, есть оператор умножения на независимую переменную. Таким образом,

      (5)

Согласно квантовой механике, мы только можем сказать, что относительная вероятность того, что измерение координаты дает результат, лежащий между a и b, равна

      (6)

Так как эта вероятность не зависит от а, а зависит только от разности b – а, мы видим, что все значения координаты равновероятны.

Итак, для частицы в состоянии ψ [формула (2)] определенного значения координаты предсказать нельзя, а его можно получить только путем непосредственного измерения. Такое измерение вызовет, однако, возмущение частицы, и, таким образом, изменит ее состояние. После того как координата будет определена, частица уже не будет больше находиться в состоянии, задаваемом формулой (2). Обычно в квантовой механике из этого делается следующий вывод: если количество движения частицы известно, то ее координата не имеет физической реальности.

В квантовой механике доказывается и более общее положение: если операторы, соответствующие двум физическим величинам, скажем А и В, не коммутируют, т. е. если AB ≠ BA, то точное знание одной из этих величин исключает точное знание другой. Кроме того, каждая попытка экспериментально определить вторую величину будет менять состояние таким образом, что уничтожит знание первой.

Из этого следует, что либо 1) квантово-механическое описание реальности посредством волновой функции неполно, либо 2) когда операторы, соответствующие двум физическим величинам, не коммутируют, эти две величины не могут одновременно быть реальными. Ибо, если бы обе они одновременно были реальными, и следовательно, имели определенные значения, то эти значения должны были бы по условию полноты содержаться в полном описании. Значит, если бы волновая функция обеспечивала полное описание реальности, то оно должно было бы включать эти значения, и их можно было бы предсказывать. Так как это не имеет места, то мы остаемся перед сформулированной выше альтернативой.

В квантовой механике обычно предполагается, что волновая функция действительно дает полное описание физической реальности для системы в состоянии, которому она соответствует. На первый взгляд это предположение вполне приемлемо, так как информация, которая может быть получена из знания волновой функции, кажется точно соответствующей той, которую можно получить при помощи измерений, не изменяя состояния системы. Мы покажем, однако, что это предположение вместе с данным выше критерием реальности приводит к противоречию.

– 2 –

Для этой цели вообразим себе, что имеются две системы I и II, которым мы даем взаимодействовать от момента времени t = 0 до t = Т, после чего между обеими частями уже не происходит больше никакого взаимодействия. Кроме того, мы предположим, что состояния обеих систем до t = 0 были известны. Мы можем тогда вычислить с помощью уравнения Шредингера состояние объединенной системы I + II во всякий последующий момент времени, в частности для любого t > Т . Обозначим соответствующую волновую функцию через Ψ. Мы не можем, однако, вычислить того состояния, в котором каждая из двух систем останется после взаимодействия. Согласно квантовой механике, это состояние может быть найдено только с помощью последующих измерений, путем процесса, известного под названием «редукции волнового пакета». Рассмотрим сущность этого процесса.

Пусть a₁, a₂, a₃,...— собственные значения некоторой физической величины А, относящейся к системе I, и u₁(x₁), u₂(x₁), u₃(x₁), ..., — соответствующие собственные функции, причем x₁ обозначает совокупность переменных, которые служат для описания первой системы. Тогда Ψ, рассматриваемая как функция от x₁ может быть выражена в виде ряда

      (7)

где x₂, обозначает переменные, которые служат для описания второй системы. Здесь величины ψ_n(x₂) должны рассматриваться просто как коэффициенты разложения Ψ(x₁, x₂) в ряд по ортогональным функциям u_n(x). Предположим теперь, что величина А измерена, причем найдено, что она имеет значение a_k. Отсюда выводят заключение, что после измерения первая система остается в состоянии, описываемом волновой функцией u_k(x₁), тогда как вторая система — в состоянии с волновой функцией u_k(x₂). Это и есть процесс редукции волнового пакета: волновой пакет, задаваемый бесконечным рядом (7), сводится к одному члену ψ_k(x₂) u_k(x₁).

Последовательность функций u_n(x₁) определяется выбором физической величины А. Если вместо нее мы выбрали бы другую величину, скажем В, имеющую собственные значения b₁, b₂, b₃,... и собственные функции v₁(x₁), v₂(x₁), v₃(x₁), ..., мы бы получили вместо соотношения (7) разложение

      (8)

где величины φ_s(x₂) представляют собой новые коэффициенты. Если теперь измеряется величина В, причем она оказывается равной b_r , то мы заключаем, что после измерения первая система остается в состоянии, которое описывается функцией v_r(x₁), а вторая система остается в состоянии, которое описывается функцией φ_r(x₂).

Мы видим поэтому, что в результате двух различных измерений, произведенных над первой системой, вторая система может оказаться в двух разных состояниях, описываемых различными волновыми функциями. С другой стороны, так как во время измерения эти две системы уже не взаимодействуют, то в результате каких бы то ни было операций над первой системой во второй системе уже не может получиться никаких реальных изменений. Это, конечно, является лишь другой формулировкой того, что понимается под отсутствием взаимодействия между двумя системами. Таким образом, одной и той же реальности (вторая система после взаимодействия с первой) можно сопоставить две различные функции (в нашем примере ψ_k и φ_r ).

Но ведь может случиться, что две волновые функции ψ_k и φ_r являются собственными функциями двух некоммутирующих операторов, соответствующих некоторым физическим величинам Р и Q. Что такой случай действительно возможен, лучше всего можно показать на примере. Предположим, что две системы являются двумя частицами и что функция Ψ(x₁, x₂) равна

      (9)

где x₀ — некоторая константа. Пусть величиной А будет количество движения первой частицы; тогда, как мы знаем из уравнения (4), ее собственные функции, соответствующие собственному значению р, будут

      (10)

Так как мы имеем здесь случай сплошного спектра, уравнение (7) перепишется в виде

      (11)

где

      (12)

Но это ψ_p является собственной функцией оператора

      (13)

соответствующей собственному значению — p второй частицы. С другой стороны, если величина B первой частицы, то ее собственной функцией, соответствующей собственному значению x, будет

      (14)

где δ(x₁ – x) — есть хорошо известная дельта-функция Дирака. Уравнение (8) в этом случае примет вид

      (15)

где

      (16)

Но φ_x является собственной функцией оператора

      (17)

соответствующей собственному значению x + x₀ координаты второй частицы. Так как

      (18)

то мы показали, что, вообще говоря, возможен случай, когда ψ_k и φ_r являются собственными функциями двух некоммутирующих операторов, соответствующих двум физическим величинам.

Вернемся теперь к общему случаю, к которому относятся соотношения (7) и (8). Мы предположим, что ψ_k и φ_r действительно являются собственными функциями некоторых некоммутирующих операторов Р и Q, причем ψ_k соответствует собственному значению p_k, а φ_r соответствует собственному значению q_r. В таком случае, измерив А и В, мы сможем предсказать с достоверностью и без какого бы то ни было возмущения второй системы либо значение величины Р (т. е. p_k ), либо значение величины Q (т. е. q_r ). Согласно нашему критерию реальности, в первом случае мы должны считать элементом реальности величину Р, а во втором случав элементом реальности будет величина Q. Но, как мы видели, обе волновые функции ψ_k и φ_r относятся к одной и той же реальности.

Выше мы показали, что или 1) квантово-механическое описание реальности посредством волновой функции не является полным или 2) если операторы, соответствующие двум физическим величинам, не коммутируют, эти две величины не могут одновременно обладать реальностью. Исходя затем из предположения, что волновая функция действительно дает полное описание физической реальности, мы пришли к выводу, что две физические величины с некоммутирующими операторами могут быть реальными одновременно. Таким образом, отрицание «1» приводит к отрицанию единственного остающегося предположения «2». Итак, мы вынуждены заключить, что квантово-механическое описание физической реальности посредством волновых функций не является полным.

На это заключение можно было бы возражать, основываясь на том, что наш критерий реальности не является достаточно ограничивающим. Действительно, мы бы не пришли к нашему заключению, если бы настаивали на том, что две или больше физических величины могут одновременно считаться элементами реальности только в том случае, если их можно одновременно измерить или предсказать. С этой точки зрения величины Р и Q одновременно не обладают реальностью, поскольку предсказать можно либо Р, либо Q, но не Р и Q одновременно. Здесь реальность Р и Q ставится в зависимость от процесса измерения, производимого над первой системой, хотя этот процесс никоим образом не влияет на вторую систему. Никакое разумное определение реальности не должно, казалось бы, допускать этого.

Хотя мы и показали, что волновая функция не дает полного описания физической реальности, мы оставили открытым вопрос о том, существует ли такое описание или нет. Мы думаем, однако, что такая теория возможна.

Теория квантов и основы физики

А. Эйнштейн, 1936 г., СНТ, т. 4, с. 218 – 224.
Пятый параграф из работы "Физика и реальность"

Физики-теоретики нашего поколения ожидают, что для физики будет построена новая теоретическая основа, которая воспользуется фундаментальными представлениями, значительно отличающимися от представлений рассмотренной до сих пор теории поля. Основанием для этого служит признание необходимости использования новых методов исследования при математическом представлении явлений, получивших название квантовых.

Тогда как недостатки классической механики, выявленные теорией относительности, связаны с конечностью скорости света (исключается ее бесконечность), в начале нашего века было обнаружено, что между выводами механики и результатами опыта существуют другие противоречия, которые связаны с конечным значением (исключается равенство нулю) постоянной Планка h. В частности, молекулярная механика требует, чтобы теплоемкость и плотность излучения (монохроматического) твердых тел убывали пропорционально уменьшению их абсолютной температуры; опыт показал, что эти величины убывают быстрее абсолютной температуры. Для теоретического объяснения их поведения необходимо предполагать, что энергия механической системы может принимать не любые, а только определенные дискретные значения, математическое выражение которых всегда зависит от постоянной Планка h. Больше того, эта концепция была существенно важной для теории атома (теория Бора). Для перехода атомов из одного состояния в другое — с излучением или поглощением и без них — нельзя было указать никакого каузального закона, а только статистический; к такому же заключению пришли и для радиоактивного распада атомов, который тоже тщательно изучался в эту эпоху. Более двух десятилетий физики безуспешно пытались найти единую интерпретацию этого «квантового характера» определенных групп явлений. Такая попытка увенчалась успехом около 10 лет назад путем использования двух совершенно различных теоретических методов. Одним из этих методов мы обязаны Гейзенбергу и Дираку, другим—Луи де Бройлю и Шредингеру. Математическая эквивалентность обоих методов была вскоре доказана Шредингером. Хочу попытаться наметить ход мыслей Луи де Бройля и Шредингера, который ближе к способу мышления физиков, затем изложить некоторые общие соображения.

Вначале вопрос ставится так: каким образом можно определить для системы дискретный ряд значений энергии Н_σ , определяемой в смысле классической механики (энергия является заданной функцией координат q_r и соответствующих количеств движения p_r )? Константа Планка h связывает частоту Н_σ / h со значениями энергии Н_σ . Итак, достаточно считать, что система имеет дискретный ряд значений частоты. Это напоминает нам, что в акустике ряд дискретных значений частоты соответствует линейному уравнению в частных производных (если граничные условия заданы), т. е. периодическим синусоидальным решениям. Аналогичным способом Шредингер поставил себе задачу сопоставить заданной функции энергии ε (q_r , p_r ) уравнение в частных производных для некоторой скалярной функции ψ, где q_r , и время t являются независимыми переменными. Ему это удалось (для комплексной функции-ψ) в том смысле, что теоретические значения энергии Н_σ , указанные статистической теорией, действительно вытекают удовлетворительным образом из периодического решения уравнения.

Само собой разумеется, что было невозможно сопоставить определенному решению ψ (q_r , t) уравнения Шредингера определенное движение материальных точек в механическом смысле. Это означает, что функция ψ не определяет, по крайней мере точно, историю q_r как функции времени. Однако, следуя Борну, физическое значение функций ψ можно интерпретировать следующим образом: ψψ* (квадрат абсолютного значения комплексной функции ψ) является плотностью вероятности конфигураций q_r в момент t в рассматриваемой точке конфигурационного пространства. Следовательно, содержание уравнения Шредингера можно характеризовать следующим, легко понимаемым, но не совсем точным образом: оно определяет изменение во времени плотности вероятности статистического ансамбля систем в пространстве конфигураций. Короче говоря, уравнение Шредингера определяет изменение во времени функции ψ от q_r .

Необходимо отметить, что результаты этой теории содержат результаты механики точки как предельные значения, когда длина волны, с которой встречаются при решении задачи Шредингера, повсюду столь мала, что потенциальная энергия меняется практически бесконечно мало при изменениях порядка одной длины волны в конфигурационном пространстве. При этих условиях ясно выделяется следующее: выберем в конфигурационном пространстве область G₀ , большую (по всем размерам) относительно длины волны, но малую по сравнению с практическими размерами конфигурационного пространства. При этих условиях возможно выбрать функцию ψ так, что для начального момента t₀ она исчезает вне области G₀ и ведет себя, в соответствии с уравнением Шредингера, таким же образом, по крайней мере приближенно, и для последующего времени, но относительно области, которая к этому времени t перешла в другую область G. Тогда можно будет с определенной степенью приближения говорить о движении области G в целом и заменить это движение движением точки в конфигурационном пространстве. Это движение совпадает с требуемыми уравнениями классической механики.

Опыты по интерференции корпускулярных лучей дали блестящее подтверждение того, что предполагаемый теорией волновой характер явлений движения действительно соответствует фактам. Кроме того, в теории легко удалось вывести статистические законы перехода системы из одного квантового состояния в другое под действием внешних сил, что, с точки зрения классической механики, казалось чудом. Внешние силы здесь представлены небольшими, зависящими от времени приращениями потенциальной энергии. Тогда как в классической механике такие приращения могут вызвать только соответственно малые изменения в системе, в квантовой механике они же вызывают изменения любой величины, но с соответственно малой вероятностью; это следствие полностью соответствует опыту. Теория даже позволила понять, по крайней мере в основных чертах, законы радиоактивного распада.

Очевидно в прошлом никогда не была развита теория, которая, подобно квантовой, дала бы ключ к интерпретации и расчету группы столь разнообразных явлений. Несмотря на это, я все-таки думаю, что в наших поисках единого фундамента физики эта теория может привести нас к ошибке: она дает, по-моему, неполное представление о реальности, хотя и является единственной, которую можно построить на основе фундаментальных понятий силы и материальных точек (квантовые поправки к классической механике). Неполнота представления является результатом статистической природы (неполноты) законов. Я хочу сейчас обосновать это мнение.

Я спрашиваю сначала — до какой степени функция ψ описывает реальное состояние механической системы? Допустим, что ψ_r — периодические решения уравнения Шредингера (расположенные в порядке возрастания значений энергии). Я оставляю пока в стороне вопрос о том, в какой степени отдельные ψ_r дают полное описание физических состояний. Вначале система находится в состоянии ψ₁ с наименьшей энергией ε₁ . Затем в течение конечного промежутка времени на систему действует небольшая возмущающая сила. Для некоторого последующего момента из уравнения Шредингера получаем функцию ψ в виде:

где C_r — постоянные (комплексные). Если ψ_r «нормированы», то C₁ почти равен единице, C₂ и т. д. малы по сравнению с единицей. Можно теперь спросить: описывает ли ψ действительное состояние системы? Если ответ положительный, то единственное, что нам остается,— это приписать этому состоянию определенную энергию E. [Потому что, согласно прочно установленному следствию теории относительности, энергия системы (в покое) равна ее массе (как целого). А последняя должна иметь вполне определенное значение.] А именно: такую E, которая не намного превосходит E₁ (во всяком случае E₁ < E < E₂ ). Но такое предположение противоречит опытам Франка и Герца по соударению электронов, если к этому же принято данное Милликеном доказательство дискретной природы электричества.

В действительности, эти опыты приводят к заключению, что между двумя квантовыми значениями не существует никаких других значений энергии. Отсюда следует, что наша функция ψ никоим образом не описывает состояние самой системы, а скорее представляет собой статистическое описание, при котором C_r выражают вероятности отдельных значений энергии. Следовательно, кажется очевидным, что данное Борном статистическое истолкование квантовой теории является единственно возможным. Функция ни в коем случае не описывает состояние, свойственное одной единственной системе; она относится скорее к нескольким системам, т. е. к «ансамблю систем», в смысле статистической механики. Если, исключая некоторые особые случаи, функция дает только статистические данные об измеримых величинах, то причина состоит не только в том, что операция измерения вносит неизвестные элементы, которые можно уловить лишь статистически, а в самом факте, что функция ψ ни в коем смысле не описывает состояния одной отдельной системы.

Такая интерпретация устраняет также и указанный недавно мною и моими двумя сотрудниками парадокс, относящийся к следующей проблеме.

Рассмотрим механическую систему, состоящую из двух отдельных систем А и В, взаимодействующих только в течение ограниченного времени. Пусть задана функция ψ до взаимодействия. Тогда уравнение Шредингера даст функцию ψ после взаимодействия. Определим теперь физическое состояние подсистемы А настолько полно, насколько это допускается измерениями. Тогда квантовая механика позволяет нам определить функцию ψ для подсистемы В по сделанным измерениям и функции ψ для всей системы. Это определение, однако, дает результат, который зависит от того, какие определяющие величины, характеризующие состояние А, измерялись (например, координаты или количества движения). Поскольку после взаимодействия для В может существовать только одно физическое состояние, которое нельзя себе разумно представить зависящим от отдельных измерений, произведенных над системой А, отделенной от В, можно заключить, что функции ψ нельзя однозначно сопоставить физическое состояние. Это сопоставление нескольких функций ψ одному и тому же физическому состоянию системы В вновь показывает, что функция не может интерпретироваться как описание (полное) физического состояния одной отдельной системы. Здесь также все трудности исчезают, если функция ψ сопоставляется с ансамблем систем [Операция измерения А, например, также содержит в себе переход к более ограниченному ансамблю систем. Последний (а значит, и его ψ-функция) зависит оттого, с какой точки зрения было произведено ограничение ансамбля систем].

Тот факт, что квантовая механика позволяет столь просто получить выводы, касающиеся прерывных переходов (кажущихся) из одного состояния системы в другое, не давая фактически представления об отдельных процессах, связан с другим фактом, а именно: что теория в действительности оперирует не с отдельной системой, а с ансамблем систем. Коэффициенты C_r в нашем первом примере очень мало меняются под действием внешних сил. Такая интерпретация квантовой механики позволяет понять, почему эта теория так легко объясняет способность малых возмущающих сил вызывать изменения любой величины в физическом состоянии системы. Такие возмущающие силы вызывают фактически лишь соответствующие малые изменения статистической плотности ансамбля систем, а следовательно, бесконечно малые изменения функции ψ; математическое выражение этих изменений представляет гораздо меньше трудностей, чем представляло математическое выражение конечных изменений, претерпеваемых отдельными системами. Что происходит в отдельной системе, остается, правда, при такой манере мышления совершенно невыясненным; статистическая точка зрения совершенно исключает из рассмотрения эти таинственные процессы.

Но теперь я спрашиваю: неужели какой-нибудь физик действительно верит, что нам не удастся узнать что-либо о важных внутренних изменениях в отдельных системах, об их структуре и причинных связях? И это несмотря на возникшие благодаря замечательным открытиям камеры Вильсона и счетчика Гейгера возможности исследования? Думать так логически допустимо, но это настолько противоречит моему научному инстинкту, что я не могу отказаться от поисков более полной концепции.

К этому мы хотели бы добавить некоторые соображения иного рода, которые также свидетельствуют против идеи, что введенные квантовой механикой методы способны создать основу, пригодную для всей физики. В уравнении Шредингера абсолютное время и потенциальная энергия играют решающую роль, тогда как теорией относительности эти два понятия признаны в принципе недопустимыми. Чтобы избежать этих трудностей, нужно основать теорию на понятии поля и законах полей, а не на силах взаимодействия. Это приводит к распространению статистических методов квантовой механики на поля, т. е. на системы с бесконечным числом степеней свободы. Хотя во всех сделанных до сих пор попытках ограничивались линейными уравнениями, которые, как мы знаем по данным общей теории относительности, недостаточны, встретившиеся при осуществлении уже этих весьма остроумных попыток осложнения ужасающе велики. Они возрастают чрезвычайно, если мы хотим удовлетворить требованиям общей теории относительности, правомочность которой в принципе никем не может оспариваться.

Необходимо отметить, конечно, что введение пространственно-временного континуума может считаться противоестественным, если иметь в виду молекулярную структуру всего происходящего в микромире. Утверждают, что успех метода Гейзенберга может быть приведен к чисто алгебраическому методу описания природы, т. е. исключению из физики непрерывных функций. Но тогда нужно будет в принципе отказаться от пространственно-временного континуума. Можно думать, что человеческая изобретательность в конце концов найдет методы, которые позволят следовать этому пути. Но в настоящее время такая программа смахивает на попытку дышать в безвоздушном пространстве.

Нет сомнения, что в квантовой механике имеется значительный элемент истины и что она станет пробным камнем для любой будущей теоретической основы, из которой она должна будет быть выведена как частный случай, подобно тому, как электростатика выводится из уравнений Максвелла для электромагнитного поля или термодинамика из классической механики. Однако я не думаю, что квантовая механика является исходной точкой поисков этой основы, точно так же, как нельзя, исходя из термодинамики (или, соответственно, из статистической механики), прийти к основам механики.

Учитывая такое положение, кажется вполне оправданным серьезное рассмотрение вопроса о том, нельзя ли каким-нибудь образом привести в соответствие основу физики поля с данными квантовой теории? Не является ли она единственной основой, которая, в соответствии с современными возможностями математики, может быть адаптирована к требованиям общей теории относительности? Господствующая среди современных физиков вера в совершенную безнадежность таких попыток коренится в необоснованном мнении, что в первом приближении такая теория должна привести к уравнениям классической механики для движения частиц или по крайней мере к обыкновенным дифференциальным уравнениям. Фактически до настоящего времени нам ни разу не удалось теоретически представить частицы с помощью полей, свободных от сингулярностей, и мы не можем ничего a priori сказать по поводу поведения таких сущностей. Однако одно достоверно: если теории поля удастся представить частицы без сингулярностей, то поведение этих частиц во времени будет однозначно определяться дифференциальными уравнениями поля.

Квантовая механика и действительность

А. Эйнштейн, 1948 г., СНТ, т. 3, с. 612 – 616.

В этой статье я хочу кратко и элементарно изложить, почему я не считаю метод квантовой механики в принципе удовлетворительным. Однако в то же время я хочу заметить, что никоим образом не собираюсь отрицать того, что эта теория представляет выдающийся, в известном смысле даже окончательный, шаг в физическом познании. Мне представляется, что эта теория будет содержаться в более поздней примерно так, как геометрическая оптика в волновой оптике: связи останутся, но основа будет развита и, соответственно, заменена более широкой.

– I –

Свободную частицу в некоторый момент времени я представляю себе описываемой (полно в смысле квантовой механики) пространственно ограниченной ψ-функпией. Согласно такому представлению, частица не имеет ни точно определенного количества движения (импульса), ни точно определенного положения в пространстве.

В каком смысле должен я теперь представлять себе то, что это описание отражает действительно конкретное положение дел? Мне представляются возможными два близких понимания, которые мы и сопоставим:

а) В действительности (свободная) частица имеет определенное положение в пространстве и определенный импульс, если даже они в том же индивидуальном случае не могут быть одновременно установлены путем измерения. Согласно этому толкованию, ψ-функция дает неполное описание реального положения вещей.

Это толкование не является общепринятым у физиков. Его принятие привело бы к тому, что от физики потребовалось бы дать, наряду с неполным, полное описание положения вещей и найти законы такого описания. Этим были бы подорваны теоретические рамки квантовой механики.

б) Частица не имеет в действительности ни определенного импульса ни определенного положения в пространстве; описание с помощью ψ-функции является в принципе полным описанием. Точное местоположение частицы, которое я получаю в результате его измерения, не может быть интерпретировано как местоположение частицы до измерения. Точная локализация, которая обнаруживается при измерении, будет проявляться только через неизбежное (не несущественное) воздействие измерения. Результат измерения зависит не только от реального положения частицы, но также и от принципиально неполного знания природы механизма измерения. Аналогично обстоит дело и в том случае, когда измеряется импульс или некоторая другая относящаяся к частице наблюдаемая величина. Это, пожалуй, наиболее предпочтительная у физиков современная интерпретация; следует признать, что в рамках квантовой механики только она естественным образом согласуется с эмпирическими фактами, выраженными в принципе неопределенности Гейзенберга.

Согласно этому толкованию, две различные (не только тривиально) ψ-функции описывают всегда две различные реальные ситуации (например, частицы с точно определенным положением в пространстве и, соответственно, частицы с точно определенным импульсом).

Сказанное справедливо, с необходимыми изменениями, также и для описания систем, состоящих из многих материальных точек. Здесь мы признаем также (в смысле интерпретации 1"б"), что ψ-функция полностью описывает реальное положение вещей и что две (существенно) различные функции описывают две различные ситуации и тогда, когда они при проведении полного измерения приводят к совпадающим результатам; в этом случае совпадение результатов измерения будет отчасти приписано не полностью известному влиянию измерительного устройства.

– II –

Если спросить, что характерно для мира физических идей, независимо от квантовой теории, то прежде всего бросается в глаза следующее: понятия физики относятся к реальному внешнему миру, т.е. они предполагают идеи о вещах, требующих независимого от воспринимающих субъектов «реального существования» (тела, поля и т.д.); эти идеи, с другой стороны, приводятся в возможно более верное соответствие с чувственными восприятиями. Характерным для этих физических объектов является, далее, то что они мыслятся распределенными некоторым образом в пространственно-временном континууме. Существенным для этого распределения вводимых в физику объектов является требование существования вещей в некоторый определенный момент времени независимо друг от друга, поскольку они «находятся в различных частях пространства». Без признания такой независимости существования («бытия как такового») пространственно отдаленных друг от друга объектов, которое берет свое начало от обыденного мышления, было бы невозможно физическое мышление в привычном для нас смысле. Без такого чистого обособления было бы неясно также, как могли формулироваться и проверяться физические законы. Теория поля довела этот принцип до крайности, локализовав в (четырехмерных) бесконечно малых пространственных элементах лежащие в ее основе независимо друг от друга существующие объекты, а также постулированные для них элементарные законы.

Для относительной независимости пространственно отдаленных объектов (А и В) характерна следующая идея: внешнее влияние А не имеет никакого непосредственного влияния на В; это известно как «принцип близкодействия», который последовательно применяется только в теории поля. Полное упразднение этого основного положения сделало бы невозможной идею о существовании (квази-) замкнутых систем и вместе с тем установление эмпирически проверяемых законов в привычном для нас смысле.

– III –

Я утверждаю, что квантовая механика в ее интерпретации (1 "б") не совместима с основным положением II.

Рассмотрим физическую систему S₁₂, которая состоит из двух подсистем: S₁и S₂. Обе эти подсистемы в прошлом могли находиться в физическом взаимодействии. Но мы рассматриваем их в момент времени t, когда это взаимодействие уже отсутствует. Вся система описывается полностью (в смысле квантовой механики) ψ-функцией ψ₁₂ с координатами q₁,..., и, соответственно, q₂,..., обоих подсистем [ψ₁₂ будет представляться не как произведение вида ψ(q₁,...) ψ(q₂,...), но только как сумма таких произведений]. В момент времени t обе подсистемы пространственно разделены друг от друга настолько, что ψ₁₂ только тогда отлично от 0, когда q₁,... принадлежит ограниченной пространственной области R₁ и q₂,...— отделенной от R₁ пространственной области R₂.

В этом случае ψ-функции отдельных подсистем S₁и S₂ прежде всего неизвестны и вообще не существуют. Но методы квантовой механики позволяют определить ψ₂ системы S₂ из ψ₁₂, если к тому же имеется в смысле квантовой механики полное измерение подсистемы S₁. Из определенной таким образом первоначальной функции ψ₁₂, системы S₁₂ получают ψ-функцию ψ₂, подсистемы S₂.

В этом определении, однако, имеет существенное значение то, какого рода полное (в квантово-механическом смысле) измерение подсистемы S₁ предпринимается, т. е. какую наблюдаемую мы измеряем. Если, например, S₁ — одна-единственная частица, то нам позволяется измерить ее координаты, или компоненты ее импульса. Сообразно этому выбору мы получаем для ψ₂ другого рода представление, а именно такое, при котором в зависимости от выбора измерения системы S₁ следуют различного рода (статистические) предсказывания о дополнительных предпринимаемых измерениях в S₂. С точки зрения интерпретации 1"б", это означает, что сообразно выбору полного измерения в S₁ создаются относительно S₂ различные реальные ситуации, которые описываются разного рода ψ₂, ψ'₂, ψ''₂ и т.д.

С точки зрения только квантовой механики это не представляет никакой трудности. Сообразно особому выбору измерения в S₁ создается именно различная реальная ситуация, и нет необходимости поступать так, чтобы в той же самой системе S₂ одновременно сопоставлялись две или больше различные ψ-функции ψ₂, ψ'₂,...

Однако иначе обстоит дело в том случае, когда пытаются одновременно с принципами квантовой механики придерживаться принципа II о самостоятельном существовании имеющегося в двух разобщенных частях пространства R₁ и R₂ реального положения вещей. В нашем примере именно полное измерение в S₁ означает физическое вмешательство, которое касается только пространства R₂. Но такое вмешательство не может непосредственно оказать влияние на физическую реальность в отдаленной части пространства R₂. Из этого следовало бы, что каждое высказывание относительно S₂, которое мы могли бы получить на основе полного измерения в S₁ для системы S₂ должно было бы иметь значение также тогда, когда вообще никакого измерения в S₁ не производилось. Это означало бы, что для S₂ должны были бы быть справедливыми одновременно все высказывания, которые можно было бы вывести из положения о ψ₂,... или ψ'₂,.... Это, конечно, невозможно, когда ψ₂, ψ'₂,... означают отличное друг от друга реальное положение вещей в S₂, т. е. когда вступают в конфликт с интерпретацией I"б" ψ-функции.

Мне кажется, не подлежит сомнению, что физики, которые считают квантово-механический способ описания принципиально окончательным, будут на эти соображения реагировать следующим образом: они откажутся от требования II о независимом существовании имеющихся в различных областях пространства физических реальностей; они могут с полным правом ссылаться на то, что квантовая теория явно нигде не применяет это требование.

Я соглашаюсь с этим, но хочу заметить, что, когда я рассматриваю известные мне физические явления и, в особенности, те их них, которые так успешно изучаются с помощью квантовой механики, то я все же нигде не нахожу факта, который казался бы мне достаточно основательным, чтобы отказаться от требования II. Поэтому я склонен думать, что следовало бы рассматривать описание квантовой механики в смысле 1"а"как неполное и непрямое описание реальности, которое позже будет заменено опять полным и прямым.

Во всяком случае нужно, по моему мнению, остерегаться того, чтобы при отыскании единой основы для всей физики догматически опираться на схему современной теории.

Элементарные соображения по поводу
интерпретации основ квантовой механики

А. Эйнштейн, 1953 г., СНТ, т. 3, с. 617 – 622.

Своеобразие современной ситуации в квантовой механике состоит, по-моему, в том, что сомнениям подвергается не математический аппарат теории, а физическая интерпретация ее утверждений. Каково отношение ψ-функции к конкретной единичной ситуации, т. е. к индивидуальному состоянию некоторой отдельно взятой системы? Иными словами: что говорит ψ-функция об (индивидуальном) «реальном состоянии»?

Прежде всего можно усомниться в том, что такой вопрос вообще имеет какой-либо смысл. Действительно, можно встать на такую точку зрения: «реальное» есть только результат отдельного наблюдения, а не то, что объективно существует в пространстве и времени независимо от акта наблюдения. Принимая эту чисто позитивистскую точку зрения, можно, очевидно, не думать о том, как понимать «реальное состояние» в рамках квантовой теории. Тогда попытки ответить на поставленный вопрос напоминают борьбу с призраками.

Но эта чисто позитивистская точка зрения — если ее проводить последовательно — имеет один непоправимый недостаток: она ведет к тому, что следует считать лишенными смысла вообще все словесные высказывания. Вправе ли мы говорить, что описание отдельного результата наблюдений имеет смысл и, соответственно, что оно истинно или ложно? Разве не может такое описание основываться на обмане чувств или на ощущениях, которые можно было бы истолковать как воспоминания о сновидениях или как галлюцинации? Имеет ли вообще какой-либо объективный смысл различие между ощущениями наяву и во сне? В конце концов, «реальными» остаются только ощущения некоего «я» без какой-либо возможности что-нибудь сказать о них. В самом деле, понятия, применяемые в высказываниях, при чисто позитивистском анализе все без исключений оказываются лишенными смысла.

В действительности же применяемые в наших высказываниях независимые понятия и системы понятий являются творением человека, созданными им орудиями, оправдание и ценность которых основываются исключительно на том, что они позволяют «с пользой» упорядочить ощущения (оправданность). Иначе говоря, применение этих орудий оправдано, поскольку понятия позволяют «объяснить» ощущения.

[В основе словесного родства слов «правда» и «оправдываться» лежит родство по существу; не следует понимать это утверждение только в утилитарном смысле.]

Только с точки зрения этой оправданности и следует выносить суждение об обоснованности понятий и систем понятий. Это относится также и к понятиям «физическая реальность», «реальность внешнего мира», «реальное состояние системы». Априори нет оснований считать эти понятия логически необходимыми или запрещать их; это решает только оправданность. За этими словами-символами кроется целая программа, которая безусловно служила основой развития физического мышления вплоть до создания квантовой теории: все должно сводиться к мысленным пространственно-временным объектам и к закономерным связям между этими объектами. В таком описании нет ничего, что было бы связано с эмпирическими знаниями об этих объектах. Например, Луне в каждый данный момент времени приписывается положение в пространстве (относительно некоторой системы координат), независимо от того, наблюдается это положение или нет. Этот способ описания и подразумевают, когда говорят о физическом описании «реального внешнего мира», каким бы ни был выбор элементарных понятий (материальные точки, поле и т. д.), положенных в основу такого описания.

Физики не подвергали серьезным сомнениям обоснованность этой программы, пока казалось, что все фигурирующие при таком описании понятия в принципе можно установить эмпирически в каждом отдельном случае. Иллюзорность подобных представлений убедительно показал Гейзенберг на примере квантовых явлений.

После его работ понятие «физической реальности» стало проблематичным и возник вопрос, что же собственно пытается описывать теоретическая физика (с помощью квантовой механики) и к чему относятся открываемые ею закономерности. На этот вопрос отвечают по-разному.

Чтобы подойти к ответу на этот вопрос, посмотрим, что говорит квантовая механика о макросистемах, т. е. о таких объектах, которые мы можем «воспринимать непосредственно». Мы знаем, что такие объекты и законы, управляющие ими, описываются классической физикой с большой, хотя и не сколь угодно высокой, точностью. Мы не сомневаемся, что такие объекты в каждый момент времени занимают некоторое реальное положение (место) и обладают некоторой скоростью (импульсом), т. е. они находятся в некотором реальном состоянии (все это в приближении обусловленном квантовой структурой).

Спросим теперь: включает ли в себе квантовая механика (с вытекающими из нее ограничениями на точность) то реальное описание движения макроскопических тел, которое дает классическая механика? Если же на этот вопрос нельзя просто ответить «да», то в каком смысле об этом можно говорить? Чтобы ответить на этот вопрос, рассмотрим следующий конкретный пример.

Специальный пример

Рассмотрим систему, состоящую из шарика диаметром около 1 мм, который движется вперед и назад (вдоль оси X некоторой системы координат) между двумя параллельными стенками (расстояние между которыми составляет примерно 1 м). Пусть столкновения шарика со стенками будут идеально упругими. Теперь будем описывать стенки в этой идеализированной макроскопической системе круто возрастающим потенциалом, выражение для которого зависит только от координат материальных точек, образующих шарик. Пусть нам удалось сделать так, что в процессе отражения не устанавливается никакой связи между координатой центра тяжести шарика х и его «внутренними» координатами (включая угловые). Этим мы достигаем того, что для наших целей положение шарика (с точностью до его радиуса) может описываться одной координатой х.

С точки зрения квантовой механики здесь речь идет о процессе с точно заданной энергией. Тогда волна де Бройля (ψ-функция) будет гармонической по времени. Кроме того, она будет отлична от нуля только между х = –l/2 и х = +l/2. Вне этого отрезка ψ-функция равна нулю. Вследствие же непрерывности ψ-функции она должна обращаться в нуль в концевых точках отрезка, т. е. при х = ±l/2.

Следовательно, ψ-функция является стоячей волной, которую можно представить на этом отрезке в виде суперпозиции двух гармонических волн, распространяющихся в противоположных направлениях:

      (1)

или

      (1a)

Из равенства (1а) легко видеть, что множитель А в обоих равенствах должен быть одинаковым, если мы хотим удовлетворить граничным условиям на концах отрезка. Не ограничивая общности, множитель А можно, взять вещественным. Согласно уравнению Шредингера, величина b полностью определяется массой m. Будем считать, что множитель А нормирован обычным способом.

Для правомерности сравнения этого примера с соответствующей задачей классической механики мы должны еще предположить, что длина волны де Бройля 2π/b мала по сравнению с l.

Прежде всего, примем, как обычно, вероятностную интерпретацию ψ-функции, предложенную Борном:

Это — вероятность того, что координата х центра тяжести шарика лежит в заданном интервале Δх. Она равна просто const. Δх — отвлекаясь от волновой «тонкой структуры», физическая реальность которой несомненна.

Как обстоит теперь дело с вероятностью значений импульса (скорости) шарика? Эту вероятность можно наитие помощью преобразования Фурье волновой функции ψ. Если бы формула (1) была справедлива при всех x. от –∞ до +∞, то она и была бы искомым рядом Фурье. Тогда импульс имел бы два равных по абсолютной величине, но противоположных по знаку определенных значения, обладающих равной вероятностью. Поскольку же оба цуга волн ограничены, каждый из них дает интеграл Фурье с тем более узким спектральным интервалом, чем большее число волн де Бройля укладывается на длине l.. Это происходит потому, что для импульса возможны только два почти в точности равных по величине, но противоположных по знаку значения — согласующихся при этом со значениями в классическом случае,— и притом с одинаковой вероятностью.

Таким образом, с точностью до малых отклонений, обусловленных квантовой структурой, эти два статистических результата и есть то, что удовлетворяет «временному ансамблю» в случае классической теории. Следовательно, в этом отношении теория вполне удовлетворительна.

Но теперь возникает вопрос: может ли эта теория дать реальное описание отдельного события? На этот вопрос следует ответить: «нет». При этом существенно, что здесь речь идет о «макросистеме». Действительно, в случае макросистемы мы уверены, что она в каждый момент времени находится в «реальном состоянии», правильно (приближенно) описываемом классической механикой. Следовательно, отдельная макросистема рассматриваемого нами типа в каждый момент времени имеет почти определенную координату центра тяжести и — по крайней мере, усредненный по малому промежутку времени — почти определенный импульс (имеющий также определенный знак). Ни одно из этих двух значений нельзя получить из ψ-функции (1). Из нее можно получить (с помощью статистической интерпретации Борна) только такие результаты, которые относятся к статистическому ансамблю систем рассматриваемого типа.

То обстоятельство, что для рассматриваемой системы не всякая ψ-функция, удовлетворяющая уравнению Шредингера, приближенно соответствует реальному описанию в смысле классической механики, особенно четко проявляется при рассмотрении ψ-функции, являющейся суперпозицией двух решений типа (1) с частотами (или энергиями), существенно отличающимися друг от друга. В самом деле, такой суперпозиции вообще не соответствует ни один реальный случай в классической механике (она соответствует статистическому ансамблю таких реальных случаев в духе интерпретации Борна).

Обобщая сказанное, мы приходим к выводу: квантовая механика описывает ансамбль систем, но не отдельные системы. В этом смысле описание отдельной системы с помощью ψ-функции является неполным; ψ-функция не описывает реальное состояние такой системы.

Примечание. Против этого заключения можно возразить следующим образом. Рассмотренный нами случай строгой монохроматичности ψ-функции является предельным, и для него требование соответствия с задачей классической механики, возможно, окажется в виде исключения неправильным. Если взять конечный, хотя и малый интервал частот, то при соответствующем выборе амплитуд и фаз ψ-функций, участвующих в суперпозиции, можно получить ψ-функцию, которая будет приблизительно соответствовать определенной координате и определенному импульсу. Почему бы не попытаться рассматривать только такие ψ-функции и считать, что разрешенные ψ-функции описывают отдельные системы?

Такую возможность следует отвергнуть уже по той причине, что определенные значения координат в таком описании можно сохранить не для любых значений времени.

То обстоятельство, что уравнение Шредингера вместе с интерпретацией Борна не приводит к описанию реальных состояний отдельных систем, пробуждает, естественно, стремление к поискам теории, свободной от этого ограничения.

Пока в этом направлении были предприняты две попытки, причем обе основывались на использовании уравнения Шредингера и отказе от интерпретации Борна. Первая попытка восходит к де Бройлю; недавно ее с большим остроумием развивал Бом.

Подобно тому, как в своем первоначальном исследовании Шредингер пришел к волновому уравнению из рассмотрения аналогии с классической механикой (линеаризация уравнения Якоби аналитической механики), при выводе уравнения движения отдельной квантовой системы, описываемой решением уравнения Шредингера, следует исходить из той же аналогии. Правило заключается в следующем. Волновая функция ψ приводится к виду

Так из ψ получаются две (вещественные) функции координат, R и S. Тогда, дифференцируя R по координатам, можно найти импульсы, или скорости, системы как функции времени, если координаты рассматриваемой отдельной системы в некоторый момент времени заданы.

Равенство (1а) показывает, что в нашем случае ∂S/∂х, а значит и скорость, тождественно равны нулю. Такое возражение против этой теоретической попытки, выдвинутое, впрочем, еще четверть века назад Паули, применительно к нашему примеру является особенно веским. Обращение скорости в нуль противоречит разумному требованию, что в случае макросистемы движение приближенно должно соответствовать классической механике.

Вторая попытка прийти к описанию реального состояния отдельной системы на основе уравнения Шредингера недавно была предпринята самим Шредингером. Его идея, если говорить коротко, заключается в следующем. Функция ψ сама является реальностью и не нуждается в интерпретации Борна. Атомистических образований, о которых до сих пор должно было что-то говорить ψ-поле, не существует вообще, по крайней мере как локализованных объектов. В применении к нашей макросистеме это означает: макроскопическое тело, как таковое, не существует вообще; во всяком случае не существует — хотя бы приближенно — таких вещей, как положение его центра тяжести в данный момент времени. Следовательно, здесь также нарушается требование, чтобы квантово-механическое описание движения макросистемы приближенно соответствовало описанию классической механики.

Результат нашего рассмотрения сводится к следующему. Единственной приемлемой пока интерпретацией уравнения Шредингера является статистическая интерпретация, данная Борном. Однако она не описывает реального состояния отдельной системы, а только позволяет делать статистические высказывания об ансамблях систем.

По моему мнению, в принципе неверно класть в основу физики такие теоретические представления, поскольку нельзя отказаться от возможности объективного описания отдельной макросистемы (от описания «реального состояния») без того, чтобы физическая картина мира в известной степени «скрылась в тумане». В конце концов, кажется, неизбежным представление, что физика должна стремиться к описанию реального состояния отдельной системы. Природу в целом можно рассматривать только как отдельную (однократно существующую) систему а не как «ансамбль систем».

Вводные замечания об основных понятиях

А. Эйнштейн, 1953 г., СНТ, т. 3, с. 623 – 626.

Я хочу предпослать нашей работе, написанной совместно с г-жой Б. Кауфман и предназначенной для этого сборника, несколько слов на том единственном языке, на котором я могу говорить свободно. Это — слова извинения. Они должны объяснить, почему несмотря на то, что в сравнительно молодом возрасте я с восхищением воспринял гениальное открытие де Бройлем внутренней связи между дискретными квантовыми состояниями и резонансными состояниями, я все же непрестанно предпринимал попытки найти другой путь, следуя по которому можно было бы дать иной метод решения загадки квантов или, по крайней мере, способствовать подготовке такого решения. В основе этих попыток лежит чувство глубокой неудовлетворенности принципиального характера, которую вызывают у меня основания статистической квантовой теории. Я абсолютно уверен, что и сам де Бройль отнюдь не чужд этого чувства. Это ясно видно из одной его работы двадцатых годов, в которой он предпринял попытку так дополнить квантовую механику, чтобы она давала полное описание конфигурации системы в зависимости от времени в рамках понятий классической механики (материальная точка, потенциальная энергия). В последнее время к этой идее, не зная о работе де Бройля, пришел Д. Бом (теория волны-пилота).

Я нисколько не сомневаюсь, что современная квантовая теория (точнее, «квантовая механика») дает наиболее полное совпадение с опытом, коль скоро в основу описания в качестве элементарных понятий положены понятия материальной точки и потенциальной энергии. Однако то, что я считаю неудовлетворительным в этой теории, состоит в интерпретации, которую дают «ψ-функции». Во всяком случае, в основе моего понимания лежит положение, решительно отвергаемое наиболее крупными современными теоретиками:

Существует нечто вроде «реального состояния» физической системы,, существующего объективно, независимо от какого бы то ни было наблюдения или измерения, которое в принципе можно описать с помощью имеющихся в физике средств. [Какие адекватные средства следует применять для этого, и, следовательно, какими фундаментальными понятиями следует воспользоваться, на мой взгляд, пока неизвестно. (Материальная точка? Поле? Какое-либо другое средство описания, которое надо еще найти?)]. Этот тезис о реальности сам по себе не имеет ясного смысла ввиду своего-«метафизического» характера, он носит лишь программный характер. Однако все люди, в том числе и теоретики, занимающиеся квантовой механикой, твердо придерживаются этого положения о реальности до тех пор, пока не обсуждаются основы квантовой механики. Никто, например, не сомневается в том, что центр тяжести Луны в некоторый наперед заданный момент времени занимает вполне определенное положение даже в том случае, если нет никакого (реального или потенциального) наблюдателя. Если же отбросить этот произвольный тезис о реальности, рассматриваемый в чисто логическом плане, то будет весьма трудно избежать солипсизма. В силу сказанного я отнюдь не стыжусь сделать понятие «реального состояния физической системы» центральным пунктом своих рассуждений.

Теперь нет никаких сомнений в том, что ψ-функция является некоторым способом описания «реального состояния». Вопрос состоит лишь в том, полно или неполно такое описание реального состояния. Всякий раз, когда пытаются дать ответ на этот вопрос, сталкиваются с некоторыми трудностями.

Первое предположение: описание полно. В этом случае, согласно уравнению Шредингера, тело, на которое не действуют никакие силы, плавает в пространстве, занимая тем менее определенное положение (относительно инерциальной системы), чем медленнее оно движется, будучи предоставленным самому себе. Но последующее наблюдение с помощью света позволяет почти точно указать его положение. Если бы описание с помощью ψ-функции действительно было полным описанием системы, мы должны были бы заключить, что найденное нами вначале почти точное положение тела представляет собой следствие наблюдения, но не существует до этих наблюдений. Однако это заключение противоречит интуиции, если речь идет о каком-нибудь макроскопическом теле, а не об электроне или атоме. (То обстоятельство, что создание большой неопределенности положения для тела значительной массы по этой теории требует длительного промежутка времени, не может помочь, поскольку эти промежутки не столь уж велики даже для тел, которые еще можно считать микроскопическими.) С точки зрения этой теории не может представиться и такой случай, когда положение тела в начальный момент времени должно быть задано почти точно.

Поэтому описание системы с помощью ψ-функции приходится считать неполным описанием реальных состояний. Имеются и другие соображения которые приводят к тому же заключению. Аппарат квантовой теории таков, что ψ-функция одной подсистемы некоторой полной системы, состоящей из двух подсистем, изменяется в зависимости от характера (полного) измерения, производимого над второй подсистемой. Так происходит даже в том случае, если обе подсистемы к тому времени, когда производится измерение, оказываются разделенными в пространстве. Если бы ψ-функ-ция давала полное описание реального состояния, то это бы означало, что измерение, производимое над второй подсистемой, оказывает влияние на реальное состояние первой подсистемы. Это соответствовало бы существованию какой-то непосредственной связи между двумя пространственно разделенными объектами. Однако этот случай также отвергается интуицией. Таким образом, и в этом случае приходят к выводу, что описание состояния с помощью ψ-функции следует считать неполным.

Второе предположение: описание с помощью ψ-функции неполно. В этом случае приходится прийти к выводу о том, что должно существовать некоторое более полное описание. Кроме того, высказывается мнение,, что в подлинных законах природы должны фигурировать данные полного, а отнюдь не неполного описания. Трудно также удержаться от подозрения, что статистический характер теории обусловлен, по-видимому, неполнотой описания и не имеет никакого отношения к природе вещей.

Подобные соображения вполне могли бы сыграть определенную роль, и при разработке «теории волны-пилота». Во всяком случае эта теория обходит указанные выше трудности. Сам Л. де Бройль недавно показал, почему он отказался от этого выхода. Теория броуновского движения, в основу которой положены классическая механика и закон осмотического давления, вряд ли могла служить исходным пунктом для создания молекулярно-кинетической теории, если бы теория броуновского движения хронологически предшествовала последней. Мне кажется, что статистическая квантовая теория столь же мало пригодна в качестве исходного пункта для построения более полной теории.

Следующие соображения еще более укрепили меня в этом мнении. Статистическая квантовая теория отчасти обязана своим возникновением тому обстоятельству, что кажущиеся сколь угодно малыми воздействия могут привести к конечным изменениям состояния системы. Например, комптон-эффект показывает, что цуг волн произвольно малой амплитуды и конечной протяженности может передать некоторую конечную энергию электрону. Дело обстоит так, как если бы слабое поле могло бы вызвать не непосредственно перенос конечного количества энергии, а создавало бы лишь небольшую вероятность такого переноса. Но чтобы вероятность какого-то изменения можно было рассматривать как истинное изменение состояния электрона, следует придать смысл «квантовому состоянию», которое в данном случае представляет собой суперпозицию индивидуальных состояний электронов с различной энергией; при этом каждому из этих состояний отвечает некоторая амплитуда вероятности. Таким образом, появляется возможность сопоставить действие слабого поля малому изменению амплитуды вероятности, т. е. «состояния», и тем самым математически свести кажущийся дискретным процесс с конечной скоростью изменения к непрерывному изменению амплитуды вероятности.

Ценой, которую приходится платить за такое сведение одного процесса к другому, служит введение реальных состояний, включающих в себя бесконечно большое число состояний с различной энергией. Необходимость этой жертвы вызвана тем, что мы надеемся постичь физическую природу взаимодействия (в данном случае — слабое и ограниченное в пространстве волновое поле). Это связано с тем, что в квантовой механике сохраняется классическое понятие силы и, соответственно, потенциальной -энергии, и только закон движения: заменяется чем-то совсем новым. Совершенство математического аппарата теории и ее значительный успех скрывают от нашего взора тяжесть тех жертв, которые приходится приносить для этого.

Однако мне кажется, что в конце концов выяснится, что вместо действующей силы и, соответственно, потенциальной энергии (или — в случае комптон-эффекта — волнового поля) следует принять нечто, обладающее атомистической структурой в том же смысле, что и сам электрон. Тогда вообще не будет «слабых полей» и, соответственно, сил как действующего «начала, так же как не существует смешанных состояний.

Еще одно последнее замечание: мои усилия пополнить общую теорию относительности путем обобщения уравнений гравитации были предприняты отчасти в связи с предположением о том, что, по-видимому, разумная общая релятивистская теория поля, возможно, могла бы дать ключ к более совершенной квантовой теории. Это — скромная надежда, но никак не убеждение. Имеются веские аргументы против мнения, что описание реальности, основанное на дифференциальных уравнениях (теория поля), может, вообще говоря, согласоваться с атомистическим характером реальности. Однако эти соображения, насколько я могу судить, не являются обязательными, и у нас до сих пор вообще нет никакого другого пути для формулировки общерелятивистских законов.