Критика теории относительности

О.Е. Акимов

6. Парадокс штриха для координат

Самым удивительным выводом специальной теории относительности является положение об изменении пространственно-временных масштабов. Любой школьник знает, что быстро движущийся стержень в направлении своего движения сокращается. Мюоны, летящие с верхних слоев атмосферы, успевают достичь поверхности Земли, хотя время их жизни в лабораторных условиях ничтожно мало. Этот факт призван подтвердить теоретическое утверждение релятивистов, согласно которому время быстро движущихся объектов замедляется.

На вывод формул сокращения длины и замедления времени в книгах и учебниках по физике отводится одна-две странички. Этот мировоззренческий вопрос всем авторам представляется настолько простым и очевидным, что они не видят нужды посвящать ему больше места. Но давайте внимательно проследим, все ли здесь так просто? Далее нас будут интересовать преобразования Лоренца и вытекающие из них следствия философского значения.

Пусть «штрихованная» координатная система K'(x', ct') движется относительно покоящейся, «нештрихованной» координатной системы K(x, ct). Ниже показывается, что в теории относительности никогда не существовал, не существует и в принципе существовать не может критерий выбора между двумя формулами сокращения длины:

  и    ,

и двумя формулами замедления времени:

  и    ,

Другими словами, даже после того как недвусмысленно заявлено, что штрихованная система отсчета движется, а нештрихованная покоится, нельзя определенно сказать, какой из отрезков короче: тот, что находится в движущейся системе (Δx'), или тот, что находится в покоящейся системе (Δx). Или, еще иначе, какие из неравенств верны:

Δx < Δx' или Δx > Δx',     Δt < Δt' или Δt > Δt'.

В этом состоит суть парадокса штриха, затрагивающего пространственно-временные координаты . Таким образом, неопределенность дробей a = b/c и a = c/b или неопределенность расстановки штриха распространяется не только на частоту, период и длину волны, фигурирующие в релятивистских формулах Доплер-эффекта, но также на пространство и время, что является закономерным следствием спекулятивного характера всей релятивистской теории, поскольку все названные величины взаимосвязаны.

Когда впервые начинаешь говорить об этом противоречии, релятивисты, как правило, не сразу понимают, о чем идет речь. Они долго отказываются верить существующей пестроте формул и набрасываются на критика, обвиняя его в непонимании «самых элементарных вещей». И, тем не менее, путаница в формулах и их толковании налицо.

Причина неоднозначности состоит в том, что вывод формул сокращения длины и замедления времени различными авторами производится по-разному, в зависимости от того, какими преобразованиями Лоренца – прямыми или обратными – они пользуются. Этот математический произвол порождает неопределенность в расстановке штриха, что, в свою очередь, вызывает серьезные затруднения в физическом толковании формул. Тут же возникает вопрос: а почему, собственно, отсутствует критерий на применение прямых и обратных преобразований Лоренца? Что мешает авторам сделать однозначный выбор при рассмотрении конкретной ситуации с наблюдателями? Корни указанной проблемы лежат не в плоскости математики и физики, а зарыты в ложную релятивистскую эпистемологию.

Дело в том, что помимо объектных наблюдателей, неизменно присутствующих в рассуждениях релятивистов, есть еще субъектный метанаблюдатель, т.е. сам исследователь. Релятивисты никогда не делали различий между объектом и субъектом теории. Между тем это смешение приводит к противоречиям, известным из логики. Далее мы покажем, что вопрос о выборе типа преобразований Лоренца (прямое или обратное) субъект теории не в состоянии решить однозначно. Это — системная ошибка релятивистской концепции, от которой сейчас, по прошествию века, не возможно избавиться.

Правда, при зарождении теории относительности, всё ещё можно было поправить путем наложения специальной конвенции. Ведь теория относительности во многом носит конвенциальный характер. Для этого нужно было однозначно указать местоположение метанаблюдателя. Тогда формулы сокращения длины и замедления времени выводились бы либо только из прямых, либо только из обратных преобразований Лоренца. В этом случае ошибка была бы хорошо замаскирована вместе с конвенцией об измерении отрезков с помощью луча света или конвенцией о постоянстве скорости света относительно движущегося приемника.

Однако этого не было сделано сразу, в момент провозглашения двух известных постулатов. Теперь же всё настолько запутано, что любой вдумчивый читатель вправе потребовать решение проблемы по существу, т.е. с точки зрения сложившейся практики. Сейчас в многочисленных учебниках и справочниках примерно в равной пропорции можно обнаружить по паре противоположных формул для замедления времени и сокращения длины, которые дают четыре различных варианта масштабных преобразований. Релятивисты не могут найти этой неоднозначности разумное объяснение. Между тем, как было сказано, она поддается рациональному объяснению, если встать на позицию логического разграничения объекта и субъекта теории.

Чтобы лучше понять, о чем идет речь, когда говорят о парадоксе штриха для координат, приведем выдержку из известного учебника Ландау и Лифшица по теоретической физике, в котором изложены наиболее устоявшиеся положения. В этом учебнике, как это и принято в подавляющем большинстве случаев, через K' обозначена движущаяся система отсчета, а покоящуюся – через K.

«Пусть в системе K покоится линейка, параллельная оси x, – пишут Ландау и Лифшиц. – Длина ее, измеренная в этой системе, пусть будет Δx = x₂ – x₁ (x₂ и x₁ – координаты концов линейки в системе K). Найдем теперь длину этого стержня, измеренную в системе K'. Для этого надо найти координаты обоих концов стержня (x'₂ и x'₁) в этой системе в один и тот же момент времени t'. Из (4.3) находим:

,     .

Длина стержня в системе K' есть Δx' = x'₂ – x'₁; вычитая x₁ из x₂, находим:

.

Собственной длиной стержня называется его длина в той системе отсчета, в которой он покоится. Обозначим ее через l₀ = Δx, а длину того же стержня в какой-либо системе отсчета K' – через l. Тогда

,     (4.5)

Таким образом, самую большую длину стержень имеет в той системе отсчета, где он покоится. Длина его в системе, в которой он движется со скоростью v, уменьшается в отношении . Этот результат теории относительности называется лоренцевым сокращением» [1].

Теперь сравним приведенный вывод формулы для лоренцева сокращения длины, принадлежащий Ландау и Лифшицу, с тем, что по этому поводу говорится в известной книге Макса Борна:

«Итак, – пишет Борн, – мы должны определить длину линейки в системе S'(x', ct'), движущейся относительно S(x, ct)... Пусть l₀  – длина линейки в системе отсчета S', в которой линейка покоится; l₀  называют статической, или собственной, длиной линейки. Два конца линейки имеют координаты, скажем, x'₁ и x'₂, так что x'₂ – x'₁ = l₀ .

При наблюдении этой линейки из системы S мы по первой из формул (70а) имеем:

,      .

где x₁, t₁ и x₂, t₂ представляют собой координаты точек x'₁ и x'₂ в системе S. Пусть теперь мы хотим измерить длину линейки в системе S; это значит, что нужно определить координаты x₁ и x₂ одновременно относительно часов системы S – мы должны положить t₁ = t₂. Выполняя это и вычитая первое из выписанных нами уравнений из второго, мы получаем

.

Полагая x₂ – x₁ = l, мы можем записать

.     (74)

Эта формула утверждает, что длина линейки в системе S оказывается уменьшенной в отношении к 1 в точном согласии с гипотезой сокращения, предложенной Фитцжеральдом и Лоренцем» [2].

Таким образом, Ландау – Лифшиц вывели формулу для лоренцева сокращения из прямых преобразований, а Борн – из обратных. Выражения (4.5) и (74) в приведенных текстах только внешне выглядят одинаково, фактически же они противоположного свойства. В первом случае принято l₀ = Δx и l = Δx' ; во втором, напротив, – l₀ = Δx' и l = Δx. Таким образом, в первом случае имеем формулу:

.     (5.1)

а во втором –

.     (5.2)

У релятивистов тут же находится «простое решение»: «Да здесь срабатывает обыкновенный принцип относительности, – говорят они. – С позиции наблюдателя штрихованной системы линейка, находящаяся в нештрихованной системе, сокращается; и, наоборот, с позиции наблюдателя нештрихованной системы линейка, находящаяся в штрихованной системе, тоже будет сокращаться аналогичным образом. Эти два отношения и отражаются двумя различными формулами – (5.1) и (5.2)».

Однако, после внимательного прочтения обеих книг, мы убеждаемся, что подобное объяснение в данном конкретном случае не годится. И авторы первой работы, и автор второй работы предполагали одну и ту же ситуацию, а именно: штрихованная система – движется, а нештрихованная – покоится. Если бы было так, как рассказывают релятивисты, то нужно было бы в одном случае принимать штрихованную систему за движущуюся, а в другом, эту же штрихованную систему считать уже покоящейся. Но такой вариант исключен; в обоих случаях штрихованная система была движущейся.

Хорошо, давайте не будем прислушиваться к объяснениям релятивистов, а попытаемся самостоятельно установить причину расхождения в формулах.

Итак, в случае с формулой (5.1) рассуждения могли бы выглядеть так. Наблюдатель покоящейся система K следит за движущимся отрезком Δx', то есть наблюдатель нештрихованной системы определяет неизвестную ему длину Δx по известной длине Δx'. Поэтому в качестве исходных преобразований он выбирает прямые преобразования Лоренца. Однако в результате такого выбора получается, что укорачивается непосредственно сам движущейся отрезок Δx', а не его воспринимаемый со стороны образ Δx. Налицо абсолютное или собственное сокращение длины.

Отсюда вторая схема рассуждения, относящаяся к формуле (5.2), с точки зрения теории относительности, кажется предпочтительней, поскольку она как будто бы учитывает факт относительного сокращения длины. Но поскольку в этом случае используются обратные преобразования Лоренца, т.е. ищется неизвестная длина Δx' по известной длине Δx, измерение здесь производит наблюдатель штрихованной системы. В итоге этих двух схем рассуждения, возникла неопределенность, выраженная двумя противоречивыми неравенствами: Δx < Δx' и Δx > Δx', или двумя дробями: Δx/Δx' < 1 и Δx/Δx' > 1, толкование которых принципиальным образом расходится.

Аналогичная неопределенность в расстановке штриха существует и в отношении периодов времени. Вот как получили формулу для собственного времени Ландау – Лифшиц.

«Предположим, – пишут они, – что мы наблюдаем из некоторой инерциальной системы отсчета произвольным образом движущиеся относительно нас часы. В каждый отдельный момент времени это движение можно рассматривать как равномерное. Поэтому в каждый момент времени можно ввести неподвижно связанную с движущимися часами систему координат, которая (вместе с часами) будет являться тоже инерциальной системой отсчета.

В течение бесконечно малого промежутка времени dt (по неподвижным, т.е. связанным с нами, часам) движущиеся часы проходят расстояние . Спрашивается, какой промежуток времени dt' покажут при этом движущиеся часы. В системе координат, связанной с движущимися часами, последние покоятся, т.е. dx' = dy' = dz' = 0. В силу инвариантности интервала

ds² = c²dt² – dx² – dy² – dz² = c²(dt')²,

откуда

.

Но

,

где v есть скорость движущихся часов; поэтому

.     (3.1)

Интегрируя это выражение, можно найти промежуток времени, показываемый движущимися часами, если по неподвижным часам пройдет время t₂ = t₁:

.     (3.2) .

Время, отсчитываемое по часам, движущимся вместе с данным объектом, называется собственным временем этого объекта. Формулы (3.1) и (3.2) выражают собственное время через время системы отсчета, относительно которой рассматривается движение.

Как видно из (3.1) и (3.2), собственное время движущегося объекта всегда меньше, чем соответствующий промежуток времени в неподвижной системе. Другими словами, движущиеся часы идут медленнее неподвижных» [3].

Таким образом, авторы этого учебника фактически вывели формулу:

,     (5.3)

воспользовавшись инвариантной формулой для квадрата интервала:

(cΔt')² – (Δx')² = (cΔt)² – (Δx)²,

путем принятия условия Δx' = 0:

(cΔt' )² = (cΔt)² – (Δx)²,

откуда и получилась формула (5.3).

Ситуация с замедлением времени должна быть аналогична ситуации с сокращением длины, если исходить из прямых и обратных преобразований Лоренца. Однако в отношении времени некоторые авторы предпочитают рассуждать иначе. Так, для вывода формулы через прямые преобразования Лоренца принимают условие Δx' = 0, тогда

  = ,    т.е. .

При выводе этой же формулы через обратные преобразования условие Δx' = 0 трансформируется в новое условие, а именно: Δx = vΔt. В самом деле, из обратных преобразований Лоренца при выполнении условия Δx' = 0, получаем

,      .

Из первой формулы находим новое условие Δx = vΔt. Подставляя его во вторую формулу, вновь получаем выражение (5.3):

  =      =   .

Таким образом, мы показали, как можно вывести одну и ту же формулу (5.3), пользуясь противоположными (прямыми и обратными) преобразованиями Лоренца. Именно последним способом воспользовался Макс Борн в упомянутой книге:

«Для того чтобы вычислить величину удлинения [заметьте, Борн говорит об удлинении времени, а не об укорочении, что, в общем-то, с точки зрения его формулы, логично], рассмотрим начавшийся в момент времени t₁' и закончившийся в момент t₂' период времени t₀, который отсчитали часы, покоящиеся в системе S' ; очевидно, t₂' – t₁' = t₀. Из второй формулы (70а) мы получаем

,      .

Весь период времени t₀ мы измеряем в пространственной точке x₁' = x₂', где расположены часы системы S'. Из первой формулы (70а) следует, что x₂ – x₁ = v(t₂ – t₁), так как наши часы имеют скорость v относительно системы S. Отнимем t₁' от t₂':

   =       =

=   (t₂ – t₁) .

Таким образом, период времени t = t₂ – t₁, протекший в системе S, связан с периодом времени t₀ в системе S' соотношением

      (75).

Это удлинение (замедление) времени противоположно по характеру сокращению длины. Разумеется, с обратной точки зрения единица времени по часам, покоящимся в системе S, оказывается увеличенной в системе S'...

Время, которое показывают часы, покоящиеся в выбранной системе отсчета, называется собственным временем системы» [4].

В результате чисто символически формула замедления времени по Борну совпала с формулой замедления времени по Ландау – Лифшицу, но интерпретировали они ее по-разному. В частности, Борн специально подчеркивает, что характер замедления времени противоположен характеру сокращения длины; термин замедление для него означает удлинение временного периода. Для Ландау и Лифшица замедление времени означает сокращение; у них уже получилось, что характер изменения и длины, и времени один и тот же. Обращаем внимание также на то, что формулы сокращения длины и замедления времени, полученные другим известным немецким физиком, Паули [5], формально совпадают с формулами Борна, а наш соотечественник Б.Н. Иванов в книге «Принципы современной физики» предпочел воспроизвести комбинацию формул Ландау – Лифшица [6]. И на чьей же стороне правда?

Возьмем наудачу какой-нибудь учебник по физике, где рассматривался бы тот же самый вопрос, и сравним с тем, что мы только что привели. Пусть этим учебником будет «Механика» – известный в нашей стране и мире Берклеевский курс физики. В нем мы читаем:

«Слово замедление по отношению к часам означает удлинение интервала времени. Рассмотрим часы, которые неподвижны в системе отсчета S. Результат измерения интервала времени в системе отсчета, в которой часы неподвижны, обозначается буквой t и называется собственным интервалом времени. Предположим, что часы расположены в начале координат системы отсчета S, т.е. в точке, где x = 0. Применяя преобразование Лоренца

при постоянной величине x, получаем для величины интервала времени t', измеренного часами в системе отсчета S', движущейся со скоростью v относительно системы S, в которой находятся первые часы:

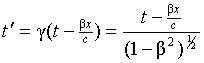
.       (31)

Интервал времени, измеренный в движущейся системе отсчета S', длиннее интервала времени в системе отсчета S.

Это явление называется замедлением времени. Кажется, что движущиеся часы идут медленнее находящихся в покое. Это нелегко понять интуитивно; пройдет, может быть, неделя или год, пока вы уловите смысл замедления времени» [7].

В наших обозначениях формула (31) из приведенной выдержки запишется противоположным образом, чем у Борна, Ландау – Лифшица, зато формула сокращения длины у авторов Берклеевского курса совпала с формулой, выведенной Ландау – Лифшицем. В самом деле, авторы Берклеевского курса пишут:

«Представим себе линейку, лежащую вдоль оси x и неподвижную относительно системы отсчета S. Если линейка неподвижна, то в этой системе отсчета S координаты ее концов x₁ и x₂, не зависят от времени t. Следовательно, величина

(23)     L₀ = x₁ – x₂

представляет собой длину покоя линейки.

Теперь будем рассматривать эту линейку в системе отсчета S', движущейся со скоростью v относительно системы S, в которой линейка неподвижна. Для измерения длины линейки в системе S' мы определяем координаты точек x'₁ и x'₂, совпадающих в данный момент t' с концами линейки. Естественно определить длину линейки L в движущейся системе отсчета S' как расстояние между точками x'₁ и x'₂, которые одновременно (в системе отсчета S' ) совпадают с конечными точками линейки:

(24)     L = x'₁ – x'₂.

На основании преобразований Лоренца (15) получаем

(25)     x₂ = x'₂(t')γ + ct' βγ,    x₁ = x'₁(t')γ + ct' βγ,  

(26)     x₁ – x₂ = L₀ = [x'₂(t') – x'₁(t' )] γ = Lγ.

Таким образом,

(27)     L = L₀/γ = L₀(1 – β²)^1/2.

При этом мы пользуемся нашим определением γ : γ = (1 – β²)^1/2. Это отношение длин представляет собой лоренц-фитцджеральдово сокращение размера линейки, движущейся параллельно своей длине» [8].

Берклеевскую комбинацию формул сокращения длины и замедления времени повторяет, например, Жан Россель в своем известном курсе «Общая физика» [9].

У нас осталась найти последнее сочетания формул для пространственного и временного изменения. Такую комбинацию изменения эталонов длины и времени удается найти в многократно издаваемом учебнике В.Г. Левича, который, как и Ландау – Лифшиц, определенно высказался в пользу сокращения, т.е. уменьшения, а не увеличения, временного периода движущихся часов (длительности процессов). Чтобы быть предельно точным и самим не внести какой-нибудь путаницы, мы целиком воспроизведем интересующие нас выдержки.

«Рассмотрим прежде всего, – пишет Левич, – понятие пространственной протяженности (длины). Пусть в некоторой системе K' покоится некоторое тело, которое мы в дальнейшем будем именовать масштабом. На масштаб не действуют какие-либо силы, которые могут его деформировать и изменить его размеры. Длину масштаба в направлении движения (оси x' ) обозначим через L₀. Эту длину, измеренную в той системе отсчета, в которой масштаб покоится (система K' ), мы будем называть собственной длиной масштаба. С помощью преобразований Лоренца найдем длину масштаба в системе отсчета K, т.е. длину масштаба, движущегося относительно системы K со скоростью v. Пусть в системе K' координаты начала и конца масштаба будут соответственно x'₁ и x'₂. Найдем эти координаты в системе K.

Поскольку масштаб движется относительно системы отсчета K, для измерения его размеров необходимо зафиксировать координаты его начала и конца в один и тот же момент времени, измеренного в системе отсчета K. Для фактического осуществления этого измерения можно было бы зафиксировать в момент времени t положения начала и конца масштаба с помощью светового сигнала, выходящего из системы K'.

Пусть в некоторый момент времени t в системе K начало и конец масштаба имеют координаты x₁ и x₂. С помощью формулы (5, 6а) находим:

,      .

Вычитая, имеем

,

или, обозначая разность координат начала и конца масштаба (длину масштаба в системе K) через L, получаем

.     (6,1)

Мы видим, что длина масштаба, движущегося со скоростью v по отношению к системе K, оказывается меньшей, чем его собственная длина в 1 : раз. Это сокращение размеров тела часто именуется лоренцевым сокращением... Пусть в некоторой точке x' в системе K' происходит некоторый физический процесс в течение промежутка времени Δt₀ = t'₁ – t'₂, где t'₁ и t'₂ – время начала и конца процесса. Тогда в системе K для момента t₁ и t₂ можно написать:

,      .

Вычитая, находим промежуток времени, прошедший от начала до конца процесса в системе K:

.     (6,3)

Время Δt₀, измеренное в системе отсчета, движущейся вместе с телом, в котором происходит процесс, называется собственным временем.

Формула (6,3) показывает, что собственное время Δt₀ между двумя физическими события меньше, чем время, прошедшее между этими событиями в системе K в 1 : раз.

В теории относительности принято обычно говорить о сравнении хода часов в различных инерциальных системах отсчета. При этом под часами понимают произвольный периодический процесс. Тогда можно сказать, что время, показываемое часами, зависит от скорости их движения. Движущиеся относительно некоторой системы отсчета часы, с точки зрения этой системы, идут медленнее, чем часы, покоящейся в этой системе отсчета (но совершенно идентичны с движущимися).

Таким образом, в отличие от ньютоновой физики, течение времени оказывается зависящим от состояния движения. Не существует универсального мирового времени, и понятие промежутка времени между двумя физическими событиями оказывается относительным. Необходимо тут же подчеркнуть, что имеется полная взаимность между системами отсчета K и K'. Предыдущие рассуждения можно было бы обратить. Если физический процесс происходит в точке x в системе K и имеет длительность Δt, то в системе K' он будет иметь длительность

,

как это видно из преобразований Лоренца (5,6а) – (5,6г).

Формулы (6,3) для изменения хода часов была проверена на опыте несколькими способами. Наиболее наглядным из них является следующий. В космических лучах наблюдается распад положительного μ⁺-мезона и отрицательного μ^–-мезона (с массой 215 электронных масс) на позитрон (электрон) и два нейтрино. При этом наблюдался распад μ-мезонов как заторможенных почти до полной остановки, так и на лету, когда они движутся со скоростью, близкой к скорости света. Времена жизни покоящегося и движущегося мезонов связаны релятивистским соотношением

.

Поскольку v близко к скорости света, τ_движ. должно быть значительно больше τ_пок.

Ряд экспериментальных методов позволяет определить значение τ_пок., которое оказалось равным 2 · 10^–6 сек. Если бы время жизни мезонов не зависело от скорости, они пролетели бы путь, равный v · τ_пок. ≈ 600 м (при v ≈ c). В действительности, как показывают измерения, мезоны распадаются, пройдя путь около 20 км. Такому пробегу отвечает время жизни τ_движ. = 20 км/c = 7 · 10^–5 сек = 50τ_пок.. Релятивистское изменение времени жизни оказывается в этом случае весьма большим эффектом» [10].

У Левича мы наблюдаем самые сбивчивые из приведенных выше рассуждений относительно времени, так как формула (6,3), которую он вывел из прямых преобразований Лоренца, противоположна последней его формуле, к которой он привязывает эксперимент с мезонами. Говоря о «взаимности между системами отсчета K и K' », Левич обязан был предупредить читателя, что при обращении формулы замедления времени систему отсчета K' надо считать покоящейся, а K – движущейся, однако он этого не сделал. Больше того, последняя формула однозначно перечеркивает его вывод формулы (6,3), так что в итоге мы имеем две однотипных формулы сокращения длины и времени, противоположных по своим свойствам формулам Ландау – Лифшица.

Путаница, возникшая в формуле, относящейся к длительности процесса, особенно примечательна, так как чисто психологически человеку трудно представить факт замедление времени: то ли это сокращение времени, то ли это его удлинение. В связи с этой психолингвистической неопределенностью любопытно отметить, что надпись и формула под одним из поясняющих рисунков (рис. 11.15) в Берклеевском курсе, иллюстрирующем явление замедления времени, тоже противоречит содержанию и формуле основного текста. Видимо, у трех авторов были различные представления на этот счет, о чем они, быть может, и не догадывались, подготавливая книгу к публикации.

Нам остается рассмотреть, как выглядят первоначальные формулы изменения движущихся масштабов у Альберта Эйнштейна, с каким из четырех представленных здесь вариантов он совпадет. В первой своей работе 1905 года в отношении сокращения длины он писал:

«Рассмотрим твердый шар радиуса R, находящийся в покое относительно движущейся системы κ, причем центр шара совпадает с началом координат системы k. Уравнение поверхности этого шара, движущегося относительно системы K со скоростью v, имеет вид

ξ² + η² + ζ² = R²

Уравнение этой поверхности, выраженное через x, y, z в момент времени t = 0 будет

.

Следовательно, твердое тело, которое в покоящемся состоянии имеет форму шара, в движущемся состоянии – при наблюдении из покоящейся системы – принимает форму эллипсоида вращения с полуосями R, R, R» [11].

Приведем аналогичное место из другой эйнштейновской работы, которая имеет разъясняющее примечание.

«Далее, – пишет Эйнштейн, – возникает вопрос: чему равна в системе K длина l стержня, покоящегося в системе K', ориентированного параллельно оси x' и обладающего длиной l' в системе K' ? Первое из указанных уравнений преобразования дает ответ: l = l' .

Примечание. Для обоих концов линейки, именно для их координат x, выполняются уравнения

,      ,

откуда после вычислений следует

  или    .

Это означает следующее. Если стержень в покое обладает длиной l', то при движении со скоростью v вдоль своей оси он будет обладать с точки зрения несопутствующего наблюдателя меньшей длиной , тогда как для сопутствующего наблюдателя длина стержня, как и прежде, равна l' » [12].

По поводу времени Эйнштейн написал в этой работе так:

«Пусть в начале координат системы K' находятся часы с секундной стрелкой. Для них всегда x' = 0, и они отсчитывают свои секунды в моменты времени t' = 0, 1, 2, 3 и т.д. Первое и четвертое уравнения преобразования дают для времени t этих секундных отсчетов значения

t = ,    ,    ,      и т.д.

Таким образом, в системе K время между отсчетами часов равно 1 :  , т.е. больше секунды. Часы, движущиеся со скоростью v идут – с точки зрения несопутствующей системы координат – медленнее, чем шли бы те же часы, если бы они покоились» [13].

Итак, формулы Борна и Паули совпали с формулами Эйнштейна. Для удобства сравнения все варианты формул сокращения длины и замедления времени при условии, что штрихованная система отсчета движется, а нештрихованная покоится, сведены в табл. 5.1.

Таблица 5.1

Комбинация	Авторы	Эталоны длины	Эталоны времени
Первая	Эйнштейн, Борн, Паули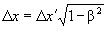
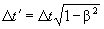Вторая	Курс Ландау – Лифшица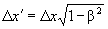
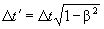Третья	Берклеевский курс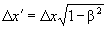
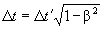Четвертая	Курс Левича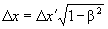

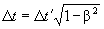Теперь давайте попытаемся осмыслить неоднозначность формул. На первый взгляд кажется, что авторы всех книг по теории относительности пишут об одном и том же: длина движущихся отрезков сокращается, а время замедляется. И вот мы начинаем разбираться, что означают эти слова на языке формул. Оказывается, математические выражения для изменения длины и времени у авторитетных релятивистов выглядят взаимоисключающими.

Сейчас мы можем только догадываться, почему, скажем, Ландау – Лифшиц приняли однотипный характер изменения пространственно-временных эталонов. Видимо, они полагали, что прямые и обратные преобразования Лоренца симметричны относительно радикала и не может получаться так, что при нахождении метрических масштабов в одном случае радикал оказывался в числителе, в другом — в знаменателе. По диаграмме Минковского временная и пространственная оси наклонены под одним и тем же углом, поэтому и масштабные единицы должны меняться одинаково. Так что, с точки зрения геометрии, они были, возможно, ближе к истине: пространственные отрезки и периоды времени у них менялись единообразно как сокращение и уменьшение относительно исходных эталонов длины и времени.

Можно понять и оправдать позицию Борна и Паули, которые писали свои книги вскоре после публикации Эйнштейна. Эти авторы хотели сделать эйнштейновские выкладки математически более прозрачными, но не решались исправить первоначальную формулу и толкование замедления в смысле удлинения времени. Как бы там ни было, нам сейчас ясно, что математика здесь играет подчиненную, чисто иллюстративную роль. Она не является необходимым звеном в цепи доказательства некоего утверждения, смысл которого пришел в физику не из математических формул.

Повторяем, если бы многозначность формул была замечена в момент зарождения теории относительности, то можно было конвенциально продекларировать: формулы Эйнштейна являются единственно верными. Сегодня исправлять эту ошибку нельзя. Тысячи профессоров и авторитетных авторов, живших в XX веке и ныне живущих в XXI веке, привыкли писать формулы по-своему. И это помимо того, что мы знаем, как ошибся Эйнштейн в отношении формул для эффекта Доплера. Где гарантия, что этот физик не ошибся еще и в этом случае? Некогда популярная эпистемология позитивизма, сводящаяся к провозглашению постулатов, без понимания существа дела, сегодня многих уже не устроит. Молодое поколение может потребовать каких-то рациональных довод в отношении выбора того или иного варианта пересчета масштабных единиц. Таким образом, на данный момент сложившаяся в течение столетия ситуация представляется нам совершенно тупиковой.

Итак, прежде понятные утверждения о том, что движущиеся часы замедляют свой ход, а движущиеся эталоны длины укорачиваются, получают неожиданное затруднение, когда речь заходит о представлении этих утверждений в математических выражениях. Оказывается, каждый человек вкладывает в них свой индивидуальный, отличный от других, смысл. Как правило, когда говорится о помолодевших космонавтах, летавших в космосе с субсветовыми скоростями, имеется в виду абсолютное замедление их процессов старения. То же самое касается времени жизни космических частиц. Однако сокращение длины их ракет понимается относительно: ведь никто не говорит, что космонавты вернутся на Землю из своей космической командировки на сплющенных ракетах.

На сегодня теоретики релятивизма не договорились о расстановке штриха в соответствующих формулах, откуда ведется наблюдение за объектами — из покоящихся или движущихся координат, а также о том, какими преобразованиями Лоренца пользоваться при выводе формул — прямыми или обратными. Непонятно, что понимать под замедлением времени — его удлинение (dilation) или сокращение (contraction). Имеется несколько вариантов вывода формул, которые несводимы к какому-то одному. Каким именно способом нужно воспользоваться, релятивисты нам не объяснили. Почему в этом исключительно важном для релятивистов пункте происходит сбой, который практически сводит на нет главный вывод всей современной физики?

* * *

Парадокс штриха, связанный с масштабами длины и времени, напоминает парадокс лестницы Шрёдера. Глядя на рис. 6.1, может возникнуть образ либо лестницы, либо нависающего ступенчатого карниза. Почему так происходит?

Рис. 6.1. Лестница Шрёдера. Человек может сначала видеть на первом плане горизонтальные линии системы K. Тогда ему кажется, что по лестнице Шрёдера можно подняться наверх, если начать восхождение справой стороны. Но через некоторое время изображение лестницы как бы переворачивается: линии системы K уходят на второй план, а на первом появляются линии системы K'. Тогда уже видна не лестница, а нависающие ступени карниза. Период колебаний между изображениями лестницы и карнизом колеблется от одной секунды до нескольких минут.

Дело в том, что, помимо непосредственного пространства рисунка – его мы будем называть объектным, – человек обладает еще и своим внутренним психологическим пространством; назовем его субъектным. В зависимости от того, как расположены объектные пространства в субъектном пространстве, мы видим либо лестницу, либо карниз. Если поле верхнего ступенчатого треугольника K' воспринимается нами как плоскость, находящаяся ближе к нам, чем поле нижнего треугольника K, то мы отчетливо видим нависающий карниз; если же поле K' располагается в нашем субъектном пространстве дальше от поля K, то рисунок воспринимается как лестница. Какое поле считать расположенным ближе, а какое дальше не диктуется самим рис. 6.1: каждый смотрящий волен выбрать его по своему усмотрению.

Другое дело, если смотреть на реальную лестницу или карниз. За счет перспективы, которая выражается, скажем, в чуть меньшем расстоянии между горизонтальными полосками ступенчатого треугольника K', наш мозг безошибочно воспринимает конкретный объект.

Тотальный релятивизм не оставляет нам ни единого антисимметричного элемента в отношении систем K' и K. Поэтому сначала к нам приходит уверенность в правильности использования обратных преобразований Лоренца, но через некоторое время эта уверенность куда-то улетучивается, картина перестраивается и мы уже считаем правильным использование прямых преобразований Лоренца. Это происходит периодически и мы не можем остановиться на каком-то одном решении, которое следовало бы назвать истинным.

Указанное психологическое явление целиком переносится на ситуацию с двумя системами координат. Однозначная расстановка штриха в формулах сокращения длины и замедления времени невозможна, все четыре противоречащие друг другу комбинации табл. 6.1 имеют право на существование, т.е. сказать, какое из неравенств единственно правильное – Δx < Δx' или Δx > Δx', Δt < Δt' или Δt > Δt' – совершенно невозможно.

Если будет позволено подобрать геометрический образ для классической и релятивистской физики, мы бы предложили изобразить их в виде двух рам, одна из которых логически верная (рис. 6.2а) — это образ классической физики, — другая ошибочная — это образ релятивистской физики (рис. 6.2б). Релятивисты вводят двух объектных наблюдателей — A₁ и A₂, а конструктивист, придерживающийся канонов классической физики, всегда выступает в роли метанаблюдателя — A₀.

Исходя из принципа относительности наблюдения за рамой, релятивисты могут настаивать, что внутренняя сторона рамы будет хорошо видна обоим объектным наблюдателям. То, что при этом объект теряет свою логическую целостность, и образ рамы становится противоречивым, их мало беспокоит, так как целого они видеть не хотят или не могут. Приверженец же классической физики постоянно уличает их в искажении объекта, как цельного образа исследования; он настаивает на единой и абсолютной системе отсчета, которую обязан занимать субъект теории A₀.

Рис. 6.2. Если классической физике сообщить некий геометрический образ правильной прямоугольной рамы (а), то для релятивистской раму придется вычертить логически противоречивой (б). Это происходит оттого, что приверженец классической физики выступает в роли метанаблюдателя A₀, а релятивист раздваивается на два объектных наблюдателя A₁ и A₂, каждый из которых диктует свою геометрическую логику.

Релятивисты-формалисты, как и конструктивисты, не могут полностью избавиться от абсолютной системы координат, поскольку она является неотъемлемым атрибутом всякого пространственного мышления, однако эту свою привилегированную позицию они используют необъективно, в интересах того или иного объектного наблюдателя. Находясь в относительной координатной системе и делая какие-либо теоретические выводы, метанаблюдатель-реляти­вист примеряется к текущей относительной ситуации, как говорится, входит в положение объектного наблюдателя, но сам он никогда не расстается со своими абсолютными эталонами пространства и времени.

Правдоподобные утверждения объектного наблюдателя A₁ окажутся ложными для объектного наблюдателя A₂, и наоборот. Истина состоит в том, что оба наблюдателя обманываются. Релятивист, взглянув на мир глазами объектного наблюдателя, верит в истинность всего того, что ему показалось. Релятивизм, как философия физики, начинается там, где проводится полное тождество между субъектом теории и объектным наблюдателем, где не делается никаких различий между физическим, психологическим и математическим пространствами. В этом случае происходит эпистемологическое смешение всего относительного, условного и конвенциального с абсолютным, безусловным и физическим.

Наконец, внимательно понаблюдайте за вращающейся девушкой (рис. 6.3). Поскольку дается только ее плоская тень, вы не в состоянии определить, в какую сторону она реально вращается — по часовой стрелке или против часовой стрелки. Сначала вам кажется, что девушка вращается в одну сторону; вдруг, неожиданно для вас она начинает вращаться в противоположную сторону. В этой анимации отсутствует абсолютная система отсчета, которая позволяла бы нам сориентироваться с направлением вращения объекта.

Рис. 6.3. Данным психологическим эффектом восприятия объясняет парадокс штриха, существующий в теории относительности. Сначала вам кажется, что девушка вращается в одну сторону; вдруг, неожиданно для вас она начинает вращаться в противоположную сторону.

Психологический парадокс штриха определенным образом связан и с известным логическим «парадоксом обманщика», который строится следующим образом: «Я обманщик», – сказал обманщик. Итак, обманщик сообщает о себе, что он является таковым. Следовательно, он выступает в своем противоположном качестве, а именно, необманщика. Поэтому сказанное предложение нужно прочитать так: «Я обманщик», – сказал необманщик. Правдивому человеку мы должны верить. Но ведь он сообщает, что он является обманщиком. Таким образом, мы снова возвращаемся к первому предложению. Возникает неопределенность в том, как квалифицировать фразу, заключенную в кавычках: как нечто, соответствующее истине, то есть считать, что она верно характеризует человека, произносящего данное предложение, или же ее надо расценить как ложную.

Парадокс обманщика возник потому, что в данной семантико-лингвистической конструкции не проведена демаркационная линия между субъектом и объектом. Помимо обманщика и необманщика в этой ситуации участвуем мы с вами в роли исследователей, сторонних наблюдателей или скорее метанаблюдателей. Если произвести четкое лингвистическое отделение смыслового содержания, которое должно относиться к нам, как метанаблюдателям, от прочей семантики объектных персонажей, то логическое противоречие будет снято. Вот каким способом нужно представить ситуацию с обманщиком, чтобы исключить из нее двусмысленность:

1. «Я обманщик», – сказал обманщик.
«Это истина», – сказал метанаблюдатель.

2. «Я обманщик», – сказал необманщик.
«Это ложь», – сказал метанаблюдатель.

3. «Я необманщик», – сказал обманщик.
«Это ложь», – сказал метанаблюдатель.

4. «Я необманщик», – сказал необманщик.
«Это истина», – сказал метанаблюдатель.

Здесь два последних высказывания дополняют возможными вариантами ситуацию, представленную в парадоксе обманщика, и делают всю группу высказываний полной. Если приведенные четыре языковые конструкции записать коротко, используя только слова истина и ложь, то обнаружится их сходство с четырьмя возможными вариантами перемножения (+ 1) и (– 1):

1) ложно · ложно = истинно,
( – 1) · ( – 1) = + 1,
враг моего врага – мне друг;

2) истинно · ложно = ложно,
( + 1) · ( – 1) = – 1,
враг моего друга – мне враг;

3) ложно · истинно = ложно,
( – 1) · ( + 1) = – 1,
друг моего врага – мне враг;

4) истинно · истинно = истинно,
( + 1) · ( + 1) = + 1,
друг моего друга – мне друг.

Рядом с перемножением (+ 1) и (– 1) выписаны также известные выражения, где фигурируют слова друг и враг. Парадокс обманщика предупреждает нас о возможных на этом пути осложнениях. Из цепочки отношений – Петр враг Ивана, Иван друг Степана, а Степан враг Кузьмы – однозначно следует, что Петр друг Кузьмы. Этот вывод сделан субъектом теории, т.е. метанаблюдателем. Но нельзя строить конструкцию типа: «Петр обманщик», – сказал Иван. «Это ложь», – сказал Степан. Степан, как объектный персонаж, не должен выносить свою оценку в отношении Петра, Ивана и прочих лиц, непосредственно участвующих в объектной ситуации. Это разрешено делать только метанаблюдателю с безупречной «моральной» характеристикой, который не имеет права лгать. Таким образом, парадокс обманщика говорит нам о том, что попытка метанаблюдателя встать на позицию обманщика или необманщика немедленно приводит к смысловому конфликту.

Для лучшего уяснения этой логической ситуации приведем следующую наглядную картинку. Представим себе два железнодорожных состава, неподвижно стоящих на соседних путях. Два пассажира, находясь каждый в своем поезде, смотрят в окна вагонов друг на друга. Описанную ситуацию можно отразить знакомой нам таблицей умножения:

1) движение · движение = покой;

2) движение · покой = движение;

3) покой · движение = движение;

4) покой · покой = покой.

При плавном движении двух поездов в одном направлении и с одинаковой скоростью пассажирам кажется, что их поезда стоят на месте (1), как если бы оба поезда действительно стояли на месте (4), т.е. возникает неопределенность в выборе пунктов 1 и 4. При плавном движении одного из поездов пассажиры также не в состоянии определить, какой именно из поездов тронулся (неопределенность между пунктами 2 и 3). Объективную ситуацию с движением поездов может правильно оценить лишь провожающий, находящийся на платформе, т.е. метанаблюдатель.

Точно такая же неопределенность возникает у нас в специальной теории относительности при сравнении эталонов длины и времени, находящихся в движущейся и покоящейся системах отсчета. Нельзя построить физическую теорию, основывающуюся исключительно на относительных характеристиках. Психология восприятия и логика, а главное, неоднозначность расстановки штриха в пересчетных формулах, подсказывают нам необходимость введения метанаблюдателя, находящегося в абсолютной системе отсчета. Только в этом единственном случае прямые преобразования Лоренца можно будет привязать к абсолютной системе отсчета и затем вывести из них изменения эталонов длины и времени.

Кстати сказать, до Эйнштейна, т.е. до появления его спекулятивной теории относительности, так оно и было: Лоренц привязывал покоящуюся систему координат, т.е. нештрихованную систему отсчета, к неподвижному эфиру, от которого он никогда не отказывался, а штрихованную систему — с движущимся через эфир электроном. Но когда эфир ликвидировали, тут же исчезла и абсолютная система отсчета. Теперь уже каждый из объектных наблюдателей-релятивистов стал произвольно выбирать либо прямые, либо обратные преобразования координат и получал на их основе то, что ему вздумается. Таким образом, без абсолютной системы отсчета объектный наблюдатель оказывается без точки опоры, т.е. в роли барона Мюнхгаузена, который ухитрился самого себя вытащить из болота.

Релятивисты запрещают в своих мысленных экспериментах вводить абсолютную систему отсчета, а, значит, и метанаблюдателя. Но теоретизирующий человек не может абстрагироваться от самого себя, поэтому метанаблюдатель вместе со своим абсолютным пространством находится на положении «нелегала». Он проявляется то в образе одного объектного наблюдателя, то другого. Совершенно незаметно для себя субъект теории то «расщепляется» на два наблюдателя, находящихся каждый в своей системе отсчета, то вновь «конденсируется» в одно лицо. Смешение функций объектного наблюдателя с субъектным открывает шлюзы для всевозможного рода спекуляций, которые мы и наблюдаем на примере неоднозначности изменения эталонов длины и времени. В общем, в зависимости от ситуации в системах отсчета могут устанавливаться такие отношения, которые удобны с точки зрения общей идеологии теории относительности, но ошибочные по существу. Находясь в некотором привилегированном положении, метанаблюдатель всегда претендует на непогрешимость своих суждений.

Авторы цитируемых нами книг становятся метанаблюдателями неосознанно. Их внимание периодически соскальзывает то на позицию субъекта теории, то объекта, причем один раз их угораздит оказаться в штрихованной системе отсчета, другой раз — в нештрихованной. Так появляется неопределенность в расстановке штриха, поскольку они, как метанаблюдатели, постоянно витают где-то над обеими системами, смешивая, что относительно чего движется. Им порою кажется, что сначала штрихованный эталон больше нештрихованного, затем — наоборот. Мысленно релятивисты скользят как бы по ленте Мёбиуса. Рассуждая сначала в одной плоскости, они незаметно для себя оказываются в другой плоскости, развернутой относительно первой на 180 градусов. Такой логический кульбит объектный наблюдатель способен совершать благодаря абсолютной системе координат метанаблюдателя. Раздвоение сознания — это естественное и постоянное состояние всякого релятивиста.

Метанаблюдатель выказывает свое присутствие, в частности, через термин собственный: если объектный наблюдатель к своим эталонам длины и времени добавляет этот предикат, значит, он претендует на статус метанаблящателя. Собственные эталоны длины и времени определяются как длина отрезка и, соответственно, время таких часов, которые покоятся относительно системы отсчета. Однако, если придерживаться этой дефиниции, легко выявится ее достаточно бессмысленное содержание. Часы, принадлежащие непосредственно данной системе координат, с точки зрения той же теории относительности, показывают то, что они показывают, как бы это тавтологично не звучало, т.е. Δt = Δt, Δt' = Δt' . Когда под предлогом собственного времени вводят новые обозначения – Δt' = T₀, Δt' = T, Δt' = t, Δt' = Δt₀ и т.д. – знайте, вас хотят ввести в заблуждение. Фраза Левича «собственное время Δt₀ между двумя физическими события меньше, чем время, прошедшее между этими событиями в системе K» спекулятивна, поскольку собственный эталон может находиться только в покоящейся системе отсчета; движущиеся часы не могут быть нашей собственностью, они являются собственностью другого объектного наблюдателя.

Ясно, что существовать могут только два эталона часов или два течения времени – время Δt покоящейся системы и время Δt' движущейся системы, которые регистрируются часами, находящимися в покоящейся системе. Последнее условие обязательно, так как время движущейся системы измерять движущимися же вместе с ней часами бессмысленно. Третьего времени, как бы его не называли – собственное или еще как-то – просто быть не может. Оно исключено логикой построения возможных ситуаций.

Аналогично можно сказать и об эталонах длины. Нет большого смысла данным эталоном длины измерять этот же эталон длины. Если такая операция существует, то только благодаря возможности репродуцирования эталонов. Когда же при этом пытаются ввести «двойную бухгалтерию» в виде дублирующих обозначений: Δx' = L₀, Δx = L₀, Δx' = l, Δx' = l₀ и т.д., вместе с ней предоставляется возможность для незаконных махинаций с формулами. 

Например, говорят: «Собственная длина линейки сократилась на треть ее длины». Что это означает? Это означает, что произошло укорочение ее длины к какому-то абстрактному абсолютному эталону, который метанаблюдатель держит в своей голове. Его длина уже не определяется длиной эталонов, находящихся в относительных системах координат. Так говорят, в частности, о сокращении стержня при его охлаждении. Но в теории относительности подобные формулировки недопустимы. Если говорить опять о времени, то в ней не должны возникать эффекты нестарения космонавтов. Впрочем, о парадоксах с нестареющими космонавтами мы еще поговорим.

---

[1] Ландау Д.Д. и Лифшиц Е.М. Теория поля. – М., 1973, с. 24 – 25.
[2] Борн М. Эйнштейновская теория относительности. – М., 1964, с. 299 – 300.
[3] Ландау Д.Д. и Лифшиц Е.М, с. 20 – 21.
[4] Борн М., с. 301 – 302.
[5] Паули В. Теория относительности. – М., 1947, с. 26 – 27.
[6] Иванов Б.Н. Принципы современной физики. – М.: Наука, 1973, с. 19.
[7] Механика. Берклеевский курс физики (БКФ). Т.1. Ч. Киттель, У. Найт, М. Рудерман. – М., 1971, с. 376 – 377.
[8] Там же, с. 373 – 375.
[9] Россель Ж. Общая физика. – М.: Мир, 1964, с. 136.
[10] Левич В.Г. Курс теоретической физики. Т.1. – М.: Физматгиз, 1962, с. 200 – 203.
[11] Эйнштейн А. К электродинамике движущихся тел. СНТ. Т.1. – М.: Наука, 1965, с. 18.
[12] Эйнштейн А. Теория относительности. СНТ. Т.1., с. 419 – 420.
[13] Там же, с. 420.