Критика теории относительности
О.Е. Акимов
8. Пространственные парадоксы
Одной из целей курса «Естествознание» является анализ спекулятивного мышления релятивистов. Задача состоит не только в том, чтобы дать верную формулу взамен ошибочной, как это было сделано в предыдущих разделах, но и раскрыть схоластическую природу методов доказательства, принятых в релятивистской физике.
Немало было сказано в этом отношении, в частности, говорилось, что одним из основных приемов спекулятивной логики является явное, как это было в первой работе Эйнштейна, или неявное введение абсолютного пространства метанаблюдателя. В предыдущем разделе приводилась выдержка из учебника Левича, где тот использовал условные чертежи, в которых отсутствуют истинные геометрические отношения. Этот прием тоже широко используется релятивистами, которые почти никогда не ставят задачи строгой геометрии типа: по двум сторонам треугольника найти третью. Они, как правило, ограничиваются приблизительными графическими чертежами, призванными иллюстрировать их путаные рассуждения. То же самое происходит и с формулами. На примере парадокса штриха мы уже показали, что за словами сокращение длины и замедление времени на самом деле стоят по паре противоположных формул. Получилось так, что релятивизм объектных наблюдателей повлек за собой релятивизм в среде субъектов теории.
Пороки релятивизма нигде так себя не показали, как при решении парадокса часов. На примере этого хорошо известного парадокса мы покажем релятивизм в его более широком смысле, а именно, как философию относительного решения физических проблем. Согласно этой спекулятивной доктрине мы имеем столько точек зрения, сколько ученых занимается данной тематикой. Каждый релятивист-исследователь создает свою индивидуальную теорию или, во всяком случае, имеет свою особую позицию по тому или иному частному вопросу. Проблемы с формулами для доплер-эффекта, замедления времени и сокращения длины, рассмотренные выше, являются следствием этой двусмысленности. Причем указанная неоднозначность, похоже, мало беспокоит релятивистов, они даже и не пытаются устранить многозначность своих формулировок. Парадокс часов служит тому прекрасным доказательством: сколько людей принималось за его анализ, столько и мнений существует по его разрешению.
Суть парадокса часов чрезвычайно проста. Имеем двух объектных наблюдателей А и В строго одного и того же возраста (отсюда еще одно название: парадокс братьев-близнецов). Пусть наблюдатель А движется относительно покоящегося наблюдателя В с субсветовой скоростью. Тогда, согласно положению о замедлении времени, наблюдатель А останется более молодым, чем наблюдатель В. Однако, согласно принципу относительности движения, ситуация обратима: с точки зрения наблюдателя А, движущимся будет наблюдатель В, и тогда уже наблюдатель В должен быть моложе наблюдателя А. Проблема состоит в том, что в рамках релятивистской теории невозможно указать, какой из наблюдателей — А или В — на самом деле окажется моложе другого?
Всякий непредвзято мыслящий человек быстро сообразит, что перед ним не парадокс какой-то содержательной, например, кинематической ситуации, а элементарное формально-логическое противоречие, которое говорит лишь об одном — о несовместимости двух принципиальных условий СТО:
1) асимметричности течения времени для А и В;
2) симметричности относительного движения А и В.
Если по первому условию получилось, что наблюдатель А моложе наблюдателя В (обозначим: А < В), то второе условие моментально приводит к противоречию: наблюдатель В должен быть моложе наблюдателя А (А > В). Утверждения А < В и А > В взаимно исключают друг друга. Этот простой и очевидный факт вопиющего противоречия трудно не признать. Но любовь релятивистов к своему мифу столь безгранична, что они готовы отдать голову на отсечение, только чтоб у них не отняли веру в пенистую Вселенную. В том, что это противоречие носит исключительно формально-логический характер, подтверждается еще и тем, что парадоксу времени можно подобрать пространственный аналог.
* * *
Пусть через проводящий стержень А замыкаются контакты электрической цепи, состоящей из батареи и лампочки, закрепленных на деревянном бруске В (рис. 8.1а). На рис. 8.1б изображен момент, когда брусок В вместе с лампой и батареей проносится мимо проводящего стержня А. В этом случае брусок В сократится в длину, но во время его пролета мимо покоящегося стержня А произойдет замыкание цепи, и лампа на мгновение вспыхнет. На рис. 8.1в изображена ситуация, когда уже проводящий стержень А проносится мимо покоящегося бруска В. В этом случае, за счет укорочения стержня А, замыкание цепи не произойдет, и лампа не вспыхнет. Ситуации, изображенные на двух последних рисунках равноправны, так как удовлетворяют принципу относительности. Спрашивается, произойдет ли в действительности вспышка света или ее не будет?
Рис. 8.1. Парадокс с зажженной лампочкой. Все элементы электрической цепи находятся в покое: лампочка горит, так как цепь замкнута (а). Из-за быстрого перемещения бруска В расстояние между контактами для наблюдателя А сократится, но лампочка на мгновение вспыхнет, так как цепь на некоторое время окажется замкнутой (б). При быстром движении проводящего стержня А для наблюдателя В цепь окажется постоянно разомкнутой и лампочка никогда не вспыхнет (в). Согласно принципу относительности, два последних случая — (б) и (в) — тождественны. Вопрос: что произойдет в действительности — вспыхнет или не вспыхнет лампочка?
Понятно, что это не содержательная задача, а чисто формальная. Ситуация, изображенная на рис. 8.1б (A > B), не совместима с ситуацией, изображенной на рис. 8.1в (A < B). Асимметричность фактического или кажущегося характера (для логики это неважно), возникающая в системах А и В, не совместима с симметричностью (равноправием) систем А и В: либо А > В, либо А < В, но ни в коем случае: и А > В, и А < В. Пытаться решать это противоречие путем привлечения физических законов электротехники (например, исследовать направление тока и величину потенциала), механики (например, за счет введения ускорения и гравитационного потенциала), материаловедения (например, рассмотреть, из какого материала сделаны проводящий стержень и контакты), значит встать на абсолютно спекулятивную почву. Именно на этой ложной основе релятивисты пытаются решить парадокс часов.
При нашем анализе парадокса часов читатель, возможно, удивится многообразию предложенных релятивистами решений. Но он должен проявить к ним определенную снисходительность, если вспомнит, какое разнообразие и какую настойчивость проявляли изобретатели вечных двигателей, а ведь большинство из них были честными учеными. Задачи средневековья по поиску философского камня или панацеи от всех болезней тоже решались далеко не глупыми людьми. Заблуждения Эйнштейна или Борна, как и заблуждения Платона или Аристотеля, достойны самого тщательного изучения, поскольку их ошибки породили застой в науке на очень длительные периоды времени.
Однако прежде чем начать разбирать многообразные предложения по разрешению парадокса, связанного с замедлением времени, давайте проанализируем более детально еще один парадокс, связанный с сокращением длинны. Пространство визуально, следовательно, противоречия, связанные с ним, окажутся более наглядными и доступными пониманию, чего нельзя сказать про менее ощущаемое время. Но это не единственная причина, по которой мы рассматриваем парадокс распиленной линейки — так называется следующее противоречие. Дело в том, что в парадоксе часов, как и в только что представленном парадоксе с лампочкой, участвуют две системы отсчета с двумя объектными наблюдателями, каждый из которых находится в своей системе. Но существует также третий наблюдатель, роль которого неизбежно приходится играть нам с вами. Именно позиция метанаблюдателя вносит элемент неопределенности.
Взгляните еще раз на рис. 8.1. По сути, там изображены три системы отсчета: абсолютная (рис. 8.1а), которая совпадает с полем страницы; первая относительная (рис. 8.1б), в которой проводящий стержень А покоится, и вторая относительная (рис. 8.1в), в которой покоится брусок В. Когда в роли метанаблюдателя оказывается релятивист, он посредством многочисленных переходов из одной системы в другую, из второй — в третью, из третьей — в первую быстро запутывает задачу, так что первоначально прозрачная в логическом отношении ситуация становится неразрешимой. Нам нужно постараться отключить канал, по которому распространяется спекулятивное мышление релятивиста-метанаблюдателя или просто неопытного читателя. Для этого необходимо создать противоречивую ситуацию, типа А < В и А > В, относительно какого-то одного объектного наблюдателя, лишив, таким образом, субъекта теории возможности выхода за рамки собственной системы отсчета.
* * *
Суть парадокса распиленной линейки изложим в виде следующей задачи. Распиленная на две части линейка разгоняется до субсветовых скоростей по направлению своей длины. Согласно специальной теории относительности, для неподвижного наблюдателя размеры движущейся линейки должны сократиться в направлении ее движения. Вопрос: будет ли наблюдаться просвет между двумя сокращенными частями линейки или же линейка сократится так, как если бы она распилена не была (наблюдатель не увидит просвета)? Описанная ситуация проиллюстрирована рис. 8.2, под которым имеется текст с краткой формулировкой предложенной задачи.
Рис. 8.2. Парадокс распиленной линейки. Пусть происходит транспортировка двух кусков линейки — 1 и 2. Если куски транспортируются по отдельности, то сокращение их произойдет так, как показано на Финише (а) и (б). Совместная транспортировка этих кусков ничего не изменит и на Финише между кусками будет виден просвет (в). Однако транспортировка целой линейки приведет к сокращению типа (г). Значит, между кусками не должен наблюдаться просвет (д) — ведь линейка «не знает», что она распилена. Итак, непрнятно, как будет в действительности происходить сокращение транспортируемых кусков линейки — по варианту (в) или же по варианту (д)?
Сейчас мы дадим развернутое условие задачи о распиленной линейке (или распиленном стержне).
Итак, предположим, у вас имеется достаточное количество одинаковых линеек, которые вы можете распиливать на два равных по длине куска — 1 и 2. Пусть со Старта ровно в 3 часа по вашим покоящимся часам (другие часы здесь не участвуют) кусок 1 распиленной линейки начал ускоренное движение. К 5 часам его скорость с нулевого значения достигла величины, близкой к скорости света. Начиная с 5 часов его равноускоренное движение перешло в равномерное и точно в 7 часов правый торец куска 1 поравнялся в правым торцом точно такого же куска 1, неподвижно лежащего на Финише (рис. 8.2а).
Затем точно таким же образом заставим двигаться кусок 2. Он тоже ровно в 3 часа (предположим, следующего дня) начал ускоряться, с 5 часов продолжил свое движение с постоянной скоростью, равной скорости куска 1, а в 7 часов правый торец куска 2 поравнялся с правым торцом точно такого же куска 2, неподвижно лежащего на Финише (рис. 8.2б).
Подчеркнем, что и кусок 1, и кусок 2 распиленной линейки разгонялись одним и тем же способом, испытали равные ускорения, прошли одинаковые расстояния от Старта до Финиша и мимо соответствующих покоящихся кусков прошли в одно и то же время с равными скоростями.
Однако ничто не мешает их совместной транспортировке (рис. 8.2в). В этом случае, стартуя в 3 часа, прекращая равноускоренное движение в 5 часов и финишируя в 7 часов, они должны занять такие же положения, которые они заняли бы, двигаясь порознь. В последнем случае между кусками 1 и 2 мы наблюдаем просвет; его можно было бы зарегистрировать экспериментально, если по одну сторону траектории движения кусков разместить источник света, а по другую — фотодатчик.
Далее осуществляем еще две аналогичные транспортировки: на рис. 8.2г изображены две фазы — на Старте в 3 часа и на Финише в 7 часов — не распиленной линейки; на рис. 8.2д показаны две фазы уже распиленной линейки, когда куски 1 и 2 стартуют вместе. В последнем случае просвета между кусками уже не наблюдается. Логика последнего случая состоит в следующем: линейка «не знает», что она распилена, поэтому кусок 2 ровно в 7 часов должен занять то пространственное положение, которое он занял бы, если бы линейка не была распилена.
Таким образом, не ясно, как поведут себя куски линейки: сократятся ли они так, как если бы они ничего «не знали» друг о друге (рис. 8.2в), т. е. когда они транспортировались поодиночке, или же они «осмыслят» свою принадлежность целому и будут «вести» себя так, как если бы они входили в состав не распиленной линейки (рис. 8.2д)? Получается, что и любому движущемуся с субсветовой скоростью предмету, прежде чем занять соответствующее место в пространстве, придется «осмотреться», нет ли рядом с ним движущихся по его маршруту попутчиков. После того, как предмет «оценит» окружающую обстановку, он должен будет «сделать соответствующий выбор» между двумя возможными вариантами своего движения.
Абсурдность такого положения вещей очевидна: куски линейки не умеют размышлять. Если теория относительности допускает это, если она одинаково успешно предсказывает положение кусков, изображенных на рис. 8.2 в и д, значит, она ошибочна. Никакого сокращения движущихся объектов — ни кажущегося, ни реального — на самом деле не существует.
* * *
Понять причины возникновения парадокса распиленной линейки несложно, если обратить внимание на то, что кусок 1 на рис. 8.2в только сократился, а на рис. 8.2д он еще и сместился на некоторое расстояние вправо. Если каждую половину стержня связать со своей собственной системой отсчета, то между ними образуется просвет (рис. 8.3а); если же обе половинки находятся в одной системе отсчета — просвета не возникает (рис. 8.3б). Парадокс стал возможен потому, что каждый кусок линейки вправе иметь свою собственную систему отсчета, иначе мы не могли бы их транспортировать по отдельности (рис. 8.2 а и б), поэтому использование двух координатных систем (рис. 8.3а) оправдано.
Однако нет большого смысла в том, чтобы вводить две системы отсчета для частей, движущихся с абсолютно одинаковыми скоростями: ведь можно обойтись и одной-единственной системой координат, начало которой, например, связать с левым торцом левого куска. Отсюда случай, представленный рис. 8.3б, и, соответственно, рис. 8.2д, не менее логичен.
Наконец, можно было бы выбрать две системы отсчета, для каждого куска свою собственную, но нули координатных систем совместить так, как это показано на рис. 8.3в. В данном случае просвет также отсутствует, но расположение кусков линейки на 7 часов по неподвижным часам будет отличаться от расположения, показанного на рис. 8.3б. Очевидно также, что могут быть и другие варианты.
Рис. 8.3. Разъяснения к парадоксу распиленной линейки. Случай (а) соответствует варианту (в) на рис. 8.2, когда каждый кусок линейки связан со своей собственной системой отсчета. Случай (б) соответствует варианту (д) на рис. 8.2, когда оба куска линейки связаны одной системой координат. Случай (в) демонстрирует совершенно иное, чем у случая (а), расположение координатных осей. Какую систему координат выбрать для наших кусков линейки, в действительности, дело вкуса каждого человека.
Парадокс распиленной линейки имеет некоторое сходство с противоречием, которое должно было бы возникнуть в физике древних. Действительно, Аристотель считал, что из двух предметов, брошенных с высоты вниз, упадет быстрее тот, который тяжелее. Галилей на опыте доказал ограниченность такого взгляда на вещи. Как бы мог рассуждать Галилей перед тем, как подняться на Пизанскую башню?
Пусть с Пизанской башни брошено вниз целое пушечное ядро. Чем этот случай будет отличаться от случая, когда ядро распилено пополам? Ведь пушечное ядро «не знает», что оно распилено. Разве куску чугуна одной половины ядра не все равно, летит или не летит рядом с ним кусок чугуна другой половины? И если оба куска чугуна плотно сцеплены друг с другом, какое влияние это может оказать на быстроту падения? Почему отдельные куски пушечного ядра должны лететь медленнее, чем те же самые куски, но сложенные в одно целое?
Парадокс, возникший в рамках физики Аристотеля относительно падения отдельных кусков и целого ядра, имеет ту же логическую основу, что и парадокс, возникший в физике Эйнштейна относительно сокращения отдельных кусков распиленной и не распиленной линейки при их движении с субсветовой скоростью. В обоих случаях закон физики, индифферентный к целостности объекта, дает различные результаты в зависимости от того, будем ли мы последовательно применять его к отдельным частям объекта, чтобы затем сделать вывод об объекте как целом, или же, напротив, применим его сначала к целому объекту с тем, чтобы потом сделать заключение о состоянии его отдельных частей. Возможно, именно неодинаковость результатов абсолютно равноправных логических цепей — от частей к целому и от целого к частям — заставили Галилея в свое время пересмотреть основания аристотелевской физики. Во всяком случае, эта причина должна побудить нас более внимательно отнестись к основаниям релятивистской физики.
* * *
Равноправие вариантов, изображенных на рис. 8.3 б и в, вынуждает нас несколько иначе взглянуть на парадокс с лампочкой. Дело в том, что укороченный проводящий стержень А на рис. 8.1в может занять любое положение относительно бруска В. Поясним эту мысль рис. 8.4, где показаны отдельные фазы мысленного эксперимента, проводимого уже с одной линейкой, длина которой регистрируется двумя лучами света, направленными на концы линейки; напротив источников света 1 установлены фотодатчики 2.
Рис. 8.4. В парадоксе с распиленной линейкой проявляется эффект, который можно было бы назвать дрейфом нуля системы отсчета, Пусть покоящийся стержень имеет такую длину, которую едва бы хватило для закрытия фотодатчиков 2 от лучей источников света 1 (а). Тогда при движении стержня мы будем иметь различное положение сокращенного стержня: все будет зависеть от положения нулевой отметки системы координат, связанной с нашим стержнем. Поэтому на определенный момент времени может получиться так, что окажется закрытым левый фотодатчик (б), правый (в) или оба датчика окажутся освещенными источниками света (г).
Если стержень покоится, то оба датчика окажутся затемненными, как это показано на рис. 8.4а. Теперь заставим линейку двигаться мимо фиксированных лучей со скоростью, близкой к скорости света. С точки зрения Галилея, обязательно наступит такой момент, когда оба фотодатчика окажутся закрытыми от лучей, так как линейка при своем движении не изменит своей длины. Предположим, что это произойдет в 7 часов по часам, расположенным в неподвижной системе отсчета. Какое положение в это время займет линейка согласно теории Эйнштейна, мы сказать не сможем: будет ли ровно в 7 часов затемнен левый датчик (рис. 8.4б), правый (рис. 8.4в) или же сокращенная линейка окажется где-нибудь в промежутке между лучами света (рис. 8.4г). Может случиться, что мы вообще не сможем показать сокращенную линейку, поскольку субъекту теории взбредет в голову отнести начало движущейся системы координат на километр от линейки. Здесь все зависит от того, в какую точку необъятного пространства мы поместим начало координат.
Рис. 8.4 демонстрирует, что парадокс распиленной линейки проистекает не только от множественности систем отсчета, но и от выбора нуля в движущейся координатной системе. Выбор начала координат делается субъектом теории самым произвольным образом и не диктуется объективной реальностью. Отсюда возникает неопределенность в расположении сокращенного стержня. Рис. 8.4б соответствует случаю, когда нуль системы отсчета находится на левом конце линейки, рис. 8.4в — на правом ее конце, а рис. 8.4г отражает случай, когда нуль близок к середине стержня — все три случая абсолютно равноправны. Какая картина будет наблюдаться на самом деле, никто вам сказать не сможет.
Таким образом, парадокс, связанный с сокращением длины, трансформируется в парадокс дрейфа нуля. Роль нуля в движущейся и одновременно сокращающейся системе отсчета является исключительно важной. Проиллюстрируем этот факт следующей простой и наглядной моделью.
Представим себе растянутый резиновый жгут с метками через равные отрезки длины. Отпустим левый конец жгута, закрепив предварительно правый . Все отрезки длины между двумя соседними метками сократятся и сместятся вправо, причем каждый на свою величину. Если принять за нуль левый конец жгута, зажав его, например в тисках, то картина изменится на противоположную. При отпускании правого конца растянутого жгута все размеченные отрезки сократятся, и переместятся влево. Поскольку в обоих случаях отрезки преодолевают различные расстояния, то, следовательно, их скорость перемещения по направлению к зажатому концу будет различной.
Ситуация становится еще более неопределенной в СТО, где имеет место движение предметов вдоль бесконечных координатных осей. Тогда вместе с безграничной неопределенностью нулевой точкой появляется безграничная неопределенность в расположении сокращенных и быстро перемещающихся стержней (или любых других предметов), а также безграничная неопределенность в скорости их перемещения. Таким образом, у нас возникают серьезные основания для сомнений в отношении параметра v, который фигурирует в преобразованиях Лоренца. Можно ли его трактовать как скорость продольного перемещения одной координатной системы относительно другой? Если в системе отсчета наблюдается сокращение длины, то такая интерпретация параметра v будет порождать неопределенность.
* * *
Пример с сокращением резинового жгута наводит нас на мысль, что преобразования Лоренца (или гиперболические преобразования) не могут участвовать в продольном перемещении. Действительно, изменения масштабных единиц при не ортогональном повороте штрихованной системы связано с группой симметрии вращения, а при перемещении предметов вдоль прямых имеет место группа симметрии продольного перемещения. Эти две формы движения несовместимы, т.е. преобразования Лоренца в принципе не могут отражать поступательное движение штрихованной системы K'(x', ct') относительно не штрихованной K(x, ct). Их поступательное движение может быть отражено только преобразованиями координат по Галилею, аналитический вид которых всем хорошо известен. Если помнить, что β = v/c, то эти классические преобразования записываются слеующим образом:
x = x' + βct' , ct = ct'; x' = x – βct, ct' = ct.
Продольное движение штрихованной системы K'(x', ct' ) вдоль оси абсцисс покоящейся не штрихованной системы K(x, ct) показано на рис. 8.5. Величины x, x', ct, ct', фигурирующие в преобразованиях Галилея, являются координатами точки A в системах K(x, ct) и K'(x', ct' ).
Рис. 8.5. Продольное перемещение координатной системы K' относительно системы K, что соответствует преобразованиям Галилея.
Внимательно взгляните на рис. 8.5, где изображено поступательное движение координатной системы, а затем на диаграмму Минковского, где изображено вращательное движение координатных осей, и спросите себя, как так могло получиться, что вращательное движение осей, описываемое формулами преобразования Лоренца —
,
;
,
.
— перешло в поступательно движение этих осей, описываемое формулами преобразования Галилея? Каким таким предельным переходом можно заставить изменить симметрию движения с вращательного характера на поступательное?
Как только будут заданы эти вопросы, тотчас станет понятна еще одна грубейшая математическая ошибка, допущенная отцами-основателями теории относительности. Предельный переход, выраженный формулой β = v/c → 0, никогда не приведет от формул преобразования Лоренца к формулам преобразования Галилея. Если выполняется условие v << c, то гиперболический поворот осей оказывается ничтожно малым, т.е. x » x', ct » ct', но это вовсе не означает, что координатные оси системы K' продольно переместятся вдоль оси x системы K. Другими словами, условие v/c → 0 никогда не приведет к формулам Галилея:
x = x' + vt' , x' = x – vt , t' = t,
как учат нас релятивисты, поскольку, если в преобразованиях Лоренца оставлен без изменения числитель, то должен оставаться без изменения и знаменатель.
Таким образом, предельный переход от классической физики к релятивистской не может быть осуществлен путем предельного перехода β → 0. Ошибка такого перехода стала возможна из-за того, что гиперболические преобразования Лоренца записывали в форме:
,
;
,
.
Затем говорили, что условие v << c равносильно условию c → ∞, следовательно, преобразования Лоренца переходят в преобразования Галилея, записанные выше.Иначе говоря, скорость устремления членов +vt' и –vt к нулю в преобразованиях Лоренца будет точно такой же, как и скорость приближения радикала к единице.
Математическую некорректность рассуждений релятивистов мы выяснили путем логических рассуждений вокруг парадокса распиленной линейки или эффекта дрейфа нуля. Но к этому же выводу можно прийти, если внимательно проследить за некорректностью математических выкладок релятивистов. Ясно, что вращательное движение (преобразования Лоренца) не перейдет в продольное смещение (преобразования Галилея) за счет параметра скорости.
Изменение эталонов длины и времени происходит за счет вращения координат системы K' относительно системы K при совмещенных нулевых точках. Когда нули систем «разъезжаются» в разные стороны, масштабы координатных осей не должны изменяться. Релятивисты же обычно совмещают два типа движения: сокращение эталонов, возникающее из-за вращения осей, и продольное перемещение осей, внося тем самым невообразимую путаницу в кинематику движения материальных тел. Неопределенность в положении сокращенных отрезков, изображенных на рис. 8.2 — 8.4, является результатом как раз этой «отвязки» нулей.
* * *
Сокращение длины приводит к разбалансировке уравновешенных механических систем. В релятивистской механике доказывается, что компонента Fx вектора силы в направлении движения системы отсчета не меняются, зато две других компоненты — Fy и Fz, — перпендикулярные направлению движения, уменьшаться в
раз:
F'x = Fx, F'y = Fy
Теперь представьте себе самый простейший механизм – изогнутый под прямым углом уравновешенный в системе K двумя силами Fx и Fy рычаг (рис. 8.6а). Наблюдатель движущейся системы K' зарегистрирует нарушение равновесия (рис. 8.6б), которое произойдет за счет сокращения длины продольного плеча l'x и уменьшения поперечного компонента силы F'y. Следовательно, наблюдатель системы K' должен наблюдать поворот рычага под действие момента M = – β2Fxly. Ни о какой эквивалентности движущейся и покоящейся систем отсчета говорить нельзя: налицо вопиющее противоречие.
Один наш знакомый релятивист написал об этом парадоксе так: «Весьма остроумное разрешение этого парадокса принадлежит Лауэ... В системе K рычаг движется, и в единицу времени сила Fx совершает работу – Fxv. Сила Fy не совершает работы, так как она направлена нормально к скорости рычага. Следовательно, на конце рычага, в точке приложения силы Fx, совершается работа, и в единицу времени энергия рычага в этой точке возрастает на величину – Fxv. Но это означает, что масса рычага в точке приложения силы в единицу времени возрастает на – Fxv/c2. Умножив эту величину на скорость рычага v, найдем приращение импульса – β2Fx . А момент импульса за единицу времени возрастет на – β2Fxly. А это как раз и есть дополнительный момент» [1, с. 282].
Объяснение Угарова не выдерживает никакой критики; он не устраняет проблемы, а только преумножает их. Откуда взялась «единица времени»; по каким часам она измеряется? Почему нужно говорить о «работе», а не о мощности? Но пусть останется работа: все равно сила Fx никакой «работы» совершать не может.
Действительно, предположим, вы съезжаете с горы на лыжах со скоростью v мимо мальчика, который, поднимаясь в гору, везет за собой санки; при этом он прикладывает к ним силу F. Оттого, что вы проехали мимо со скоростью v, мальчик не устанет больше на величину пропорциональную Fv и его масса не увеличиться на m = Fv/c2. И что означают слова «масса рычага в точке приложения силы»? Центр тяжести рычага может быть сосредоточена где угодно; масса же вообще здесь не должна участвовать.
Но пусть она участвует; тогда почему для нее взята формула: E = mc2, а не m0/
Теперь вообразите себе, что силы Fx и Fy действуют в системе K периодически, т.е. одновременно то включаются, то выключаются. В системе K' эта одновременность выполняться уже не будет, например, сила Fx выключится, в то время как сила Fy будет еще действовать, следовательно, для движущегося наблюдателя действующая сила Fy окажется не скомпенсированной и это также приведет к повороту рычага.
Рис. 8.6. Парадокс рычага. Сокращение длины и различное влияние скорости движения vx механической системы на изменения составляющих вектора силы приведет к тому, что первоначально уравновешенная механическая система (а) придет в неравновесное состояние, когда система будет равномерно и прямолинейно перемещаться вблизи покоящегося наблюдателя (б). Если такая разбалансировка происходит с простейшим механизмом, каковым является рычаг, то, что будет с более сложными механизмами?
Парадокс рычага известен с момента возникновения теории относительности. Его рассматривали, в частности, Льюис и Толмэн, которые в 1909 г. написали: «... Для того чтобы удержать рычаг в равновесии, сила Fx должна быть меньше силы Fy во столько же раз. Таким образом, мы видим, что в движущейся системе единица силы, движущаяся в продольном направлении меньше поперечной единицы в
* * *
Точно таким же спекулятивным способом, далеким от истинной физики и математики, Угаров объясняет другой парадокс.
Пусть в квадратной раме на резиновых растяжках висит гантель, которая в системе K уравновешивается силами F1 и F2 (рис. 8.7а). Наблюдатель движущейся системы K' должен будет зарегистрировать уже прямоугольник, в котором векторы силы за счет уменьшения их вертикальных составляющих отклонятся от диагональной линии растяжек (рис. 8.7б). Объяснение этого парадокса заняло у автора три страницы текста и математических выкладок. Не станем утомлять читателя их подробным разбором, приведем его итоговую фразу: «...Парадокс разрешается просто [!]: в релятивистской динамике ускорение, вообще говоря, не совпадает по направлению с действующей силой [?] и, хотя силы направлены под углом к направлению нити, ускорение направлено вдоль нити [?]» [1, с. 280].
Рис. 8.7. Парадокс с гантелью на растяжках. В состоянии покоя F1 и F2 уравновешивают гантель (а). В случае движения этой механической системы происходит разбалансировка сил: векторы F1 и F2 отклонятся от направления, заданного резиновыми жгутами, которыми удерживается гантель (б). Во-первых, допустимо ли, чтобы сила упругости жгута действовала под углом к нему? Во-вторых, в этой системе, как и в системе с рычагом, нарушается принцип эквивалентности движущейся и покоящейся систем.
Угаров забыл первую заповедь своего учителя о неизменности физических законов для движущихся и покоящихся систем. Сколько усилий релятивистами было затрачено, чтобы вывести одинаковыми уравнения Максвелла для систем К и К', а теперь, пожалуйста, в системе К' возникли «особенности»: между вектором ускорения и вектором силы появился угол. Как это можно себе представить: ускорение направлено в одну сторону, а сила, его вызвавшая, — в другую? Почему гантель должна реагировать на направление именно ускорения и проигнорировать направление действия силы?
В парадоксе с гантелью, как и в парадоксе с рычагом, а также в парадоксе с часами и лампочкой, возникла асимметрия. Релятивисты говорят, что эта асимметрия только кажущаяся, так как, с точки зрения противоположного наблюдателя, его асимметрия окажется противоположного характера. Хорошо, пусть так, тогда почему релятивисты требуют полного совпадения волнового уравнения и уравнений Максвелла для штрихованной и не штрихованной систем координат? Как так получается, что в электродинамики почему-то добиваются неизменного вида формул для движущейся и покоящейся систем отсчета, в для механики к этой неизменности даже не стремятся? Релятивисты потратили тысячи тонн бумаги и офсетной краски, чтобы отпечатать миллионными тиражами книги и учебники по релятивистской механике, согласно которой наш мир не мог бы просуществовать и доли секунды. Мосты, арки, купола и другие инженерные сооружения, рассчитанные по законам классической механики, должны будут рассыпаться с точки зрения наблюдателя, движущегося с субсветовой скоростью.
В самом деле, если движение осуществляется вдоль оси x, то все параллельные этой оси отрезки должны будут сократиться, а компоненты силы Fx останутся неизменными. И, наоборот, отрезки, параллельные осям y и z, останутся неизменными, а силы Fy и Fz уменьшаться. Все это, с точки зрения движущегося наблюдателя, приведет к разбалансировке внутренних напряжений в конструкциях и они придут в негодность или потеряют прежнюю надежность. Из-за сокращения длины произойдет перераспределение центра масс, что также повлечет за собой катастрофические последствия даже для самых простейших механизмов. Релятивисты тщатся как-то оправдаться, например, так: «В теории относительности понятие центра масс сложнее и не обладает столь же отчетливым физическим смыслом, как в нерелятивистской теории. Причина этого заключается в том, что в релятивистской физике нет универсального "центра масс" как точки, которая не зависела бы от выбора системы отсчета» [3, с. 106].
Однако инженерам не станет легче от подобного разъяснения. Им должно быть понятно одно: по формулам теории относительности нельзя рассчитать ни одной механической конструкции, начиная с самой простейшей — рычага. Таким образом, релятивистская механика — это громоздкая, страшно запутанная система бессмысленных символов, которым ее создатели присвоили различные имена: «энергия», «импульс», «ускорение» и т.д. Но их спекулятивная наука имеет исключительно формалистское значение, она не применима к действительному миру вещей. Есть несколько формул (например, E = mc2), которые работают в реальной физике, однако, никакого «релятивистского» содержания они не несут. Это — случайные совпадения, вроде формул, описывающих доплер-эффект, с ними нужно разбираться отдельно. В целом же на принципах теории относительности невозможно возвести какого-то прочного, непротиворечивого здания науки о механизмах.
* * *
Если кто-то подумал: «Бог с ней, с механикой инженерных конструкций, зато специальная теория относительности облагодетельствовала электродинамику движущихся тел», значит, он плохо знает релятивистскую механику и электродинамику. Этот бедолага и шага не сделает в области электродинамик движущихся тел, как тут же споткнется о противоречия. Вот одно из них, которое так же элементарно для электродинамики, как нарушение равновесия рычага для механики.
Пусть два одноименно заряженных тела через изоляторы связаны между собой пружиной. Для наблюдателя А, находящегося в системе отсчета заряженных тел, сила растяжения пружины будет равна FA, которую он может зафиксировать, например, по стрелке динамометра. Для наблюдателя В, движущегося относительно А с некоторой скоростью v (причем не обязательно сопоставимой со скоростью света с), сила взаимодействия должна быть иной, обозначим ее через FB. Это связано с тем, что движущиеся заряды индуцируют вокруг себя магнитное поле, которое изменит силу FA. Следовательно, тот же самый прибор для наблюдателя В должен показать другое значение силы, так как для этого наблюдателя заряды будут находиться в движении.
Мы не сможем избавиться от этого противоречия, если не откажемся от принципа относительности в электродинамике. Скорость заряженного тела v есть величина абсолютная и она должна измеряться по отношению к покоящемуся эфиру, только в этом случае наблюдатели A и B будут фиксировать одну и ту же силу взаимодействия между телами (FA = FB).
Принцип относительности, он же первый постулат, гласящий: «все законы природы, справедливые в покоящейся системе, будут справедливыми и в движущейся системе», нарушался всегда и везде, стоило нам сделать по одному шагу в сторону механики и электродинамики. «Почему это произошло?» — спросит читатель. — «Да потому, что противоречие заложено в ее толковании пространства и времени», — ответим мы. — «Тогда почему известен только парадокс часов и почти не известно о других противоречиях?» — «Да потому, что парадокс часов слишком понятен для широкой публики, а парадоксы, выстроенные на механических и электромагнитных конструкциях, будут понятны только специалистам». — «Тогда почему молчат специалисты?» — «Да потому, что им всем противно копаться в мусорной куче, которая называется теорией относительности. Это такая клоака, что для всякого конструктивно мыслящего человека погружение в нее окажется хуже пытки каленым железом. Вы можете убить целый вечер, разбирая одну страницу их бредней. И вот, когда, наконец, вы поняли ошибочность текста этой страницы и перевернули ее, чтобы начать читать следующую, вас ожидает новая порция спекуляций, и так на протяжении чтения всей книги».
|
|
|
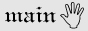
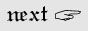
