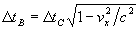Критика теории относительности
О.Е. Акимов
9. Парадоксы времени
В работе 1905 года Эйнштейн написал: «часы с балансиром, находящиеся на земном экваторе, должны идти несколько медленнее, чем точно такие же часы, помещенные на полюсе, но в остальном поставленные в одинаковые условия» [4,т. 1, с. 20]. Здесь автором была допущена очевидная ошибка: часы на полюсе и на экваторе относительно друг друга никуда не перемещаются, так как находятся на одной и той же жесткой поверхности. Мы имеем дело с одной вращающейся системой координат, в которой находятся пара неподвижных часов.
Обманчивое впечатление о движении часов на экваторе относительно часов на полюсе возникло у Эйнштейна потому, что всякий человек как метанаблюдатель склонен занимать позицию стороннего наблюдателя в абсолютной системе отсчета. Однако в данной ситуации метанаблюдателю лучше всего расположиться на экваторе и смотреть вдоль меридиана на объектного наблюдателя, стоящего на полюсе. Положение этих двух наблюдателей можно сравнить с двумя спортсменами, крепко привязанными (чтобы не смыло волной) к своим местам в двухместном каноэ, которое горный поток бросает из стороны в сторону, и оно время от времени попадает в бурные водовороты.
Непредвзято мыслящему читателю ясно, что Эйнштейн плохо продумал данный пример для иллюстрации эффекта замедления времени, который к тому же имел более серьезные последствия. Я имею в виду парадокс часов. Когда отец-основатель релятивизма там же написал: «...Если в A находятся двое синхронно идущих часов и мы перемещаем одни из них по замкнутой кривой с постоянной скоростью до тех пор, пока они не вернуться в A, на что потребуется, скажем, t сек., то эти часы по прибытию в A будут отставать по сравнению с оставшимися неподвижно часами на t(v/V)2 сек.», мы понимаем, что он вновь поторопился с выводом. Стоило ему еще чуть-чуть подумать и он сам бы сообразил, что сказал нелепость, так как его же первый постулат требует от хода обоих часов полной взаимности.
Это, как было сказано, — исключительно логическое противоречие, но в нем можно выделить и количественный компонент. Предположим, существует третий наблюдатель C, перемещающийся относительно и A, и B. Если мы будем подсчитывать разницу во времени относительно только двух наблюдателей — A и B, получим одну разницу в их возрасте; если же мы посчитаем разницу в возрасте этих двух наблюдателей, учитывая третьего — C, то получим другое число. То есть расчет по схеме AB количественно отличается от расчета АCB. Критики СТО спрашивают релятивистов: а почему, собственно, присутствие третьего лица должно влиять на разницу в возрасте A и B? Но не станем усложнять себе задачу третьим наблюдателем и пока рассмотрим классический парадокс двух близнецов.
Итак, никакого отставания движущихся часов от покоящихся быть не должно, поскольку, с точки зрения движущегося вместе с часами наблюдателя, ситуация выглядит ровно наоборот, и тогда уже «покоящиеся» часы должны будут отстать от «движущихся». В данном случае Эйнштейн как метанаблюдатель поместил себя в координатную систему движущихся часов и совершенно выпустил из виду вторую, «покоящуюся» систему отсчета. Такая инерционность мышления вполне понятна. Она свойственна людям формалистского склада ума, которые не хотят или не умеют комбинировать пространственными образами. Релятивисты не мыслят конструктивными представлениями и придерживаются той нехитрой модели, которая явилась перед их внутренним взором первой.
Тогда, в далеком 1905 году, все еще можно было поправить, если бы рядом с Эйнштейном находился человек с более конструктивным мышлением, чем у него. Пускай бы и появились злосчастные преобразования Лоренца, но конструктивно думающий человек мог бы подсказать автору теории относительности, как не надо интерпретировать их. Сегодня исправлять ошибки поздио: любая глупость, случайно сорвавшаяся с языка великого гуру, должна получить рациональное объяснение. Уже к началу Второй мировой войны теория относительности господствовала повсеместно: «... К этому времени все уже были настолько интеллектуально непроницаемы для любых соображений, представляющих угрозу открытию Эйнштейна, и той картине мира, которая им определялась, что еще раз начинать мыслить по-новому было уже невозможно» [5, с. 33].
Мы все находимся под глубоким гипнозом обаятельной личности Эйнштейна. Его скромность околдовала нас: «Вам кажется, что я взираю на труд моей жизни со спокойным удовлетворением. Вблизи все это выглядит иначе. Нет ни одного понятия, в устойчивости которого я был бы убежден. Я не уверен вообще, что нахожусь на правильном пути. Современники видят во мне еретика и реакционера, который, так сказать, пережил самого себя. Все это, конечно, вопрос моды и объясняется их недомыслием. Но чувство неудовлетворенности поднимается во мне и изнутри. Впрочем, иначе и быть не может, если ты критически относишься к себе» [6].
Вспоминаются слова Эйнштейна, которые он произнес под вечер своей жизни: «Не моя вина, что читатели получают преувеличенное представление о важности достигнутых мной результатов. В этом скорее повинны авторы популярных статей и в особенности корреспонденты газет, которые преподносят все, как нельзя сенсационней» [7, c. 70]. Мы парализованы огромным авторитетом десятка других выдающихся физиков мира. Нужно обладать изрядной долей самомнения, чтобы посягнуть на святыню сотен университетов и бесчисленного множества почитателей Эйнштейна, для которых теория относительности, что Библия для христианина. Однако, если обратиться к истокам этой доктрины, непосредственно к ее основаниям, то обнаружится масса обидных ошибок, откровенных промахов и намеренных натяжек.
Все без исключения «решения» парадокса близнецов, предложенные релятивистами, строятся на нарушении ими в той или иной форме первого постулата СТО о тотальной симметричности кинематической ситуации. Таким образом, антирелятивисту остается лишь внимательно следить за ходом рассуждения релятивиста и фиксировать, в каком месте своих рассуждений тот наступит на горло своей теории и нарушит принцип относительности движения.
Сначала все нарушения симметрии релятивисты оправдывали ускорением. Так поступал сам Эйнштейн, а за ним Паули, Борн и др. В этом случае проблема выводилась из сферы СТО в сферу ОТО. Но затем релятивисты согласились с теми простыми доводами антирелятивистов, которые предлагали тем или иным способом нейтрализовать любые эффекты, вызванные ускорением. Противники учения Эйнштейна говорили: пусть брат-космонавт испытает какие-то ускорения, тогда заставьте брата-домоседа испытать все те же ускорения на земле и проблема будет снята.
После того, как ускорение забраковали в качестве решающего аргумента, был изобретен так называемый радиолокационный метод, когда наблюдатели обмениваются световыми сигналами и свои вывода делают с учетом эффекта Доплера. Этот метод возник вскоре после смерти Эйнштейна, когда проблему парадокса времени с новой силой поднял президент Королевского астрономического общества Дингл. Одновременно лорд Холсбэри предложил схему трех братьев-близнецов, которая автоматически исключала фактор ускорения. Таким образом, в руках релятивистов оказался очень гибкий (правильнее сказать, более спекулятивный) инструмент, в соответствии с которым бег времени отождествлялся с периодом электромагнитных колебаний, который, согласно формулам Доплера, можно легко заставить убыстряться или замедляться.
Однако каждому здравомыслящему человеку отлично известно, что собственная частота биения сердца не зависит от того, перемещается человек в пространстве или нет, хотя воспринимаемая частота пульса за счет эффекта Доплера может гулять довольно в широких пределах. Поэтому увязывание этого эффекта со старением организма является грубой ошибкой. Тем не менее, релятивисты отождествили обратимые физические явления с необратимыми биологическими и в результате на свет появились десятки различных схем хода лучей, которыми обменивались наблюдатели, которые «молодели» или «старели» в зависимости от частоты воспринимаемых сигналов. Но независимо от сложности хода лучей, которые вычерчиваются релятивистами в рамках радиолокационного метода, их ошибка по-прежнему состоит в одном: в нарушении условия симметрии кинематической ситуации.
Релятивисты не владеют своим воображением настолько, чтобы представить ситуацию с позиции подвижного наблюдателя. Они не понимают, что вычерчивание мировых линий, диаграмм Минковского и прочих схем можно как с точки зрения «штрихованного» наблюдателя, так и «нештрихованного» — рисунки их совпадут. Следовательно, все рассуждения, относящиеся к, условно говоря, «покоящемуся» наблюдателю A, в полной мере относятся к «движущемуся» наблюдателю B. Ракета с летящим братом-близнецом удаляется от неподвижного брата-близнеца точно так же, как удаляется земля с «неподвижным» братом-близнецом от ракеты. При этом необходимо твердо помнить, что абсолютная система координат в СТО отсутствует и нужно всячески пресекать попытки ее введения.
Руководствуясь правилом абсолютной симметрии двух систем отсчета, о которых невозможно определенно сказать, движутся они или покоятся, нетрудно найти логические ошибки в рассуждениях релятивистов. Так, например, если релятивист написал, что пространство, несущееся навстречу брата-близнеца A "укоротилось" в n раз, то аналогичная фраза и соответствующая формула должны фигурировать для брата-близнеца B. Отсутствие такой фразы и формулы релятивисты могут оправдывать как угодно, в частности, введением неподвижной точки в своем внутреннем психологическом пространстве. Однако при этом, через свое субъективное пространство они нарушают главный принцип СТО.
Из предыдущих разделов нам стало ясно, что переход от четырех переменных x, y, z, t к четырем другим переменным x', y', z', t' и, который называется «преобразованиями Лоренца», не отвечает преобразованиям координат двух быстро движущихся относительно друг друга систем отсчета. Никакого реального или даже кажущегося замедления времени и сокращения длины не существует. В это можно продолжать верить, истолковывая по-своему результаты некоторых физических опытов, но этого нельзя доказать математически.
Когда вы читаете текст, например такого содержания: «Исследователь, движущийся вместе с лабораторией, сам состоит также из атомов. Значит, и его тело должно укоротиться во столько же раз, во сколько укоротятся его линейки, так что он не заметит какого-либо изменения. Подобным же образом все физико-химические процессы, протекающие в нем самом, замедлятся во столько же раз, во сколько замедляются его часы. По-видимому, мыслительные процессы этого исследователя также замедлят свой ход, и он не почувствует изменения скорости хода своих часов. Поэтому он будет приписывать своим линейкам ту же длину, которой они обладали, когда покоились относительно эфира, и тот же период своим часам. Все это необходимо учитывать при истолковании его экспериментальных результатов» [3, с. 44], — знайте, вы читаете чепуху, вас откровенно водят за нос.
Тот, кто говорит вам, что от быстрого перемещения в пространстве тормозятся умственные процессы и люди начинают плохо соображать на счет своих линеек и часов, — не исследователь природы, а мошенник от науки. Он может быть известным, даже очень знаменитым человеком, только вся его слава пришла к нему от его подельников, таких же, как он, мошенников. Весь XX век наполнен горячими дискуссиями о пространственно-временной структуре Вселенной, которые больше походили на споры средневековых схоластов об акциденции Бога. Вопреки первой заповеди познающего: вещи разумны по своей природе, не пытайся в этот мир привнести свой разум, нынешний физик уподобляется индийскому Брахме, ткущему из самого себя паутину мировых законов. Нередко можно слышать, как физики делают упрек философам, будто бы те все свои проблемы «высасывают из пальца». Это может быть и так, только не физикам об этом судить, чтобы делать подобные замечания, надо быть самим в этом отношении безупречными.
* * *
Все нерелятивисты знают, что проблема часов в теории относительности неразрешима. Однако релятивисты или люди, благосклонно к ним относящиеся, не перестают предлагать всё новые и новые «решения». Для них явно недостаточны те общеметодологические доводы, которые приводят антирелятивисты. Именно для таких людей мы предприняли настоящий анализ одного из самых известных парадоксов, каковым является парадокс часов.
В 20-е и 30-е годы ХХ века физика была на подъеме, огромная армия писателей во всем мире сочиняла бесчисленные романы об увлекательных путешествиях во времени, и только небольшое темное пятнышко омрачало эту радужную перспективу. Этим пятнышком был нерешенный парадокс часов. Сразу же после создания специальной теории относительности появилось несколько предложений по решению проблемы времени. И хотя варианты, предложенные Паули, Рейхенбахом, другими авторитетными учеными, включая Эйнштейна, между собой сильно различались, проблема на три-четыре десятка лет была снята.
Однако после смерти Эйнштейна Дингл вновь неожиданно поднял вопрос о парадоксе часов. Ряд физиков (Холсбэри, Бом, Борн и Бонди), желая убедить его в том, что никакого парадокса не существует, сформулировали новую методику геометрической интерпретации основных выводов специальной теории относительности, который называется методом коэффициента k. В нашей стране в 60-х годах также активизировалась работа по разрешению парадокса часов. В.А. Фок, Д.В. Скобельцын, И.И. Гольденблат, Я.П. Терлецкий и многие другие физики на важных международных форумах, в периодической печати и, наконец, в фундаментальных исследованиях предлагали свои варианты решения проблемы времени, в том числе связанные с радиолокационным методом.
Пережевывание этого вопроса на протяжении более чем двух десятков лет порядком утомило научное сообщество. Сегодня поднимать эту проблему вновь считается признаком научного невежества. На всякий неожиданно раздавшийся вопрос: «Какой из близнецов состарится скорее: тот, что летит в ракете, или тот, что остался на Земле?» релятивисты стали раздраженно отвечать вопросом: «Существует добрая сотня способов доказательства того, что неравенство А < В нисколько не противоречит неравенству А> В. Вам этого мало?»
Действительно, на сегодняшний день имеется масса самых разнообразных решений парадокса часов, которые совершенно невозможно согласовать между собой. В этом, как мы указали выше, проявляется концептуальный релятивизм теории относительности, который можно выразить примерно следующей фразой: «Каждый ученый в своем кабинете всегда сочиняет истинную теорию, а всякий другой ученый по отношению к первому всегда окажется не прав». Перед анализом нескольких предлагаемых решений парадокса часов еще раз напомним суть проблемы.
Согласно представлениям классической физики абсолютное пространство трехмерно, а абсолютное время одномерно или однонаправлено. Оно равномерно течет от прошлого (отрицательное время) через настоящее (его удобно совмещать с нулевой отметкой) к будущему (соответствует положительной части стрелы времени). Наиважнейшей характеристикой времени является его необратимость: человек может переместиться на 6 километров на запад, а потом на 6 километров на восток, но он не может на 6 лет состариться, а потом по своему желанию на 6 лет помолодеть. Это свойство времени делает эйнштейновский принцип относительности невозможным в самом элементарном случае.
Для построения парадоксов длины требуется затратить несколько больше интеллектуальных усилий. Хотя мы указали еще на ряд парадоксов, которые говорят нам о противоречивости релятивистской догмы. Если концепция дает сбой в одном месте, то можете быть уверены, что она подведет вас в любом другом месте. Таким образом, все выводы теории относительности легко перечеркиваются одним противоречием, которое воссоздано в парадоксе часов или парадоксе двух братьев-близнецов. Если один брат-близнец (А) остался на Земле, а другой (В) улетел с большой скоростью на ракете в космическое путешествие, то брат-путешественник, согласно утверждению о замедлении времени в движущейся системе, состарится меньше, чем брат-домосед (А > В). Принцип относительного движения заставляет считать нас движущимся брата-домоседа относительно брата-путешественника, и тогда уже путешественник состарится скорее, чем домосед (А < В). При встрече братья-близнецы могут прийти только к одному-единственному правильному выводу: теория относительности абсурдна.
* * *
Анализ этого парадокса часов мы начнем с рассмотрения доводов Дингла.
Герберт Дингл, профессор естественной философии Имперского колледжа наук и технологии с 1937 по 1946 гг., профессор истории и философии наук Университетского колледжа в Лондоне, президент Королевского астрономического общества с 1946 по 1955 гт. свои аргументы против замедления времени изложил в трех пунктах:
«1. Согласно постулату относительности, при разобщении и последующем воссоединении двух объектов, например двух одинаковых часов, не может иметь место никакой наблюдаемый эффект, который показал бы абсолютным образом, что тот или иной объект двигался.
2. Если после воссоединения одни часы отстанут на интервал времени, зависящий от их относительного движения, а другие не отстанут, то это явление будет свидетельством того, что двигались лишь эти первые часы.
3. Итак, если постулат относительности верен, как те, так и другие часы должны отстать в равной мере или не отстать вовсе; в любом случае их показания должны быть одинаковыми при воссоединении, если они были одинаковыми при разобщении» [8, c. 130].
Самым весомым из перечисленных аргументов является тот, что предшествует этим трем пунктам, т.е. та короткая биографическая справка, которую мы предпослали аргументам Дингла. Он — ученый с мировым именем и с ним необходимо было считаться. Что касается перечисленных аргументов, то они мало чем отличаются от традиционных доводов, которые постоянно звучат в связи с бесконечным пересказом содержания парадокса: прилетел брат-космонавт из далекого космического путешествия и застал брата-домоседа глубоким стариком. Вопрос: как быть с принципом относительности?
Дингл решительно отверг доводы классиков релятивисткой доктрины (Эйнштейна, Паули, Борна и др.), которые в качестве асимметрии времени назвали ускорение. Ускорение можно исключить, говорил он, ссылаясь на схему лорда Холсбэри, в которой участвуют два брата-космонавта и один брат-домосед. Эту схему мы проанализируем позже, а сейчас добавим, что высказывания Дингла, помимо отрадного здравомыслия, отличает еще и высокая степень эмоциональности.
Например, он высказывался так: «Обнаруживается не имеющий даже аналога [в истории науки] факт, что выдающиеся физики, занимающие высокое положение в университетах и исследовательских лабораториях, до такой степени не понимают принципа относительности, что считают эти фантастические эффекты [замедление времени] его неизбежным следствием». Или еще резче: «Положение, при котором судьбы мира находятся в руках людей, оперирующих орудием, о природе которого они имеют совершенно ложное представление, — крайне опасно» [8, с. 16].
Экспрессия и даже определенная резкость в интонации никогда не повредят в деле критики релятивистов, к которым, кстати, относится и автор используемой нами сейчас книги. Его книжку, возможно, никогда бы не перевели у нас в стране и не напечатали, если бы он не отвесил низкие поклоны в сторону релятивизма, вроде: «До сих пор частная тео-рия относительности с честью проходила все проверки, и ее безоговорочно принимают за основу в тысячах расчетов каждый день в лабораториях всего мира» [8, с. 13] и т.д.
Как из навоза горох, выбираешь из книги Мардера что-нибудь съедобное, в частности: «Время жизни мезонов измерялось не непосредственно, а бьшо получено из анализа плотности и оценки количества мезонов, рождающихся на различных высотах. При знакомстве с литературой по этому вопросу (например, ...) становится, однако, ясно, что утверждаемая реальность релятивистского «замедления времени» и не подвергалась сомнению, так что толкование авторами их результатов нельзя считать совершенно непредвзятыми» [8, с. 71]. Это Мардер процитировал слова Э. Дж. Кэллуина. Но искреннего и честного с научной точки зрения материала в его книге все же крайне мало. Вообще, до обидного мало выходит серьезных исследований антирелятивистской направленности.
* * *
Итак, было сказано, что первым «решением» парадокса часов было связано с идеей ускорения. Введение его для двух равноправных систем отсчета К и К', движущихся равномерно и прямолинейно относительно друг друга, выглядит чудовищно нелогично, но релятивисты специально усложнили ситуацию с часами, чтобы за счет ускорения спасти свою теорию от неминуемого краха. Понятно, что замедление времени вытекает из преобразований Лоренца, где фигурирует только скорость v и никакого ускорения нет. И вот Эйнштейн в 1918 г., после создания им первого варианта общей теории относительности, вдруг неожиданно объявляет, что «системы координат К и К' никоим образом не являются равноправными» [11, с. 618]. Отныне движущаяся система К', прежде чем получить скорость v, должна была ускориться, и вот оно-то, это ускорение, и является якобы той самой причиной, по которой часы в системе К' после сближения с часами в системе К оказываются отставшими.
В первых формулировках Эйнштейн полностью исключал неинерциальные системы отсчета и разъяснял, почему он это сделал. Так, например, в работе 1910 г. «Принцип относительности и его следствия в современной физике» он следующим образом формулирует свой первый постулат: «Законы, управляющие явлениями природы, не зависят от состояния движения той координатной системы, относительно которой эти явления наблюдаются, если эта система не обладает ускоренным движением» [12, с. 144]. Далее у него шло примечание, где четко разъяснялось, почему ускорение необходимо исключить из теории относительности.
«Во всей этой формулировке, — пишет Эйнштейн, — мы предполагаем, что понятие ускорения обладает объективным смыслом, т.е. что наблюдатель, неизменно связанный с координатной системой, имеет возможность посредством опыта установить, обладает ли его система ускоренным движением или не обладает». В самом деле, если мы знаем ускорение, то у нас не будет никаких проблем с расчетом замедления времени, вызванного этим ускорением (если, конечно, принять, что замедление времени происходит по причине ускорения). Является ли ваша система ускоренной, несложно установить опытным путем.
Так думал Эйнштейн в 1910 году и, между прочим, очень неплохо рассуждал. Однако парадокс часов заставил его изменить эту правильную позицию на неправильную.
Что ж, согласимся, пусть ускорение добавит еще какое-то отставание часам в системе K'. Но как быть с относительным отставанием, вызванным исключительно равномерным и прямолинейным движением, которое только и ведет к парадоксу часов? Ведь было же сказано, что «часы, движущиеся относительно некоторой системы отсчета со скоростью v, идут в этой системе медленнее в отношении 1:
, чем те же часы в случае, если они покоятся относительно той же системы отсчета» [13, с.74].
Разве известная формула специальной теории относительности о замедлении времени перестала быть истинной? Нет, она по-прежнему верна. Следовательно, всем релятивистам нужно думать, как решить задачу взаимного отставания часов, а не выискивать дополнительную причину, которая бы нарушила «нерушимый» принцип относительности. Но релятивисты, в первых рядах которых оказались Паули и Борн, сделали вид, будто не поняли существа проблемы. «Замедление времени, — пишет Паули, — приводит к кажущемуся парадоксальному следствию... Решение этого парадокса заключается в том, что система K' не есть галилеева система, поэтому в ней влиянием ускорения на ход часов пренебречь нельзя» [14, с. 27 – 28].
В разделе общей теории относительности цитируемой книги Паули уточняет: «Уравнение
имеет следующий физический смысл: если одни из двух покоящихся, одинаковых и в начале синхронных часов поместить на некоторое время в гравитационное поле, то после этого оба прибора уже не идут синхронно, а напротив, побывавшие в гравитационном поле часы отстают. Как указал Эйнштейн [в работе 1918 г., ключевую фразу из которой мы привели выше], на этом основывается также объяснение ... парадокса с часами. В системе К', в которых часы U2 длительно покоятся, во время торможения имеется гравитационное поле, которое наблюдатель в K' и может считать причиной отставания покоящихся часов U2» [14, с. 221].
Читатель заметит, что приведенная Паули формула заметно отличается от формулы замедления времени, вытекающей из специальной теории относительности, так что, во-первых, ни о какой эквивалентной компенсации здесь говорить нельзя и, во-вторых, в парадоксе часов речь шла не о причинах замедления времени, а о невозможности его относительного замедления.
Борн вторит Паули в том же духе. «Однако следует заметить, — пишет он, — что связанная с В система отсчета не инерциальная. Она совпадает только в течение основного времени движения (туда и обратно) с двумя инерциальными системами отсчета. В течение отрезка времени, когда существует ускорение, в системе В появляются гравитационные поля. В начале и в конце пути А и В находятся практически в одном и том же месте пространства, и поэтому присутствующие там гравитационные поля не влияют на относительный ход часов.
Для определения разности хода часов следует принимать во внимание время действия ускорения δt при повороте. При этом из-за индуцированного гравитационного поля, которое в течение короткого промежутка времени δt можно приближенно считать постоянным в пространстве, возникает разница в показаниях часов A и B, равная (gξ/c2)δt. Легко показать, что эта разность в два раза больше отставания часов A от B, которое происходит из-за сокращения времени. Так как изменение скорости B по отношению к A за время поворота δt равно 2 v, ускорение равно g = 2v/δt. Расстояние между часами в момент поворота ξ = vt0. Следовательно, (gξ/c2) δt = 2t0v2/c2 как и утверждалось. Вычитая из последнего выражения эффект сокращения времени, находим в системе наблюдателя B ту же разность показаний часов, что и в инерциальной системе A» [15, с. 126 – 132].
Здесь существует определенная натянутость в учете времени действия ускорения, которое имеет место не только при повороте ракеты, но и во время ее разгона и торможения по прямой линии. Но вот Борн, наконец, признается в существовании противоречия, вызванного исключительно равномерным и прямолинейным движением. «... Кажется, следовало бы исходить из преобразований Лоренца» [15, с. 129], пишет он.
Не «кажется», а только так и надо понимать данную проблему. Величина замедления времени вообще не должна быть функцией ускорения g, иначе всякое изменение значения g даст отклонение от закона замедления времени, продиктованное специальной теорией относительности. Ведь ускорение g можно сделать ничтожно малым, и тогда ничтожно малым будет время отставания одних часов относительно других.
Не принимая этих очевидных аргументов, релятивисты пускаются в схоластические рассуждения: «Несмотря на то, что влиянием кратковременного ускорения часов В на их ход можно пренебречь, все же это ускорение имеет основное значение в разрешении «парадокса с часами», ибо благодаря этому ускорению изменилось направление мировой линии часов В» [10, с. 23]. Обратите внимание на это словоблудие: «можно пренебречь» и тут же «имеет основное значение». Заметим также, что «направление мировой линии» ни в какую формулу не входит.
Несмотря на очевидную нелепость: придавать решающее значение фактору ускорения и тут же пренебрегать им, такой ход мысли очень распространен у релятивистов. В связи с этим обратимся к еще одному источнику спекуляций по обсуждаемой тематике.
«Мы «сбросили со счетов» влияние кратковременных движущихся сил, воздействующих на В, — пишет видный советский релятивист Скобельцын. — Изменением показаний часов за время действия таких сил, при указанных выше условиях, всегда можно пренебречь. Не следует, однако, упускать из виду, что именно ускорение (изменение скорости часов В относительно некоторой инерциальной системы) и можно рассматривать, как причину того эффекта замедления «течения времени» в системе В (по отношению к А), которое и приводит к соотношению
. (1.13)
А именно, с точки зрения инерциальной системы А, замедление часов В вполне логично рассматривать как результат их ускорения относительно этой системы (A)» [16, с. 35].
Формулу (1.13) Скобельцын «вывел» из эффекта Доплера. Никакой логической связи между указанным эффектом и ускорением не существует. Не существует и математической связи между временем (частотой) и ускорением: если бы на замедление времени влияло ускорение g, буква g фигурировала бы и в формуле (1.13), но этого у Скобельцына нет.
Учитывая последнее обстоятельство, один из авторов, Терлецкий, формулу для замедления времени записал так [17, c. 42]:
+ δ,
уверяя всех, что δ зависит от ускорения (правда, не сказал, как δ зависит от g). Таким способом, пожалуй, к любой формуле можно приписать, что угодно, и назвать, чем угодно, только ведь второе слагаемое здесь нисколько не оправдывает действие первого слагаемого, возникающего помимо ускорения.
Мы щадим читателя и не приводим длинные и путаные рассуждения Терлецкого. Он чертит странные чертежи и просит «на глазок» сравнить реальные длины отрезков, забывая про измененные масштабы. Например, он пишет: «... Число единичных отрезков, укладывающихся на линии 0b, больше, чем число таких же, но относящихся к системе Σ' отрезков, укладывающихся на ломанной 0ab. Следовательно, часы B отстают от часов A». У него встречаются диковинные образы, например, физическое время может «скакать», подобно блохе: «... Почти мгновенно время системы Σ как бы перескочит на конечный интервал a1a2. Этот перескок не является, однако, реально наблюдаемым эффектом» и т.д.
* * *
Фантазии, фантазии и еще раз фантазии — вот та главная опора в суждениях релятивистов. Уму непостижимо, сколько миллиардов слов произнесено по всему миру в защиту тезиса о зависимости замедления времени от ускорения. Между тем этот довод об ускорении можно легко исключить, если брата-домоседа заставить испытать в земных условиях все те же перегрузки, которые испытал и брат-путешественник.
В самом деле, посадите близнецов на две одинаковые ракеты, которые, развив равные ускорения, достигнут через одинаковые промежутки времени равные скорости (рис. 9.1), только пусть затем один из братьев продолжит инерциальный полет (рис. 9.1а), а другой тут же, затормозив и развернув ракету на 180°, вернется на Землю (рис. 9.1б). Таким образом, эквивалентность фаз ускорения и торможения обоих близнецов позволит полностью исключить спекуляции на факторе ускорения.
Рис. 9.1. Ускорения и торможения брата В, отправившегося путешествовать в космос (а) всегда можно нейтрализовать, заставив брата А испытать все те же ускорения и торможения на Земле, что испытал и брат В (б).
Идея нейтрализации ускорения не пришла в голову Паули, но мысль Борна о том, что решение парадокса необходимо искать, привлекая только преобразования Лоренца, видимо, овладела им. Хитрый Паули действительно нашел весьма остроумный математический ход, жаль только, что он тоже оказался неправильным. Перескажем его идею, привлекая менее громоздкие, чем у него [10, с. 22], математические выкладки.
Паули подметил, что формуле отставания часов А от часов В —
,
соответствует прямоугольный треугольник, для которого справедлива теорема Пифагора
или
.
Затем, в последней формуле он переставляет местами два члена:
или
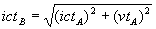
и интерпретирует эту манипуляцию символами двумя графическими диаграммами. На первой диаграмме (рис. 9.2а) покоящимся является брат B, движущимся — брат A, на второй диаграмме (рис. 9.2б) братья меняются ролями.
Рис. 9.2. Решение парадокса часов по Паули. Замедление времени брата-путешественника A представляется диаграммой (а). Но эту диаграмму можно представить по-другому — (б). В последнем случае уже путешественником будет брат В. Ошибка объяснения состоит в том, что по второй формуле замедление все же испытает брат А, который, согласно диаграмме (б), остался на Земле.
Графическое расположение мировых линий для брата А (0 — 1 — 3) и для брата В (0 — 2 — 3) внешне удовлетворяет принципу относительности: единственное, что необходимо сделать, это ввести во втором случае мнимую временную ось. Однако фокус состоит в том, чтобы объяснить совместимость исходной формулы замедления времени с принципиально иной формулой, а именно:
.
А вот этого как раз и невозможно сделать: последняя формула уже несовместима ни с первой, ни со второй диаграммами.
* * *
Теория относительности — это не гранитная плита, на которой золотыми буквами выгравированы незыблемые законы физики, каковыми являются законы Ньютона и Максвелла. Она скорее походит на городскую доску объявлений по сдаче и найму жилплощади, где непрерывно происходит замена одних объявлений другими. Мотивы, которыми руководствуются релятивисты при принятии большинства своих решений, со стороны кажутся малообоснованными и почти случайными. Сначала появляется одно объяснение, через некоторое время оно подменяется другим, проходит еще какое-то время, и это другое неожиданно сменяется третьим. Между тем книжки живут десятилетиями, поэтому первая и вторая формулы не исчезают бесследно. Какому-нибудь сельскому учителю и невдомек, что от решения парадокса часов с помощью введения ускорения, предложенного Эйнштейном, Паули, Борном, Ланжевеном и бесконечной вереницей их поклонников, «самая передовая наука» уже давным-давно отказалась и в моде объяснение на основе трех братьев-близнецов. Но наш читатель не должен слишком сокрушаться по поводу своего отставания от непрерывно поступающего потока предложений с новыми решениями парадокса часов. Любое новое решение скорее всего будет очередной ошибкой, и официозная наука тихо отринет его от себя, как она уже отказывалась от сотни предыдущих решений.
Лорду Холсбэри удалось навязать релятивистам новую форму головоломки под старым названием «парадокса часов». Идея решения парадокса трех братьев-близнецов в изложении Я.А. Смородинского выглядит следующим образом. «Предположим, — пишет он, — имеются две ракеты — одна летит от Земли вверх, а другая движется в это время к Земле. В момент вылета первой ракеты оператор сверил часы с часами космонавта. Когда космонавт встретил своего товарища, он сверил часы с ним. Второй космонавт, прибыв на Землю, обнаружит, что его часы показывают меныпе, чем часы оператора. В таком опыте участвуют трое часов и видимого парадокса не возникает»[10, c. 25].
По-видимому, Смородинский решил парадокс тем, что на веки вечные отправил второго брата-близнеца путешествовать в космос и, так как он оттуда уже болыше никогда не вернется, проблема его молодости сама собой отпадает. Если говорить серьезно, то ускорение здесь действительно отсутствует, подобно тому, как оно было исключено компенсационным приемом (рис. 9.1). Когда релятивисты согласились решать парадокс в такой форме, они тем самым признали существование проблемы времени в рамках только специальной теории относительности, без всякой ссылки на общую теорию относительности, что является с их стороны несомненным прогрессом.
На рис. 9.3а изображена диаграмма Холсбэри, где показано движение трех братьев-близнецов. Чертеж вычерчен с точки зрения брата А, который считает себя покоящимся. Согласно этому чертежу, брат С сообщает брату А факт замедленного течения времени брата В. В книге Мардера математически доказывается, что «братья В и С (в комбинации) постарели меньше, чем брат А» [8, с. 127]. Сразу же возразим, что каким бы убедительным не казалось это доказательство (с нашей точки зрения, это не математика, а какой-то бред), на самом деле никакого решения представлено не было.

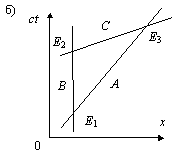
Рис. 9.3. На диаграмме (а) показаны три брата-близнеца: домосед А, летящий от Земли В и летящий к Земле С. Мардер доказал, что брат А окажется старше двух других. Однако этот автор не догадался вычертить диаграмму (б), которая продиктована принципом относительности движения, иначе бы он увидел, что все его рассуждения о старшинстве брата А нужно отнести и к двум другим братьям. Таким образом, схема трех братьев не решает парадокса часов, а только усугубляет его, что вытекает из следующего рисунка.
На рис. 9.3б вычерчена диаграмма тех же самых братьев, но уже с точки зрения брата В. Для него ранее покоящийся брат А отлетит в сторону со скоростью v. Через некоторое время мимо брата В пронесется с удвоенной скоростью брат С по направлению, куда улетел и брат А. Согласно последней диаграмме, брат С сообщит брату А факт убыстренного течения времени брата В. Если теперь провести то же самое доказательство, то окажется, что братья А и С постарели меньше, чем брат В. Далее можно вычертить такую же диаграмму относительно брата С, и тогда уже он постареет больше двух других братьев. В этом как раз и состоит трагедия релятивистов: любые математические рассуждения, проведенные в отношении одного из братьев, можно распространить на два других брата. Этого не может понять ни Мардер, ни Смородинский, ни все остальные релятивисты, лишенные пространственного воображения и мечтающие только о решении парадокса часов за счет манипуляции математическими символами. Мардер вычертил одну-единственную диаграмму рис. 9.3а, доказал, что брат А старше других, и на этом успокоился. Приведем текст его доказательства, взятый из указанной книги.
«Предположим, — пишет он, — что A, B и C покоятся в начале координат, ориентированных параллельно друг другу соответствующими осями инерциальных систем, которые мы обозначим соответственно через S, S' и S". Пусть общее положительное направление осей 0x, 0x' и 0x" совпадают с направлением движения B относительно C. Если событие первой встречи (B с A) E1 произошло в нулевой момент времени в системах S и S', то координаты любого события на совпадающих осях этих двух систем связаны... уравнениями
,
,
, c = 1. (4.1)
Допустим, что C пролетает мимо B в момент t = T. Тогда этому событию E2 соответствуют в системе S координаты x = VT, t = T, на основании же (4.1) для него в системе S' будет иметь место
x' = 0, t' = β(T – V2T) = T/β.
Событие E2 по часам брата C характеризуется также временем T/β.
Преобразования Лоренца от системы S к системе S" по форме отличается от (4.1). Во-первых, V следует в нем заменить на — V; во-вторых, уравнения (4.1) соответствуют случаю, когда начала координат обеих рассматриваемых систем совпадали в момент времени 0 по часам каждой из этих систем, чего уже не будет для S" и S. Вместо этого заметим, что событие E2 обладает в системе отсчета S координатами (VT, T), а в системе S" — (0, T/β). Это приводит к сдвигу начала отсчета пространственных и временных координат в обеих системах, который и следует учесть в искомых уравнениях:
x" = β[x – VT + V(t – T)], (4.2)
t" – T/β = β[t – T + V(x – VT)].
Встреча братьев C и A (событие E3) происходит в точке x = 0 в момент t = 2T для системы отсчета S. Согласно второму из уравнений (4.2), момент этого события в системе S" (т.е. показание часов C в момент встречи) таков: t" = T/β + β(1 – V2)T = 2T
. Это показывает, что полное время, измеренное часами B и C, в совокупности между событиями E1 и E3 меньше того, которое измерено часами A между этими событиями, и соответствующий множитель равен
. Если говорить о старении, то между этими двумя событиями братья B и C (в комбинации) постарели меньше, чем брат A» [8, с. 125 – 127].
Это нудное доказательство, конечно, ничего общего не имеет ни с физикой, ни с математикой. Автор пишет какие-то слова, между ними время от времени ставит буквы t, x, V, называя их «время», «пространство», «скорость», однако никакого отношения к реальной ситуации или хотя бы к рис. 9.3а его слова и буквы не имеют. Мне кажется, что рационально мыслящий преподаватель курса «Естествознание» на своих практических занятиях может выдавать студентам задание следующего содержания: «Найти десять отличительных признаков спекулятивного рассуждения релятивиста с верными рассуждениями конструктивиста на тему решения парадокса часов».
* * *
Если вы хотите знать, чем отличается схоластика Средневековья от схоластики Новейшего времени, текст Мардера прекрасно демонстрирует это. Старая схоластика держалась на особом сорте логики, которая у всех нормальных людей вызывала тошноту. Новая схоластика релятивистов держится на особом сорте геометрии, рвотное действие которой намного сильнее рвотного действия схоластической логики. Без всякого циркуля и линейки, с помощью какого-то эскиза, состоящего всего-то из трех пересекающихся прямых, релятивисты доказывают быстрое и медленное старение людей. Я думаю, что любой схоласт Средневековья умер бы от зависти, когда б прочел рассуждения Мардера, великие же теоретики-конструктивисты — Архимед, Коперник, Максвелл — перевернулись бы в гробу, когда б узнали, что стало с их родным детищем.
И, тем не менее, хочется с удовлетворением отметить, что доказательство Мардера имеет одно важное достоинство перед остальными решениями парадокса часов — оно короткое. Если читатель захочет испытать на себе, как на мухе дрозофиле, действие полной дозы нового схоластического препарата, он должен взять из библиотеки книгу академика В.А. Фока «Теория пространства, времени и тяготения» и открыть ее в районе 58 — 62 страницы, где излагается удивительно неправильное и путаное решение парадокса часов.
В специальной теории относительности обыкновенно рассматриваются очень простые ситуации, в которых участвуют два элемента, находящиеся в движущейся и покоящейся системах координат. При этом возникает масса проблем. Можно ожидать, что с увеличением количества элементов, число таких проблем резко возрастет. Сейчас на примере данных нам трех элементов — трех часов — мы построим принципиально иное, чем в парадоксе близнецов, противоречие.
На рис. 9.4 показаны векторы скорости движения трех братьев A, B и C относительно друг друга. Пусть брат B относительно брата A летит со скоростью vy, а относительно брата C со скорость vx. Предположим также, что (1) брат A состарится относительно брата B на TAB лет и (2) брат B состарится относительно брата C на TBC лет. Тогда (3) брат A относительно брата C должен будет состариться на TABC лет. Но если на время забыть о существовании брата B и старение брата A рассчитать непосредственно относительно брата C, то результат окажется иным. Это произойдет потому, их относительная скорость равна уже v, т.е. векторной разности скоростей vx и vy. (4) Брат A состарится относительно брата C на величину TAC лет. Утверждения (3) и (4) противоречат друг другу.
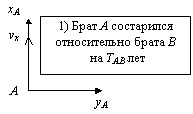

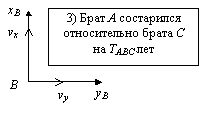

Рис. 9.4. Парадокс трех братьев-близнецов Есть три брата — A, B и C, —имеющие различную относительную скорость. Если вести сравнение по скорости старения между любыми двумя братьями, игнорируя третьего, то получится одна разность в возрасте, например TAC. Если сравнение производить с учетом третьего брата, то расхождение в возрасте будет иным — TABC.
В самом деле, пусть взаимное отставание часов выразятся формулами:

Подстановка второго выражения в первое позволит рассчитать время TABC. Однако подсчет по формуле замедления времени вида
где скорость v находится по релятивистской формуле сложения скоростей vx и vy, даст иной результат, который можно обозначить как TAC. Существование неравенства TABC ≠ TAC как раз и образует парадокс трех братьев-близнецов, который, как и парадокс двух братьев-близнецов, не имеет удовлетворительного решения.
* * *
С тем чтобы как-то решить парадокс часов, огромная масса релятивистов пошла по пути дальнейшей релятивизации времени. Раньше, в эпоху, когда жил Эйнштейн, негласно предполагается, что все часы движущейся системы K' идут единообразно, т.е. двое часов, находящихся в точках x'1 и x'2, показывают одно и то же время t', хотя и не совпадающее со временем t покоящейся системы K. Но позже преобразования Лоренца стали истолковываться так, что в точках x'1 и x'2 время идет по-разному, т.е. в этих точках часы показывают время t'1 и t'2, соответственно.
Действительно, говорят сторонники такой интерпретации, согласно преобразованию для времени:
,
при t = 0 в точках, отстоящих друг от друга на расстоянии Δx, будем иметь различный ход времени:
,
,
,
.
После этой цепочки волшебных равенств один из авторов прямо так и написал: «Чем дальше от начала координат находятся часы, тем больше они отстают» [9, c. 45].
Против такой трактовки времени возникают по крайней мере три возражения.
Во-первых, присвоение движущемуся объекту координатной оси есть дело свободного выбора субъекта теории, поэтому не понятно, какие часы должны отставать больше — те, что находятся, условно говоря, в «начале» или в «конце» рассматриваемого стержня, ведь нулевую отметку мы можем поставить где угодно.
Во-вторых, факт «отставания» часов здесь определяется отрицательным числителем, а не релятивистским квадратным корнем, как это было принято Эйнштейном и его последователями. Здесь же стоит нам изменить направление вектора скорости, т. е. заставить координатную систему К' двигаться в противоположном направлении, и мы уже будем иметь ряд из «спешащих» часов:
,
,
,
.
В-третьих, если допущена такая релятивизация времени, то должна существовать симметричная ей релятивизация пространства, т. е. при х = 0 в моменты времени, отстоящие друг от друга на период Δt, будем иметь различные эталоны длины:
,
,
,
.
Однако про релятивизацию пространственной оси, т. е. когда каждая секунда покоящейся системы отсчета К порождает в движущейся системе К' свой эталонный метр, мы от релятивистов почему-то ничего не слышали. Один абсурд порождает другой.
Как бы мы ни критиковали изложенную здесь гиперотносительность, она получила все права на существование в рамках специальной теории относительности. Главное, с помощью движущейся пространственной оси, в каждой точке которой находятся часы с различной длительностью секунды, релятивистам наконец-таки удалось убедить себя и весь ученый мир в том, что Эйнштейн в цитируемой выше работе 1905 г. не говорил глупостей.
Чтобы чего-нибудь не напутать, приведем полную выдержку из книги Гольденблата, где дано «блестящее решение» пресловутого парадокса.
«Пусть в некоторый момент времени t1 , — пишет автор, — часы A системы S (рис. 9.5) находятся против движущихся часов A' системы S'. Допустим, далее, что часы A и A' показывают одно и то же время. Часы A' движутся относительно системы S, поэтому спустя некоторое время Δt в системе S будем сравнивать их показания уже не с часами A, а с часами B, по отношению к которым они окажутся отстающими. Рассматривая то же явление с точки зрения системы S, мы видим, что для суждения об отставания часов A мы должны сравнивать их показания с часами C'. Таким образом, когда мы говорим, что часы системы S' отстают от часов системы S, мы сравниваем показания часов A' с показаниями часов B. Когда же говорим об отставании часов системы S по отношению к часам системы S', мы сравниваем показания часов A с часами C'. Таким образом, здесь каждый раз сравниваются показания различных часов, и никакого противоречия в приведенном выше утверждении нет» [10, с. 13 – 14] .
Рис. 9.5. Решение парадокса часов по Гольденблату . После смерти Эйнштейна релятивисты стали придерживаться той позиции, что в каждой точке пространства движущейся системы отсчета время идет по-разному. Поэтому при рассмотрении парадокса часов окончательно сравниваются не движущиеся часы А' с покоящимися часами А (а), а движущиеся часы A' с покоящимися часами B и покоящиеся часы A с движущимися часами C' (б). Так, невозможная ситуация одновременного выполнения условий: A' < A и A' > A (а), заменяется на возможную ситуацию: A' < B и C' > A (б).
* * *
Смотрите, читатель, какую эволюцию претерпели "решения" парадокса часов. В 1911 году релятивист Ланжевен обнаруженное в самом начале возникновения теории относительности противоречие с часами облек в забавный аттракцион с братьями-близнецами [18, c. 112]. С тех пор весь мир ученых-релятивистов только и занят решением его головоломки. Сегодня парадокс часов принял самые причудливые формы, которые, наверное, очень рассмешат наших потомков. Так, например, «Журнал экспериментальной и теоретической физики» — самый солидный журнал в нашей стране — опубликовал статью И.Д. Новикова (наш читатель с ним уже знаком) под названием «Анализ работы машины времени». Статья начинается с напоминания: «Для того чтобы попасть в будущее время какой-либо инерциальной системы отсчета, надо двигаться относительно нее с большой скоростью. Космонавт, улетающий с Земли на ракете, после возвращения оказывается в будущем Земли (так называемый парадокс близнецов)» [19, с. 769].
Какой-нибудь наивный читатель тут же предположил, что ракета космонавта это и есть машина времени. Если он так подумал, значит, он сильно отстал от достижений современной физики. Много воды утекло со времен Ланжевена и, хотя ракеты еще не вышли из моды, машину времени современные физики сконструировали на черных дырах. Пусть, предположил автор, две черных дыры A и B, соединенные между собой пуповиной, поступательно движутся в бескрайних просторах Вселенной. Пусть далее дыра В совершит судорожное колебание туда-сюда относительно дыры А. Теперь машина времени готова к эксплуатации.
«По окончании движения, — пишет ученый, — конструкция является машиной времени. Наблюдатель, войдя в В, пройдя сквозь горловину и выйдя из отверстия А, оказывается в прошлом (переход в обратном направлении переносит в будущее)» [19, с. 770]. Затем автор решил модернизировать конструкцию, заставив одну дыру кружиться на пуповине возле другой дыры.
«Пусть отверстие А все время покоится, — предположил Новиков, — а В движется вокруг него по окружности радиуса R, начиная с момента T = 0, с постоянной скоростью v = ΩR, где Ω — угловая частота движения. В инерциальной системе отсчета, связанной с A, часы B идут медленнее, чем A, из-за лоренцева сокращения времени:
» [19, с. 774].
Извини, дорогой читатель, дальше цитировать и комментировать этого ученого не могу, так как горькие слезы разочарования застлали мой взор. Только подумаешь, во что вылились сегодня релятивистские теории, и тут же начинаешь безудержно плакать. Физики больше нет, наука умерла с приходом Эйнштейна. Новиков достиг таких головокружительных высот мифотворчества, что всякий разбор его сочинений становится кощунственным. Его красочные басни, если и нуждаются в критике, то не со стороны физиков и математиков, а со стороны литераторов.
1. Угаров В.А. Специальная теория относительности — М.: Наука, 1977.
2. Дж. Льюис, Р. Толмэн. Принцип относительности и неньютоновская механика. В кн.: Новые идеи в физике. Сборник № 3, 1912.
3. Бом Д. Специальная теория относительности. – М.: Мир, 1967.
4. Эйнштейн А. К электродинамике движущихся тел. – СНТ. Т.1. – М.: Наука, 1965.
5. Полани М. Личностное знание. – М.: Прогресс, 1985.
6. Из письма к Соловину от 28 марта 1949 г.
7. Эйнштейн А. Ответ читателям «Ежемесячника популярной науки». – СНТ. Т. 2.
8. Мардер Л. Парадокс часов. – М.: Мир, 1974.
9. Купер Ф. Физика для всех. Т.2. – М.: Мир, 1974.
10. Гольденблат И.И. "Парадоксы времени" в релятивистской механике. – М.: Наука, 1972.
11. Эйнштейн А. Диалог по поводу возражений против теории относительности. СНТ.Т.1.
12. Эйнштейн А. Принципе относительности ... СНТ. Т. 1.
13. Эйнштейн А. О принципе относительности и его следствиях. СНТ. Т. 1.
14. Паули В. Теория относительности. – М., Л.: ОГИЗ – Гостехиздат, 1947.
15. Борн М. Размышления и воспоминания физика. – М.: Наука, 1977.
16. Скобельцын Д.В. Парадокс близнецов в теории относительности. – М.: Наука, 1966.
17. Терлецкий Я.П. Парадоксы теории относительности. – М.: Наука, 1966.
18. Ланжевен П. Избранные произведения. – М.: ИЛ, 1949.
19. Новиков И.Д. Анализ работы машины времени. – ЖЭТФ, т. 95, вып. 3.


|