Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.5. Пространственные группы и двойственность

Группа проективных преобразований и ее подгруппы

Мы не собираемся давать сколько-нибудь полный обзор по существующим пространственным группам преобразований, однако еще об одном пространственном преобразовании, которое называется проективным, есть смысл упомянуть, так как оно лежит в основе так называемой проективной геометрии. Она тоже подчиняется принципу двойственности, поскольку является обыкновенным расширением группы только что рассмотренного преобразования. Далее под x и x' можно по-прежнему понимать комплексные числа, однако в дальнейшем нам нужно подчеркнуть некоторые важные групповые свойства преобразований, не зависимо от того, к числам какого характера они относятся. Поэтому проще, если под x и x' мы будем понимать вещественные числа.

Итак, проективным называется преобразование вида:

, = ad – bc ≠ 0.

Совокупность этих преобразований образует пространственную группу. Геометрия, основанная на проективных преобразованиях, называется проективной. Точке x = – d/c в штрихованном пространстве ставится в соответствие бесконечно удаленная точка x' = ∞, которой нет, например, в евклидовой геометрии, почему в ней и не действует принцип двойственности.

Исходя из двух преобразований: x → x' и x' → x", найдем результирующее x → x":

,     ,     = 

= = .

Из этого перемножения видно, что коэффициенты результирующего преобразования находятся по закону перемножения матриц:

= = .

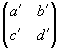
Если тождественное преобразование определить как

, то обратное к будет ,

что проверяется подстановкой. Инвариантом проективной группы является двойное, или ангармоническое, отношение четырех точек:

.

Перестановка точек x_i приводит еще к пяти другим выражениям.

Если проективные преобразования образуют группу, то каковы будут ее подгруппы? — Ими являются преобразования, которые получают обнулением одного, двух или трех коэффициентов. Вместе с тождественным имеем девять подгрупп:

x' = x,     x' = ax,     x' = ax + b,     ,     ,

,     ,     ,     ,     .

Некоторые из перечисленных подгрупп имеют в математике устоявшиеся названия: x' = ax — группа растяжения, x' = b/cx — группа сжатия, x' = ax + b — группа аффинных преобразований прямой, которая определяет аффинную геометрию; если a = 1, то получим группу скольжения — x' = x + b. В физике группа поступательного движения x' = x + vt получила название преобразований Галилея, а группу преобразований Кэли – Клейна, впервые рассмотренную Кэли в его шестом математическом мемуаре 1859 г., физики позднее назвали преобразованиями Лоренца.

Проективная группа имеет две подгруппы в зависимости от знака определителя, который можно нормировать на единицу:

= ad – bc = ±1.

Какие бы числовые значения ни принимали четыре коэффициента, элементы подгруппы с положительным определителем при перемножении между собой никогда не дадут элемент с отрицательным определителем, и наоборот.

Основным свойством групп вообще и пространственных в частности является их замкнутость. Всякий математик сильно удивится, если кто-то, перемножая два элемента из группы тетраэдра, заявит, что он получил элемент из группы кватерниона. Точно так же невозможно путем изменения какого-либо параметра (путем его постепенного уменьшения до нуля или его увеличения до бесконечности) перейти из одной группы преобразований в другую.

Так, группа аффинных преобразований вида x' = (ax + b)/d может дать элементы, принадлежащие только этой же группе. Проверим справедливость данного утверждения на числах. Пусть даны два преобразования x → x' и x' → x", найдем результирующее x → x":

,     ,     ;

результат имеет вид исходных преобразований. Поскольку в аффинную группу входит в качестве подгруппы преобразование растяжения (x' = ax), то за счет предельного перехода параметров (b → 0, d → 0) можно получить из элементов аффинной группы элемент группы растяжения.