Эфир (Часть 4) Учения Декарта и Ньютона
О.Е. Акимов

Сначала посмотрите этот двухминутный детский ролик ("Spaceship Earth", written and directed by Nicolas Gessner, produced by Fantome Animation), а потом вернемся к нашим проблемам.
 Закадровый текст: "Это – Земля, наш космический корабль. Мы продолжаем путешествие вокруг Солнца. Что толкает Землю вперед? – Импульс, который она получила в момент образования. Закон притяжение был открыт Исааком Ньютоном в XVII веке. Говорят, что ему на голову упало яблоко, и он задумался: почему? Потому что огромная масса Земли притягивает крошечное яблоко. Это – сила тяжести. Почему же Луна не падает на Землю, а Земля на Солнце? Потому что притяжение Солнца компенсируется инерцией Земли, которая бы унесла нас в бесконечность по прямой траектории. Земля постоянно старается вырваться, но ее удерживают силы притяжения Солнца, и в то же время мы всегда падаем на Солнце, но нас спасает сила инерции. Орбита Земли – кривая, которая уравновешивает эти две силы. Масса Солнца удерживает Землю на орбите; масса Земли удерживает около себя Луну. Орбита Луны – это кривая, уравновешивающая силу инерции, направленную вдаль от Земли, и силу притяжения Земли, которая сама по себе заставила бы спутник упасть на планету".
Закадровый текст: "Это – Земля, наш космический корабль. Мы продолжаем путешествие вокруг Солнца. Что толкает Землю вперед? – Импульс, который она получила в момент образования. Закон притяжение был открыт Исааком Ньютоном в XVII веке. Говорят, что ему на голову упало яблоко, и он задумался: почему? Потому что огромная масса Земли притягивает крошечное яблоко. Это – сила тяжести. Почему же Луна не падает на Землю, а Земля на Солнце? Потому что притяжение Солнца компенсируется инерцией Земли, которая бы унесла нас в бесконечность по прямой траектории. Земля постоянно старается вырваться, но ее удерживают силы притяжения Солнца, и в то же время мы всегда падаем на Солнце, но нас спасает сила инерции. Орбита Земли – кривая, которая уравновешивает эти две силы. Масса Солнца удерживает Землю на орбите; масса Земли удерживает около себя Луну. Орбита Луны – это кривая, уравновешивающая силу инерции, направленную вдаль от Земли, и силу притяжения Земли, которая сама по себе заставила бы спутник упасть на планету".
Почему же Луна не падает на Землю, а Земля на Солнце?Сегодня многие знает, что история с падением яблока придумана Ньютоном, когда известный английский археолог, исследователь Стоунхенджа Вильям Стьюкли (William Stukeley, 1687 – 1765), поинтересовался, что послужило причиной открытия всемирного закона тяготения. Ньютон рассказал ему, как однажды он сидел под яблоней; неожиданно с ветки упало яблоко. "Почему яблоки всегда падают перпендикулярно вниз, к земле?" – подумал ученый. Эта мысль, якобы, и послужила толчком к дальнейшим размышлениям. Легенда с яблоком стала широко известна благодаря Вольтеру, французскому просветителю, который восхищался работами прославленного англичанина.

Английский археолог, исследователь Стоунхенджа
Вильям Стьюкли (William Stukeley, 1687 – 1765),
которому Ньютон поведал легенду о яблоке.

Вольтер, французский просветитель, который восхищался работами
Исаака Ньютона, ничего не понимая ни в математике, ни в физике.Но сегодня из черновых записей Ньютона мы хорошо знаем, что ничего подобного не было. К всемирному закону тяготения Ньютон пришел не самостоятельно. А самое главное, что нас сейчас интересует, Ньютон даже после написания своих "Начал" до конца не понимал, почему Луна вращается вокруг Земли, а Земля – вокруг Солнца. В только что просмотренном нами фильме рассказывается, что круговое движение малого тела вокруг большего можно разложить на две составляющие. Одна из них направлена к центру тела с большей массы. Она образует равноускоренное движение по причине всемирного закона тяготения. Вторая составляющая направлена по касательной к орбите малого тела. Она вызвана инерционным движением малого тела. Их совместное движение дает круговую или эллиптическую орбиту, если инерционная скорость не превышает так называемую вторую космическую скорость, т.е. не больше 11 км/сек.

Титул "Математических начал" Ньютона.
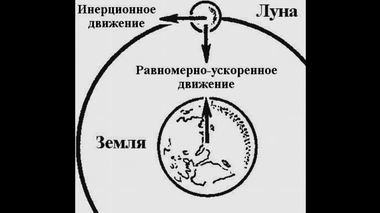
Круговое движение малого тела вокруг большего
можно разложить на две составляющие.В предыдущей части, рассказывающей о становлении физической науки, мы указали на несколько мест в объемистом томе третьего вполне завершенного издания "Математических начал", где Ньютон выражается как-то уж очень странно, прежде всего, относительно первого закона механики, касающегося инерции. В формулировке этого закона совмещены два противоположных понятия – пассивности и активности инерции. Это вызвало определенные трудности при переводе латинского текста "Начал" на другие языки, в частности, русский. О трудностях перевода книги наш прославленный академик Алексей Николаевич Крылов говорил в отдельных примечаниях.

Исаак Ньютон. Многие считают его гениальным физиком.

Алексей Николаевич Крылов – переводчик
"Математических начал" на русский язык.Активная характеристика инерции, как некой врожденной силе, проявляется в упорстве тела сохранять существующее состояние. Массивное тело нелегко заставить двигаться, если до этого оно покоилось. Тело активно сопротивляется приложенной к нему внешней силе. И, наоборот, тело может легко перемещаться сколь угодно долго, если ему ничто не помешает. Кажется, что тело вбирает приложенную к нему внешнюю силу и, каким-то образом, сохраняет ее внутри себя. Опыт всегда показывал, что сохранение движения тела не длится вечно: рано или поздно оно останавливается. Декарт интуитивно, т.е. не на опыте, а единственно своим абстрактным разумом, догадался, что однажды выведенное из состояния покоя тело никогда больше не остановится, если ему ничто не мешает, например, сопротивление воздуха или какое-то другое тело.

Некоторые дефиниции Ньютона содержат подводные камни

Солнечная система после мгновенного исчезновения Солнца.В 1980 году Ричард Сэмюэль Вестфолл (Richard Samuel Westfall) опубликовал книгу о Ньютоне под названием Never at Rest (Без отдыха или Ни минуты покоя). Название говорит нам, что Ньютон был настоящим трудоголиком. Огромную книгу в 900 страниц Вестфолл переиздал в сокращенном и более популярном виде в 1993 году под названием Жизнь Ньютона (The Life of Isaac Newton). К ней мы сейчас и обратимся. В третьей главе, которая называется Anni mirabiles – Чудесный год, т.е. год 1665, когда, по словам Ньютона, им был открыт всемирный закон тяготения, Ричард Вестфолл прослеживает эволюцию взглядов этого английского ученого.
Титул главного труда Ричарда Вестфолла Без отдыха

Anni mirabiles – Чудесный год, т.е. год 1665, когда,
по словам Ньютона, им был открыт всемирный закон тяготения.Автор напоминает обстоятельства отъезда студента Ньютона в своё родное имение Вулсторп. Причиной послужила эпидемия чумы, вспыхнувшая в Англии, в том числе, в Кембридже. Исаак уехал из университетского городка в августе 1665 года, а вернулся туда в апреле 1667 года. По его же воспоминаниям, годы эпидемии были для него очень плодотворными. Он пишет:


Вулсторп и Кембридж«В начале 1665 года я нашел метод приближенного вычисления рядов и правило превращения любой степени двучлена в такой же ряд [это бином Ньютона]. В мае того же года я нашел метод касательных Грегори и Слузия, в ноябре получил прямой метод флюксий [т.е. дифференциальное исчисление]; в январе следующего года я получил теорию цветов, а в мае приступил к обратному методу флюксий [т.е. интегральное исчисление].
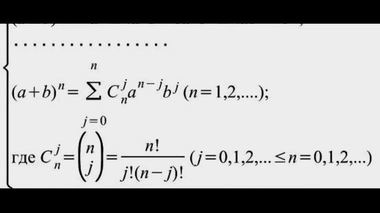
Формула бинома Ньютона.

Титул работы Ньютона "Метод флюксий и бесконечные ряды".В том же году [т.е. 1666-м] я начал размышлять о действии тяжести, простирающейся до орбиты Луны, и, найдя, как вычислить силу, с которой тело, обращающееся внутри сферы, давит на поверхность этой сферы, я вывел из [третьего] закона Кеплера, по которому периоды обращения планет находятся в полуторной пропорции [3/2] с расстояниями их от центров орбит, что сила, удерживающая планеты в их орбитах, обратно пропорциональна квадратам их расстояний от центров обращений.

Кеплер
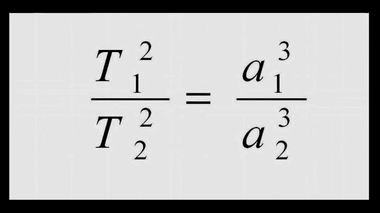
Третий закон Кеплера.При этом я сравнил величину силы, потребной для удержания Луны на ее орбите, с силой тяжести на поверхности Земли и нашел между ними приблизительное равенство. Всё это имело место во время чумы 1665 – 1666 годах; в это время я переживал лучшую пору своей юности и больше интересовался математикой и философией, чем когда бы то ни было впоследствии».

Великая чума 1665 – 1666 гг.В третьей части фильма об эфире говорилось, что "история науки еще не знала такого плагиатора, каким был Ньютон". В этой связи мы привели письмо Ньютона от 18 мая 1669 года, адресованного его другу Френсису Астону. Кстати, Астон впоследствии стал секретарем Лондонского Королевского общества. В этом его качестве Ньютон в конце февраля 1685 года обратился к нему, чтобы официально зафиксировать начало работы над сочинением "О движении", которое, в итоге, превратилось в "Математические начала натуральной философии".

Письмо Ньютона Френсису Астону от 18 мая 1669 года

Заседание Лондонского Королевского общества.Какую именно рукопись Ньютона научный секретарь Френсис Астон внес в регистрационную книгу Королевского общества в качестве доказательства приоритета Ньютона, никто толком не знает. Сопроводительное письмо, приложенное к наброскам будущего сочинений, переданное Ньютоном Астону, было оглашено на очередном заседании Общества. В нем, в частности, говорилось: «Я предназначал их [т.е. наброски сочинения] для Вас уже давно, но проверка некоторых вещей заняла больше времени, чем ожидалось, и в основном оказалась напрасным трудом. А сейчас я отправляюсь на месяц-полтора в Линкольншир. После чего, – заверил Ньютон секретаря, – я намереваюсь окончить всё по возможности быстро».


Современная фотография подъезда № 7
здания Лондонского Королевского общества.Слова "оказалась напрасным трудом" – это очень важная оговорка. Ньютон признавал, что был на ложном пути, почему, собственно, и отложил работу над сочинением. Если бы дела шли хорошо, он не стал бы прерывать работу и никуда бы не уезжал. Но вернемся к фрагменту воспоминания Ньютона о "чудесном периоде".

Здесь жил Ньютон.Этот фрагмент цитируется и комментируется многими историками науки, но никто, кроме Ричарда Вестфолла, не удосужился прокомментировать загадочную фразу и, найдя, как вычислить силу, с которой тело, обращающееся внутри сферы, давит на поверхность этой сферы. Ясно, что под телом в данном случае имеется в виду Луна. Но как можно представить себе обращение Луны внутри сферы? Какой сферы, собственно? Очевидно, подразумевается сфера, на поверхности которой лежит орбита Луны. Однако, всё равно не ясно, как Луна может давить на поверхность сферы, т.е. на орбиту Луны, с внешней стороны траектории. Обратите внимание, здесь ничего не говорится об инерционном движении Луны, т.е. о тангенциальной составляющей движения малого тела.

Тангенциальная и радиальная составляющие движения малого тела.В третьей главе книги Вестфолла Anni mirabiles мы находим рисунок 2, который дает ключ к пониманию "Математических начал натуральной философии". Прошло 34 года с момента публикации первой полной версии книги Вестфолла Never at Rest, так что сегодня появилось множество критических книг и аналитических статей, в которых публикуется этот или аналогичные чертежи и дается детальный анализ того, что, собственно, сделал Ньютон в области фундаментальной динамической задачи, которая во второй половине XVII века вышла на первый план физических наук. Ее частично решил Кеплер в начале XVII века, когда сформулировал три закона, названных его именем.
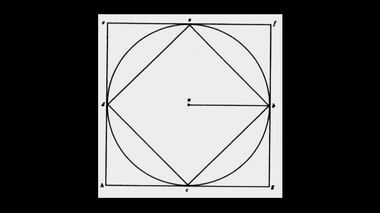
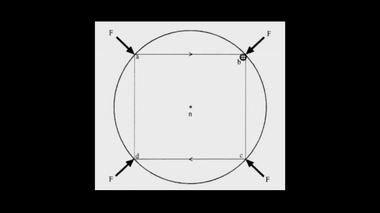
Ключи к пониманию "Математических
начал натуральной философии".Ход мыслей Ньютона, связанный с приведенными выше чертежами, прекрасно иллюстрируется анимационным видео-роликом, созданным при помощи компьютера. Сейчас мы видим траекторию тела, в принципе, это может быть Луна или любое другое небесное тело, движущегося по периметру квадрата. В вершинах квадрата телу сообщается импульс, обозначенный здесь белой стрелкой. Под воздействием этого импульса траектория тела внутри круга меняется. Увеличим число сторон, и квадрат превращается в пятиугольник. Внешние импульсы по-прежнему воздействуют на тело, меняя его траекторию. Еще увеличим число сторон: сейчас пятиугольник превратился в шестиугольник. Этот многоугольник имеет уже 10 сторон. Еще увеличим число сторон, потом еще и еще. Таким образом, мы видим, как многоугольник превратился в окружность, т.е. в круговую орбиту Луны.
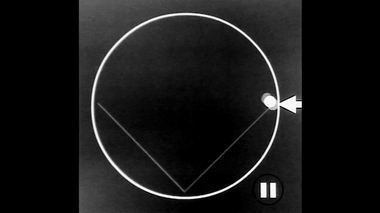

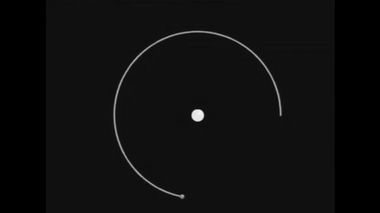
Движение тела по сторонам квадрата, многоугольника и по окружности.С чем мы имеем дело? Причем здесь Луна? А где Земля в таком случае, т.е. центральное гравитирующее тело, которое, собственно, и должно удерживать Луну на круговой орбите? Наконец, откуда взялись периодические импульсы, действующие на тело с внешней стороны лунной орбиты? Пока мы видим некое приближение (говорят, аппроксимацию) круговой орбиты с помощью многоугольника, число сторон которого увеличивают до бесконечности. Между тем, именно эта идея пришла в голову Ньютона в чумной 1666 год, когда студент Тринити-колледжа уединился в своем родном имении Вулсторп и принялся тщательно изучать аналитическую геометрию и философию Декарта.
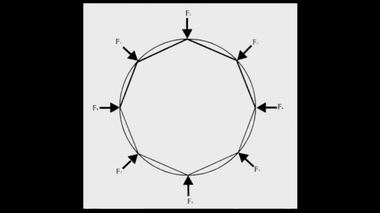
Аппроксимация окружности многоугольником.Мы помним, согласно Декарту, Вселенная наполнена космическими вихрями эфира шарообразной формы. Вращение планет и их спутников сформировалось под воздействием этих вихрей. В третьей части фильма, мы уже говорили, что Вселенная Декарта непрерывно эволюционирует. Ячеечная структура вихрей постепенно меняется.
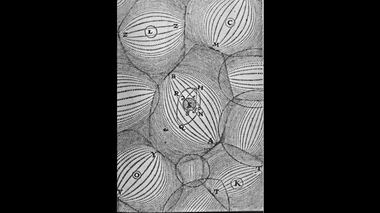

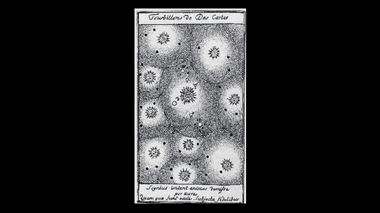
Космические вихри Декарта.Сейчас мы подойдем к философии Декарта более основательно. С этой целью обратимся к двум его работам, а именно: " Мир, или Трактат о свете" (1634 года издания) и "Принципы философии", в русском переводе "Первоначала философии" или просто "Начала" или "Принципы", вышедшие в 1644 году. Принципы разделены на четыре части. Первая: Принципы человеческого познания; вторая: Принципы существование физических вещей. Если в первых двух частях рассказывается о сущностных вещах, то две последующие части касаются феноменологии космоса – это третья часть, и отдельно Земли – это четвертая часть.
Первым пунктом первой части декартовских "Начал" стоит такой: Познающему человеку нужно хоть раз в жизни усомниться во всех вещах – насколько они возможны. Мы должны также считать все сомнительное – ложным; это второй принцип философии Декарта. Ведь мы располагаем свободой избежать заблуждения – шестое положение. Седьмой пункт: Мы верим, что, пока мы сомневаемся, мы существуем, и эта уверенность является на самом деле первым пунктом философии.
Таким образом, Декарт свое скептическое негативное отношение к миру выразил сугубо позитивной сентенцией: Я мыслю, следовательно, я существую. Это – первичное и достовернейшее положение, которое приходит в голову любому познающему субъекту. Из этого проистекает понимание принципиального различия между душой и телом, или между вещью мыслящей и телесной (такова идея 8 пункта "Принципов философии" Декарта).
То, что является простым и само собой разумеющимся, строгие дефиниции могут только затемнить (10 пункт философии Декарта). Рассуждать о бесконечном не допустимо, следует просто считать вещи безграничными, если вы не видите границ (пункт 26 философии Декарта). Но и конечные вещи не подобает изучать философу. Ему нужно искать причины и сущность вещей, а не мимолетные проявления (пункт 28). Мы плохо судим, когда выражаем согласие с тем, что воспринято не ясно, а случается это потому, что мы считаем, будто ранее достаточно вникли в проблему (пункт 44). Чтобы искоренить в себе предрассудки молодости, надо проанализировать элементарные понятия (пункт 47).
Каждой субстанции присущ один главный атрибут, как мышление – уму, а протяженность – телу (пункт 53). Одни атрибуты присущи самим вещам, другие – нашему мышлению (пункт 57). Мы часто ошибаемся даже в отношении ощущения боли. Таким же образом обстоит дело в отношении всего прочего, вызывающего у нас ощущения (пункт 67).
Переходим ко второй части "Начал", касающихся принципов существования физических вещей. По Декарту, мир создал Бог из материи, которая целиком заполняет данное им пространство; пустота отсутствует. "Тела переходит из одного места в другое, последовательно занимая всё пространство, находящееся между этими местами", – говорит французский философ. Чтобы лучше представить такое перемещение, он предлагает понаблюдать за рыбами, которые легко перемещаются в воде, которая не имеет никаких пустот.
Частицы материи "движутся с такой огромной скоростью и так малы, что нет других тел, способных остановить их". Эти первочастицы не имеют определенной величины, формы и расположения в пространстве. Они образуют первый элемент, который лишен каких бы то ни было свойств: тепла, холода, влажности, сухости. Он не имеет ни запаха, ни вкуса, ни цвета, ни звука, ни каких-либо других свойств реальных объектов.
Однако Декарт не хочет признавать материю в качестве абстрактного объекта, как это делают некоторые философы. "Представим нашу материю, – пишет он, – реальным телом, совершенно плотным, одинаково заполняющим всю длину, ширину и глубину того огромного пространства, на котором остановилась наша мысль". "Я рассматриваю протяженность материи и ее свойство занимать пространство не как акциденцию, а как ее истинную форму и сущность". "Кроме того, будем считать, что Бог действительно разделил ее на множество таких частей, из которых одни больше, другие меньше, одни имеют одну форму, другие – другую".
"Я рассматриваю материю со всеми присущими ей качествами, предполагая, что Бог сохраняет все сотворенное им в том же самом виде, как это было при сотворении мира. Из того, что материя сохраняется в неизменном виде, вытекает, что должны произойти некоторые изменения в ее частях. Эти изменения, как мне кажется, – пишет Декарт, – нельзя приписать непосредственно действию Бога, поэтому я приписываю их природе. Правила, по которым совершаются эти изменения, я называю законами природы".
"Первое правило (или, первый закон природы) заключается в следующем: Каждая частица материи в отдельности продолжает находиться в одном и том же состоянии до тех пор, пока столкновение с другими частицами не вынуждает ее изменить это состояние".

Декарт"В качестве второго правила (или, закона), – говорит Декарт, – я предполагаю следующее: Если одно тело сталкивается с другим, оно не может сообщить ему никакого другого движения, кроме того, которое оно потеряет во время этого столкновения, как не может и отнять у него больше, чем одновременно приобретает".
"В качестве третьего правила (или, закона) я прибавляю, что, хотя при движении тела его путь чаще всего представляется в виде кривой линии и невозможно произвести ни одного движения, которое не было бы так или иначе круговым, тем не менее, каждая из частиц тела в отдельности всегда стремится продолжать его по прямой линии".
Этими тремя правилами, сформулированными в "Трактат о свете" 1634 года, Декарт заложил фундамент современной физики, периодически воспроизводимый с теми или иными вариантами Гуком, Ньютоном и другими мыслителями Нового времени. В свете поставленных задач, более всего нас интересует третье правило (или, закон природы). При вращении камня в праще, камень постоянно имеет склонность двигаться по прямой линии, по кругу же он идет только по принуждению. Однако в природе нет иного движения, кроме кругового. Чтобы пояснить эту важную мысль, Декарт приводит пример с бочкой, полностью заполненной вином. Не станем его анализировать, поскольку пример неудачный, философ в данном случае ошибся.
В главе 5 "Трактата о свете", которая называется "О числе элементов и о качествах ", автор развивает свое учение о первоматерии. Помимо первого элемента, даруемого Богом, в мире имеется второй элемент, производимый уже Природой. Он состоит из частиц среднего размера и не столь быстрых, как частицы первого элемента. Наконец, есть частицы третьего природного элемента. Они имеют большие размеры, легко сливаются друг с другом и, как правило, препятствуют движению частиц первого и второго элемента.
Первый, второй и третий элементы можно назвать огнем, водой и землей (воздух Декарт представил как сильно разряженную жидкость), только прямого сходства с реальным огнем, водой и землей у элементов нет, так как из-за своей малости они не воспринимаются зрением. Их можно было бы ассоциировать с атомами Демокрита, но атомы предполагают пустоту, а Декарт исключил ее из своей картины мира. В реальном огне, воде и земле присутствуют все три элемента в преимущественных количествах и они обладают определенными качествами, которые мы ощущаем.
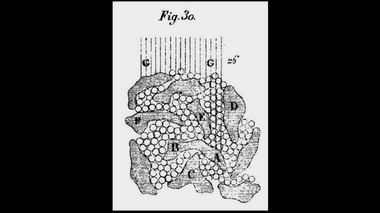
"...Хотя мы предполагаем, что сначала частицы были всевозможных видов и что у большинства из них было много углов и много сторон, подобно кускам разбитого камня, однако впоследствии, двигаясь и сталкиваясь друг с другом, они должны были постепенно обломать острые вершины своих углов и сгладить грани своих сторон. Вследствие этого частицы стали почти круглыми, подобно тому, как это происходит с песчинками и галькой, когда они катятся, увлекаемые водой реки".
"...Частицы, имевшие неправильную форму, вместо того чтобы ломаться и округляться, соединялись с другими частицами. Эти частицы сохранили форму третьего элемента и послужили материалом для образования планет и комет".
Главными объектами Вселенной является, во-первых, Солнце и неподвижные звезды, в которых преобладает первый элемент; во-вторых, небо и океан, в которых преобладает второй элемент; и, в-третьих, Земля, планеты и кометы, которые состоят преимущественно из третьего элемента. Землеподобные объекты отражают и преломляют свет, исходящий из солнцеподобных объектов. Свет образован частицами первого элемента, которые становятся видимыми благодаря наличию объекта с преобладанием частиц 2 и 3 элемента. Воздух и вода преломляют свет, частично отражая его, а Земля, планеты и кометы либо полностью поглощают свет, либо частично отражают его. "Что же касается неба, – пишет Декарт, – то, поскольку оно для нас неощутимо, есть основание считать его природу средней между природой светящихся тел, действие которых мы воспринимаем, и природой твердых и тяжелых тел, сопротивление которых мы ощущаем."

ДекартИтак, перед нами стройная, хорошо продуманная философия, которую Декарт не колеблясь принял еще в молодые годы, а позже только добавлял и развивал ее отдельные положения. Всё иначе было у Ньютона. Он никогда не имел своей собственной философской системы, вечно сомневался в эллиптично принятых им положениях, выхваченных у разных мыслителей, в том числе, Декарта. Чтобы понять, насколько ошибочно Ньютон понял французского философа, нам нужно перейти к рассмотрению третьей части декартовских "Начал", где рассматриваются движения небесных тел. Но прежде скажем несколько слов об источниках.

НьютонНа русский язык переводился "Трактат о свете" и только первая часть "Принципов философии" Декарта, которые вошли в 2х-томник известной у нас в стране книжной серии "Философское наследие". В Интернете вы легко отыщите и Трактат и Принципы на языке оригинала, т.е. латинском, а также на французском, немецком и английском языках. Содержание Трактата и третьей части Принципов во многом пересекаются. Главная идея, объединяющая Декарта и Ньютона, ясно изложена в Трактате, который можно найти, например, в библиотеке Якова Кротова, известного ведущего радиопередач на религиозные темы. Из третьей части Принципов, в которой всё очень подробно разжевывается и где много лишнего для нас, мы позаимствуем рисунки.


"Принципы философии" Декарта.Кроме того, в Интернете имеется множество сайтов, которые пересказывают точку зрения Декарта на строение Вселенной. Себе в помощь мы возьмем книгу Туфайя Хайдарзадэ – не знаю, насколько точно я произношу имя автора (Tofigh Heidarzadeh); книга называется История физических теорий комет от Аристотеля до Уиппла (A History of Physical Theories of Comets, From Aristotle to Whipple). В третьей главе От Браге до Ньютона автор знакомит нас с общим учением Декарта о строении космоса, включая его теорию комет, рассказывая о загадочных траекториях и пугающих хвостах этих небесных скитальцев.

Книга Туфайя Хайдарзадэ "История физических
теорий комет от Аристотеля до Уиппла".Появление комет в небе над Европой сыграло важную роль в формировании физической картины мира. Жаркие споры вспыхнули с появлением крупной кометы 1618 года. Тут же о кометах заговорили в светских салонах и, разумеется, в сообществе ученых. Мнения авторитетных астрономов – Галилея, Кеплера, Декарта, Ньютона, Галлея и прочих известных исследователей комет вытеснили фантастические домыслы о гибельном предзнаменовании, которые следует ожидать в ближайшем будущем.


Хвосты комет

Кометы – гибельное предзнаменование.Возникновение мира Декарт связал с творением Всевышнего, но дальнейшее его эволюционное развитие происходило естественным путем силами вихревого движения. Бог наполнил космос первичной массой, состоящей из частиц, которые были вполне однородными, хотя и неправильной формы. Каждая частица вращалась вокруг собственной оси. Затем, частицы разделились на группы. Каждая группа вращалась вокруг какого-то общего центра. Совместное движение частиц неправильной формы приводило к округлению первичной формы, острые углы откалывались, поверхность сглаживалась. Процесс напоминал образование гальки, песка и глины в бурном потоке реки.

Бог наполнил космос первичной материей.
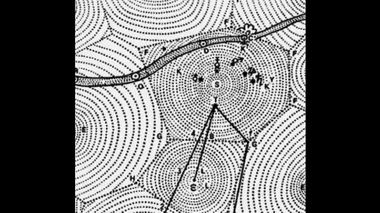
В процессе эволюции из первоматерии образовались вихри.Мелкие сколы и просто пыль, возникшая в результате трения, образовали первый элемент, обозначенный здесь как Е1. Совокупность сферических частиц, полученных путем притирки, образовали второй элемент, обозначенный как Е2. Наконец, возник еще и третий элемент Е3. Он состоял из комков неправильной формы и сравнительно больших размеров. Каждый комок представлял собой конгломерат, состоящий из мельчайших фракций Е1, более крупных сколов, которые нельзя было отнести к элементу Е1, и первичных частиц неправильной формы, которыми Бог изначально заполнил космос. В нижней части этого рисунка показан конгломерат из всех трех типов материи.
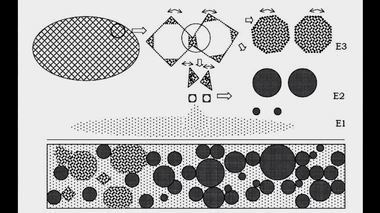
Три формы элементов Е1, Е2 и Е3.
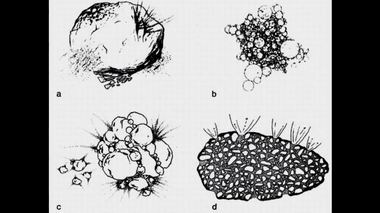
Кометы
Солнце и звезды состоят из элемента Е1.
Тело цикла образовано преимущественно из элемента Е2.
Планеты и кометы – из элемента Е3.По мнению Декарта, Солнце и звезды целиком состоят из мельчайших легко текущих частиц Е1. Планеты и кометы сделаны только из третьего элемента Е3, а весь объем вихря заполнялся более густой, но все же текучей массой, состоящей из первого элемента Е1 и преимущественно второго элемента Е2. Таким образом, вещество Солнца и звезд просто кипит, частицы Е1 совершают быстрые вращательные движения. Каждая звезда, включая Солнце, находится в центре больного сравнительно медленно вращающегося вихря, под действием которого вращаются планеты и их спутники. Кометы двигаются по слегка изогнутым траекториям между вихрями в соприкасающихся слоях, которые далеки от звезд и планет.
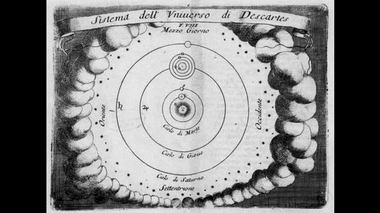
Солнечная система по Декарту.

Солнечная система по Копернику.
На данном рисунке показано строение большого вихря, состоящего преимущественно из массы Е2 частиц. Ближе к периферии вихря пунктирной линией показано разделительное кольцо (дивайдинг ринг). За ним располагаются внешние слои вихря, соприкасающиеся с внешними слоями других вихрей. Направление вращения внешних слоев не определено и зависит от мощности вращения данного вихря и соприкасающихся вихрей.
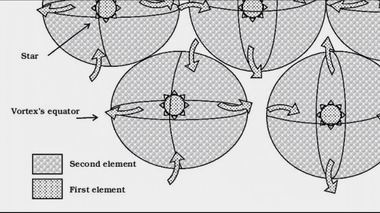
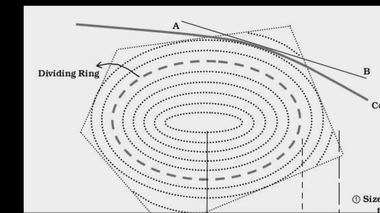
Строение вихря. Направление вращения
внешних слоев не определено.На рисунке проведена касательная АВ и участок кометной траектории . Внизу под вихрем приведены два графика. Кривая 1 показывает размеры частиц 2-го элемента. В центре вихря, где находится звезда (сама звезда не показана) размеры частиц минимальны. Ближе к разделительному кольцу размеры частиц Е2 постепенно увеличиваются. С внешней стороны разделительного кольца частицы материи Е2 уже не возрастают. Кривая 2 демонстрирует нам скорость частиц Е2. Ближе к центру она максимальна, по мере приближения к разделительному кольцу она падает до нуля, а за разделительным кольцом она снова нарастает, так как в этом слое происходит сложение скорости внешнего потока данного вихря и скорости внешнего потока соседнего вихря.
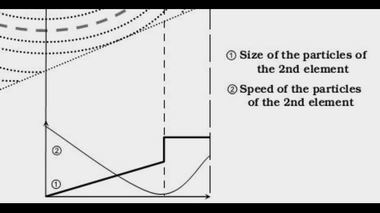

Два графика. Вихрь Солнечной системы.Итак, чем больше скорость вращения вихря – неважно какого, большого или маленького – тем больше в нем элемента Е1 (звездного вещества), Е2 – элементы среднего размера (это – тонкая материя, образующая основной объем вихря), а из элемента Е3 состоят планеты и комета – потухшие звезды.
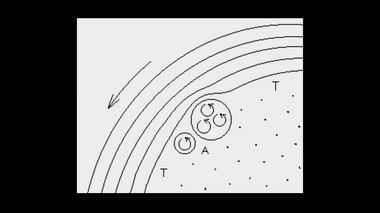
Большие (Т) и маленькие (А) вихри:
чем больше скорость вращения вихря,
тем больше в нем энергии и элемента Е1.Теперь мы готовы ответить на ранее поставленный вопрос, а именно, что означает фраза Ньютона "и, найдя, как вычислить силу, с которой тело, обращающееся внутри сферы, давит на поверхность этой сферы" и т.д. Эта фраза увязывается с рядом чертежей и анимационным видео-роликом, на которых показана окружность, внутри которой по хордам движется некое материальное тело, например, Луна. Каждая новая хорда – это сторона правильного многоугольника. В момент касания тела с окружностью, которая является орбитой тела, с внешней стороны окружности действует импульс. Этот импульс изменяет прямолинейную траекторию тела, перемещающегося по стороне многоугольника, на новую сторону.
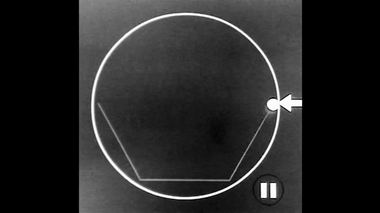
Каждая новая хорда – это сторона правильного многоугольника.Откуда взял 23-летний студент Тринити-колледжа это странное истолкование движение Луна вокруг Земли? Ньютон тщательно скрывал источник не ему пришедших идей. К счастью, источник именно этой идеи скрыть невозможно, поскольку имя Декарта было у всех на устах, а его взгляды в то время многим были известны.

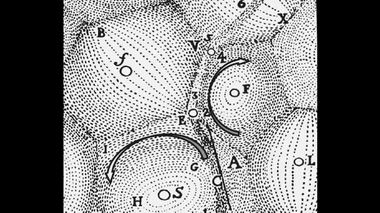
Имя Декарта было у всех на устах.В книге декартовских "Начал" имеется следующий рисунок, на котором F - центр вихря, G - центр Земли, Н - море, I - воздух. Е - Луна, которая движется по орбите ABCD. Объем АС - заполняется тонкой материей – K, которую во времена Декарта принимали за эфир. Эфир K находится над слоем воздуха (I), воздух – над морской водой (Н), а вода – над земным шаром (G). Идея этого рисунка предельно проста.
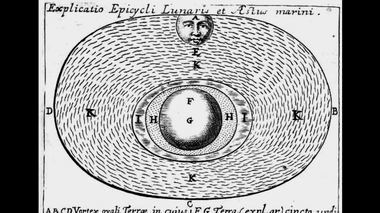
Солнечная система по Декарту: Эфир K находится над слоем воздуха (I),
воздух – над морской водой (Н), а вода – над земным шаром (G).Луна A (изображена с человеческим лицом) под действием эфирного вихря K вращается вокруг центра F, но не вокруг земного центра – G. Земля не является телом притяжения Луны. Это – аналогичный рисунок. Луна находится тоже вверху, в точке В. Она вращается по орбите ABCD. Земля покрыта водами морей; воздух находится над ними; атмосфера переходит в тонкую материю эфира. Обратите внимание: здесь, как и на предыдущем рисунке, центр вихря (он взят в кружочек и обозначен буквой М) не находится в центре Земли, который находится ниже, в районе буквы Т.
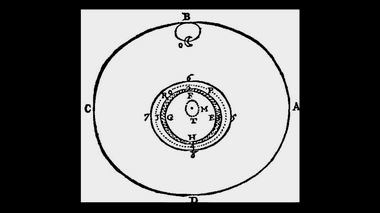
Это – аналогичный предыдущему рисунок.
Луна находится тоже вверху, в точке В.
Она вращается по орбите ABCD.
Возникает вопрос: если не сила тяготения вращает Луну вокруг Земли, то под действием чего она перемещается по внутренней стороне окружности? Декарт придумал следующий механизм. Он описал его в 11-й главе "Трактата о свете", которая называется "О тяжести". Читаем с самого начала:
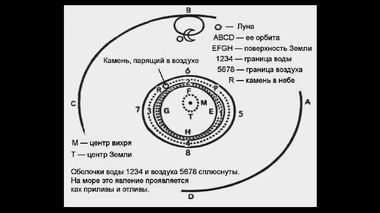
Предыдущий рисунок, но уже с расшифровкой всех обозначений."Теперь я хочу, чтобы вы рассмотрели, что представляет собой тяжесть этой Земли, т.е. сила, которая соединяет все ее частицы и заставляет их стремиться к ее центру в большей или меньшей степени, в зависимости от их величины и плотности. Сила эта состоит только в том, что частицы малого неба, окружающего Землю, вращаясь гораздо быстрее вокруг ее центра, чем частицы Земли, с большей же силой стремятся от нее удалиться и, вследствие этого, отталкивают туда последние".
То есть, землеподобные частицы, из которых состоит Луна, стремятся к Земле, а более быстрые и легкие частицы стремятся удалиться от неё.
"Представьте теперь, – пишет Декарт, – что это небо и эта Земля вращаются вместе вокруг центра Т и что, следовательно, все их частицы стремятся удалиться от этого центра. Частицы неба должны гораздо сильнее стремиться удалиться от центра, чем частицы Земли, поскольку у них больше скорость. Точно так же частицы Земли, с наибольшей скоростью движущиеся в ту же сторону, что и частицы неба, сильнее других стремятся удалиться от этого центра".
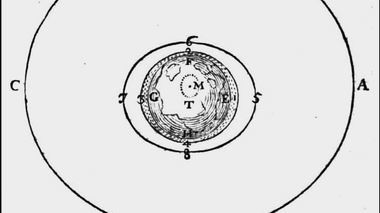
Фрагмент другого аналогичного рисунка."...За пределами круга ABCD нет никакого пустого пространства, в которое могли бы проникнуть частицы неба, находящиеся внутри этого круга, и притом продвинуться так, чтобы их место не заняли тотчас же другие, совершенно подобные им. Точно так же и частицы Земли не в состоянии удалиться от центра Т на большее расстояние, чем они от него удалены ..."
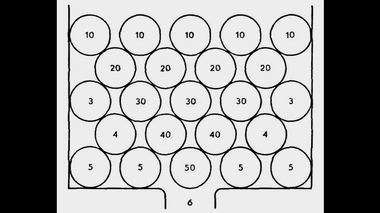
Разъяснения Декарта о перемещении частиц эфира:
"...и притом продвинуться так, чтобы их место не
заняли тотчас же другие, совершенно подобные им".
Когда рыба уплывает, частицы воды смыкаются и
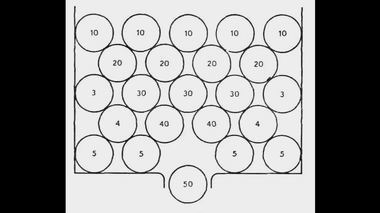
занимают ее место."... Ни одна из частиц, находящихся в равновесии, не может ни подняться, ни опуститься, если другая не сделает в тот же момент противоположного движения; всегда перевес на одной стороне сопровождается перевесом на другой. Например, камень R противостоит тому количеству воздуха (в точности равному ему по объему), которое находится над ним. Место этого воздуха он должен будет занять в случае, если он больше удалится от центра Т, а воздух этот должен обязательно опускаться по мере того, как камень поднимается".
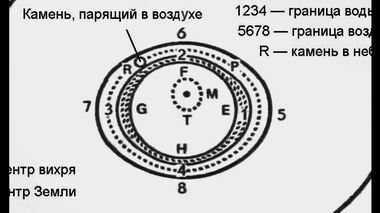
Камень R противостоит тому количеству воздуха, которое находится над ним."... Вы видите, что каждая частица земных тел придавливается к Т окружающей ее материей, но не безразлично всей, а только определенным количеством последней, совершенно равным величине частицы."
"... Хотя материя неба имеет больше силы для того, чтобы заставить камень R опуститься к Т, нежели для того, чтобы заставить опуститься туда же окружающий его воздух, она не должна иметь большей силы, чтобы толкать его перед собой с запада на восток. Следовательно, она не должна заставлять его двигаться в этом направлении быстрее воздуха".
По тем же причинам, по которым Луна вращается вокруг Земли по своей орбите, а камень по своей, будет вращаться и Земля вместе с Луной вокруг Солнца. " ... Материя неба должна вращать планеты не только вокруг Солнца, но и вокруг их собственного центра; образовать вокруг планет малые небеса, вращающиеся в том же направлении, что и большое небо."

По Декарту, вращение Земли вокруг Солнца происходит
точно так же, как и вращение Луны вокруг Земли.
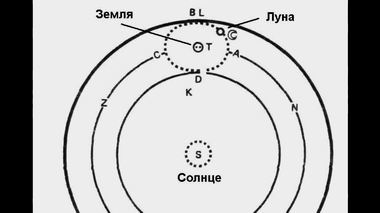
Луна вращается вокруг Земли в пределах малого вихря.
Этот малый вихрь вращается в пределах
большого вихря вокруг Солнца.
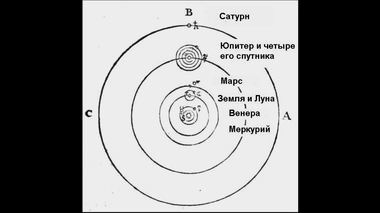
Аналогично происходит вращение всех планет и их спутников.
Спутники планет увлекаются малыми вихрями, а сами планеты
вращаются большим вихрям, в центре которого
находится вращающееся Солнце.Можно еще и еще цитировать Декарта, но вряд ли кто-нибудь сегодня поверит в работу его "сепаратора". Автор десятками способов пытается убедить читателя в успешной работе вихревого механизма. Чувствуется, что именно для выполнения этой задачи он придумал деление эфирной материи на три различных элемента.

Декарт десятками способов пытается убедить
читателя в работоспособности вихревого механизма.Кстати сказать, термином "эфир" Декарт воспользовался, как мне кажется, не более двух десятков раз. В "Трактате о свете" и в первых двух частях "Начал" он мне не попадался ни разу. Впервые он употребил его, кажется, в 100-м параграфе третьей части, состоящем из одного небольшого абзаца. В нем это слово прозвучало 3 раза. Столько же в 108 параграфе. В остальных случаях тоже наблюдается некоторая скученность использования данного термина.

Страница с параграфом 100.

Страница с параграфом 108.
Термином "эфир" Декарт воспользовался не более двух десятков раз.
Показаны две страницы из "Начал" Декарта с параграфами 100 и 108.Эфиром называлось всё: воздух и небо – чаще всего; правда, в качестве жидкости и третьего элемента он выступал редко. Философ не стремился к каким-то строгим дефинициям. Главным для него была тяга к ясности представлений. Но она-то, похоже, пострадала больше всего. Сколько ни вчитывайся, всё равно не понятно, почему Луна удерживается на своей орбите вокруг Земли, Или Земля и другие планеты вокруг Солнца.
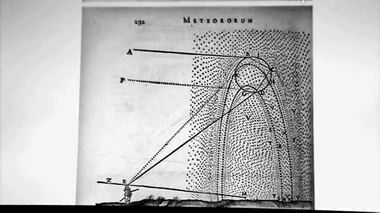
Страница из "Метеорологии" Декарта.Поэтому понять Ньютона можно, когда он заменил запутанные механизмы протискивания одних шаров сквозь груду других, действием одного-единственного импульса, который направлял движение небесного тела. Эту активную силу он ассоциировал, видимо, с импетусом, приписав инерции пассивную роль. Сам ли он придумал такой механизм, или где-то о нём прочёл, мы не знаем. Но в дальнейшей своей работе он от него никогда не отказывался.
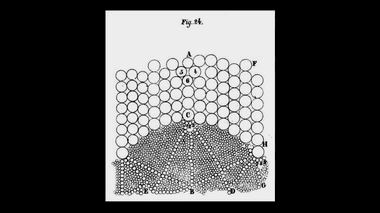
Понять Ньютона можно, когда он заменил запутанные механизмы
притискивания одних шаров сквозь груду других.Итак, Ньютон принял внешний импульс за импетус, а движение по стороне многоугольника как инерцию тела. Так как число сторон в динамической модели Ньютона стремится к бесконечности, а длина каждой стороны стремится к нулю, то можно считать, что инерция тела в точности соответствует импетусу. Таким образом, активное и пассивное начала кругового, эллиптического, параболического и любого другого криволинейного движения здесь неразличимы. Инерция и импетус, по мнению Ньютона, это две стороны одной медали. Отсюда вытекает та двойственность понятий, на которую мы выше указывали, и на которую впервые, по-видимому, обратил внимание Ричард Вестфолл.
Упрощенная Ньютоном вихревая модель Декарта.
Он принял внешний импульс за импетус, а движение
по стороне многоугольника за движение по инерции.
Только подобных чертежей Ньютон не вычерчивал;
слов импетус и инерция старался избегать.Как сказал Кёртис Уилсон (Curtis Wilson) в предисловии к книге Даны Денсмор (Dana Densmore). "Начала" Ньютона, несомненно, являются самой известной, но непонятой (в оригинале "непрочитанной" – "unread") книгой в западном мире. Денсмор – одна из немногих, кто правильно прочитала и адекватно интерпретировала великого путаника. С "Математическими началами натуральной философии" Ньютона 1687 года произошло примерно то же самое, что и с "Электродинамикой движущихся тел" Эйнштейна 1905 года. Никто как следует не разобрался в этих двух работах, но все сделали вид, будто всё поняли и стали на все лады прославлять имена авторов.


Дана Денсмор и ее муж Уильям Донахью, которые
перевели ньютоновские Начала адекватным образом.Что было до Декарта, мы пока не рассматривали; считаем отцом-основателем научного подхода к физике именно его, Картезия. Он предложил эфирно-вихревую модель, с которой трудно согласиться, но которая странным образом стала возрождаться сегодня. В следующей, пятой по счету, части нашего нескончаемого сериала мы собираемся рассказать о космических вихрях, пока что лишенных какой-либо определенной теоретической подкладки.

Маяк эфирного буйства

Талисман вихревой стихии.Оговоримся, слово "эфир", под которым идет сериал, служит нам маяком и своеобразным талисманом в анализе старых и новых физических теорий. Если смотреть на историю физики издалека, можно отчетливо видеть два позитивных и два негативных всплеска. Учение Декарта, несомненно, было положительным, но его торпедировал Ньютон, пришедший как будто из Средневековья, который предложил формально-геометрический подход, породивший множество вопросов. Затем Фарадей и Максвелл нарисовали новую прекрасную эфирно-вихревую картину мира, которую торпедировал софист Эйнштейн. И вот на горизонте засверкали лучи третьего позитивного мироздания. Надеемся, наступит день, когда явится гений и одарит человечество неведомым пока позитивным знанием.

Картезианец Лейбниц

Картезианец Гюйгенс
Все выдающиеся физики эпохи Ньютона
так или иначе склонялись к картезианству.У физиков континентальной Европы, прежде всего, Лейбница и Гюйгенса, которые придерживались эфирно-вихревых взглядов Декарта, в отношении Ньютона прозрение наступило быстро – сразу после внимательного прочтения первого издания "Начал" 1687 года. До выхода второго издания в 1710 году Иоганн Бернулли – тоже поклонник Декарта – опубликовал работу, в которой указал на принципиальную ошибку в сочинении Ньютона. В чём она состоит?
Иоганн Бернулли в 1710 году выявил в
"Началах" Ньютона принципиальную ошибку,
которая перечеркивает заслуги автора.Все, наверное, помнят, какую задачу поставил Роберт Гук перед Ньютоном. Тем, кто забыл, напомним. Секретарь Лондонского Королевского общества в качестве примирительного жеста – до этого у него с Ньютоном был нелицеприятный спор на почве теории света и цвета, закончившийся их ссорой – так вот, секретарь просил Ньютона математически доказать справедливость следующего положения.
Если центральная сила, действующая на небесное тело, убывает с квадратом расстояния – это, собственно, суть всемирного закона тяготения, предложенного Гуком тогда еще в качестве гипотезы – то, продолжаем, орбитой тела будет являться одно из конических сечений – эллипс, окружность (это частный случай эллипса, когда обе полуоси одинаковые), парабола (это тот же эллипс, у которого одна из полуосей уходит в бесконечность) или гипербола (она получается в том случае, когда тело попадает в поле действия центральной силы, но не захватывается им, а только искривляет его инерционное прямолинейное движение).
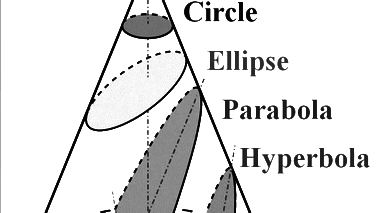
Конические сечения
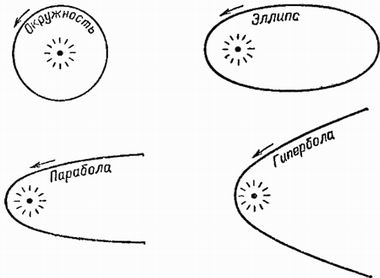
Окружность, эллипс, парабола и гиперболаТеперь открываем "Начала" Ньютона, книгу 1, отдел 3, предложение 11 (оно же, задача № 6); читаем в переводе Крылова: "Тело обращается по эллипсу; требуется определить закон центростремительной силы, направленной к фокусу эллипса". Вычерчивается эллипс, проводится касательная к точке P, где находится тело (любая планета), строятся так называемые "леса", т.е. вычерчиваются какие-то вспомогательные линии, и доказывается сформулированное предложение.
Дальше все повторяется, слово "эллипс" заменяется "гиперболой". Так, по индукции, появилось предложение 12 (или, задача 7). Наконец, формулируется предложение 13 (задача 8) в отношении параболы. Таким образом, Ньютон верен себе. Помните, как он в третьей книге "О системе мира" формулировал предложение 1 (или теорему 1): "Силы, которыми спутники Юпитера постоянно отклоняются от прямолинейного движения и удерживаются на своих орбитах, направлены к центру Юпитера и обратно пропорциональны квадратам расстояний до этого центра".

Бритва Оккама

Класс симпатичных кошечекРовно так же, он формулирует предложение 2 и 3, но уже в отношении планет Солнечной системы и Луны – спутника Земли. Спрашивается, зачем множить сущности без надобности, как говорил Оккам? Ведь всем ясно, что предложение – одно, которое касается различных объектов. Сегодня таких объектов сотни или даже тысячи и что – каждому из них посвящать отдельную теорему? Разумеется, нет. Любые теоремы всегда предполагают некую общность, которая затрагивает какой-то класс различных объектов.
В принципе, это относится к проявлениям симптомов шизофренического сознания Ньютона. К этому психическому расстройству, в частности, можно отнести и странную любовь Ньютона к получению результатов арифметических расчетов с умопомрачительной точностью. Такая точность не нужна, так как исходные данные, полученные, например, из астрономических наблюдений или физических экспериментов, изначально имеют низкую точность. Возможно, здесь нет никакой патологии. Есть ведь люди, которые целыми днями строят дворцы, крепости и города из спичек.

Любовь Ньютона к получению результатов
расчетов с умопомрачительной точностью.Подобное занудство совершенно несвойственно для творчески мыслящих людей. Ньютону тоже можно было бы простить схоластическую форму подачи материала. Но оказалось, что за этой дымовой завесой автор протаскивает очень сомнительные утверждения. Так, за тремя первыми предложениями третьей книги следовало четвертое, которое нас сильно озадачило.
Напомним, о чём оно: "Луна тяготеет к Земле и силой тяготения постоянно отклоняется от прямолинейного движения и удерживается на своей орбите". "Стоп!" – сказали мы себе. В отношении Луны и Земли действуют две составляющие: равноускоренная, направленная вертикально вниз, к центру Земли, и инерционная составляющая, направленная по касательной к орбите. Так как об инерционной составляющей теорема IV умалчивала, мы стали разбираться: а как, собственно, Ньютон представляет себе вращение Луны вокруг Земли. На этом пути пришли к Декарту, которого Ньютон в зрелые годы очень не любил.
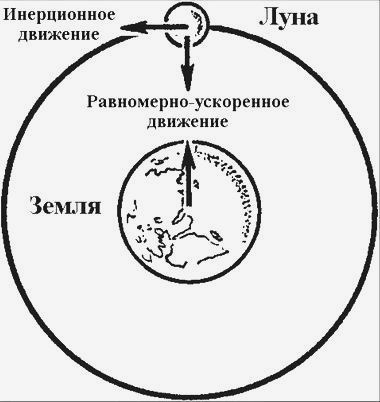
Две составляющие – радиальная и тангенциальная.Похожий случай произошел, видимо, и с Иогенном Бернулли в далеком 1710 году. Он внимательно прочитал предложения XI, XII и XIII. После XIII предложения шло следствие I, в котором говорилось: "Из последних трёх предложений следует, что если какое-нибудь тело выходит из места P по направлению прямой PR с какой-нибудь скоростью и находится под действием центростремительной силы, обратно пропорциональной квадратам расстояний до центра S, то тело будет двигаться по коническому сечению, коего фокус лежит в центре сил, и наоборот [contra]".
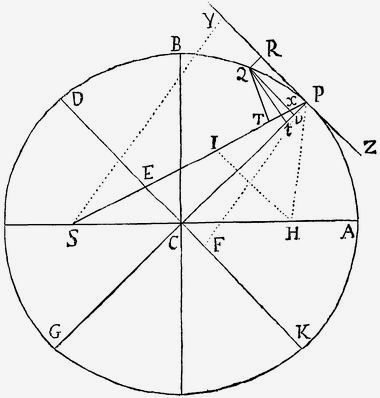
Чертеж эллипса к предложению XIII и следствию I."Стоп!" – сказали себе Бернулли. Если доказано, что тело, движущееся по какому-либо коническому сечению, под действием центростремительной силы, убывающей с квадратом расстояния, это вовсе не значит, что, задав скорость, направление и расположение тела относительно центра силы, можно указать форму орбиты. Обратная задача не вытекает из прямой – её нужно решать отдельно. Аргумент Бернулли был услышан Ньютоном и во втором издании "Начал" к следствию I он приписал несколько фраз.
Они свидетельствовали, что обратная задача решается однозначно, если решена прямая: "... ибо (добавление) при заданных: фокусе, точке касания и положения касательной можно построить лишь одно коническое сечение, имеющее в этой точке заданную кривизну. Кривизна же найдется по заданной скорости и известной центростремительной силе. Под действием той же центростремительной силы и при той же скорости не могут быть описываемы две различные орбиты, касающиеся друг друга".
С таким разъяснением противники ньютонеанцев не согласились. Они целиком отвергли архаичные рассуждения, используемые автором "Начал", и пошли по проложенному Лейбницем пути. Последний, как известно, претендовал на первенство открытия интегрально-дифференциального исчисления. Но его дискуссия с Ньютоном выявила более глубокие расхождения в математических подходах решения физических задач, чем банальный спор типа кто первый сказал "А".
Страница из сочинения Барроу.

Именно Барроу доказал формулу Ньютона – Лейбница
сложным геометрическим способом.Геометрический подход Ньютона, взятый на вооружение у его учителя Барроу, не обладал необходимой степенью общности. Автор "Начал" пытался решить одну-единственную задачу, заранее зная на нее ответ, т.е. занимался, собственно, банальной подгонкой под известный результат. Бернулли же, следуя по пути, впервые прочерченном Лейбницем, написал дифференциальное уравнение движения материального тела в общем виде, проинтегрировал его и, таким образом, получил все, какие только могут быть кривые, вид которых зависит от начальных и граничных условий конкретной задачи.
[В видеофильме показывается текст из книги:
В. И. Арнольд. Гюйгенс и Барроу, Ньютон и Гук — первые шаги математического анализа и теории катастроф, от эвольвент до квазикристаллов — М.: Наука. Гл. ред. физ.-мат. лит. — 1989. — 96 с. — ISBN 5-02-013935-1.]§ 6. Доказал ли Ньютон эллиптичность орбит?
В заключение рассказа о законе всемирного тяготения стоит сказать несколько слов о дискуссии, которая развернулась вокруг него в самые последние годы в физических журналах. В прошлом такая дискуссия была бы невозможной, но теперь ситуация изменилась благодаря тому, что дух современной математики проник и в ряды физиков, нанеся им, как это сейчас станет ясно, некоторый ущерб. Они начали сомневаться в таких вопросах, о которых раньше никто бы и разговаривать всерьёз не стал. В этой дискуссии приняло участие большое число физиков (отчёт о ней можно прочесть в одном из выпущенных недавно сборников «Физика за рубежом»10, а тема спора формулировалась следующим образом: доказал ли Ньютон, что из закона всемирного тяготения следует первый закон Кеплера?
В действительности, речь идёт вот о чём. Для траектории движущегося под действием силы тяжести тела законы Ньютона дают дифференциальное уравнение
dr/dt = – kr/r³
Вместо того чтобы решать его по всем правилам науки, Ньютон в своей книге предъявил много решений этого уравнения и проверил, что для любого начального условия среди них имеется удовлеворяющее ему решение. Иными словами, для любой точки и вектора в пространстве во множестве найденных Ньютоном орбит найдётся такая, которая в начальный момент проходит через эту точку и имеет там данный вектор скорости. При этом, если начальная скорость тела не слишком велика, то орбита получается эллиптической. Но кто сказал, спрашивают искушённые в математических тонкостях физики, что не существует какой-нибудь другой траектории, удовлетворяющей тем же самым начальным условиям, по которой тело движется, соблюдая закон всемирного тяготения, но совершенно иначе? Математики знают, что отсутствие такой другой траектории называется теоремой единственности. Таким образом, чтобы выводить из закона всемирного тяготения, что тела движутся так, а не иначе, Ньютону надо было не только предъявить много решений дифференциального уравнения, но и доказать для него теорему единственности. Доказывает он её? Нет. Ну, тогда и пользоваться этим законом для описания действительности тоже, вообще говоря, нельзя, пока не доказана теорема единственности. Кто это сделал первым? Иоганн Бернулли. Значит, это он, а не Ньютон, вывел закон Кеплера из закона всемирного тяготения, ему и должна принадлежать вся слава. Вот как говорят физики, участвовавшие в дискуссии, повторяя давно сказанное математиками (например, в книге А. Винтнера 1941 года)".
Метод Лейбница – Бернулли, но никак не метод Барроу – Ньютона, был усвоен Леонардом Эйлером и продвинут далеко вперед сначала в его двухтомной "Механике" 1736 года, а после во множестве его работ, которые были написаны с позиции декартовского мироощущения. Они навсегда похоронили жалкие потуги Ньютона дать миру универсальный метод для решения всех насущных задач механики. Система дифференциальных уравнений в частных производных Навье – Стокса, эфирные модели Коши и усовершенствованная им интегрально-дифференциальной методика Эйлера полностью сняли проблему обоснованности найденных в рамках матанализа решений.

Барроу и Ньютон

Лейбница и Бернулли

Леонард ЭйлерНо в этом месте мы вынуждены прерваться. Претензии картезианцев Лейбница, Бернулли, Гюйгенса, Эйлера к схоласту, алхимику и богослову Ньютону важны и обширны, но находятся несколько в стороне от выбранной нами стези. По этой же причине мы здесь не касаемся Гука, Флемстида и прочих спутников, которые, к своему несчастью, оказались на одном жизненном пути с Ньютоном. Наша задача продиктована удивительной находкой Ричарда Вестфолла, откопавшего следы эфирно-вихревой теории Декарта в главном сочинении Ньютона.
Давайте оставшееся время посвятим вопросу, как автор "Начал" математически совместил свои ранние идеи о вихревом движении Солнечной системы, которые он перенял у Декарта, с более поздней динамикой, регулируемой тремя законами Кеплера и законом всемирного тяготения Роберта Гука. С этой целью мы обратимся к доступной в Интернете книге Брюса Бракинриджа "Ключ к динамике Ньютона"; второе название этой книги "Задача Кеплера и Начала Ньютона". Она вышла в год смерти "Сэма" – так друзья называли Ричарда Самуэля Вестфолла, который умер от сердечного приступа в 1996 году. Но прежде зададим тон нашему повествованию.

Брюс Бракинридж: "Ключ к динамике Ньютона" или
"Кеплеровская задача и ньютоновские Начала."Задолго до выхода в свет книги Never at Rest в 1980-м году Вестфолл в журнале Science за 1973 год (том 179) опубликовал статью Newton and the Fudge Factor (Ньютон и фадж фактор). Можно перевести название этой статьи на академический манер, как Ньютон и фактор вероятности. Но слово фадж несет множество неприятных коннотаций: чушь, вздор, враньё, ерунда, гоупость и т.д. В "Началах" Ньютона наряду с фараоновской серьезностью, просматривается какое-то пренебрежение к читателю, что передается словами "валять дурака", или более современным термином "троллить". Вот это надо иметь в виду, когда читаешь Ньютона.
К этому добавим, что дальнейшая судьба "Начал" нас сейчас волновать не будет. Мы также намеренно избегаем темы, связанной с Гуком, Флемстидом и прочими спутниками, которых Ньютон, к их несчастью, повстречал на своем жизненном пути. Мы намерены дать в руки читателю "Ключ к динамике Ньютона", который смастерил Брюс Бракинридж.
[Титры и фото, сопровождающие предыдущие кадры]

Раньше мы упомянули имя Даны Денсмор (Dana Densmore).
Она в месте с мужем Вильямом Донахью (William Donahue)
написала книгу под названием:"Начала Ньютона, Центральный аргумент:
перевод, примечания, расширенные доказательства"
"Newton's Principia, The Central Argument:
Translation, Notes, Expanded Proofs".
Эту книгу хвалили главные ньютоноведы: Вестфолл, Бракинридж и Гвиччардини.
Наверное, можно было бы рекомендовать ее к прочтению.
Но лично меня настораживает одно обстоятельство.
Дана Денсмор серьезно увлечена суфийской традицией,
алхимией света, слушает священные звуки и т.д.
Что такое суфийский орден, которому принадлежит Дана?
Мне показалось, что это собрание сумасшедших людей.
"Приходите к нам, – призывает Дана,
пытливых умом, ищущих приключений
— чтобы погрузиться в неистовые и
красивые пространства".
Дана Денсмор и Говард Фишер.
Говард – учитель медитации с 30 летним стажем.
Он музыкант, который стремится пробудить в человеке
тонкие центры энергетического тела для
использования их в духовной закалке.Я исповедую рационализм –
единственно верное мировосприятие.Поэтому не стану рекомендовать книгу,
написанную автором с таким экзальтированным
сознанием, как у Даны Денсмор.В начале книги он приводит фразу, брошенную каким-то прохожим, увидевшим Ньютона, который проходил по улице вблизи Кембриджа: "Вот идет человек, написавший книгу, которую никто не смог прочитать". Примерно так, говорили и до сих пор говорят о теории относительности, которую никто до конца так и не понял. Марк Твен о ньютоновских "Началах" как-то заметил: "Каждый намеревается их прочесть, но никто не может заставить себя засесть за чтение".

Теорию относительности никто до конца так и не понял.Бракинридж не советует приступать к изучению "Начал" с третьего окончательного издания 1726 года – самого распространенного и доступного. Оно содержит множество переделок, изменений и дополнений, которые смазывают сравнительно прозрачное содержания первого издания этого сочинения, не говоря уже о наброске 1684 года, появившегося вскоре после общения Ньютона с Робертом Гуком в 1679 году.
Бракинридж предупреждает читателя, что Ньютон имел привычку добавлять новый материал в давно написанный им текст, так что последовательность изложения у него постоянно прерывается и становится практически непригодной к систематическому чтению. Уже в предисловии к первому изданию автор извиняется за такие не к месту приведенные вставки. В эскизном наброске 1684 года Ньютон передает одну единственную идею, навеянную Гуком. Ее содержание изложено в самой первой теореме, которая дает решение прямой задачи эллиптического движения тела. В первом варианте книги, вышедшем в 1687 году, к этой хрупкой кости Ньютон приращивает жирные куски мяса, скрывшие естественный блеск кости.
После публикации первого издания он радикальным образом меняет стратегию решения кеплеровской задачи. В отличие от одного метода динамического анализа, изложенного в первом издании (назовем его гуковским) проявляются еще два альтернативных метода, которые можно было бы назвать декартовским и галилеевским. Эти альтернативные положения вставлялись между старыми положениями первого издания, что называется, без всяких опознавательных знаков. Ньютон не давал никаких разъяснений. Читатель мог видеть, что какое-то положение доказывается одним способом, затем другим, иногда, может быть, и третьим. Правда, не ко всем положениям первого издания Ньютон придумал два соответствующих альтернативных положения, так что в итоге получился винегрет из разнородных элементов, имеющих различные теоретические основы. Дело усугублялось тем, что немалая часть теорем, предложений и задач осталась на страницах его черновиков в недоделанном виде, которые так и не увидели свет.
В результате этой скрытой умственной работы появилось несвязанное сочинение, имеющее странное деление на подразделы. Уже в первом издании мы сталкиваемся с заголовками типа: "Предложение IV. Задача IV". Далее идет "Схолия" (т.е. "Поучение" – это схоластический термин). Сразу же за Схолией идет пункт, озаглавленный: "Предложение V. Задача I". За ним идет следующий, озаглавленный "Предложение VI. Теорема V". Никакой логики в этих названиях не просматривается.
По-видимому, "двойная бухгалтерия" возникла из-за спонтанно возникших утверждений, появлявшихся в разное время долгой жизни Ньютона, которые получали достаточно случайные наименования – просто чтобы их можно было как-то различать. Бракинридж считает, что в будущих изданиях Ньютон надеялся избавиться от этой "дойной бухгалтерии", но до этого руки не дошли, поскольку он так и не сумел сгруппировать материал в какую-то стройную цепочку утверждений. В итоге, всё его необъятное сочинение выглядит сырым, незаконченным и неудобоваримым, как "Капитал" Маркса (думаю, марксисты оценят это сравнение).

Ньютон в молодости в представлении неизвестного художника.С юных лет Ньютон был очарован красотой кеплеровских законов, и уже в стенах Кембриджского университета стал усиленно искать силу, вызывающую эту красоту. Естественно, он сразу натыкается на популярное в его время учение Декарта, которому был беззаветно верен без малого два десятка лет, пока Гук не вызволил его из картезианского плена.
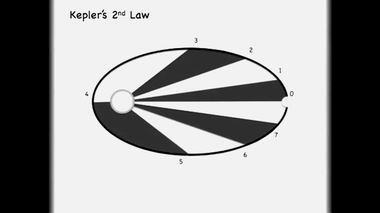
Красота кеплеровских законов.По пути от Декарта к Гуку Ньютон успел восхититься Галилеем. Он чувствовал, что параболический закон движения пушечного ядра, о чем неустанно говорил итальянский бунтарь, эллиптическая форма планетных орбит и круговой закон движения вихря вызваны одной универсальной силой. Поэтому он попытался в своих "Началах" соединить идеи Кеплера, Декарта, Галилея и Гука в одну стройную геометрическую теорию – таков был его тайный замысел. Увы, ему не суждено было сбыться.

Параболический закон движения пушечного ядра,
открытие которого приписывается Галилею.Ньютон всегда считал себя геометром, прилежным учеником геометра Исаака Барроу. Рациональными проблемами физики он интересовался в последнюю очередь. Его голова была забита средневековой алхимией, астрологией и какими-то религиозно-мистическими глупостями, о которых в его время стыдно было признаться. Следовать принципу дальнодействия он стал неосознанно, поскольку не знал и ничего знать не хотел о строении мировой среды. Короткий век "Начал" объясняется именно тем, что автор был никудышным физиком.

Голова Ньютона была забита средневековой
алхимией, астрологией и прочими глупостями.До переписки с Гуком в 1679 году, Ньютон оперировал понятиями Декарта и Гюйгенса о центростремительных и центробежных силах, появляющихся в крутящихся системах. Ньютон рассматривал круговое движение как равновесное состояние этих двух противостоящих сил. Гук, напротив, считал круговое движение неравновесным. Он заявил о действии закона всемирного тяготения, играющего роль центростремительной силы, и о законе инерции, взявшего на себя функцию центробежной силы. Неуравновешенная сила постоянно отклоняет тело, которое в противном случае продолжило бы движение по прямой. Именно эта гуковская идея превратилась в теорему № 1 и сделала "Начала" книгой № 1 классической физики.

Ньютон считал круговое движение равновесным, т.е.
когда центростремительная и центробежная силы равны.
В этом случае Солнце не притягивает Землю; она сама
кружится в вихре – Солнце может отсутствовать.
Это – декартовское движение.

Гук считал круговое движение неравновесным, т.е.
когда движение по инерции заставляет Луну улететь
вдаль, но Земля тянет ее обратно к себе.
Это – гуковское движение. Ньютон
не различал эти движения.
Эту ясную гуковскую идею Ньютон разбавил туманными спекуляциями вроде того, что радиальное смещение к центру потенциально может быть вызвано внешней силой, которая не реализована в связи с действием внутренней силы. Ясно, что в этой схоластике автор желает протащить модель, навеянную движением вихря, но в более поздней формулировке он эту декартовскую схему сближает с гуковской; говорит, что радиальное смещение к центру может быть фактически внутренним, оно-то и реализуется.

Внутренние силы

Внешние силы
Ньютон спекулировал на смутных понятиях внутренней и внешней силы.Таким образом, с точки зрения физики, анализ движения планеты по орбите вокруг Солнца смахивал на спекулятивные рассуждения какого-нибудь средневекового схоласта. Но с точки зрения чрезмерно гибкого, можно сказать, резинового, геометрического метода Ньютона, который предстал перед читателем в трех ипостасях (гуковском, декартовском и галилеевском), всё выглядело достаточно пристойно. Так, используя декартовскую аппроксимацию (т.е. приближение), Ньютон легко доказывал справедливость второго закона Кеплера.

Ньютон часто рассуждал в духе средневековых схоластов.
Есть историки, которые пытаются понять, как Ньютон представлял эфир.
Бессмысленное занятие! На сей счет у него не было определенного образа.
В его текстах найдется десяток противоречивых представлений этого объекта.Если тело движется под действием серии импульсных центростремительных сил, то оно описывает равные площади за равные промежутки времени. Площадь заштрихованного полигона сведется к площади под дугой эллипса, когда время между внешними импульсами (считай, импетусами) сократится до нуля, а число сторон полигона приблизится к бесконечности.
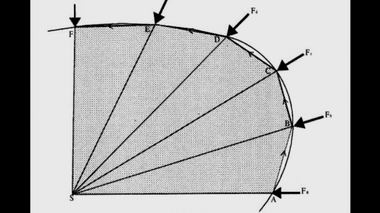
Аппроксимация линии эллипса сторонами полигона;
это называется декартовским приближением орбиты.Используя гуковскую аппроксимацию, Ньютон так же легко доказывал справедливость этого же закона. Он вычерчивает похожий чертеж, где площадь под дугой эллипса разбивалась на равные площади треугольников. Если число треугольников устремить к бесконечности, то справедливость второго закона Кеплера будет доказана. Наряду с этими двумя аппроксимациями, где используются многоугольники, Ньютон разработал ещё одну, галилеевскую, где использовалась приближенная гладкая кривая.
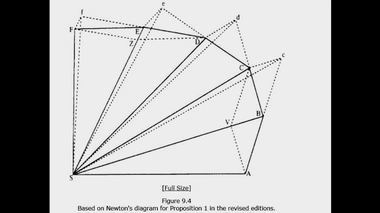
Аппроксимация линии эллипса сторонами полигона,
построенного на основе неравновесной динамики Гука;
это называется гуковским приближением орбиты.Галилей показал, что движение тела в соответствии с постоянным ускорением имеет следующие атрибуты. Во-первых, пройденный путь пропорционален квадрату времени; во-вторых, это ускоренное движение может быть совмещено с равномерным движением по прямой и, в-третьих, сочетание обоих движений приводит к параболической траектории. Закон Галилея о зависимости пройденного пути от квадрата времени отображены в "Началах" в лемме 10, в следствии к ней и в предложении 6.
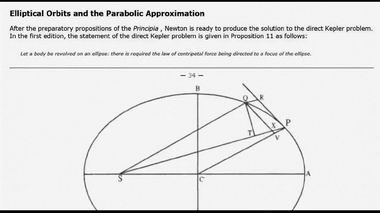
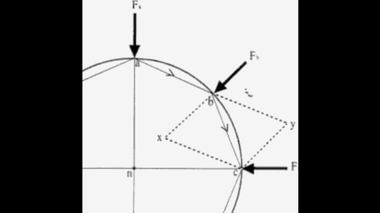
Аппроксимация линии эллипса множеством отрезков параболы;
это называется галилеевским приближением орбиты.Параболическое приближение предполагает, что в самом начале движения тела сила в любой точке заданной кривой примерно постоянна. Таким образом, сочетание исходной тангенциальной скорости и ускорения за счет постоянной силы приводит к исчезающе малой дуге параболы, что служит элементом аппроксимации общей кривой в данной точке. Не используя свойства параболы в явном виде, Ньютон берет за величину силы радиальное смещение, которое обратно пропорционально квадрату времени.
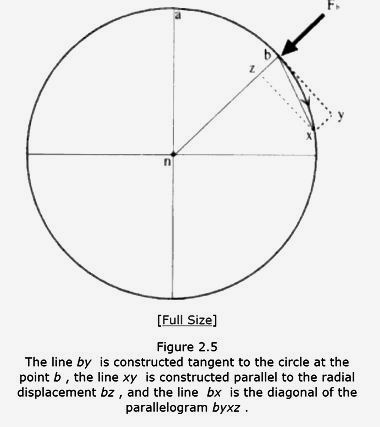
Галилеевская или параболическая аппроксимация круговой орбиты.На этом чертеже показана третья, галилеевская аппроксимация. Линия by строится как касательная к точке b, линия xy построена параллельно радиальному смещению bz, а линия bx является диагональю параллелограмма byxz. Таким образом, Ньютон аппроксимирует элемент окружности в окрестности точки b элементом параболы. Далее, используя все три типа аппроксимации, Ньютон переходит к решению прямой задачи Кеплера тремя способами. Правомерность такого геометрического подхода к решению физической задачи была оспорена разработчиками дифференциально-интегрального исчисления, живущими в континентальной Европе – Лейбницем, Гюйгенсом, Бернулли, Эйлером, Коши и прочими приверженцев эфирно-вихревого мировоззрения Декарта.
Параллельный (к основному) текст и фотографии

Никкола Гвиччардини – знаток математического наследия Ньютона.
Он автор книги "Исаак Ньютон. Математическая точность и методика".

Книга получила широкое признание в узких кругах ньютоноведов.
Персональный сайт Гвиччардини.
Титры читать неудобно, когда одновременно читают другой текст.
Поэтому нажмите на "паузу" и прочтите нижеследующее.
Начало Предисловия книги Гвиччардини"Нет никаких сомнений в том, что Исаак Ньютон является одним из наиболее исследованных гигантов научной революции. Мало сказать, что он был математиком уровня Архимеда и Карла Фридриха Гаусса. Историки математики посвятили огромное внимание его работам по алгебре, рядам, флюксиям [дифференцированию], квадратурам [интегрированию] и геометрии. В частности, после публикации восьми томов Математических работ (1967 – 1981) под редакцией Д.Т. Уатсайда, любой заинтересованный читатель имеет доступ к многогранному вкладу Ньютона в математику. Эта книга не собирается конкурировать с этой сокровищницей информации. Я, скорее, сосредоточился на одном лишь аспекте математической работы Ньютона, который до сих пор остается не освещенным, а именно, на математической философии Ньютона. Основной вопрос, который мотивировал данную книгу, можно сформулировать так: чем была для Ньютона математика?"
Примечание
Гвиччардини назвал имя Уатсайда (D.T. Whiteside) и его труд 1967 - 1981, который разбит на три части: 1) исследования по флюксиям и бесконечным рядам; 2) прочие исследования; 3) исследования по геометрической оптике. Эти три части размещены по восьми томам:
т. 1. 1664 – 1666, т. 2. 1667 – 1670, т. 3. 1670 – 1673, т. 4. 1674 – 1684,
т. 5. 1683 – 1684, т. 6. 1684 – 1691, т. 7. 1691 – 1695, т. 8. 1697 – 1722.Гвиччардини, как было сказано в Предисловии, не собирается соревноваться Уатсайдом в полноте освещения ньютоновского наследия. Его задача – уловить философские истоки деятельности "островитянина". Несомненно, это превосходная, важная и своевременная цель для историка науки. Но у меня сложилось устойчивое предубеждение, что автор "Математических начал натуральной философии" не тот математик, геометр или натур философ, сочинения которого заслуживают кропотливого изучения.
Уже не раз говорилось, что Ньютон не был самостоятельным исследователем и не произвел на свет сколько-нибудь оригинальных методик. Всё обилие и разнообразие его работ объясняется старательным собиранием идей у других независимых ученых. Сравнивать его с Архимедом и Гауссом, как это сделал Гвиччардини, значит, принизить масштаб двух последних гениев. Если историк науки делает такое выспреннее сравнение, то нам, рациональным скептикам, с ним не по пути. Впрочем, очень возможно, что здесь мы имеем дело с ничего незначащим реверансом смертного итальянца в адрес бессмертного англичанина.
Замечание
Нынешние историки восхищаются военными победами Александра Македонского. Меньший восторг вызывают успехи Наполеона. Чудовищные "подвиги" Гитлер осуждают все. Если бы Александр Македонский и Наполеон воевали во времена Гитлера, они бы тоже сели на скамью обвиняемых в Нюренбергском процессе. В наше время ими бы занялся Гаагский суд.
Сообщество ученых не имеет объективного и независимого судебного органа. На практике часто ссылаются на коллегию авторитетных экспертов. Иногда говорят неопределенно, вроде того, что время расставит всё по своим местам.
Увы, в отношении оценки научных заслуг того или иного исследователя господствует полнейший субъективизм. Вердикт сотни нобелевских лауреатов, скорее всего, окажется ошибочным. Деятельность какого-нибудь античного мудреца обрастает мифами, он превращается в человека-легенду, так что на справедливый суд истории тоже не приходится рассчитывать.
Единственным критерием служит практика – превращение теории в материальные предметы, стоящие на службе общества. Сегодня нас окружает множество технических устройств. Кто их изобрел – мы не знаем. Какие теоретические принципы лежат в основе их работы – мы тоже не знаем. Ученый является анонимом. Слава, известность – это ненужный побочный продукт человеческой жизнедеятельности. Он бесцеремонно вторгается в нашу жизнь, как навязчивая реклама.
Чем скорее мы забудем такие имена как Ньютон и Эйнштейн, тем спокойнее будет наша жить. Первым шагом на этом пути должен быть запрет на упоминание этих имен в стенах средней и высшей школы. Вторым – отмена научных званий, роспуск аттестационных комиссий всех уровней, включая Нобелевский комитет. Эти социальные институты питают нездоровое чувство тщеславия, которое находится в прямом противоречии с главным предназначением любого исследователя.
См. фильм с этим текстом
http://youtu.be/9oo4GpN32EQ