Эфир (Часть 6) Эффект Доплера

О.Е. Акимов

В предыдущей, пятой, части мы немного коснулись методов поиска экзопланет. Сказали, что космическая обсерватория на базе телескопа "Кеплер" использовала транзитный метод, который связан с прохождением экзопланеты по диску звезды. При этом интенсивность свечения диска слегка проседала. По характеру ослабления яркости можно судить о размерах экзопланеты и параметрах ее орбиты. Несмотря на скудость информации, транзитный метод на фоне ранее используемого метода Доплера, выглядел вполне достойно.

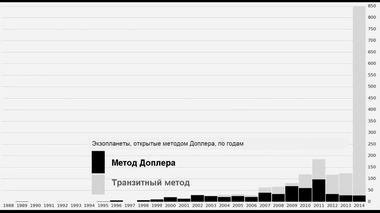
Транзитный метод дал результаты лучше, чем метод Доплера

Чтобы понять, почему транзитный метод дал результаты лучше, чем метод Доплера, нужно немного погрузиться в детали последнего. Внимательно понаблюдайте за этим вращением планеты. Видите, звезда слегка колеблется, так как вращение планеты происходит не точно вокруг центра звезды. Планета вместе со звездой вращается вокруг их общего центра массы. Но так как звезда обычно имеет большую массу по сравнению с массой планеты, то отклонение звезды едва заметно. В экзопланетных системах масса звезды и планеты часто сопоставимы. Что происходит в этом случае?

Линии спектра звезды сдвигаются вправо или влево
в зависимости от направления движения звезды

Планета и звезда вращаются возле общего центра тяжести. Таким образом, присутствие экзопланеты заставляет звезду слегка колебаться. Если она удаляется от наблюдателя, линии ее спектра сдвигаются вправо, т.е. в красную область; если звезда приближается к нам, спектральные линии сдвигаются влево, т.е. в фиолетовую область. Это позволяет судить о периоде и массе экзопланеты.

Этим объяснением мы и ограничились в предыдущей лекции. Так поступают многие — ведь идея метода, кажется, передана полностью. Апелляция к формулам только затемнит суть метода. Все доверяют математикам — вряд ли они что-то напутали. Настоящий скептик не должен никому доверять. Люди ошибаются в самых неожиданных местах, когда ситуация представляется абсолютно прозрачной.

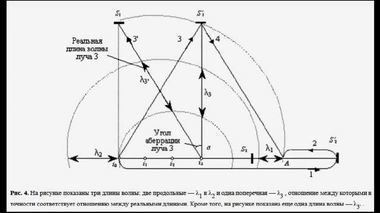
Майкельсон ошибся в угле наклона луча света,
который исходил из источника, установленного
на платформе движущегося интерферометра

Напомним ошибку Майкельсона в эксперименте по обнаружению эфирного ветра (в первой части этих видео-лекций мы подробно говорили об этом). Уважаемый экспериментатор ошибся в угле наклона луча света, который исходил из источника, установленного на платформе движущегося интерферометра. При этом, очевидно, Майкельсон ориентировался на пример с лодкой, которая при пересечении реки сносилась по ходу течения воды. Ровно так же он изобразил луч свет (номер 3), который отклонился по ходу движения прибора. На самом же деле, луч 3 отклониться влево, т.е. в противоположную сторону относительно движения интерферометра, установленного на поверхности Земли.

Теперь давайте посмотрим на формулы, которые используются в методе Доплера. С этой целью откроем соответствующую страничку, например, на популярном в нашей стране сайте "Астронет". Читаем: "Доплер эффект — это изменение частоты принимаемых волн при относительном движении источника и приёмника (наблюдателя). ... При увеличении расстояния между источником и приёмником период принимаемых колебаний увеличивается (частота уменьшается).

В случае эл.-магн. волн, распространяющихся в вакууме, принимаемая частота (в пренебрежении релятивистскими эффектами) равна:

Формула для случая эл.-магн. волн, распространяющихся в
вакууме, принимаемая частота равна выражению

Ф-ла (1) верна только при условии, что . При очень больших скоростях (v ~ c) необходимо учитывать релятивистские эффекты. ... Изменение частоты определяется только замедлением времени в движущейся системе отсчёта:

Изменение частоты определяется только замедлением времени

"Метод Доплера" часто называется "Методом измерения лучевой скорости". Поэтому открываем на сайте "Астронет" статью "Лучевая скорость". Читаем: " Лучевая скорость — это скорость изменения расстояния между объектом и наблюдателем. Метод определения лучевой скорости звёзд, галактик и др. астрономич. объектов основан на использовании эффекта Доплера. Л. с. определяется по смещению линий (излучения или поглощения) в спектре источника или по изменению частоты отражённого сигнала при радиолокации.

Выражение для нахождения скорости движения
звезды по величине отклонения спектральных линий

Это короткое разъяснение; в следующем абзаце дается простое математическое выражение для нахождения скорости движения звезды по величине отклонения спектральных линий, которые мы наблюдали только что на анимационном рисунке. Итак, читаем: " Если относительное изменение длины волны ... В близких к Солнцу окрестностях Галактики звёзды имеют Л. с. примерно от -100 до +240 км/с ...

Вот, собственно, и вся теория, связанная с "Методом эффекта Доплера" или "Методом измерения лучевой скорости". Сейчас приступаем к поиску ошибок физического и математического характера.

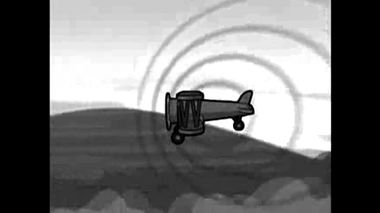
Взгляните на этот самолетик...

Взгляните на этот самолетик: впереди него волновые кольца прижаты друг к другу, позади него они разряжены, т.е. по ходу движения длина волны укорачивается, позади — удлиняется; с частотой наоборот: спереди самолета она выше, позади него — ниже. Из этого мультика нам всё это хорошо видно. Ну, а как быть с приемником? Если сближение источника и приемника происходит только за счет движения приемника, а источник покоится. Ситуация симметричная?

Нет, говорят нам знатоки, здесь есть нюанс. Если колебания акустические, как, например, гул самолетного двигателя, то движение источника и аналогичное ему движение приемника будут различаться.

Таблица 4.1

В таблице 4.1 представлены все 8 комбинаций, касающиеся источника i (меленькое) и приемника А (большое). Названный случай занимает первую строчку A i сближаются, причем приемник А движется, источник i покоится. В этом случае имеем для воспринимаемой волны. Если сближение идет за счет движения только источника (см. вторую строчку), то воспринимаемая длина волны равна ... Таким образом, акустические формулы для сближения источника и приемника будут отличаться.

Поясняющий текст

Для света же и других электромагнитных колебаний эти две ситуации абсолютно равноправны, так как в этом случае мы оказываемся на территории теории относительности. Для нее неважно, относительно чего движется — приемник относительно источника или источник относительно приемника; учитывается только разность скоростей.

Скептик

Минуточку, говорит скептик, а что, собственно, меняется для электромагнитных волн по сравнению с акустическими? В обоих случаях мы имеем дело с одинаковыми геометрическими чертежами. Оба типа волн изображаются правильными окружностями (на плоскости) или сферами (в пространстве), динамика их взаимодействия одинаковая. Среда есть среда и неважно, из чего она состоит — из воздуха, воды, металла или эфира. Если свет распространяется как-то иначе — покажите это. Наверное, картина интерференции акустических волн должна отличаться от световых? Но нет — геометрия одна и та же, никакой разницы.

Наверное, картина интерференции акустических волн должна
отличаться от световых? Но нет — геометрия одна и та же.

Сейчас мы подходим к самому любопытному явлению в истории науки. Ни античные софисты, ни средневековые схоласты никогда ничего подобного не говорили и не доказывали. Двадцатый век и вот уже полтора десятка лет века нынешнего, 21-го, в науке ничего подобного не происходило. Вы очень удивитесь, скажите "я что-то напутал", быть не может такого. Может! Еще как может. Сейчас вы сами в этом убедитесь, когда окажетесь перед совершенно тупиковой ситуацией. В чем она состоит?

Тупиковая ситуация

Вы видели таблицу 4.1. В ее справедливости невозможно сомневаться. Она демонстрирует восемь вариантов нахождения воспринимаемой длины волны или частоты, если движется только источник колебаний, только приемник, или то и другое вместе. Число вариантов увеличивается за счет направления скорости. Перед ней ставится либо плюс, либо минус. Любой школьник сможет получить эти нехитрые выражения, если не поленится. А теперь релятивисты вас ставят перед выбором: воспринимаемая длина волны или частота зависит только от разности скоростей.

Две верхнии строчки табл. 4.1.

"Как же так? — скажите вы. — У нас несколько формул попадает под этот релятивистский принцип относительности. Одна формула используется для случая, когда движется только источник, вторая, когда движется только приемник. Еще есть формулы, когда движется и то и другое вместе. Здесь нужно выбирать. Но с точки зрения теории относительности все варианты абсолютно тождественны. Возьмем для примера наши два ранее рассмотренные варианта по сближению источника и приемника: первая строчка формул записана для движения только приемника, вторая — только для движения источника. Господа релятивисты, если иметь в виду длину волны, то мне какой сейчас формулой следует воспользоваться, где 1 + β стоит в знаменателе, или вторым вариантом, где 1 – β стоит в числителе? Ответьте, пожалуйста.

Если эфирный ветер не был обнаружен в опыте Майкельсона,
это еще не значит, что его не существует.

То, что эти выражения различны, говорит об одном: эфир существует. Длина волны или частота будут различаться, когда движется источник относительно эфира, и когда движется приемник относительно эфира. Таким образом, в процессе распространения электромагнитных колебаний неподвижный эфир играет роль абсолютной системы координат. Эту роль берет на себя неподвижный воздух для звуковых колебаний. С точки зрения геометрии волн и математических выражений распространение звуковых и световых колебаний будет абсолютно одинаковым. Когда релятивисты выбросили эфир, якобы за его ненадобностью, поскольку он не был обнаружен в эксперименте Майкельсона-Морли, то, тем самым, они внесли в физику ужасную неразбериху, страшную путаницу. Как быть несчастному практикующему физику, какой формулой ему пользоваться?

И это притом, что мы находимся еще в самом начале пути. До сих пор рассматривались элементарные варианты Доплер-эффекта, когда направление излучения, векторы движения источника и приемника находятся на одной прямой. Когда движущийся источник проносится под прямым углом мимо приемника (наблюдателя), релятивисты заговорили о замедлении времени. Появился релятивистский радикал. Пусть так, но базой для релятивистских формул являются классические формулы. Значит, нам придется выбирать, какой классической формулой пользоваться.

Попытайтесь понять очень простую вещь. Релятивист пользуется какой-то одной релятивистской формулой (сейчас не будем говорить какой) для ситуации взаимного сближения источника и приемника. Вид формулы должен быть таким, что для нее нет никакой разницы, что относительно чего движется: приемник относительно источника, источник относительно приемник, а может быть, какой-то промежуточный вариант, когда и источник и приемник как-то перемещаются, что в итоге происходит их сближение.

Теперь представим себе, что все скорости плавно и строго пропорционально уменьшаются, так что все они становятся далеки от световых. Следовательно, ваша релятивистская формула должна точно также плавно переходить в классическую. Но какую классическую? Ведь их несколько: движется только источник, движется только приемник и потом еще несколько вариантов, когда оба они как-то перемещаются. Так возникает тотальная неопределенность. Переход от одной релятивисткой формулы к одной конкретной классической формуле сделать невозможно в силу возникающей неопределенности.

Слайд № 5

Смотрите, сейчас за кадром я говорю один текст. Он связан с таблицей 4.1. А видеофоном выступает слайд №5 с другим текстом на тему "Парадокс штриха в теории относительности". На минуточку прервем свое закадровое повествование, т.е. оторвемся от таблицы 4.1., чтобы сказать буквально несколько слов о тексте, фигурирующем в кадре. Читаем его:

"Если источник движется, приемник покоится, то длина волны (лямда 1) определяется выражением 8; если источник покоится, а приемник движется, имеем выражение 9. В формулах v1 и v2 — скорости источника и приемника относительно среды". Например, воздуха, то есть формулы 8 и 9 — классические. В них появляются косинусы с углами θ1 и θ2. Дальше, оставаясь в классической зоне, мы поговорим об этих косинусах, откуда они взялись, а пока продолжу чтение.

Классические формулы 8 и 9

"В теории относительности среда отсутствует, нет отдельных скоростей v1 и v2, но есть относительная скорость v, равная разности скоростей v1 и v2. Какой формулой нужно воспользоваться — (8) или (9), когда имеем дело с теорией относительности?" Данный вопрос касается неопределенности, о которой мы говорили только что, показывая таблицу 4.1.

"С точки зрения первого постулата об относительности движения источника и приемника мы можем с равным успехом записать две формулы 10а и 10б. В книгах, учебниках и справочниках по физике, например, "Справочник по физике" Яворского и Детлафа, "Оптика" Сивухина (эти две книги в нашей стране очень популярны, дальше), "Общая физика" Росселя, "Оптика движущихся тел" Франкфурта и Френка и т.д." В многочисленных моих текстах на тему парадокса штриха я привожу и другие книги, сейчас не станем на них отвлекаться. Продолжем дальше: "... можно найтис равной вероятностью и формулу 10а и формулу 10б".

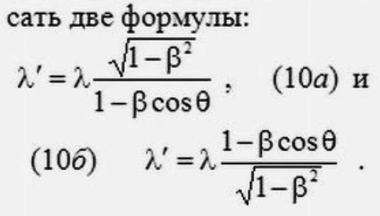
Релятивистские формулы 10а и 10б

В самом деле, в начале нашей лекции цитировался текст из статьи Доплер-эффект, взятый с сайта Астронет. В нём фигурировала формула 3 для частоты. В ней релятивистский радикал стоит в числителе. Значит, в формуле для длины волны числитель и знаменатель поменяется местами и окажется, что формула 3 соответствует формуле 10б на слайде №5.

Посмотрим, какой строчке таблицы 4.1 соответствует формула 3. Видим, что второй для случая, когда источник и приемник сближаются, причем приёмник покоится, источник движется. Но у нас есть еще одна интернетовская статья с релятивистской формулой для эффекта Доплера. В ней мы видим, что в знаменатели выражения фигурирует уже плюс, а не минус. При этом указывается: "Если источник радиально удаляется от наблюдателя, то θ = 0, если приближается — θ = π". В формуле стоит плюс, значит, она записана для θ = 0. В таблице 4.1 этот вариант формулы отвечает уже четвертой строчке.

Другая релятивистская формула

С математической точки зрения ошибок, как будто бы нет, но с точки зрения физики теории относительности здесь мы имеем большую головную боль. Зачем писать: "Если источник радиально удаляется от наблюдателя". Согласно ее постулату, сближение источника и приемника может происходить за счет движения только приемника (такое сближение равносильно сближению в предыдущем случае). Но этот второй вариант соответствует уже первой строке таблицы 4.1. Тогда релятивистская формула должна была выглядеть иначе, записываться одной строкой, без дробной черты. Аналогично для случая удаления приемника от источника за счет движения только источника (это соответствует третьей строке). В этом случае формула тоже записывалась бы одной строкой без дробной черты.

Теперь продолжим читать текст слайда №5 с того места, где прервались.

Парадокс штриха

"Это обстоятельство (т.е. неоднозначность выбора между формулами 10а и 10б) получило название парадокс штриха." Тут же я даю разъяснения, откуда он взялся. "Данный парадокс распространился на эталоны длины и времени. Так, Эйнштейн, Борн и Паули выражали изменение эталовнов длины и времени (приводятся выражения; здесь следите внимательно за штрихами, где они стоят); в курсе физики Ландау и Лифшица эталоны изменяются отднотипно: ... ; в Берклеевской "Механике" (выражения для эталонов времени и пространства изменяются неоднотипно); наконец, в курсе Левича (эталоны изменяются однотипно, но не так, как в курсе Ландау и Лифшица)". Теперь внимание! Во всех четырех выражениях штрихованная система движется, нештрихованная покоится.

Данная неоднозначность проистекает из неоднозначности вывода всех четырех выражений для эталонов длины и времени из формул прямых и обратных преобразований Лоренца.

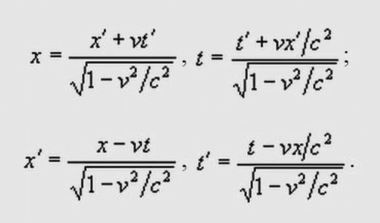
Формулы прямых и обратных преобразований Лоренца

В этом месте релятивисты начинают бунтовать и кричать: "Стоп, стоп, стоп! Покажите конкретно, кто, как вывел формулы для эталонов. Это вы сами запутались, не разобрались в исходном материале и теперь морочите нам голову".

Релятивисты не могут поверить в неоднозначность выражений, связанных с расстановкой штриха. Они, естественно, больше доверяют Эйнштейну и Ландау, чем какому-то чижику, которого никто не знает. Очень немногие имеют желание копаться во всем том мусоре, который остался после жизнедеятельности релятивистов. Те немногие, кто всё же решил выслушать мои разъяснения, через час-два — а времени на разбор деталей уходит не меньше — начинают зевать, внимание их притупляется, и они уходят с недоумением, хотя не всегда признаются в этом.

У нас нет сейчас времени на разбор релятивистских завалов. Одна их ошибка влечет другую, та цепляет третью и конца этому клубку противоречий найти очень сложно. Между тем, хотелось бы оставаться в теме эффекта Доплера и не растекаться мыслью по древу релятивистской физики. Поэтому тему парадокса штриха осветим по минимуму.

Открываем страничку с подразделом 5 "Парадокс штриха и парадокс лыжников". Пропустим начало, смотрим дальше: парадокс штриха "внес Эйнштейн в своей самой первой работе" 1905 года. Он написал формулу для частоты, "когда наблюдатель А движется со скорость v относительно бесконечно удаленного источника. В наших обозначениях имеем пару соответствующих формул:

Формулы Эйнштейна из работы 1905 года

По идее, он одолжен был написать второе выражение для движущегося источника и покоящегося наблюдателя. А потом третью формулу, когда и приемник, и источник перемещаются. Но общую формулу вот такого вида:

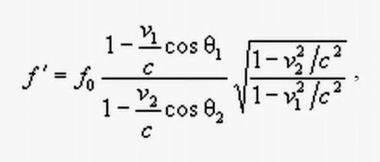
Формулы, которой не было у Эйнштейна

он так и не написал. Зато она появилась в статье Макса Лауэ. "Этот правоверный релятивист и не догадывался, какую мину, он подложил под теорию относительности. Теперь, согласно последней формуле, всякий желающий сможет точно установить, что именно движется относительно эфирной среды – приемник A со скоростью v1, источник i со скоростью v2 или и то и другое вместе". Позднее релятивисты отказались от логики Эйнштейна и Лауэ конкретно указывать, что относительно чего движется. Они стали брать разность скоростей источника и приемника. Тут же возникла путаница, которая обнаруживается при сравнении текстов указанных книжек.

Формула, которая появилась в статье Макса Лауэ

Парадокс лыжников тоже касается эффекта Доплера, но раскрывать его не будем, нет сейчас на него времени.

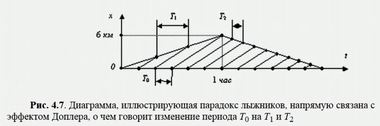
Парадокс лыжников

Поэтому закроем тему парадокса штриха и вернемся к традиционным выражениям, которые работают на ниве акустики, то есть без релятивистских прибомбасов в виде известного корня квадратного из 1 – β². Наша ближайшая задача состоит в том, чтобы понять, откуда в формулах для классической физики взялись косинусы.

Часто, выучив определения каких-то физических понятий, зазубрив правила и законы, мы думаем, что понимаем природу физического явления, но это обманчивое впечатление. Без четких пространственно-механических представлений физику явления понять трудно, если вообще возможно. Ярким подтверждением этого служит нынешнее достаточно уродливое представление об эффекте Доплера.

Традиционная формула (1)

Итак, для звуковых колебаний изменившаяся длина волны в случае движения только источника колебаний описывается традиционной формулой (1). Все величины в ней прежние. Нам так же хорошо известна школьная формула Маха. Если v > c или β > 1, то справедливо выражение 2: sin θ = 1/β = c/v (2)

Формула Маха

Формулы 1 и 2 никак не связаны, хотя с точки зрения непрерывности процесса распространения волн, а именно, монотонного увеличения скорости движения источника, выражение 2 является прямым следствием выражения 1. Однако никакой связи между этими двумя выражениями не видно. Странно это.

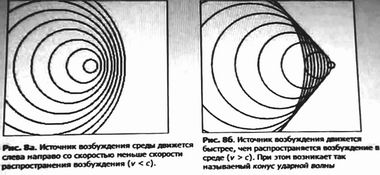
Распространение волн, когда v < c и v > c

Взгляните еще раз на эту анимацию, которая уже демонстрировалась нами. В левом окошке источник возбуждения среды движется слева направо со скоростью меньше скорости распространения возбуждения, т.е. когда v < c. В правом окошке источник возбуждения движется быстрее, чем распространяются возбуждения в среде, т.е. когда v > c. Какова длина волны по линии движения источника мы хорошо знаем: впереди источника длина волны короче λ' = λ(1 – β); позади — длина волны увеличена и равна λ' = λ(1 + β). Вопрос, при каком угле θ можно будет наблюдать равенство λ' = λ?

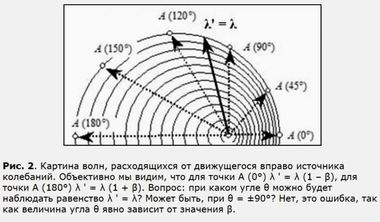
Картина волн, расходящихся от движущегося
вправо источника при v < c

Традиционная формула 1 утверждает, что при прямом угле π/2 косинус равен единице и тогда принимаемая длина волны равна собственной длине волны источника (λ' = λ). Причем этот результат, согласно формуле 1, не зависит от величины скорости источника, т.е. от величины β. Но из чертежа мы прекрасно видите, что это не так. Вектор, соответствующий равенству λ' = λ будет отклоняться влево, т.е. он зависит от величины β.

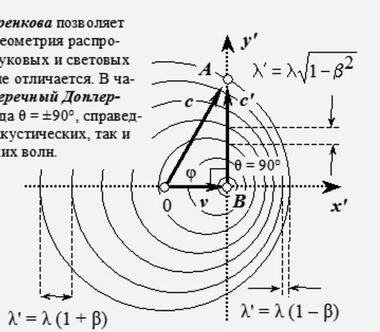
При угле π/2 условие λ' = λ не выполняется

А самое главное, при угле π/2 условие λ' = λ не выполняется. Формула 1 какая-то странная: она не описывает волновую картину, изображенную на рис 2. Более того, воспользовавшись теоремой Пифагора для треугольника АВ0, мы с удивлением обнаруживаете, что длина волны по стороне катета АВ в точности дает так называемый поперечный Доплер-эффект.

Длина волны по стороне катета АВ
дает поперечный Доплер-эффект

Как же так получилось, ведь поперечный эффект имеет место в теории относительности. Мы же находимся в области классической физики. Так, в нас зреет сомнение в отношении справедливости формулы 1. Возникает желание получить формулу для принятой длины волны непосредственно из геометрического рисунка. Это сделать несложно.

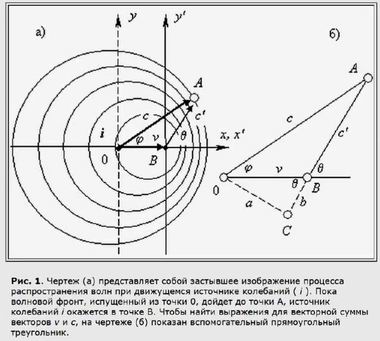
Чертеж для вывода формулы λ'

Вычерчиваем не прямоугольный треугольник, как до этого, а треугольник для произвольного угла φ. Достраиваем его до прямоугольного, пририсовав к нему вспомогательные отрезки а и б. Непосредственно из построения записываем величину отрезков а и б через скорость v (ей отвечает отрезок 0В): a = vsin θ и b = vcos θ.

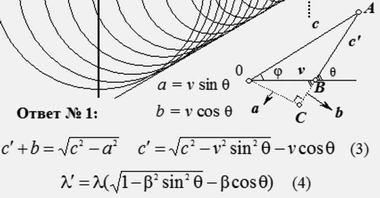
Вывод правильной формулы для λ'

По теореме Пифагора составляем равенство: ... Если в последнее выражение подставить значения a и b, получим искомую скорость c' (3). Умножая обе части равенства (3) на период колебаний Т, получаем изменившуюся за счет эффекта Доплера длину волны λ', которую удобно выразить через параметр β (4).

Теперь формула Маха (2) естественным образом вытекает из формулы (4). При этом формула (4) работает не при всех значениях угла θ. Если подкоренное выражение окажется отрицательным, то корни из него будут мнимыми. Мнимые величины не имеют физического смысла, поэтому на подкоренное выражение накладывается условие:

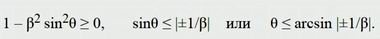
Условие для выполнения формулы (4)

Таким образом, формула Маха (2): sin θ = 1/β = c/v дает возможный угловой сектор распространения волны. Волновой фронт не может выйти за границы сектора, которые совпадают с линиями ударной волной (или конусом ударной волны для пространства трех измерений).

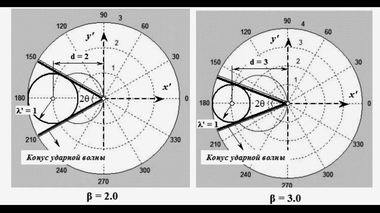
Сектор ударной волны

Вид формулу (4) можно изменить, выразив ее не через угол θ тетте, а через угол фи (оба они показаны на чертеже 2). Тогда формула (4) преобретет вид формулы (5). Можно поступить иначе, если воспользоваться рис. 4.3.

Чертеж 2 для получения формулы (5)

Если вместо теоремы косинусов воспользоваться теоремой синусов, которая дает равенство: sin(θ – φ) = βsinθ, а затем эти синусы выразить через косинусы, то можно получить еще одно математическое выражение (6), в котором будут фигурировать уже как угол наблюдения (θ), так и угол между скоростями v и c (φ):

λ' = λ[cos(θ – φ) – βcosθ]         (6)

Для получения формул 4, 5 или 6 никакого наблюдателя или приемника не требуется. Система концентрических колец со смещенными центрами образуется и без него.

Для получения формул 4, 5 или 6 никакого наблюдателя не требуется

Главное, что здесь нужно, это выразить произвольно взятую окружность корректным образом. Неточная, а правильнее сказать, абсолютно ошибочная формула (1), как мы увидим ниже, является уравнением кардиоиды в полярной системе координат, а полученное нами выражение (4) является уравнением именно окружности, которая фигурирует не только в Доплер-эффекте, но и при интерференции волн на воде или волн в эфире. Угол θ можно сделать свободным параметром, т.е. аргументом воспринимаемой приемником длины волны λ' или сторона АВ, изображенного на рис. 1а треугольника.

Из рис. 1а можно записать три понятных равенства

0А = λ,   0В = βλ   и   АВ = λ'.

В декартовой системе координат (x', y') с началом в центре В, уравнение окружности выглядит следующим образом:

(x' + βλ)² + (y')² = λ².

Произведем переход от декартовых координат к полярным по формулам:

(λ')² = (x')² + (y')²,     x' = λ'cosθ,       y' = λ'sinθ.

Тогда наше уравнение окружности будет иметь вид:

(λ')² + 2βλλ'cosθ – λ²(1 – β²) = 0.

Перед нами обыкновенное квадратное уравнение, решая которое относительно неизвестной λ', мы получаем формулу (4). Окружность получается и в том случае, если для функции λ' выражения (4) построить графики зависимости от аргумента θ, меняющийся в пределах от 0 до 2π. Графики этой зависимости (рис. 3) для β = 3/4 (а) и β = 1 (б) лишний раз подтверждает, что мы имеем дело действительно с окружностями, которые можно видеть, например, на поверхности озера, когда по ней бежит водомер.

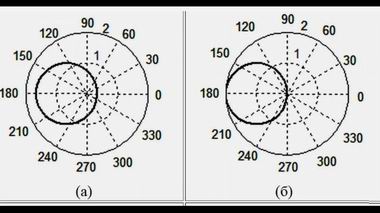
Рис. 3 для уравнения окружности (4) при β = 3/4 (а) и β = 1 (б)

Между тем, традиционное выражение (1), приводимое во всех сегодняшних справочниках и учебниках, окружности не дает. При тех же значениях β волновой фронт как функция λ' от аргумента θ порождает кривые (в и г), которые в математике называются кардиоидами.

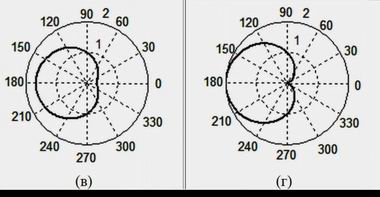
Рис. 3 для уравнения кардиоиды (1) при β = 3/4 (в) и β = 1 (г)

Далее приводятся графики вместе с простенькой программой. Преподаватель может провести практическое занятие на тему "Эффект Доплера", выраженный через старую, неправильную формулу и новую правильную. Старшеклассник или студент-первокурсник, меняя в программе исходные выражения и величину относительной скорости β (в программе параметр b) должен построить графики окружности и кардиоиды. Учащийся должен объяснить полученные графики, проанализировать ошибочность традиционной формулы и правильность новой.

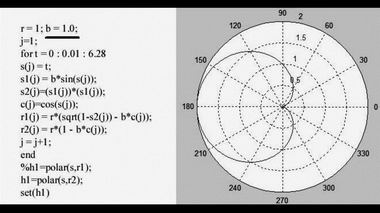
Практическое занятие по теме "Эффект Доплера"

В чём состоит ошибочность традиционных двух обобщенных формул для длины волны и частоты?

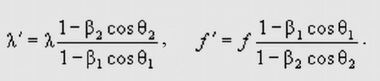
В чём состоит ошибочность этих традиционных формул?

Дело в том, что они имеют дело не суммой двух векторов, а с их проекциями. Автор этих формул (он историкам науки не известен), очевидно, посчитал, если к относительным скоростям β₁ и β₂ приписать по соответствующему косинусу cosθ₁ и cosθ₂, то тем самым будет учтена всевозможная направленность векторов v₁ и v₂, Он думал, наверное, что на изменение длины волны λ' и частоты колебаний f' может оказывать влияние лишь проекции скоростей v₁ и v₂ на вектор c, т.е. величины v_пр1 и v_пр2 (рис. 5), а не сами векторные разности: c – v₁ и c – v₂. Вот в чём здесь ошибка.

Рис. 5

Сейчас проверим, как в новой формуле обстоят дела с явлением, которое релятивисты называют замедлением времени или укорочением собственной длины. Для этого нам нужно определить, как меняется угол θ в зависимости от скорости движения источника β, когда выполняется равенство: λ' = λ. Если подставить данное условие в нашу формулу, то найдется простая зависимость :

β = – 2 cos θ     или     θ = arccos ( – β / 2 ) .

Для наглядности составим таблицу. Из неё видно, что любая скорость источника приводит к отклонению луча, для которого λ' = λ, от вертикальной линии в противоположную сторону от направления движения источника. Как это явление называется в оптике? Оно называется аберрацией, с которой ошибся Майкельсон (эту ошибку мы подробно разбирали в самой первой лекции, т.е. части 1 нашего видеофильма). Если источник покоится, т.е. β = 0, то равенство λ' = λ выполняется при угле θ = 90°.

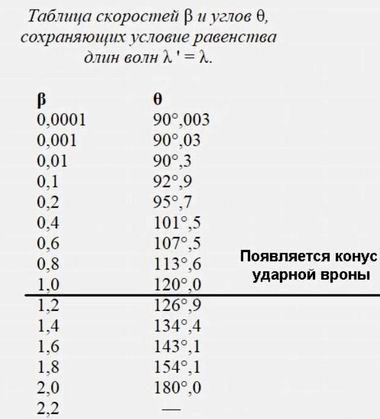
Таблица для выполнения условия λ' = λ

Еще раз повторим: это произойдет в одном-единственном случае, когда никакого Доплер-эффекта нет. Он начинает давать о себе знать, источник начинает двигаться (т.е. β > 0). Тут же начинает проявляться аберрация: луч света с длиной волны λ' = λ отклоняется в противоположную сторону относительно направления движения источника колебаний. Когда β = 1, т.е. скорость движения источника становится равной скорости распространения волн, наступает качественно новая ситуация: появляется конус ударной волны. При этом луч с длиной волны λ' = λ отклоняется на угол в 120 градусов.

Ничто не мешает нам продолжить увеличение источника волн, когда β > 1. Кажется ничего не происходит до значение β = 2 В последнем случае угол становится равным θ = 180°. Что здесь может помешать выполнению условия λ' = λ ? Разве кто-нибудь отменял выше написанные формулы

при θ = 0° ,     λ' = λ (1 – β) ;

при θ = 180° ,     λ' = λ (1 + β).

Да, первая формула для угла θ = 0° здесь отменяется в силу ранее указанных нами ограничений:

1 – β² sin ² θ ≥ 0,     sin θ ≤ ±1 / β     или     θ ≤ ± arcsin ( 1 / β ).

Скорость источника волн может быть любой, ограничений здесь никаких нет. Пусть β = 2,2 , тогда, согласно последнему ограничению, имеем:

θ ≤ ± arcsin ( 0,45 ) = ± 27°.

Это означает, что при β = 2,2 волны не выходят за пределы конуса ударной волны с углами при вершине ±153°, если отсчет вести от положительного направления оси x. Таким образом, при θ = 180° будем иметь λ' = 3,2 λ, что допустимо, а угол θ = 0° в этой ситуации мы просто не имеем права рассматривать. В этом направлении у нас получилась бы отрицательная длина волны λ' = –1,2 λ, что с точки зрения физики лишено всякого смысла.

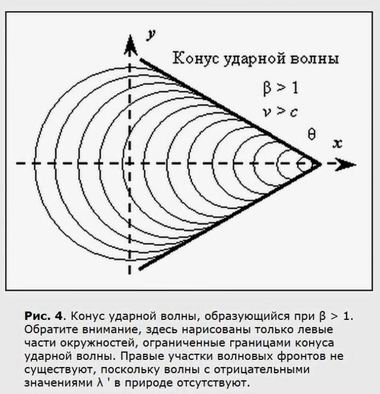
Более того, второе ограничение опережает первое. При любом значении β > 1, когда должны появляться волны с отрицательной длинной,

λ ' = λ (1 – β) < 0,

тут же исчезают правые участки волновых фронтов, распространяющиеся по ходу движения источника колебаний. Вся их колебательная энергия сосредоточивается на границе конуса, что проявляется в виде высокого энергетического барьера.

Рис. 5. Фотография реактивного самолета FA-18, летящего быстрее звука. Вблизи летального аппарата виден светлый конус ударной волн. Дело в том, что сразу же за конусом создается зона пониженного давления, в которой происходит мгновенная конденсация паров влаги. В 1911 году Э. Мах установил, что угол θ при вершине конуса ударной волны всецело определяется относительной скоростью β, поэтому параметр β часто называют числом Маха.

Когда реактивный самолет преодолевает этот мощный звуковой барьер (рис. 5), мы слышим оглушительный хлопок. Если бы реально существовали правые участки всех волновых фронтов, то было бы не понятно, откуда конус ударной волны черпает свою колоссальную энергию, т.е. здесь нарушался бы элементарный энергетический баланс. Кроме того, при сохранении правых участков волновых фронтов внутри конуса образовывалась бы интерференционная картина, (рис. 6) которая в действительности не наблюдается.

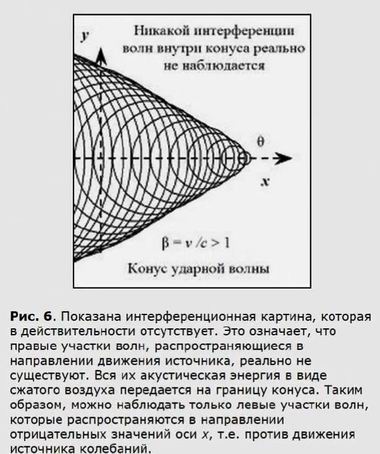
Интерференции внутри конеса не возникает

Все эти нюансы очень важны для осмысления простого математического факта, а именно: традиционная формула, описывающая плоские волны от движущегося точечного источника колебаний в большинстве случаев не работает даже приближенно, т.е.

λ' ≠ λ (1 – β cos θ).

Это ложное для сферических волн выражение не описывает всех тех явлений, о которых только что рассказывалось. То есть, традиционная формула не дает наблюдаемые эффекты, отображенные на рис. 2 – 5. Она не отвечает на два важнейших вопроса: 1) откуда берется конус ударной волны; 2) как истолковать отрицательные длины волн λ ' < 0, когда скорость источника превышает скорость звука β > 1. Но все эти факты получают логическое объяснение, если воспользоваться чуть более сложным выражением, справедливым для любых значений β:

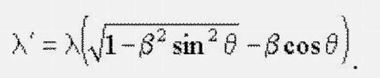
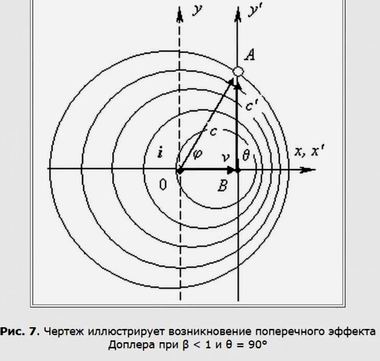
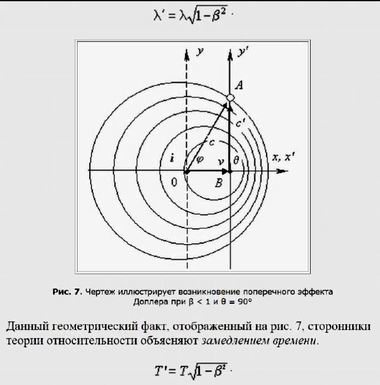
Правильная формула для движущегося источника сферических волн

Если сюда подставить θ = 90°, мы получим выражение, которое в теории относительности получило название поперечного эффекта Доплера. Его суть сводится к уменьшению исходной длины волны λ, генерируемой источником колебаний, до величины λ' (рис. 7):

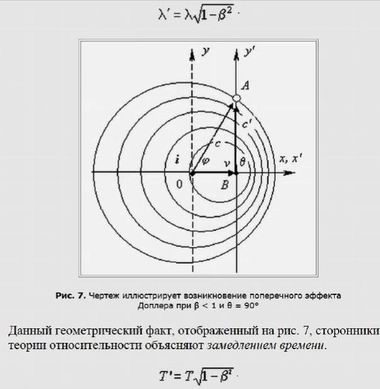
Выражение для поперечного эффекта Доплера

Данный геометрический факт, отображенный на рис. 7, сторонники теории относительности объясняют замедлением времени. Они утверждают, что при θ = 90° выполняется равенство λ' = λ , но за счет «замедления времени» происходит «сокращение длины», так как

λ = cT     и     λ' = cT'.

Для акустики такая логика не приемлема, так как скорость звука и скорость его источников не попадает в релятивистскую область. С самого начала нужно было отказаться от традиционной формулы и использовать формулу Доплера для сферических волн. Однако жесткие философско-методологические ограничения, господствовавшие в науке XX столетия, не позволили этого сделать. Всё, что грозило подорвать теоретическую базу релятивизма, немедленно изгонялось из сферы науки. Сегодня физическая наука переживает глубокий кризис. Можно надеяться, что с его окончанием физики откажутся от формально-спекулятивной идеологии и снова возьмут на вооружение рационально-конструктивную методологию.

Текст статьи 1987 года

В статье 1987 года (ее название и текст вы сейчас видите), по сути, экспериментально доказывается существование поперечного эффекта Доплера для акустического диапазона. Чтобы уловить главную идею статьи, достаточно прочитать аннотацию к ней, в ней говорится:

«Принято считать, что поперечный эффект Доплера первого порядка по v/c (по отношению к β) не существует для всех волновых явлений, включая акустические, т.е. эффект Доплера равен нулю для излучения, направленного перпендикулярно к движению [потока частиц]. Однако такое утверждение предполагает, что падающее поле [ультразвука] представляет собой плоскую волну, что, вообще говоря, не верно для источников с конечной апертурой. Поэтому исследование потоков, перпендикулярных к лучам [ультразвука] конечного диаметра, особенно, когда эти лучи сфокусированы, вполне возможно. Подобная геометрия будет полезна в тех случаях, когда не возможна традиционная ориентация ультразвукового луча вдоль направления потока. Исходя из этих соображений, здесь представлены теоретически и экспериментально выполненные измерения доплеровского спектра для поперечных конфигураций.

Сравнение измерений текущего потока с измерениями, полученными на основе стандартной ультразвуковой Доплер-системы, показывает, что скорость потока, перпендикулярного к оси сфокусированного датчика может быть измерена с точностью, которая сопоставима с точностью, полученной при помощи традиционной системы с наклонной ориентацией [ультразвукового луча]. Измерение Доплер-спектра показывает высокую степень согласованности с теорией.

Хотя эксперименты были проведены для акустических волн, представленные результаты должны быть применимыми также и к электромагнитным системам».

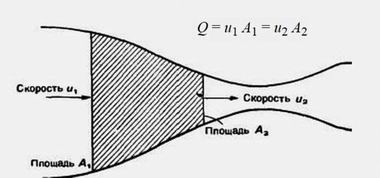
Cужение просвета в сосуде приводит к увеличению
скорости потока (в данном случае u2)

Поясним эту аннотацию. Из физики известно, что сужение просвета в сосуде приводит к увеличению скорости потока. Следовательно, в сосуде, в котором образовались бляшки, кровь будет течь быстрее, чем в других частях этого сосуда. Данное требование вытекает из закона сохранения массы: жидкая масса (вода, кровь, лимфа), вытекающая из системы трубок, должна быть в точности равна массе втекающей жидкости. УЗИ-прибор позволяет найти места, нарушившие кровоснабжение органа или ткани по причине закупорки сосуда какими-либо частицами.

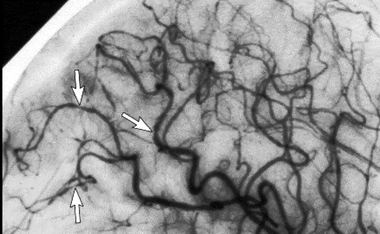
Стрелками указаны места сужения сосудов

Пускай через клапан аорты сердечной мышцы кровь выталкивается со скоростью v = 2 м/с. Если смотреть на вектор скорости под углом θ = 0°, то cos θ = 1 и воспринимаемая датчиком скорость будет в точности равна: v' = v = 2 м/с. Если смотреть на вектор под углом θ = 90°, то cos θ = 0 и воспринимаемая датчиком скорость v' = 0 м/с. Если взять три значения угла, например, θ = 10°, 30° и 60°, то воспринимаемая датчиком скорость v' = v cos θ будет соответственно равна v' = 1.97 м/с, 1.73 м/с и 1.0 м/с (на рис. 4 все это видно).

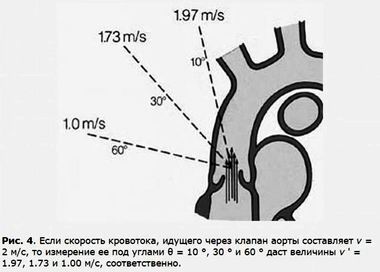
Клапан аорты сердечной мышцы

Поскольку локация эритроцитов производится при помощи ультразвука, распространяющегося со скоростью с = 1540 м/с, то воспринимаемая датчиком скорость будет не v', а

с' = с – v cos θ,

которая и определяет закон Доплера в его традиционном понимании.

В УЗИ-аппарате используется принцип локации, поэтому обобщенная формула для частоты упрощается,

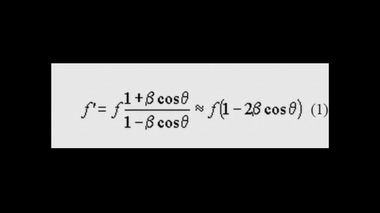
Формула (1)

так как принимаются равенства

θ1 = θ2 = θ , β = β2 = – β1.

Отсюда находится относительная скорость β. Эти выражения удовлетворительно работают на острых углах θ, где-то до значения θ = 60 градусам. Нас же сейчас интересует угол θ = 90 градусов. Обобщенная новая наша формула имеет вид (2). Для нее относительная скорость β определяется формулой (2а), а когда имеем угол 90 градусов, выражение (2а) сводится к формуле (2b).

Обобщенная новая формула (2)

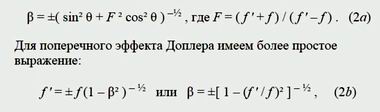
Выражение (2а) сводится к формуле (2b)

Графике (рис 10) наглядно демонстрирует успешность нахождения различных значений скорости кровотока, когда ультразвуковое излучение направлено перпендикулярно к направлению скорости кровотока (когда θ = 90°). Для сравнения на этом же графике (рис 10) приведены значения скорости для угла θ = 60°, когда используется традиционное приближение (1b) (о формулах 2, 2a и 2b авторы статьи, по-видимому, ничего не знали).

Итак, зная объемный расход жидкости и площадь сечения трубки, можно вычислить осевую скорость кровотока v1 (по центре сосуда кровь течет равномерно и максимально быстро). Эксперимент проводился для пяти значений таких скоростей:

v1-1 = 43 см/с,
v1-2 = 60 см/с,
v1-3 = 74 см/с,
v1-4 = 93 см/с,
v1-5 = 121 см/с.

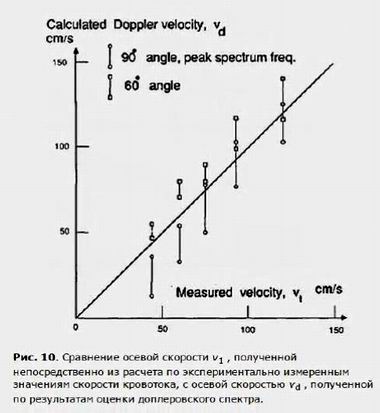
График (рис. 10)

Осевая скорость кровотока vd , рассчитанная по доплеровским спектрам, находится в доверительных интервалах (они отмечены на графике рис 10):

vd-1 60° = 23 ± 12 см/с,   vd-1 90° = 50 ± 4 см/с,
vd-2 60° = 41 ± 10 см/с,   vd-2 90° = 72 ± 5 см/с,
vd-3 60° = 62 ± 13 см/с,   vd-3 90° = 81 ± 5 см/с,
vd-4 60° = 86 ± 10 см/с,   vd-4 90° = 106 ± 7 см/с,
vd-5 60° = 110 ± 11 см/с;   vd-5 90° = 126 ± 12 см/с.

Для угла θ = 60° оценка доплеровской скорости vd рассчитывалась, исходя из «стандартного уравнения Доплера» :

fd = 2f0 (v/c) cos θ ,

где f0 — собственная частота излучателя, fd — доплеровская частота и θ — угол между осью луча и направлением скорости кровотока.

Для угла θ = 90° оценка по всем пяти скоростям v1 производилась по максимуму спектральной амплитуды треугольного спектра, который показан на рис. 11.

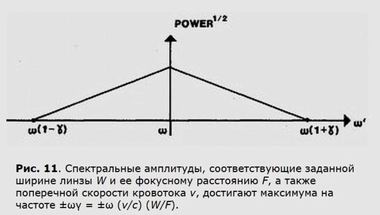
График (рис. 11)

Возможно, что на практике строго детерминистская формула (2) еще долго не будет играть определяющую роли, так как ее точность не достижима для статистической измерительной системы с ограниченной фокусировкой луча и конечной апертурой датчика. Выражение ( 2b ) дает математически безукоризненную взаимосвязь между скоростью β и частотным сдвигом Δ f при θ = 90° — другой формулы просто не существует.

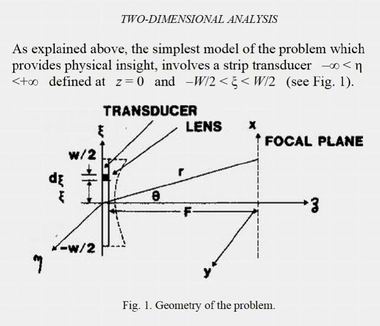
Анализ задачи в случае двумерной геометрии

Главным же в ультразвуковой диагностике оказывается регистрация факта существования поперечного эффекта Доплера, который возникает не в результате эфемерного замедления времени, как учат нас релятивисты, а за счет искривления волнового фронта или, иначе сказать, отсутствия условий для существования идеальных плоских волн, для которых используется традиционная формула (1).

Замедление времени не существует

То, что эффект Доплера в оптическом диапазоне ничем не отличается от эффекта Доплера в акустическом диапазоне, известно давно. В 1934 аспирант Сергея Вавилова, Павел Черенков, при изучении люминесценции зарегистрировал свечение, исходившее от электронов, летящих в прозрачной среде. Этот факт получил название эффекта Вавилова – Черенкова. Примерно через два года ими была получена формулу (3):

cos φ = 1/nβ,             φ = arccos (1/nβ),       (3)

где n — показатель преломление среды.

Эффект Вавилова – Черенкова

Как рассказывал Черенков, наибольшей экспериментальной трудностью оказалось обнаружение направленности излечения: ударная волна распространяется по направлению движения частиц под углом ±φ. После получения фотографий черенковского излучения (рис. 5а) и построения кривых его интенсивности (рис. 5б) написание формулы (3) уже не представляло большой проблемы.

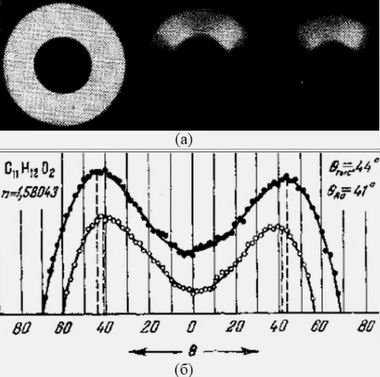
Рис. 5

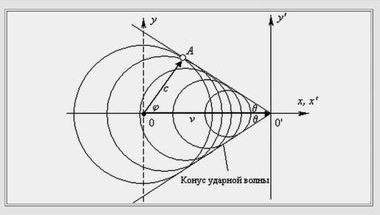
Рис. 4

Рис. 4 показывает, что выражение (3) является просто-напросто другой тригонометрической формой выражения Маха.

Таким образом, Черенков наткнулся на оптическое явление, которое говорило об идентичной природе электромагнитных и акустических волн. Однако его руководитель Сергей Вавилов, вместе с Иоффе, Таммом и другими релятивистами в 30-х годах возглавлял группировку академиков, боровшихся с представителями старой советской школы классической физики (Кастериным, Тимерязевым, Миткевичем, Цейтлиным и другими). Таким образом, эффект Черенкова до сих пор стоит в стороне от столбовой дороги, проложенной Доплером еще в середине 19-го века.

Мировоззрение релятивиста радикальным образом отличается от мировоззрения рационалиста-конструктивиста. Последний живет на земле, первый — на небе, вечно витает где-то в облаках, выдвигает самые нелепые идеи. Мы уже говорили в начале этой лекции, повторим еще раз: теории античных софистов и средневековых схоластов не идут ни в какое сравнение с мифами нынешних релятивистов. Быстро пролетит время, и историки науки начнут недоумевать: как они могли после Фарадея возвысить до небес Эйнштейна? Мы, историки науки, летописцы человеческой глупости, тоже можем спросить: а как после Архимеда можно было молиться на Аристотеля? В Средние века наука явно покатилась вспять. Больше того, в средневековых университетах всерьез заговорили об ангелах, преисподней и прочих благоглупостях. Человек не меняется. В сегодняшних университетах снова заговорили о пришельцах из потустороннего мира и параллельных мирах.

Об этом не перестают говорить и релятивисты. Им всё сходит с рук, они просто завидные визунчики. В самом деле, мы рассказывали, насколько не похожи формулы, которыми оперирую рационалисты и релятивисты. Эти формулы получились из совершенно противоположных мироощущений, однако числовые результаты из этих формул почти идентичны.

Математикам известны три следующих приближения.

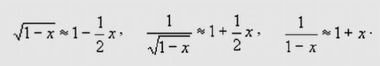
Они вполне удовлетворительно выполняются, если х достаточно мало, т.е. много меньше единицы. Если же х подбирается к единице, а тем более становится больше единицы, то эти приближения становятся слишком грубыми, т.е. вовсе уже и никакие не приближения.

Применим их к нашим новым формулам для движущегося источника и покоящегося приемника

            (1)

для движущегося наблюдателя и покоящегося источника:

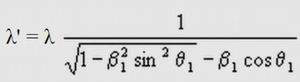
и для совместного движения источника и приемника, если источник и наблюдатель движутся одновременно:

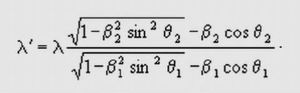
Давайте проверим, как всё это работает на практике. С этой целью напишем простенькую программку, и последовательно будем менять в ней исходное уравнение и параметр β.

r = 1; b = 3/4; j=1;
for t = 0 : 0.01 : 6.28
s(j) = t; s1(j) = b*sin(s(j));
s2(j) = (s1(j))*(s1(j));
c(j) = cos(s(j));
% точная формула (1):
r1(j) = r*(sqrt(1 - s2(j)) - b*c(j));
% традиционная формула (2):
r2(j) = r*(1 - b*c(j));
% релятивистская формула (8):
r8(j) = r*sqrt(1 - b*b)/(1 - b*c(j)); % релятивистская формула (9):
r9(j) = r*(1 - b*c(j))/sqrt(1 - b*b);
% релятивистская формула (10):
r10(j) = r*sqrt(1 - b*b)/(1 + b*c(j));
j = j + 1;
end
h1 = polar(s,r1);
%h1 = polar(s,r2);
%h1 = polar(s,r8);
%h1 = polar(s,r9);
%h1 = polar(s,r10);
set(h1);

Сначала возьмем формулу (1). На рис. 3 приведены результаты работы программы для формулы (1) при значении β = 3/4, на рис. 4 – при β = 1.

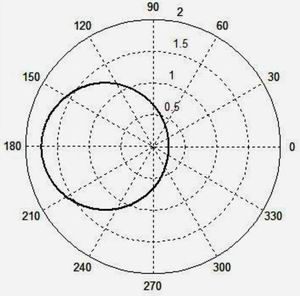
Рис. 3

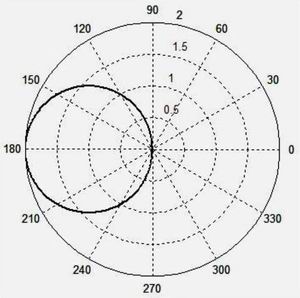
Рис. 4

Затем возьмем традиционное равенство (2) для движущегося источника.

            (2)

Выражение (2) дает кардиоиды; на рис. 5 при β = 3/4 и рис. 6 при β = 1.

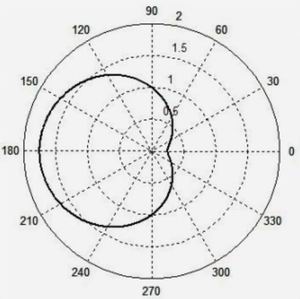
Рис. 5

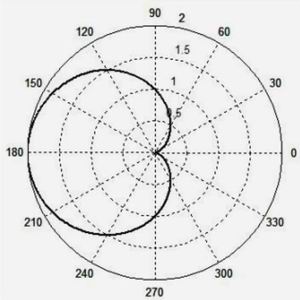
Рис. 6

Наконец, в нашу программу подставляем релятивистскую формулу (3)

            (3)

На рис. 7 показана диаграмма зависимости λ' от угла θ, рассчитанная по формуле (3) при λ = 1 и β = 3/4, а на рис. 8 – при β = 0,99 (при β > 1 формула (3) перестает работать).

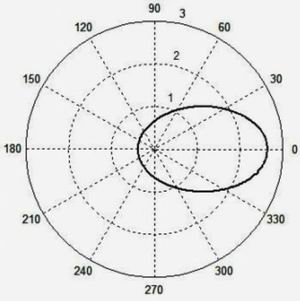
Рис. 7

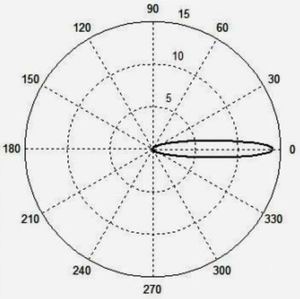
Рис. 8

Волновой фронт, рассчитанный по формуле (3), представляет собой эллипс, что противоречит основополагающему принципу Гюйгенса. Обратите внимание, при β = 3/4 большая ось эллипса вытянулась до 2.7, а при β = 0,99 эллипс растягивается до величины 14 единиц. Таким образом, релятивистская формула (3) явно ошибочна.

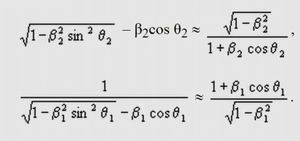
Итак, когда β мало, релятивистские формулы мало, чем отличаются от наших классических для сферически распространяющихся волн. Поэтому мы и говорим, что релятивистам в этом конкретном месте необычайно повезло.

В методе Доплера, который используется для поиска экзопланет значение β невелико, так как экзопланеты не слишком-то быстро колеблют возле звезды. Перемещение спектральных линий происходит медленно, поэтому используемая релятивистами методика, о которой шла речь в начале нашей лекции, вполне пригодна.

Экзопланеты не слишком быстро колеблют возле звезды,
поэтому перемещение спектральных линий происходит медленно

Трудно сказать, почему метод Доплера сегодня проигрывает перед транзитным — детали расчетов нам не известны — но вряд ли это произошло по причине множественности экзопланет, вращающихся вокруг одной звезды. Что здесь имеется в виду?

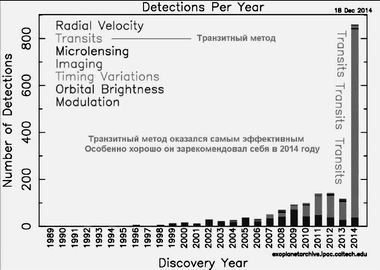
Трудно сказать, почему метод Доплера сегодня проигрывает перед транзитным

Известно, что центр масс Солнечной системы описывает сложную траекторию в течение длительного времени. Кажется, что по конфигурации этой траектории ничего не возможно сказать об орбитах экзопланет и их параметрах. Тем не менее, эта задача не выглядит неразрешимой. При сегодняшнем уровне вариационных программ можно отыскать несколько приемлемых вариантов. В поиске подгоночных коэффициентов могут использоваться результаты, полученные другими методами, в частности, транзитным методом.

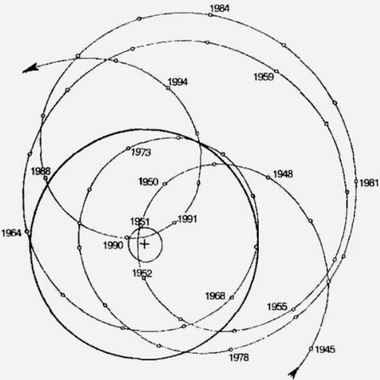
Центр масс Солнечной системы описывает сложную
траекторию в течение длительного времени

Релятивистам также страшно повезло с методом гравитационного микролинзирования. Метод основывается на факте искривления лучей света вблизи массивных тел. Данный факт был предсказан общей теорией относительности, и якобы успешно подтвержден в 1919 году. Не станем сейчас разбирать саму методику поиска экзопланет с помощью гравитационной линзы; скажем несколько слов о степени правдивости указанного релятивистами факта искривления лучей света во время затмения 1919 года, а также других последующих затмений, произошедших в 1921 году и в 1922 году.

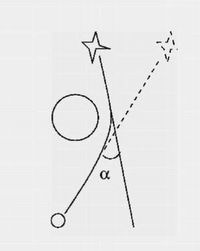
Согласно ОТО, луч света звезды вблизи Солнца
изменит свой прямолинейный путь

Итак, согласно ОТО, луч света звезды вблизи Солнца изменит свой прямолинейный путь; степень искривления характеризуется углом "альфа". Взгляните на этот рисунок, нарисованный после затмения 1922 года. На нём черными точками показаны более трех десятков звезд, у которых имеются хвостики. Эти хвостики показывают величину отклонения положения звезды во время затмения.

Положение звезд при затмении 1922 года

Наше возражение состоит в следующем. Если бы здесь возникла гравитационная линза, как утверждают релятивисты, то все хвостики, т.е. видимые отклонения звезд, лежали бы на радиальных линиям, которые сходились бы в центре Солнца. Гравитационное поле Солнца сферическое, т.е. строго симметричное. Здесь же мы видим, что звезды отклонились абы как, случайным образом. Причем, находясь примерно на одном расстоянии от Солнца, они почему-то отлетели на различные расстояния. Почему длина звездных хвостиков столь различна?

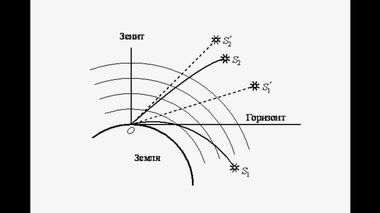
Атмосферная рефракция, в результате чего происходит
преломление световых лучей от небесных светил

И, наконец, самое главное возражение. Каждый школьник слышал об атмосферной рефракции, в результате чего происходит преломление световых лучей от небесных светил. Атмосфера Солнца распространяется на многие миллионы километров. Меркурий и частично Венера находятся в плотном газовом облаке, которое постоянно испытывает флуктуации в результате неровной деятельности светила. Так, может быть, случайные отклонения звезд появились в силу этих случайных флуктуаций атмосферы Солнца?

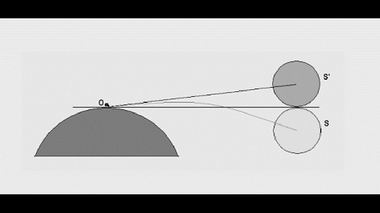
Солнечная атмосфера существует, и она должна вызывать
рефракцию лучей, приводящую к сдвигу видимых положений звезд

Как бы там ни было, солнечная атмосфера существует, и она должна вызывать рефракцию лучей, приводящую к сдвигу видимых положений звезд, т.е. действовать, как своеобразная линза. Честный релятивист должен задать себе вопрос, какая доля отклонения лучей от звезд обусловлена плотной атмосферой Солнца, а какая доля приходится на искривление лучей света в гравитационном поле Солнца. Увы, подобными вопросами релятивисты не мучают себя.

См. фильм с этим текстом

http://youtu.be/x20e0R7y2es