О.Е. Акимов

Конструктивное познание (Часть 18)
Уравнения квантовой физики

Так выглядит формула кинетической энергии в классической механике:

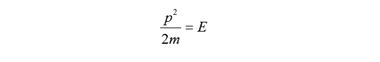
Если имеем дело с электроном, то m – его масса, p – импульс и E –энергия. В квантовой механике энергия и импульс заменяются операторами:

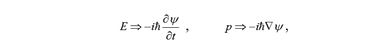
здесь ħ = h/2π – постоянная Планка, i – мнимая единица, ψ – волновая функция электрона, а набла

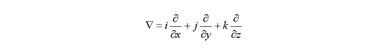
– оператор, с помощью которого удобно выражать операции в векторной алгебре. Мы ими уже пользовались, но не лишним будет напомнить их определение.

Если вектор ∇ скалярно умножить на функцию ψ, то получим вектор

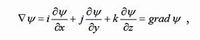
который называется градиентом функции ψ.

Если вектор ∇ скалярно умножить на вектор a, то получим скаляр

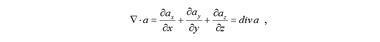
который называется дивергенцией вектора a.

Если вектор ∇ векторно умножить на вектор a, то получим вектор

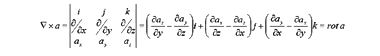
который называется ротором вектора a.

Скаляное произведение оператора набла на оператор набла дает скалярный оператор Лапласа

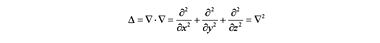
Теперь вернемся к механике. Если выражение для кинетической энергии записать в операторном виде, то получим уравнение Шредингера

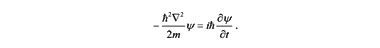
Если вместо классического выражения для кинетической энергии воспользоваться релятивистской формулой

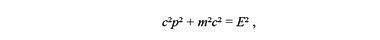
и произвести в ней соответствующую замену на операторы, то мы получим уравнение Клейна — Гордона, описывающее частицы без спина

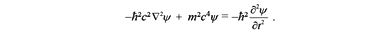
Понизив степень уравнения Клейна — Гордона на порядок, получаем уравнение Дирека для электрона, имеющего спин 1/2

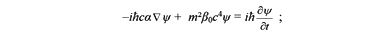
здесь α – 4 × 4 матрицы, составленные из матриц Паули

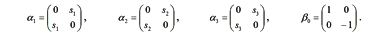
Из трех α-матриц и одной βо конструируют четыре γ-матрицы, которые называются матрицами Дирака

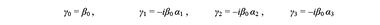
На базе γ-матриц можно простроить 16-компонентную алгебру Клиффорда вида

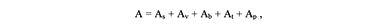
здесь As – скаляр, Av – вектор, Ab – бивектор, At – тривектор, Ap – псевдоскаляр. Базисом этой алгебры выглядит следующим образом

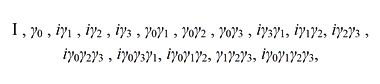
где I – единичная 4 × 4 матрица, i – мнимость.

Запишем уравнение Дирака через γ-матрицы. С этой целью уравнение Дирака, записанное через три α-матрицы и одну βо-матрицу умножим на множитель iħβо, получим уравнение следующего вида

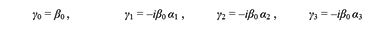
Если воспользоваться оператором 4-импульса, то уравнение Дирака предстанет в более компактной форме

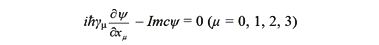
Его решением является плоская волна вида

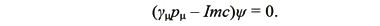
Таким образом, уравнение Дирака представляет собой волновое уравнение. К нему Дирак пришел естественным путем, когда захотел уравнение Шредингера сделать инвариантным для преобразований Лоренца. Ведь можно идти обратным путем, т.е. оттолкнуться от выражения для плоской волны, которая в наиболее общей форме выглядит как

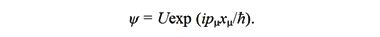
Если функцию ψ один раз продифференцировать по времени

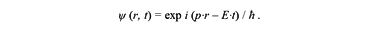
и дважды по координатам

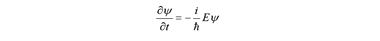
а затем два последних выражения приравнять по Eψ , помня, что

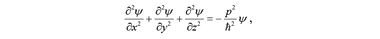
то в результате получаем уравнение Шредингера

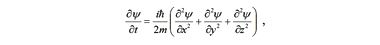
которое удобно записать через оператор набла в квадрате

Среди решений этого уравнения имеются такие, которые зависят только от времени

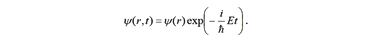
Подставляя это решение в уравнение Шредингера, находим стационарное уравнение для свободного электрона

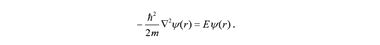
При наличии независимого от времени потенциального поля V(r) последнее уравнение приобретет вид

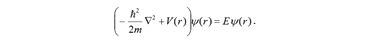
Если вместо кинетической энергии одного-единственного электрона, находящегося в потенциальном электрическом поле, имеется множество электронов, взаимодействующих друг с другом и с остовом кристаллической решетки, то скобка с двумя слагаемыми заменяется гамильтонианом (H). Уравнение Шредингера приобретает вид

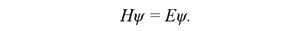
В качестве гамильтониана H при числовом расчете электронных энергетических уровней в кристаллических полупроводниках чаще всего выступает матрица, которая учитывает все энергетические взаимодействия в кристаллической решетке.

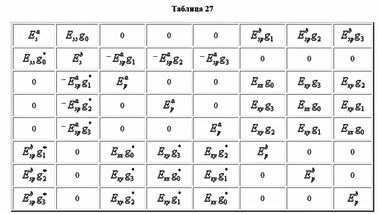
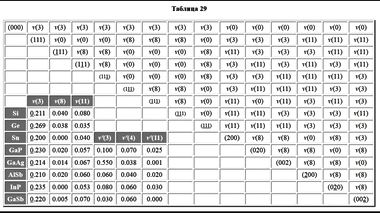
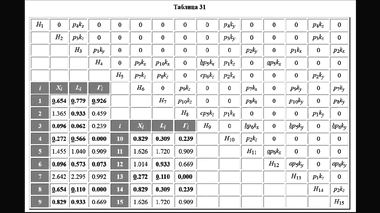
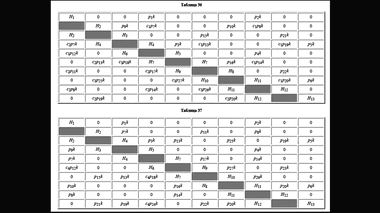
Физика твердого тела начинается тогда, когда теоретик начинает размышлять, как ему сконструировать гамильтониан. Прежде чем погрузиться в толстые слои конденсированного вещества, давайте оглянемся назад и осмотримся по сторонам. Из наших экскурсов в историю физики мы уже знаем, что жизнь науки ничем особенным не отличается от жизни общества. Бывают периоды, когда общество забывает предшествующие события и все достижения текущего момента и готово приписывать какому-нибудь кумиру, который правдами и неправдами оказался на вершине социальной пирамиды. Так было, например, со Сталиным, которому целиком приписали победу во Второй мировой войне, забывая о проявленном героизме бесчисленных анонимов, воевавших на полях сражения. Так было с Ньютоном, который не открывал три закона, носящих сейчас его имя, и закон всемирного тяготения открытый Робертом Гуком.

Релятивисты восхищаются красивой аналогией кривизны пространства, которую якобы впервые предложил Эйнштейн. Но если бы они лучше знали историю физики, то должны были бы упомянуть имя всё того же Гука. В диалогах с Ньютоном, которые в большинстве случаев проходили заочно, Гук для разъяснения эллиптических орбит планет приводил пример не только коническую поверхность, по внутренней поверхности которой катилась планетные тела, но и конический маятник, описывающий эллипсы. По отклонению оси маятника и по измененному периоду колебания он пытался установить степень несферичности Земли.

Сегодня только и говорят о бозоне Хиггса, что можно подумать, будто Питер Хиггс придумал что-то такое, чего до него никто не знал. В действительности, Хиггс высказал старую идею Джозефа-Джона Томсона, которую сначала у этого физика похитил "скромный" Эйнштейн, а позже, придав идее новое словесное обличие, преподнес забывчивой общественности уже в третий раз "первооткрыватель" Хиггс.

В чем заключается идея Томсона?

Еще в 1881 году 25-летний Томсон ввел понятие "связанной с эфиром массы". Движущееся сквозь эфир тело, рассуждал он, должно испытывать сопротивление эфирной среды, которое равносильно увеличению массы тела. Со временем эта мысль приобретала у него более конкретные очертания, особенно, после открытия им в 1897 году электрона (см. Биография Дж. Дж. Томсона. Электрон: история открытия и первые теории).

Сейчас мы покажем несколько любопытных страниц из книги Томсона, написанной по следам прочитанных им лекций в мае 1903 года, т.е. за два года, когда Эйнштейн опубликовал первую работу по теории относительности, и спустя много лет после, зарождения его теории "связанной с эфиром массы". "Нажмите на паузу и прочтите!" (см. Материя и эфир).

Исследуя отклонение катодных лучей в магнитном и электрическом полях, Томсон обнаружил, что лучи представляют собой поток отрицательно заряженных частиц. Проводя бесчисленное количество опытов над ними, измеряя отношение заряда электрона к его массе, он показал, что открытые им частицы почти в 2000 раз легче самого легкого элемента — атома водорода. Самое же главное открытие, которое у него без зазрения совести украли релятивисты, заключается в идее, высказанной им еще в молодости, а именно: масса электронов или β-частиц, из которых состоят катодные лучи, будет расти с увеличением скорости.

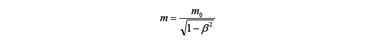
Согласно Томсону, связанная масса электронов в электрическом поле равна кинетической энергии

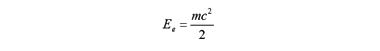
Но ровно такую же энергию электрон приобретет, двигаясь в магнитном поле

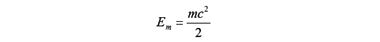
Следовательно, в электромагнитном поле двойка, стоящая в знаменателе формул, исчезнет, поскольку полная энергия движения электрона складывается из этих двух равных друг другу (E_e = E_m) энергий

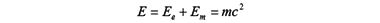
Для Эйнштейна эфир не существовал.

Поэтому увеличение массы электрона во время его движения сквозь пустоту он объяснял кинематическим эффектом, полученным за счет спекулятивных преобразований Лоренца. При этом он извратил идею Томсона, полагая, что энергия электрона сосредоточена в его массе.

Хиггс вернулся к первоначальной идее Томсона путем введения особого поля, которое сегодня называют его именем. Для автора тоже, как будто бы не существовал материальный эфир, но за счет достаточно искусственного деления частиц на фермионы и бозоны он вместе со всеми современными мифотворцами стал говорить о виртуальном пространстве, в котором, дескать, и существует поле Хиггса.

Это эфемерное поле сообщает всем движущимся через него частицам реальную массу. Однако толкователи-популяризаторы заумных фантазий нынешних оракулов от науки по-прежнему оперируются образами, которые в конце 19-го века возникли в голове Томсона.

Они сравнивают частицу с лыжником-слаломистом, стремительно съезжающим с горного склона. Лыже отбрасывают в стороны массу снега, снег оказывает сопротивление движению, стало быть, дополнительную массу лыжника за счет его взаимодействия со снежным покровом можно считать вновь приобретенной.

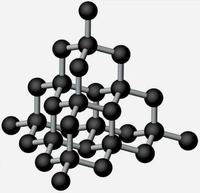
Почему мы вспомнили об этих исторических фактах? Дело в том, что вскоре после смерти Томсона его прозорливая идея о переменной связанной с эфиром массе перекочевала в физику твердого тала. Тут она неизбежно претерпела некоторые изменения, которые, однако, ничуть не изменили ее суть. Физики-твердотельщики тоже не говорили об эфире, но электроны могут двигаться сквозь электрически заряженную решетку. Таким образом, при своем движении через кристаллическое поля они испытывают периодическое воздействие со стороны остова. Это внешнее воздействие со стороны решетки переносят на массу электронов (или дырок, если иметь в виду полупроводники), которую в этом случае называют "эффективной массой" (см. Эффективная масса и поверхность Ферми).

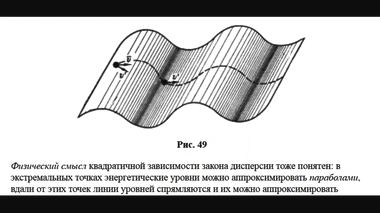
Двигаясь по различным направлениям внутри кристалла, носители положительного и отрицательного электричества будут испытывать различное воздействие со стороны периодического поля. Поэтому эффективная масса носителей выражается тензором.

Как ее можно определить? Ответ: с помощью так называемых зонных структур.

Они представляют собой множество энергетических уровней для возбужденных электронов. Зонные структуры определяют законы дисперсии, т.е. законы рассеяния электронов на кристаллических решетках, если говорить об алмазоподобных полупроводниках.

Смотрите фильм с этим текстом:

http://youtu.be/I4vZd61jAis