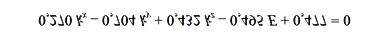О.Е. Акимов

Конструктивное познание (Часть 19)
Энергетические уровни электронов в 3D k-пространстве кристалла.

Почему мы вспомнили об этих исторических фактах? Дело в том, что вскоре после смерти Томсона его прозорливая идея о переменной связанной с эфиром массе перекочевала в физику твердого тала. Тут она неизбежно претерпела некоторые изменения, которые, однако, ничуть не изменили ее суть. Физики-твердотельщики тоже не говорили об эфире, но электроны могут двигаться сквозь электрически заряженную решетку. Таким образом, при своем движении через кристаллическое поля они испытывают периодическое воздействие со стороны остова. Это внешнее воздействие со стороны решетки переносят на массу электронов (или дырок, если иметь в виду полупроводники), которую в этом случае называют "эффективной массой" (см. Эффективная масса и поверхность Ферми).

Двигаясь по различным направлениям внутри кристалла, носители положительного и отрицательного электричества будут испытывать различное воздействие со стороны периодического поля. Поэтому эффективная масса носителей выражается тензором.

Как ее можно определить? Ответ: с помощью так называемых зонных структур.

Они представляют собой множество энергетических уровней для возбужденных электронов. Зонные структуры определяют законы дисперсии, т.е. законы рассеяния электронов на кристаллических решетках, если говорить об алмазоподобных полупроводниках.

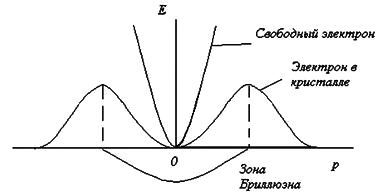
Кинетическая энергия электрона E зависит от волнового вектора k, что и называется законом дисперсии E(k). По квадратичному закону найдем первую и вторую производную функции E(k):

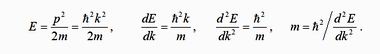
Вспоминаем, что первая производная от какой-либо функции означает скорость изменения функции, вторая производная — степень кривизны функции. Таким образом, масса свободного электрона обратно пропорциональна кривизне функции E(k).

Так как уравнение E(k) представляет собой сферу, поверхность которой имеет постоянную кривизну, то электрон будет иметь неизменную массу, куда бы он ни полетел. Но в кристалле закон дисперсии намного сложнее. Изоэнергетические поверхности отличаются от сферических и, следовательно, масса электрона зависит от направления его движения в k-пространстве:

если         d²E/dk² > 0,     то m > 0;         если         d²E/dk² < 0,     то m < 0.

Отрицательной массой обладают дырки, положительной — электроны. При смене знака вторая производная закона дисперсии должна быть равна нулю: d²E/dk² = 0, что соответствует бесконечно большому значению массы электрона или дырки. Никакая сила не способна перенести частицы с массой m = ± ∞ из одной точки k-пространстве в другую.

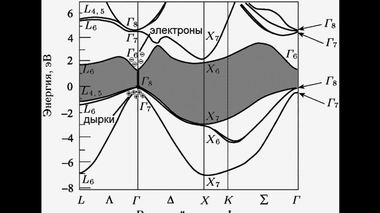
Отсюда следует, что эффективная масса имеет физическое значение вблизи дна зоны проводимости для электронов и вблизи потолка валентной зоны для дырок. Между этими уровнями лежит запрещенная зона. Закон дисперсии вблизи экстремальной точки k₀ n-го энергетического уровня запишется как

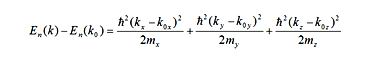
Часто два из трех компонентов эффективной массы одинаковые, и тогда говорят о продольной и поперечной массе.

Физический смысл эффективной массы состоит в том, что направление ускорения электрона (dv/dt) под действием кристаллического поля V(r) не совпадает с направлением силы (F). Если в изотропном пространстве движение электрона описывается вторым законом Ньютона:

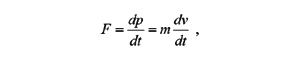
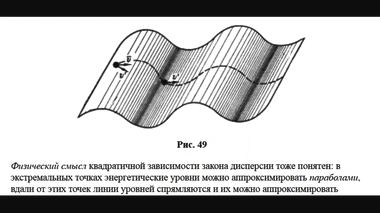
то в анизотропном пространстве кристалла масса в этом школьном законе зависит уже от направления движения (рис. 49). Таким образом, ускорение электрона будет не совпадать с направлением силы:

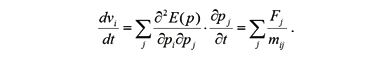
Физический смысл квадратичной зависимости закона дисперсии тоже понятен: в экстремальных точках энергетические уровни можно аппроксимировать параболами, вдали от этих точек линии уровней спрямляются и их можно аппроксимировать прямыми или, если речь идет о k-пространстве, то плоскостями (см. Линейная аппроксимация закона дисперсии).

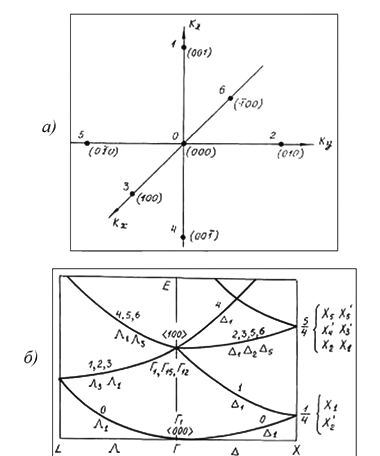
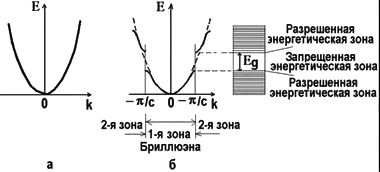
При поиске параметров импульса возникает потребность опереться на какую-то ориентировочную модель всех энергетических уровней. Эту модель не может дать зонная структура пустой решетки (рис. 44а), поскольку вблизи запрещенной зоны кристаллический потенциал слишком сильно искривляет общую картину энергетических состояний (см. рис. 44б). Значит, требуется более адекватная пространственная модель уровней, дающая наглядное представление о расположении энергетических зон.

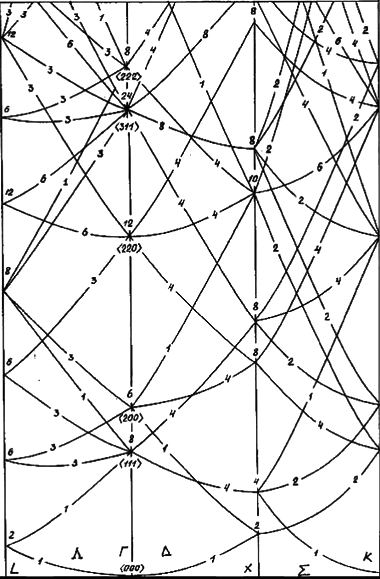
Такая модель может быть получена за счет линейной аппроксимации закона дисперсии, когда ее квадратичный компонент опускается, а линейный удерживается (см. Линейная аппроксимация закона дисперсии):

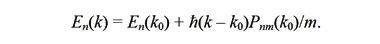
Линейный закон описывает положение плоскостей в четырехмерном пространстве энергии и волнового вектора (E, k_x, k_y, k_z). Таким образом, ставится задача получения числовых значений коэффициентов уравнений плоскости для энергетических уровней, например, германия и кремния. Прежде чем переходить к рассмотрению конкретных законов дисперсии нужно иметь в виду, что существует несколько способов построения гамильтонианов. Среди них выделяется два принципиально различных модели: модель слабой связи и модель сильной связи.

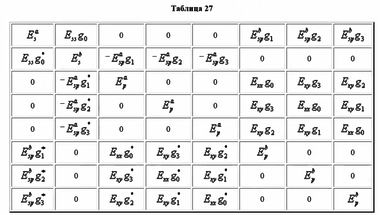
К Модели сильной связи относится так называемый ЛКАО-гамильтониан (ЛКАО расшифровывается как линейная комбинация атомных орбиталей). В этой модели все электроны оказываются связанными с ядрами своих атомов, и только сближение этих атомов внутри кристалла приводит к перекрытию волновых функций электронов, что влечет за собой перестройку орбиталей. Чем ближе атомы в кристалле, тем интенсивнее взаимодействие между электронами, а значит, тем больше значения интегралов перекрытия атомных орбиталей, которые выступают в качестве матричных элементов в матрице ЛКАО-гамильтониана.

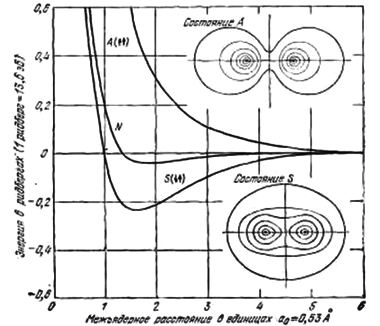
В Модели слабой связи электроны перемещаются внутри кристалла почти свободно. В нулевом приближении потенциал узлов решетки принимается за ноль, электрон абсолютно свободно перемещается внутри остова. Его движение описывается квадратичным законом дисперсии, справедливым для пустого пространства. При потенциале, отличном от нуля, электрон теряет часть свободы перемещения, закон дисперсии становится отличным от квадратичного, но зависимость движения электрона от потенциала решетки выражается все же намного слабее, чем в модели сильной связи.

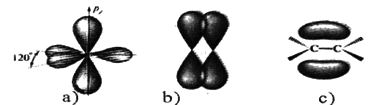
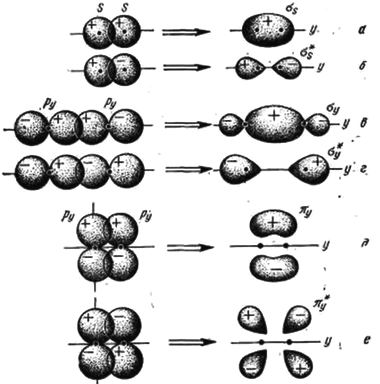
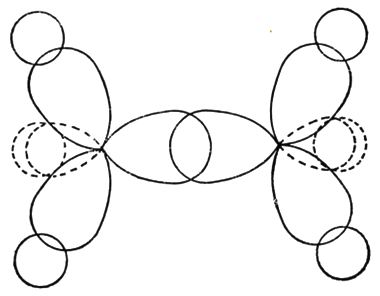
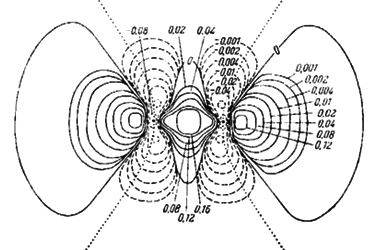
Для конструирования гамильтонианов по модели сильной и слабой связи нужно тщательно разобраться в подразделах Закон дисперсии по методу ЛКАО и Закон дисперсии в рамках kp-модели, соответственно.

Несмотря на различие двух моделей описание симметрии энергетических уровней, с точки зрения теории групп, в них одинаковое. В модели сильной связи оперируют понятиями атомных и молекулярных орбиталей; в модели слабой связи свободно парящие электроны описываются Г-состояниями кристаллической решетки (рис. 42).

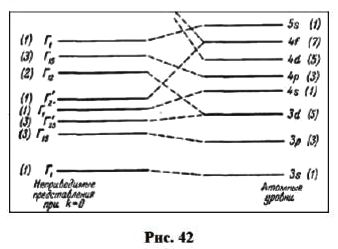
В модели сильной связи считается, что симметрия электронных уровней в кристалле определяется симметрией электронных уровней отдельных атомов, при этом умалчивается, чем, собственно, определяется симметрия уровней отдельно взятого атома. В модели слабой связи, наоборот, говорится, что симметрия электронных уровней вблизи отдельных узлов кристаллической решетки определяется симметрией всей решетки, при этом умалчивается, почему, собственно, кристаллическая решетка приобрела именно такую, а не иную симметрию. В обоих подходах отсутствует ответ об источнике симметрии для свободного атома (в модели сильной связи) и для кристаллической решетки (в модели слабой связи).

Очевидно, что источником симметрии в обоих случаях является эфир, который удобно смоделировать в виде абсолютно твердой кристаллического тела, внутри которой возникают энергетические возбуждения либо в форме свободных атомов водорода, гелия и т.д., либо связанных кристаллических решеток германия, кремния и т.д.

Известные нам кристаллы кремния, германия, арсенида галлия и т.д. образуют вторичную решетку, симметрия которой продиктована состоянием первичной решетки эфира. Но вторичная решетка при определенных условиях температуры, давления и других параметров может служить основой для возникновения производных состояний в виде экситонного газа или электронно-дырочной жидкости, которые являются сверхвеществом внутри обычного вещества.

Пара электрон-дырка описывается с помощью обычного уравнения Шредингера на языке водородоподобных состояний. Различие касается только количественной стороны дела. Так, величина радиуса Бора, энергия связи и прочие характеристики для электрона и дырки будут на порядок или два различаться по сравнению с аналогичными характеристиками в кристаллическом германии или другом полупроводнике, где экситон возникает. Для экситона кристаллическая решетка выступает в роли эффективного вакуума, т.е. нейтрального фона, который находится совершенно в другом энергетическом диапазоне, чем электроны и дырки в кристалле того же германия.

Перед тем как переходить к законам дисперсии, напомним, что понимается под k-пространством.

Если узлы прямой решетки определить равенством

R_i = n₁a₁ + n₂a₂ + n₃a₃,

то узлы обратной решетки определятся другим равенством

K_i = m₁b₁ + m₂b₂ + m₃b₃,

причем базисные векторы обоих пространств ортогональны и нормированы.

На рис. 32 показано 14 пространственных ячеек Браве.

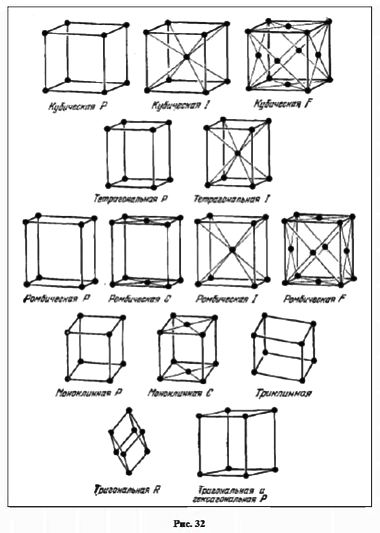
Для каждой из 14 элементарных ячеек можно построить элементарные ячейки обратной решетки.

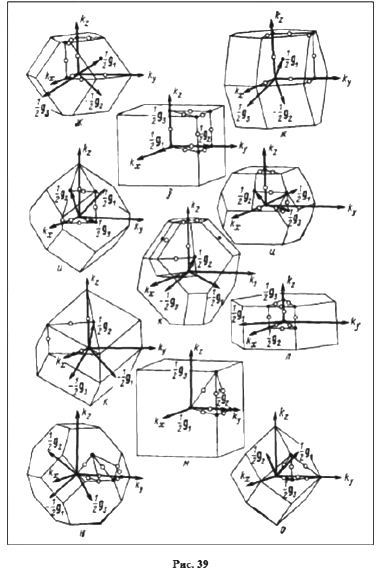
Важно уметь построить одну-единственную элементарную ячейку, поскольку закон дисперсии E_n(k) приводится только для нее одной, и здесь на первый план выдвигается понятие зоны Бриллюэна (ЗБ). Первую ЗБ определяют как область в обратном пространстве, окружающую один из узлов обратной решетки и ограниченную набором плоскостей, проходящих через середины векторов, соединяющих в обратной решетке данную точку с ее ближайшими соседями.

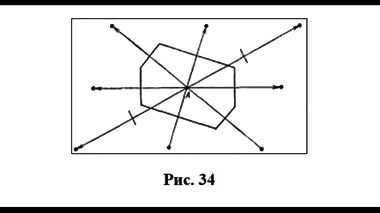
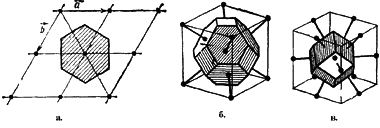
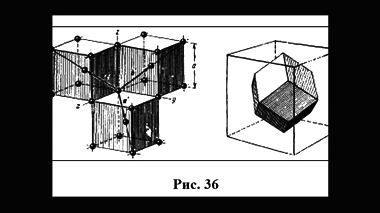
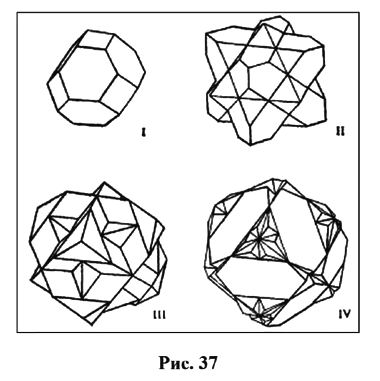
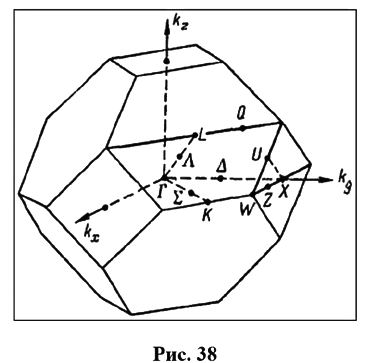
На рис. 34 показана первая ЗБ для двумерной косоугольной решетки; на рис. 35 вычерчены уже десять ЗБ для двумерной квадратной решетки. Точно таким же половинным делением расстояния между двумя узлами определяется ЗБ в трехмерном пространстве. На рис. 36а приведены базисные векторы ОЦК решетки, а на рис. 36б — первая ЗБ, имеющая форму правильного ромбододекаэдра. На рис. 37 приведены первых четыре ЗБ для ГЦК решетки. На рис. 38 указаны симметричные точки (Г, L, Λ, Δ, …) первой ЗБ для ГЦК решетки, представляющей собой полуправильный многогранник Архимеда — усеченный октаэдр. Симметричные точки и направления можно видеть на энергетических зонах, рассчитанных ЛКАО-методом (рис. 31а).

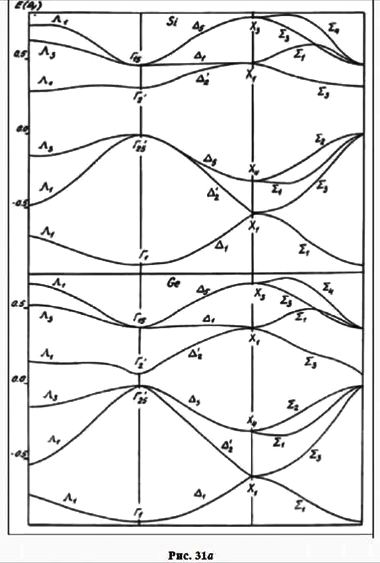
Итак, законы дисперсии (их еще именуют зонными структурами), полученные при помощи гамильтонианов, построенных на основе модели сильной связи, можно аппроксимировать кусками параболы. Законы дисперсии, полученные при помощи гамильтонианов, построенных на основе модели слабой связи, можно аппроксимировать отрезками прямых.

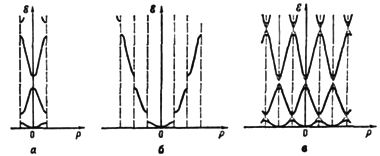
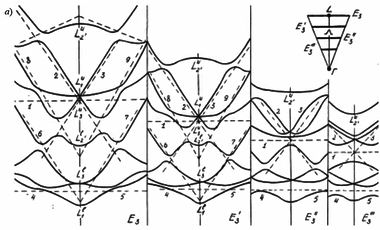
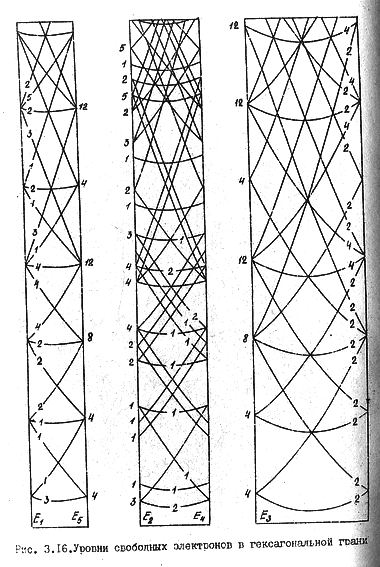
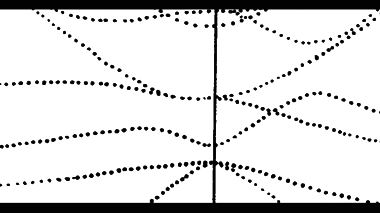
Чтобы продемонстрировать роль линейных элементов зонной структуры, обратимся к восьми нижним состояниям зоны проводимости германия на гексагональной грани зоны Брюллюэна (рис. 59). Расчет зоны производился по модели слабой связи электронов с помощью матрицы гамильтониана Г(15 × 15).

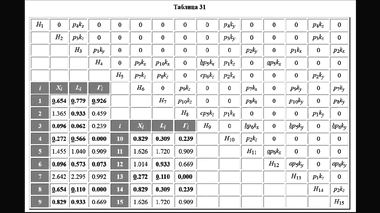
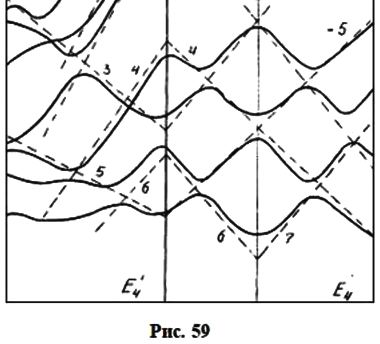
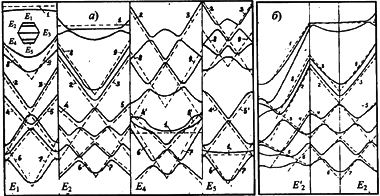
Здесь пунктирными прямыми обозначены следы от энергетических плоскостей, которые снабжены цифрами. На рис. 59а показаны четыре сечения Е₁, Е₂, Е₄ и Е₅. Два связанных сечения Е₂ и E'₂, показанные на рис. 59б, даны для того, чтобы можно было проследить связь энергетических уровней на гексагональной грани зоны Брюллюэна с уровнями, расположенными ближе к центру зоны Брюллюэна. Сечение E'₂ проведено параллельно оси k_nz.

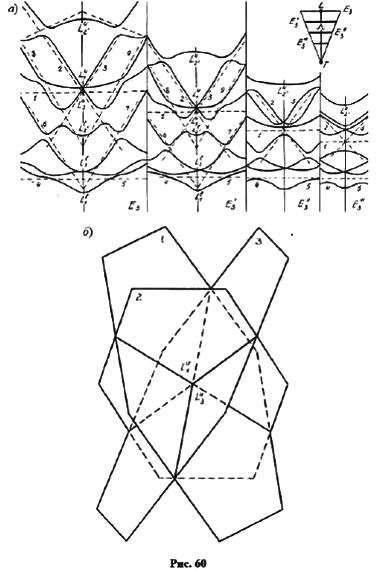
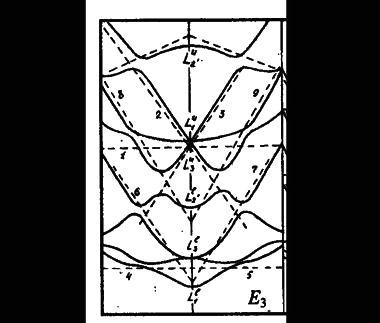
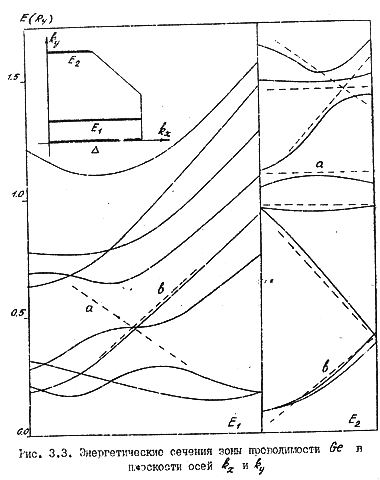
Центральное сечение E₃ изображено на следующем рис. 60а вместе с внутренними сечениями E'₃, E''₃, E'''₃, параллельными линии E₃ и проведенными в глубине зоны Брюллюэна. Общего числа сечений, представленных на рис. 59 и 60 достаточно, чтобы восстановить линейную конфигурацию восьми нижних состояний зоны проводимости германия. На рис. 60б показано пространственное расположение первых трех из восьми плоскостей.

Следующий шаг состоит в том, чтобы записать уравнения плоскостей в удобной системе координат. Первая система координат вводится на гексагональной грани ЗБ с осями Е, k'_x, k'_y. По формулам аналитической геометрии записывается в трехмерном пространстве. Однако сечения E'₃, E''₃, E'''₃ дают зоны дисперсии в глубине ЗБ и, тем самым, вводят еще одно измерение.

Три плоскости, обозначенные 1, 2 и 3, по выбранным соответствующим образом точкам можно записать в пространстве четырех измерений Е, k_x, k_y, k_z. Тогда при наличии оси симметрии третьего порядка три уравнения плоскости переходят одно в другое при циклической перестановке координат волнового вектора k_x, k_y, k_z, так что достаточно выразить линейным уравнением лишь одну какую-то плоскость. Но здесь-то как раз и возникает основная проблема, о которой мы постоянно твердили: четырехмерное пространство не существует.

Многие знают, как записать уравнение плоскости, проходящей по трем точкам, например, таким:

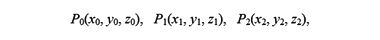
тогда уравнение плоскости получится приравниванием нулю определителя размером 3 × 3:

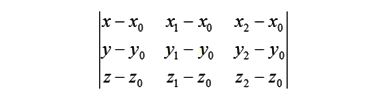
Пусть этими точками будут:

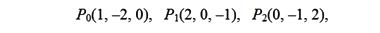
тогда определитель будет выглядеть так

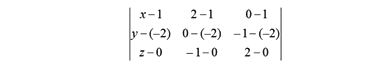
Разложим этот 3 × 3 определитель по первому столбцу на три определителя 2 × 2; в итоге получаем следующее уравнение искомой плоскости:

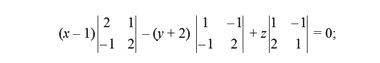
или, окончательно

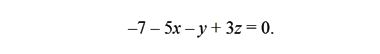
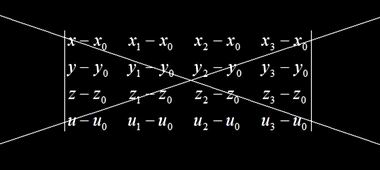
Казалось бы, почему бы нам по аналогии не построить определитель 4 × 4 — вот такого вида

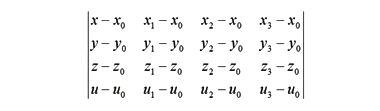
для четырех точек, взятых из конкретного закона дисперсии

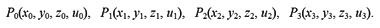
Далее, раскладываем полученный 4 × 4 определитель по первому столбцу на четыре определителя 3 × 3. Потом, повторяем эту процедуру до тех пор, пока не получим уравнение вида

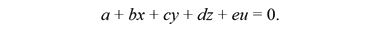
К сожалению, данное расширение формул не работает. Какие бы четыре точки вы не взяли из закона дисперсии, по ним невозможно получить уравнение плоскости в четырехмерном пространстве энергии-импульса. В процессе вычисления коэффициентов a, b, c, d, e возникает линейная зависимость между промежуточными уравнениями, так что окончательного уравнения вы не получите.

Единственное, что удается здесь получить, это некое псевдоуравнение, например, следующего вида:

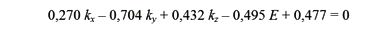
Данное уравнение есть конкретное выражение линейного закона дисперсии E_n(k) для целой группы состояний, объединенных системой трех плоскостей, но только в разрезе E₃, т.е. на гексагональной грани ЗБ. Но оно (уравнение) не дает нужные точки для плоскостей, лежащих в глубине ЗБ, т.е. в разрезах E'₃, E''₃, E'''₃.

Все рассуждения, относительно плоскостей 1, 2, 3, можно перенести на нижние плоскости, которые обозначены цифрами 4, 5, 6, 7, 4', 5'. Уравнение плоскости 6 можно получить из уравнения плоскости 7, поменяв местами переменные k_y и k_z, а координату k_x оставив без изменения. Осуществив, таким образом, перестановку координат, из этих двух уравнений получаем еще четыре. Приведем одно из них:

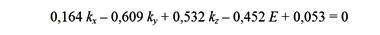
Однако это уравнение тоже описывает энергетические уровни только на гексагональной грани ЗБ E₃ и не описывает плоскости в сечениях E'₃, E''₃, E'''₃.

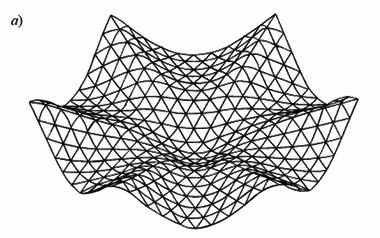
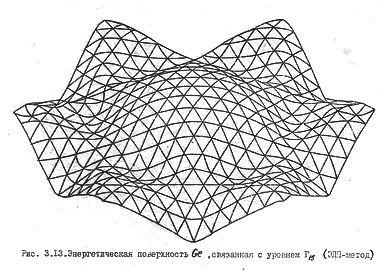
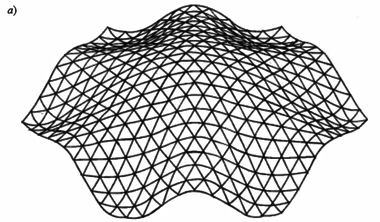
Шесть плоскостей, аппроксимирующих все нижние состояния зоны проводимости, нетрудно вычертить отдельно, как мы это уже делали для плоскостей 1, 2, 3 (рис. 60б). Однако лучшей иллюстрацией взаимного расположения этих плоскостей является графическое изображение точного машинного расчета дна зоны проводимости германия, показанного на рис. 61а. Симметрия этой поверхности для других алмазоподобных полупроводников примерно такая же.

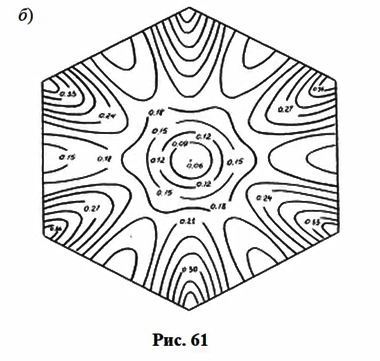
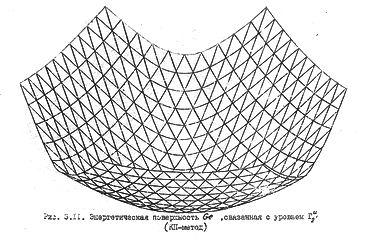
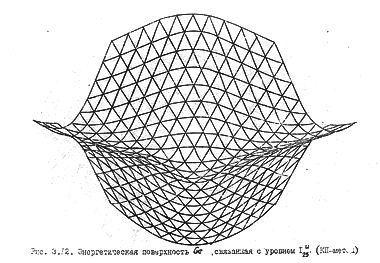
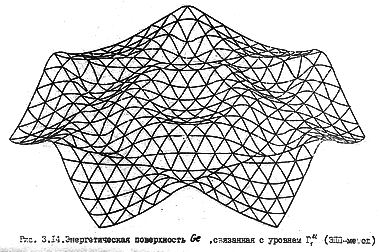
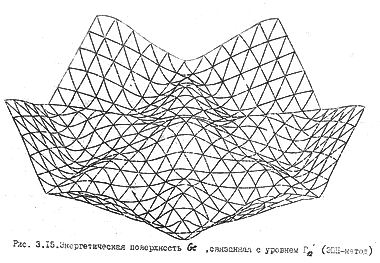
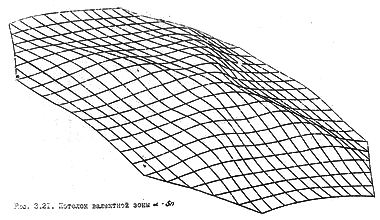
Геодезия дна зоны проводимости германия приведена на рис. 61б. Числами на линиях обозначены уровни энергии в ридбергах, отсчитанные от потолка валентной зоны ( Г '₂₅). В центре розетки находится минимум зоны проводимости. Глубина складок энергетической поверхности потолка валентной зоны меньше, чем у поверхности дна зоны проводимости (рис. 62а). Таким образом, если для дна зоны проводимости мы еще может распознать плоскости, то для потолка валентной зоны они просматриваются с трудом; здесь преобладает квадратичный элемент закона дисперсии.

Потолок валентной зоны германия

Другие энергетические уровни.

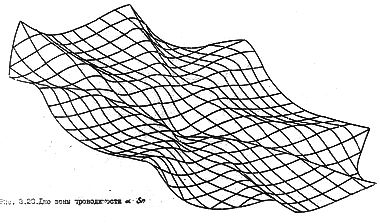
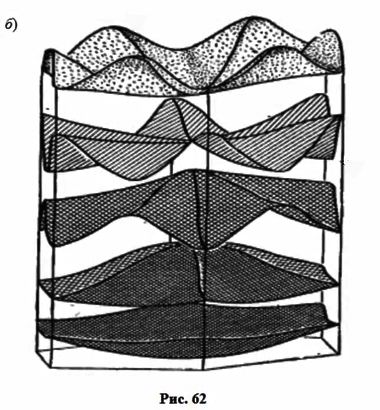
Общая структура энергетических зон в гексагональной плоскости первой ЗБ для полупроводников IV группы изображена на рис. 62б.

Смотрите фильм с этим текстом:

http://youtu.be/lrJG-J7i1Sk