О.Е. Акимов

Конструктивное познание (Часть 20)
Гиперкомплексные системы

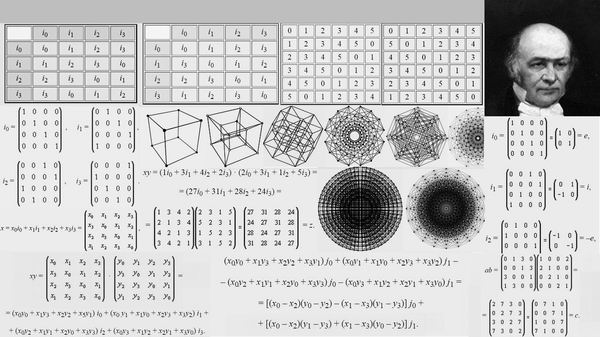
Чтобы ближе подступиться к теме многомерности пространств, нам нужно освежить в памяти некоторые алгебраические понятия. В подразделе "Дискретной математики", который называется Представление группы кватерниона, раскрывается смысл произведения двух комплексных чисел z и z', которые могут быть представлены в трех эквивалентных формах.

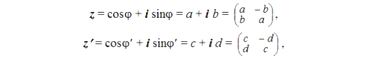
Тогда произведению z на z' отвечают два последовательных поворота в комплексной плоскости x, iy :

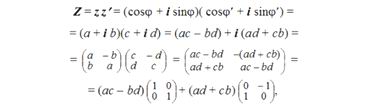
Кватернион получается путем удвоения комплексного числа: кватернион

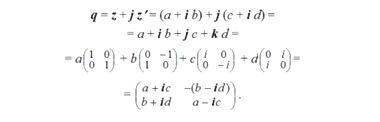
Составим произведение двух кватернионов:

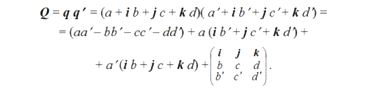
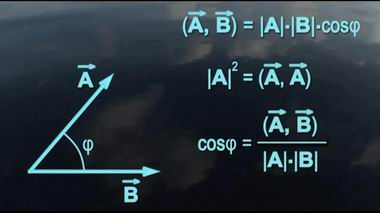
Здесь скалярная часть произведения есть произведение скалярных частей множителей минус скалярное произведение их векторных частей. Векторная часть произведения состоит из суммы произведений скалярной части каждого множителя на векторную часть другого плюс произведение векторной части первого множителя на векторную часть второго. Таким образом, все существующие виды умножения в векторной алгебре являются осколками единой операции перемножения двух кватернионов.

Перемножение двух сопряженных кватернионов дает скаляр

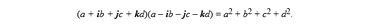
Кватернион с нормированными коэффициентами

a² + b² + c² + d² = 1,

можно представить через тригонометрические функции

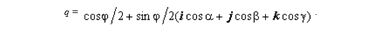
где α, β, γ — углы между некоторым вектором p и осями координат, φ — угол вращения вокруг вектора p.

Пространственное вращение, описываемое кватернионом q, за которым следует вращение q', дает результирующее изменение ориентации, описываемое кватернионом Q. Предположим, кватернион q отвечает повороту вокруг оси x на угол φ = π/2, а q' — точно на такой же угол, но вокруг оси y, что соответствует следующим формулам

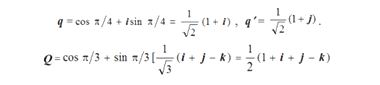
Известны две других формулы задания вращения в трехмерном пространстве: либо через направляющие косинусы:

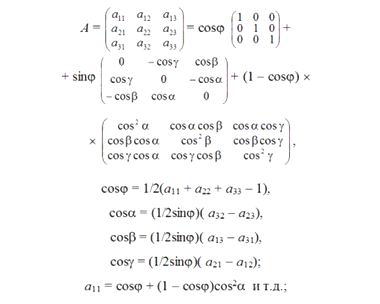
либо через углы Эйлера

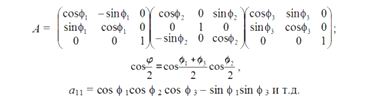
Таким образом, ортогональные повороты в трехмерном пространстве можно описывать тремя способами: непосредственно через кватернион, через 3 х 3 матрицы с направляющими косинусами и через 3 х 3 матрицы с углами Эйлера. Однако никто пока не вывел аналогичные формулы для четырехмерного пространства.

Почему? Да потому что их не существует в математической природе. Релятивисты могут сколько угодно говорить о многомерных пространствах, но математики-конструктивисты знают, что их предмет исследования не произволен. Его нельзя строить по свободной экстраполяции, когда расширение пространства действия определяется простым увеличением пространственных осей (см. К вопросу о размерности).

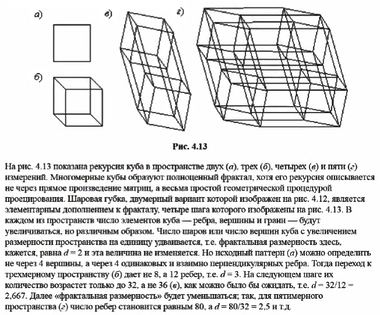
Мы не вправе по своему желанию выдумывать геометрические пространства любой размерности. Это связано с алгеброй групп. Существует геометрия на плоскости: ей ставится в соответствие алгебра комплексных чисел; существует геометрия в пространстве трех измерений: ей отвечает алгебра кватернионов. Но алгебраической структуры, отвечающей четырехмерное пространство, уже не существует.

В самом деле, удвоение кватерниона порождает октаву

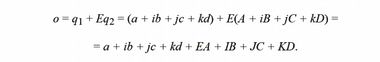
но множество октав уже не образует группы, так как умножение базисных единиц, представленное таблицей 2.50

не является ассоциативным

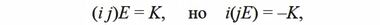
Напомним, алгебраической группой называется замкнутое множество, в котором есть единичный элемент, обратные элементы для всех прямых и выполняется закон ассоциативности, который на множестве октав как раз и нарушается (см. Определение группы и примеры групп).

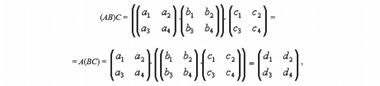
Дальнейшая экстраполяция — удвоение октавы и т.д. — тоже не приводит к числовым агрегатам, имеющим групповые свойства. Следовательно, многомерные пространства — пяти, шести и т.д. измерений — тоже существовать не могут, как и пространство четырех измерений. Есть множества, в которых закон ассоциативности выполняется, они, однако, не образуют группы. Так, в квантовой физике часто приходится иметь дело с матрицами Паули, которые в математике называются спинорами

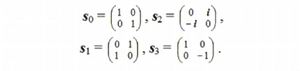
Существует простая связь между спинорами и матрицами базисных единиц кватерниона

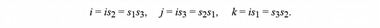
Закон ассоциативности для матриц Паули выполняется в силу общей природы матриц

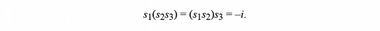
Но группы из них не получается, поскольку множество открыто, а группа должна быть замкнутой на себя. Тем не менее, на них можно построить полезную для физики математическую структуру — алгебру Клиффорда. На матрицах Паули она представляет собой следующий числовой агрегат

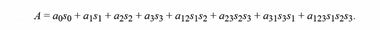
В состав агрегата A входит один скаляр, три вектора, три бивектора и один тривектор (или псевдоскаляр). При перемножении таких агрегатов будут возникать два типа умножения базисных единиц — внутреннее (или скалярное) и внешнее (или векторное).

Примерами внутреннего и внешнего произведений являются дивергенция и ротор, соответственно

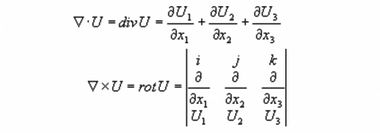
Продемонстрируем силу алгебры Клиффорда на примере электродинамики.

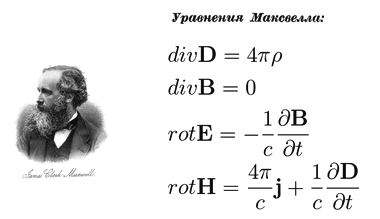
В ней вектор напряженности электрического поля (E) определяется через градиент скалярного потенциала (φ)

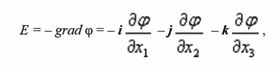
а бивектор напряженности магнитного поля (H) определяется как ротор векторного потенциала (a):

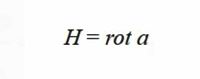
Тогда через клиффордово произведение можно дать все четыре уравнения Максвелла для статического электромагнитного поля:

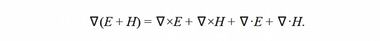
Приведем расшифровку четырех слагаемых

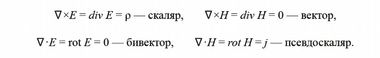
Для динамического случая изменение магнитного поля приводит к возникновению ротора электрического поля, а изменение электрического поля — ротора магнитного поля.

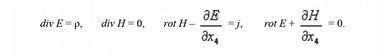
Эти же уравнения, расписанные по четырем составляющим, выглядят следующим образом

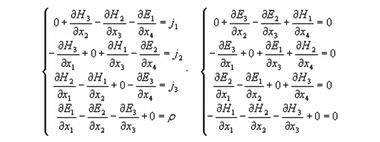
Эти две системы уравнений можно представить в матричной форме

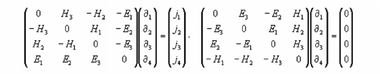
Здесь принято

∂_i = ∂/∂x_i, ct = x₄        и        j = ρv        или

(j₁, j₂, j₃, j₄) = ρ(∂x₁/∂x₄, ∂x₂/∂x₄, ∂x₃/∂x₄, ∂x₄/∂x₄)

Для получения полной симметрии в матрицы и, следовательно, в уравнения Максвелла нужно ввести мнимость, как показано здесь.

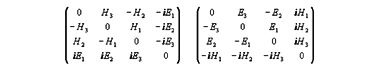
Представленный здесь формализм, кажется, имеет дело с четырехмерным пространством. Но это только кажется. Необходимо помнить, что уравнения Максвелла, описанные при помощи кватернионов, касаются трехмерного пространства. Теперь от электромагнетизма перейдем к механике.

*
*   *

Итак, по аналогии можно, конечно, написать выражение для определения расстояния между двумя точками x и y в каком-нибудь n-пространстве:

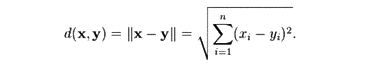
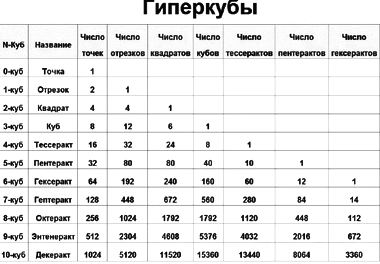
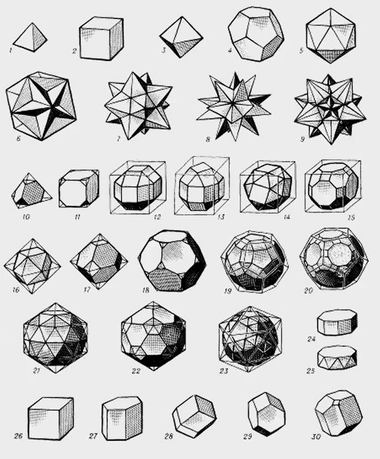
Можно вычертить n-куб или n-сферу в n-мерном пространстве. Можно даже подсчитать у них число вершин и ребер или число параллелей и меридианов. Но какое отношение всё это имеет к реальному миру физики? Ровным счетом — никакого!

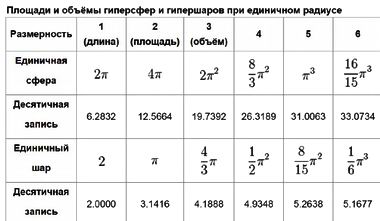
Кажется, что закон дисперсии можно представить в четырехмерном пространстве энергии-импульса, где одна ось отводится под энергию, значение которой выражается действительным (или, вещественным) числом, а три оставшиеся оси с мнимыми ортами i, j, k отводятся под импульс. Некоторые релятивисты в спорах со мной утверждали, что само слово "кватернион" означает четыре. Значит, говорили они, это гиперкомплексное число образует векторное пространство размерности четыре.

Никогда не спорьте с релятивистом; это вредно для вашего здоровья.

Верно, что ирландский математик Уильям Гамильтон в 1843 году, находясь на мосту Брум Бридж в Дублине, открыл гиперкомплексное число с четырьмя базисными единицами — одной вещественной и тремя мнимыми. На мосту установлена памятная доска с надписью «Здесь на прогулке, 16 октября 1843 года, во время вспышке гениальности, сэр Уильям Роуэн Гамильтон открыл формулу перемножения базисных единиц кватерниона

Уильям Гамильтон

Памятная доска

История открытия кватерниона была долгой и началась она с введения комплексного числа. В течение 17-го века в трудах Лейбница, Муавра, Котса, Эйлера, Даламбера, Гаусса и других математиков это понятие конкретизировалось и успешно применялось в различных областях знаний. В течение длительного времени математики безуспешно пытались построить алгебраический объект с одной вещественной и двумя мнимыми единицами, но у них ничего не получалось. И вот Гамильтон, отказавшись от трехчленного базиса, решил поэкспериментировать с четырьмя базисными единицами.

Его неожиданный успех заставил прочих математиков крепко задуматься: из скольких базисных единиц можно построить полноценное пространство. В 1877 году Георг Фробениус доказал теорему, что гиперкомплексного числа на базе трех единиц построить невозможно. Вторая половина 19-го века — это время интенсивного развития алгебры, в том числе векторной.

Уильям Клиффорд

Лондонский университет

Королевское общество

Максвелл применил кватернионы для описания законов электродинамики — о чем мы уже знаем. 26-летний Уильям Клиффорд по рекомендации Максвелла был зачислен на кафедру математики и механики Лондонского университета, а в 1874 году он стал членом Королевского общества. Еще через два года он уже докладывал об успехах своей алгебры, о которой мы рассказывали, а также о системе, построенной на бикватернионах. Окончательно аппарат векторной алгебры сформировался в последнем десятилетии 19 века в трудах Гиббса и Хевисайда.

Гиббс

Хевисайд

Работы Минковского, Борна и других релятивистов лежат где-то примерно в той же самой плоскости, что и алгебраистов 19-го века. Они хотели придумать что-то наподобие векторной алгебры для теории относительности, которая замышлялась как физика, существующая в пространстве четырех измерений. Увы, у них ничего не вышло; всё было перепахано вдоль и поперек задолго до них. Первоклассные математики 19-го столетия однозначно показали: кроме кватернионов, нет других алгебраических систем, которые бы можно было применить для реального физического мира. Минковский и Борн создали совершенно не жизнеспособную геометрию, изобилующую грубыми математическими ошибками, о которых мы говорили ранее.

Сегодня по проложенной ими кривой дороже устремились нынешние релятивисты, предложившие пространство 10 измерений. Обреченность таких построений вытекает хотя бы из того печального факта, что в основу своих построений они заложили мертворожденное четырехмерное пространство Минковского.

*
*   *

Сталин, Иосиф Виссарионович, Председатель Совета министров СССР, многолетний лидер Советского государства.

Сталин, Иосиф Виссарионович

Фадеев Александр Александрович, автор романа "Молодая гвардия", генеральный секретарь, а потом и председатель правления Союза писателей СССР, в создании которого, начиная с 1932 года, он принимал активное участие.

Фадеев Александр Александрович

Рассказывают, будто Сталин однажды сказал Фадееву: "Нет у меня для вас других пространств, кроме трехмерных".

Сталин шутит

Шутка.

*
*   *

В нашей стране существует большая группа исследователей, куда входит немало кандидатов наук, докторов, профессоров университетов, специалистов научно-исследовательских институтов, которые занимаются гиперкомплексными системами — так они определили сферу своих интересов, образовали научно-исследовательский институт, периодически проводят научные конференции по данной теме, нередко приглашают на них иностранных специалистов.

Я считаю, что направление исследований, избранное этой группой товарищей, ложное; ошибочна основная идея, которую ставит перед собой группа, учрежденный ею институт в качестве цели. Неверны также средства достижения этой цели, в частности, математический аппарат, который опирается на гиперкомплексные числа. Так как этот раздел математики входит в мой курс "Дискретной математики", который я собираюсь представить в форме видео-файла, то хочу высказаться по поводу работы Института гиперкомплексных систем (фрагмент фильма).

Эти "гиперкомплексные" ученые пытаются избранный ими математический аппарат использовать для объяснения мироздания. Я критикую философию универсализма в принципе: нельзя с помощью какого-то раздела математики объяснить все процессы, происходящие в природе. А главное, что избранный им раздел — гиперкомплексные систы — был перепахан вдоль и поперек задолго до внезапно пробудившегося в нашей стране интереса к нему. Там нет неисследованных уголков — тем более таких, в которых бы скрывались математические тайны мироздания. Всё это напоминает мне бесконечные рецидивы с возрождением почитания учения платоников и пифагорейцев.

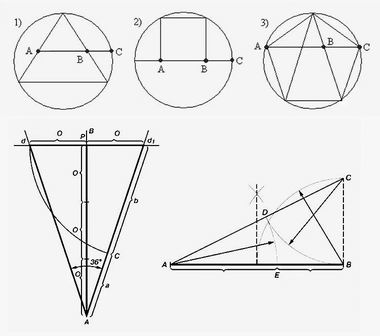
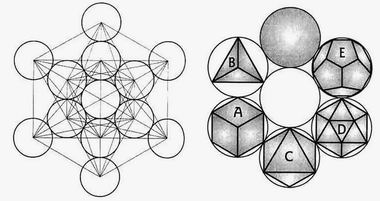
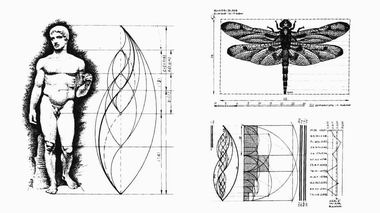
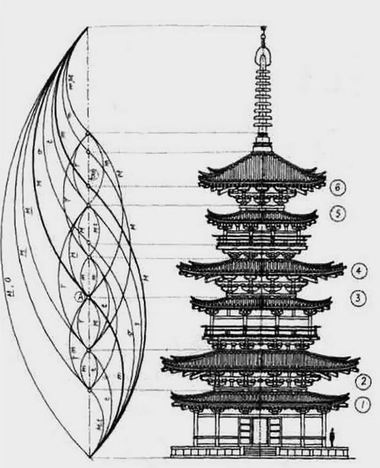
В нашей стране есть большая группа исследователей, которых можно обозначить как гармонисты-золотоискатели. Все их концептуальные построения вертятся вокруг золотого сечения, так называемой "божественной пропорции" или, если говорить в более широком, философском смысле, вокруг предустановленной гармонии. Они видят в гармонии вообще и золотой пропорции в частности, ключ ко всем тайнам мироздания

Увы, нет такой всеобщей и универсальной формы. На путях ее розыска люди делают множество ошибок, натяжек, спекуляций. Довольно банальным вещам придают чрезмерное значение. Например, числам π и е, числам Фибоначчи, комплексным числам, кватерниону, бикватерниону, гиперкомплексным числам, числовым агрегатам типа Клиффорда, матрицам Паули, тензором кривизны, многообразным геометрическим объектам — платоновым телам, кругу, сфере, гиперкубу, гиперсфере, фракталам.

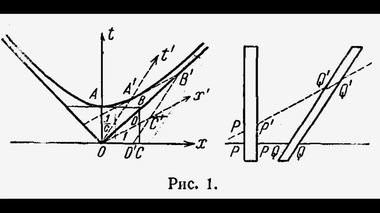
Релятивисты прошлого столетия свихнулись на дифференциальной геометрии Римана, придумали четырехмерное пространства Минковского, которое в принципе существовать не может. Кто этого не понимает, тот не понимает, вообще, математики — элементарной. Преобразования Лоренца могут повернуть вектор (какой-либо природы) только в двумерном пространстве, т.е. на плоскости, кватернион вертит векторы в трехмерном пространстве. Четырехмерного пространства не существует, тем боле 5, 6 ... 10 мерных пространств нет.

http://youtu.be/BBU2sF7dy1M


http://youtu.be/Qhz9wRqT6aU

Сегодняшние гиперкомплексанты свихнулись на финслеровой геометрии, которая, не смотря на свою четырехмерную претензию, очень ограничена по своим возможным формам. Во всяком случае, она намного беднее двумерных комплексных чисел и трехмерных кватернионов. Несчастные гиперкомплексанты напоминают мне рыб, выброшенных на берег: высоко подпрыгивают, крутятся, бьют хвостом о землю, широко открывают рот, но ничего сказать не могут. В итоге, мы видим какие-то тривиальные вещи. Их чертежи и формулы не выходят за границы аж позапрошлого столетия. По сути, они льют в старые меха приготовленное ими вино, которое кислое, некрепкое, совсем, совсем невкусное.

Смотрите фильм с этим текстом:

http://youtu.be/-j5x70m5vls