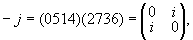Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.2. Группы на матрицах и подстановках

Представления группы кватерниона

Из групп восьмого порядка осталась не рассмотренной группа кватерниона . Если в качестве базиса взять векторы:

0 = (1, i),     1 = (– 1, –i),    2 = (i, 1),     3 = (–i, – 1),

4 = (1, –i),    5 = (–1, i),     6 = (–i, 1),    7 = (i, –1),

то они породят операционное множество, образующее двухмерное неприводимое представление:

Группа кватерниона , как и группа диэдра , состоит из пяти классов —

C₀ = {e}, C₁ = {–e}, C₂ = {i, –i}, C₃ = {j, –j}, C₄ = {k, –k},

следовательно, одномерные представления — E₀, E₁, E₂, E₃ — у нее совпадают с предыдущим случаем (табл. 2.48).

В разделе, который называется «Геометрическая интерпретация групповых преобразований», нельзя не сказать о важнейшей интерпретации произведения двух кватернионов. Подобно тому, как произведению двух комплексных чисел —

отвечают два последовательных поворота в плоскости x, iy:

произведению кватернионов соответствуют последовательные вращения в пространстве трех измерений.

Кватернион, как мы уже знаем, получается за счет удвоения комплексного числа или на базисных матрицах, которые могут иметь следующий вид:

Составим произведение двух кватернионов:

Здесь скалярная часть произведения есть произведение скалярных частей множителей минус скалярное произведение их векторных частей. Векторная часть произведения состоит из суммы произведений скалярной части каждого множителя на векторную часть другого плюс произведение векторной части первого множителя на векторную часть второго. Таким образом, все существующие виды умножения в векторной алгебре являются осколками единой операции перемножения двух кватернионов.

Перемножение двух сопряженных кватернионов дает скаляр:

(a + ib + jc + kd)(a – ib – jc – kd) = a² + b² + c² + d².

Кватернион с нормированными коэффициентами:

a² + b² + c² + d² = 1,

можно представить через тригонометрические функции:

q = .

где α, β, γ — углы между некоторым вектором p и осями координат, φ — угол вращения вокруг p.

Пространственное вращение, описываемое кватернионом q, за которым следует вращение q', дает результирующее изменение ориентации, описываемое кватернионом Q. Предположим, кватернион q отвечает повороту вокруг оси x на угол φ = π/2, а q' — точно на такой же угол, но вокруг оси y, что соответствует формулам:

Таким образом, результирующее вращение Q происходит на угол 2π/3 вокруг вектора p с направляющими косинусами, равными .

Известны другие формулы задания вращения в трехмерном пространстве. Так, матрицу A в линейном преобразовании (2.1) можно выразить либо через направляющие косинусы:

либо через углы Эйлера:

Если перемножать две матрицы A и B, то результирующая матрица C будет иметь вид исходных матриц сомножителей, т.е. закон замкнутости здесь тоже действует. В силу ассоциативности и существования обратных матриц можно говорить о бесконечных непрерывных группах поворотов векторов в трехмерном пространстве.

Итак, ортогональные повороты в трехмерном пространстве можно описывать тремя способами: непосредственно через кватернион, через 3х3-матрицу с направляющими косинусами и через 3х3-матрицу с углами Эйлера. Однако никто пока не вывел аналогичных формул для четырехмерного пространства. Почему? Да потому что их не существует. Есть такие геометрические задачи, которые, в принципе, решить невозможно. Например, нельзя построить квадрат, площадь которого была бы равна заданной площади круга. Это связано с тем, что площадь круга выражается через трансцендентное число 3,14…, которое нельзя отложить на прямой линии. Невозможность построения четырехмерного пространства является ответом на задачу подобного типа.

Чтобы почувствовать запрет на построение физических объектов в 4D-пространстве обратитесь к странице Линейная аппроксимация закона дисперсии. Здесь дается описание линейных элементов закона дисперсии, которые можно представить линейным уравнением, например, следующего вида:

0,270 Kx – 0,704 Ky + 0,432 Kz – 0,495 E + 0,477 = 0.

Однако описать квадратичные элементы или дать полное описание закона дисперсии в 4D-пространстве не удается. Разложение на минорные 3х3-матрицы для этого случая невозможно в силу обращения всех миноров в ноль как при их линейной зависимости.

Таким образом, математики-формалисты могут сколько угодно говорить о многомерных пространствах, но математики-конструктивисты знают, что их предмет исследования не произволен, его нельзя строить по свободной экстраполяции, когда расширение пространства действия определяется простым увеличением параметров, как выражение бинома Ньютона. Об успешном завершении построения псевдоевклидовой геометрии четырехмерного пространства Минковского можно будет говорить не раньше, чем будут найдены конкретные 4х4-матрицы поворотов 4-векторов.

Трудно сказать, почему геометры не обращают внимание физиков на очевидный геометрический факт: преобразования Лоренца планарные или плоские. Мы можем, конечно, написать преобразования, затрагивающие ось времени t и произвольно выбранную в пространстве трех измерений ось l(x, y, z), однако двумерная сущность преобразований сохранится. Это связано с тем, что преобразования теснейшим образом связаны с параметром скорости v = l/t, в формулу которой может входить только две переменные — l и t. В теории относительности постулируется постоянство одной из скоростей — скорости света c. Следовательно, все остальные отношения l/t должны трансформироваться так, чтобы c = const. Это приводит к тому, что две переменные, l и t, изменяются по известному закону.

С точки зрения математики, физики начала ХХ века допустили ошибку, превратив переменную t в четвертую ось некоторого «четырехмерного образования», так как в этом случае скалярная величина t превратилась в векторную величину t с соответствующим базисным ортом h. Этого нельзя было делать по двум причинам. Во-первых, скорость v, как вектор, требует, чтобы величина l тоже была векторного характера (она и есть радиус-вектор l), но при этом величина t должна оставаться скалярной величиной, так как математические объекты типа вектор = вектор/вектор существовать не могут.

Во-вторых, мы не вправе по своему желанию выдумывать геометрические пространства любой размерности (это связано с алгеброй групп). В частности, существует геометрия на плоскости: ей ставится в соответствие алгебра комплексных чисел вида a + ib; существует геометрия в пространстве трех измерений: ей отвечает алгебра кватернионов вида a + ib + jc + kd. Однако не существует ни геометрия, ни алгебра образований типа a + ib + jc или a + ib + jc + kd + le. Интерпретаторы теории относительности преподносят дело так, будто физики оперируют 4-векторным пространством: ht + ix + jy + kz. Однако это геометрическое образование абсолютно нежизнеспособно. Иные интерпретаторы четырехмерный пространственно-временной континуум ассоциируют с кватернионом t + ix + jy + kz и также ошибаются, так как повороты в таком пространстве ортогональны и все три орты, i, j, k, не изменяют своей метрики.

Таким образом, четырехмерного пространства не существует. Объяснение этому фундаментальному математическому факту необходимо искать в алгебре числовых агрегатов. Выше мы видели, что комплексному числу ставится в соответствие плоскость. Удвоенное комплексное число дает кватернион, которому соответствует трехмерное пространство. Удвоение кватерниона порождает октаву (см. следующий подраздел), которой, однако, не отвечает четырехмерное пространство, поскольку октава не образует алгебраической группы. Дальнейшая экстраполяция — удвоение октавы и т.д. — тоже не приводит к числовым агрегатам, имеющим групповые свойства. Следовательно, многомерные пространства — пяти, шести и т.д. измерений — тоже существовать не могут, как и пространство четырех измерений.

В конце 60-х годов XIX века и в последующие года в связи с повышенным интересом к геометрии немало говорилось о многомерности и неевклидовости физического пространства. Именно эту формальную возможность физики-теоретики использовали в теории относительности. Однако в реальном мире никакого четырехмерного пространства не существует. Преобразования Лоренца действуют только в пределах плоскости, мы не можем их распространить даже на трехмерное пространство. До возникновения релятивистского учения в 1895 году Герберт Уэллс написал фантастический роман «Машина времени», который пользовался огромной популярностью в мире. Теория Эйнштейна является прямым отражением общественных ожиданий существования четырехмерного пространственно-временного континуума (см. «Машина времени»).

Для более детального знакомства с данной проблематикой рекомендуем внимательно ознакомиться со следующими подразделами «Дискретной математики». О связи преобразований Лоренца (гиперболический поворот) с преобразованиями Декарта (ортогональный поворот) читайте в подразделе Ортогональные и гиперболические преобразования; истинная формула изменения эталонов длины и времени приведена в подразделе Масштаб осей при гиперболическом повороте, о невозможности сведения преобразований Лоренца к преобразованиям Галилея написано в подразделе Две симметрии: вращение и перемещение и, наконец, к теме СТО относится вопрос Инвариантность волнового уравнения, с которым тоже полезно ознакомиться.