Cвойства жидкости

Плотность жидкости ρ определяется как отношение массы Δm к занятому ею объему ΔΩ (в СИ измеряется в кг/м³):

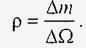
В произвольной точке жидкости плотность определяется пределом:

.

Плотность зависит от температуры и давления; в частности, зависимость плотности воды от ее температуры при нормальном атмосферном давлении показана в табл. 1.

		Таблица 1

t °С	ρ кг/м³		t °С	ρ кг/м³

0	999,87		30	995,76
2	999,97		35	994,13
4	1000,0		40	992,35
6	999,97		50	988,20
8	999,88		60	983,38
10	999,75		70	977,94
15	999,15		80	971,94
20	998,26		90	965,56
25	997,12		100	958,65

Свойство жидкостей изменять свой объем при изменении давления называется сжимаемостью. Она характеризуется коэффициентом объемного сжатия β_Ω , который представляет собой относительное изменение объема жидкости ΔΩ / Ω при увеличении давления на единицу ΔP :

;

Давление и напряжение в СИ измеряется в паскалях (Па): 1 Па = 1 Н/м² = 10 дин/см² = 0,0075 мм рт. ст. Далее мы часто будем использовать единицу измерения атмосфера (атм): 1 атм = 101325 Па = 760 мм рт. ст. Это — так называемая физическая атмосфера, которая отличается от технической, которую часто обозначают только двумя буквами — ат: 1 ат = 735,56 мм рт. ст. = 98066,5 Па. Коэффициент β_Ω измеряется в 1/Па. Знак « – » в последней формуле указывает на то, что при увеличении давления объем жидкости будет уменьшаться.

При неизменной массе (m = const), имеем равенство:

;

следовательно, при изменении давления на единицу ΔP коэффициент объемного сжатия можно определить также через относительное изменение плотности жидкости:

.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости (измеряется в Па):

      или                   (*).

Откуда следует закон Гука для жидкостей в условиях всестороннего сжатия.

.

Величина модуля упругости Е₀ зависит от температуры и давления, поэтому жидкости не точно следуют закону Гука. В табл. 2 даны значения модуля упругости воды при различной ее температуре (справедливо для давлений — от нормального до 50 атм).

	Таблица 2

t °С	Е0 ГПа

0	999,87
10	999,97
20	1000,0
30	999,97

Для практиков приведем несколько важных характеристик. Модуль упругости минеральных масел, используемых в механизмах с гидравлическим приводом, при t = 20°С составляет 1,35 – 1,75 ГПа (меньшее значение относится к более легкому маслу), бензина и керосина — приблизительно 1,3 ГПа, глицерина — 4,4 ГПа, ртути — в среднем 3,2 ГПа. Растворы, применяемые при бурении, имеют Е₀ = 2,5 ГПа.

Сжимаемость воды незначительна: при увеличении давления на 9,81 МПа объем воды уменьшается всего на 0,0005 % первоначального объема. Поэтому воду часто считают несжимаемой средой. При этом не следует забывать, что такое допущение правомерно лишь в тех случаях, когда изменения давления невелики. В практике эксплуатации гидравлических систем отмечаются случаи, когда вследствие действия того или иного возмущения (например, резкое закрытие или открытие запорного устройства в трубопроводе) в жидкости значительно изменяется давление. В таких случаях пренебрежение сжимаемостью жидкости приводит к существенным погрешностям.

Всё познается в сравнении. Верно, что сжимаемость воды небольшая, однако она примерно в 100 раз больше сжимаемости стали. Пренебрежение сжимаемостью воды может привести к парадоксу. В самом деле, поскольку в безграничной однородной жидкости или в объеме, ограниченном абсолютно жесткими стенками, скорость распространения звука определяется выражением:

,

то с учетом выражения (*) получаем следующее соотношение для изменения плотности при изменении давления:

,

Если в этом выражении допустить, что жидкость абсолютно несжимаема, т.е. Δρ → 0, то скорость звука в жидкости окажется бесконечно большой величиной: c → ∞ , что не соответствует действительности. Скорость звука в воде огромна, но конечна. Она равна примерно 1,5 км/с (см. табл. 3 раздела Введение в акустику ).

Свойство жидкостей изменять объем при изменении температуры характеризуется температурным коэффициентом объемного расширения — β_t , который измеряется 1/K или 1/°С. При неизменном давлении этот коэффициент показывает относительное изменение объема жидкости при изменении температуры на 1°С :

.

Плотность жидкости при нагревании в результате увеличения ее объема уменьшается. Это уменьшение выражается через коэффициент объемного расширения β_t по следующей формуле:

.

где ρ₀ — плотность жидкости при температуре t₀ . Коэффициент β_t с увеличением давления для большинства жидкостей также уменьшается. Но для воды эта зависимость выглядит сложнее. О не простом изменении коэффициента β_t от температуры и давления дает представление табл. 3, где приведены средние значения коэффициента объемного расширения для воды (в единицах 1/K) при трех давлениях (P = 1, 100 и 500 атм) и в пяти температурных диапазонах, указанных в первом столбце таблицы.

		Таблица 3

t °С	P=1	P=100	P=500

1-10	0,140	0,430	1,490
10-20	0,150	0,165	0,236
40-50	0,420	0,422	0,429
60-70	0,556	0,548	0,523
90-100	0,719	  —	0,661

Как видим, в диапазоне температур 10-20 °C наблюдается резкое снижение коэффициента β_t , но с ростом давления абсолютная величина этого провала всё же становится меньше.

В табл. 4 приведены значения β_t для некоторых жидкостей при комнатной температуре t = 20 °С и нормальном атмосферном давлении (P = 1 атм).

	Таблица 4

βt 1/K	Жидкость

0,15	Вода
0,18	Ртуть
0,50 	Глицерин
0,60	Нефть
1,10	Спирт

В практическом плане важно помнить, что при обычном уменьшении плотности нефтепродуктов (с 920 до 700 кг/м³) коэффициент β_t увеличивается очень незначительно. Поэтому для рабочих жидкостей в гидросистемах коэффициент β_t обычно принимают не зависящим от температуры. Для таких жидкостей рост давления от атмосферного до 60 МПа приводит к увеличению коэффициента β_t примерно на 10 – 20 % , причем чем выше температура рабочей жидкости, тем значительнее увеличение коэффициента β_t .

Переходим к следующей важной характеристике жидкости — вязкости. Под ней понимается свойство жидкости оказывать сопротивление относительному сдвигу ее слоев. Вязкость возникает благодаря межмолекулярному взаимодействию, что иногда называют просто трением молекул внутри жидкости или внутренним трением. Трение между молекулами (слоями) и, тем самым вязкость жидкости, можно легко представить на примере следующей математической модели.

В некоторых расчетах вязкость жидкости можно не учитывать. В этом случае жидкость называют идеальной. Если рассматривать течение этой идеальной жидкости внутри цилиндрической трубы, то скорости всех ее молекул в сечении AB будут одинаковыми (рис. 1, слева). Распределение скоростей молекул для реальной жидкости, когда учитывается ее вязкость, представляет собой параболу (рис. 1, справа). В точках A и B скорость молекул равна нулю; по оси цилиндра в центре трубы она окажется максимальной.

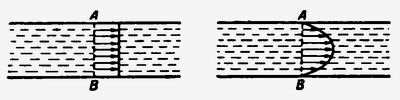
Рис. 1. Скорости распределения молекул
для идеальной (слева) и реальной (справа) жидкостей

Рассмотрим слоистое прямолинейное движение жидкости в цилиндрической трубе круглого поперечного сечения (рис. 2 слева). Жидкость движется концентрическими цилиндрическими слоями толщиной dr. За счет трения о неподвижные стенки трубы скорость слоев распределена по параболе. Разность скоростей в соседних слоях равна dV. На поверхностях соприкосновения слоев возникают силы внутреннего трения. Рассмотрим элементарный срез объема жидкости (рис. 2 справа).

   

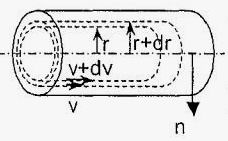
Рис. 2. Слоистое движение жидкости в трубе (слева);
деформация элементарного слоя жидкости (справа)

В соответствии с рис. 2, имеем следующее соотношение:

,

где величина dV/dn есть градиент скорости по нормали к оси потока. При слоистом движении скорость деформации сдвига равна градиенту скорости:

.

Тогда касательное напряжение определяется по формуле

,

где μ — коэффициент динамической вязкости жидкости. В зависимости от выбора направления отсчета расстояний по нормали (от стенки рассматриваемой трубы или от ее оси) градиент скорости может быть положительным (расстояние отсчитывается от стенки) или отрицательным (расстояние отсчитывается от оси трубы). Знак в формуле принимается таким, чтобы касательное напряжение было положительным. Вязкость жидкостей измеряют с помощью вискозиметров различных типов и конструкций.

В естественных условиях и в промышленном производстве существует большое разнообразие вязкопластичных сред: бетонные гидросмеси, строительные растворы, растворы полимеров, коллоидные суспензии, гидросмеси из глины, илов, мела, цемента и т.д. В таких случаях к касательному напряжению τ может добавляться некоторая ощутимая поправка τ₀ :

,

Таким образом, эти жидкости даже в состоянии покоя (dV/dn = 0) обладают ненулевым значением касательного напряжения.

Динамическая вязкость μ зависит от температуры и давления жидкости. Для чистой воды зависимость динамической вязкости от температуры, предложенная Ж. Пуазёйлем (1799 – 1869), имеет вид

,

где t — температура, меняющаяся в пределах от 0 до 90 °С; μ₀ — динамическая вязкость при t = 0 °С; коэффициент μ измеряется в единицах Па · с. В память французского ученого единица динамической вязкости была названа пуаз (П). В системе СГС 1 П = 1 г/(см · с). Единица динамической вязкости в СИ: Па · с; 1 Па · с = 10 П.

В табл. 5 приведены значения динамической вязкости воды при различной температуре.

		Таблица 5

t °С	μ мПа·с		t °С	μ мПа·с

0	1,78		40	0,66
5	1,52		50	0,55
10	1,31		60	0,47
15	1,14		70	0,41
20	1,01		80	0,36
30	0,80		90	0,32

Кроме динамической вязкости в расчетах используется кинематическая вязкость, равная отношению динамической вязкости к плотности жидкости:

,

где плотность жидкости (ρ) можно выразить через конкретные значения температуры (T) и давления (P):

,

Здесь индекс « 0 » относится к нормальным атмосферным условиям. Название «кинематическая вязкость» отражает тот факт, что в размерность величины ν входят только кинематические, но не динамические, величины. В СИ единица кинематической вязкости — м²/с. Применяется также и внесистемная единица стокс (Ст), названная в честь английского физика Джорджа Габриеля Стокса (1819 – 1903), который долгие годы занимался гидродинамикой. 1 Ст = 1 см²/с = 10^–4 м²/с. В табл. 6 приведены значения кинематической вязкости для некоторых веществ.

		Таблица 6

Вещество	t °С	ν Ст

Воздух		0	0,133
Нефть легкая	18	0,250
Нефть тяжелая	18	1,400
Керосин		15	0,027
Мазут		18	20,00
Масло АМГ-10	50	0,100
Сталь жидкая	1550	0,0037
Ртуть		15	0,0011

Кинематическая вязкость воды, которая содержит некоторое количество мелких (менее 0,05 мм) взвешенных твердых частиц, может заметно увеличиваться по сравнению с чистой водой. Так, при t = 5 °C и количестве взвешенных частиц 100 мг/л кинематическая вязкость ν = 1,6 · 10^–6 м²/с, а при загрязнении в 600 мг/л ν = 2,0 · 10^–6 м²/с. Но при нагреве воды концентрация взвеси влияет слабо. Например, при t = 25 ° C и том же количестве взвешенных частиц 100 мг/л ν = 0,90 · 10^–6 м²/с, а при загрязнении в 600 мг/л ν = 0,92 · 10^–6 м²/с.

Все жидкости в той или иной мере поглощают и растворяют газы. Согласно закону растворимости Дальтона, при давлениях до 30 МПа и постоянной температуре относительный объем растворенного газа в жидкости (Ω_г / Ω_ж) равен постоянной величине k_p , называемой коэффициентом растворимости газа или константой Генри. Коэффициент растворимости зависит от температуры:

,

где ΔH — изменение энтальпии при растворении, R — универсальная газовая постоянная.

Процесс перехода жидкости в газообразное состояние, происходящий внутри жидкости, называется кипением. Жидкость можно довести до кипения повышением температуры до значений, больших температуры кипения при данном давлении, или понижением давления до значений, меньших давления насыщенных паров жидкости при данной температуре. Обычно при понижении давления до давления насыщенных паров жидкости (при данной температуре) в жидкости образуются пузырьки, заполненные парами жидкости или газами, выделившимися из жидкости, т.е. происходит так называемое холодное кипение. При наличии в жидкости свободной поверхности эти пузырьки всплывают и выходят наружу. В табл. 7 приведена зависимость давления насыщенных паров воды ( P_нп ) от температуры при нормальном внешнем атмосферном давлении.

			Таблица 7

t °С	Pнп кПа		t °С	Pнп кПа

5	0,87		30	4,30
10	1,23		40	7,40
15	1,70		60	20,3
20	2,33		80	48,3
25	3,20		100	103,3

В том случае, когда капельная жидкость находится в замкнутом пространстве и не имеет свободной поверхности, эти пузырьки могут, перемещаясь вместе с жидкостью, попасть в область более низкой температуры или более высокого давления. Тогда пары газов конденсируются, газы снова растворяются в жидкости, в образовавшиеся пустоты проникают частицы жидкости, что приводит к резкому схлопыванию пузырьков. В результате этого происходит повышение давления и локальное повышение температуры. Такое явление называется кавитацией. Из-за непрерывного импульсивного воздействия и повышения температуры в процессе кавитации происходит более активное разрушение поверхности стенок сосуда или трубопровода.

Газы могут находиться в жидкости в растворенном и нерастворенном виде. Присутствие в жидкости нерастворенного воздуха (или другого газа) в виде пузырьков существенно уменьшает модуль упругости жидкости, причем это уменьшение не зависит от размеров пузырьков. В жидкости, из которой удален растворенный и не растворенный газ, т.е. в дегазированной жидкости, кипение наступает при температуре, большей температуры кипения. В обычных условиях большие массы жидкости не сопротивляются растеканию или растягивающим усилиям, но в дегазированных жидкостях это сопротивление возникает. Для малых масс жидкости вступают в действие так называемые силы поверхностные натяжения.

Молекулы жидкости, находящиеся на границе с газом, твердым телом или между двумя несмешивающимися жидкостями, испытывают со стороны остальных молекул жидкости не уравновешенное извне воздействие. Под влиянием этого воздействия поверхность жидкости стремится принять форму, соответствующую наименьшей площади. В результате этого малые массы жидкости, образуя в воздухе капли (тумана или дождя), стремятся к шарообразной форме.

Чтобы увеличить поверхность жидкости, необходимо часть внутренних молекул вывести на поверхность, для чего придется совершить работу. Это можно представить как наличие сопротивления растяжению поверхности жидкости, т.е. на поверхности жидкости распределены силы, препятствующие растяжению. Эти силы, действующие по касательным к поверхности, собственно, и называются силами поверхностного натяжения.

С увеличением температуры поверхностное натяжение σ уменьшается. Вода в контакте с воздухом при температуре 20 °C и нормальном атмосферном давлении создает поверхностное напряжение σ = 0,0726 Н/м. Для этилового спирта эта величина равна 0,022; для различных смазочных масел — 0,035 – 0,038; для ртути — 0,486. Если ртуть соприкасается не с воздухом, а с водой, то при той же температуре 20 °C поверхностное натяжение на границе двух жидкостей уменьшается и равно 0,378 Н/м.

В трубках малого диаметра — капиллярах — наблюдается искривление свободной поверхности, граничащей с газом или с парами этой же жидкости. Если поверхность трубки смачивается, свободная поверхность жидкости в капилляре становится вогнутой; если смачивания нет, то свободная поверхность — выпуклая. В обоих случаях силы поверхностного натяжения обусловливают дополнительные (капиллярные) напряжения, которые заставляют жидкость либо подниматься вдоль вертикального капилляра (при смачивании), либо опускаться (если смачивание отсутствует). Величина подъема или снижения столба жидкости ( h_кап ) в капилляре диаметром d определяется по формуле Жюрена:

,

где σ — поверхностное напряжение, ρ — плотность жидкости, g — ускорение свободного падения, Θ — краевой угол смачивания (острый угол между касательной к свободной поверхности в точке пересечения со стенкой и самой стенкой капилляра).

Для чистой воды и стекла Θ ≈ 0 °; при t = 20 °C вода поднимается на высоту h_кап = 30/d, если d выражается в мм. В капиллярных термометрах в качестве рабочего вещества используется спирт и ртуть. Для них высота поднятия жидкости равна, соответственно, 11,5/d и 10,15/d, причем угол Θ близок к 45°. Поднятие воды в капиллярах почвы является важным фактором ее подачи к корням растений. В глине грунтовая вода может подняться на 5 метров. Гравий капилляры не образует, поэтому трава и деревья на нем не растут. С увеличением минерализации воды растет и высота ее капиллярного поднятия.

По сравнению с другими жидкостями вода обладает рядом уникальных свойств. Чистая вода, в целом являясь нейтральным веществом, часто выступает сильным растворителем. Эта ее способность характеризуется относительной диэлектрической проницаемостью, которая довольно высока и для дистиллированной воды: при 0 °С она составляет около 87. С ростом температуры диэлектрическая проницаемость уменьшается до 55,7 при 100 °С.

Для сравнения укажем, что у большинства других растворителей диэлектрическая проницаемость значительно ниже и меняется в пределах от 10 до 50. У так называемых неполярных жидкостей, не обладающих способностью растворять электролиты, она составляет 2–2,5. Таким образом, по сравнению с воздухом, диэлектрическая проницаемость которого равна 1, эта характеристика воды гораздо больше (для льда она равна 3,2).

Из-за присутствия в воде растворенного воздуха, богатого кислородом, и ряда агрессивных компонентов молекулы воды расщепляются на кислотные (H⁺) и щелочные (OH^–) компоненты, что приводит к электрохимической коррозии материалов. Растворенные в воде соли и взвешенные в ней твердые частицы могут привести к зарастанию стенок трубопровода ненужными отложениями, из-за которых пропускная способность его заметно снижается.

Электропроводность сухого льда и снега гораздо меньше электропроводности воды, причем электропроводность воды сильно зависит от наличия примесей, а на электропроводность льда они влияют мало. Электропроводность воды зависит от концентрации растворенных в ней солей. Поэтому электропроводность морской воды на 2-3 порядка выше, чем электропроводность пресной речной воды, и больше примерно в 12 тысяч раз, чем электропроводность химически чистой воды (при 18 °С).

Вода имеет аномально большую удельную теплоемкость — 4,18 Дж/(кг · K). Эта величина 5 раз больше, чем у известняка, в 9 раз больше, чем у железа и в 33 раза больше, чем у ртути. Таким образом, вода в озере при одинаковой температуре воздуха и одинаковом получаемом ею солнечном тепле нагреется в 5 раз меньше, чем сухой песчаный пляж на берегу озера. Однако во столько же раз вода будет дольше сохранять полученное тепло, чем песчаная почва. Океаны обеспечивают инерционность природных колебаний климата на Земле. Хорошо известно, что вблизи морей климат намного мягче, чем внутри континентов.

Вода обладает также высокой теплотой испарения (22,6 · 10⁵ Дж/кг) и скрытой теплотой плавления (3,34 · 10⁵ Дж/кг). Для перехода воды в пар при атмосферном давлении из окружающей среды требуется в 6,75 раза больше теплоты, чем при плавлении льда при том же давлении. При конденсации влаги (образовании тумана) выделяется значительное количество теплоты. Это используется в установках, создающих искусственный туман. Такие установки помимо орошения могут использоваться для предохранения растений от заморозков.

Если при плавлении твердых тел теплоемкость вещества изменяется незначительно, то при плавлении льда она увеличивается скачком более чем вдвое — от 2,052 до 4,224 кДж/кг. При нагревании теплоемкость воды сначала падает, достигая минимума 4,1809 кДж/кг при температуре 34,5 °C (напомним, нормальная температура человеческого тела равна 36,6 °C), а затем начинает снова увеличивается. Появление этого минимума объясняется полным разрушением кластеров — особых ассоциативных групп из молекул воды, показанные на рис. 3.

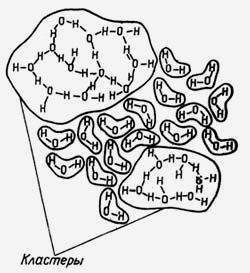
Рис. 3. В так называемой талой воде молекулы H₂O могут
объединяться в сложные ассоциации — кластеры,
по структуре напоминающие лед.

Для льда отношение длин химической связей О–Н к Н–Н равно 0,613, а угол при вершине, где находится атом кислорода, равен 109,5°. Для пара эти параметры соответственно равны 0,631 и 104,5°. В случае талой воды кластерная структура молекулы воды H–O–H образует так называемый золотой треугольник с «золотым» числом 0,618 и углом при вершине 108°. В результате этого, по мнению мистически настроенных людей, «мертвая вода» превращается в «живую», обладающую чудодейственными свойствами.

Считается, что «живая вода», улучшает обмен веществ и усиливает кровообращение, снижает количество холестерина в крови и успокаивает боли в сердце, повышает адаптационные возможности организма и способствует продлению жизни. Эзотерики уверены, глоток чистейшей талой воды тонизирует лучше пастеризованного сока — в ней заключен заряд бодрости и энергии, способные в больном организме развеять хворь и подарить ему счастливое долголетие. Если бы все эти замечательные превращения имели место быть, то биологический отбор привел бы к тому, что у человека температура тела была бы не 36,6 °C, а гораздо ниже указанного предела в 34,5 °C. Критику мистического взгляда на талую воду можно найти здесь.

---

Данный материал сверстал Олег Акимов, используя при этом текст первой главы учебника В.А. Винникова и Г.Г. Каркашадзе «Гидромеханика» (М., 2003).