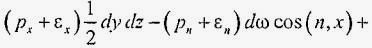Блез Паскаль (1623–1662)
В историю естествознания Блез Паскаль вошел как великий физик и математик, один из создателей математического анализа, проективной геометрии, теории вероятностей, вычислительной техники, гидростатики. Франция чтит в Паскале одного из самых замечательных писателей: «Тонкие умы удивляются Паскалю как писателю самому совершенному в величайший век французского языка... Каждая строка, вышедшая из-под его пера, почитается как драгоценный камень» (Жозеф Бертран). Далеко не все соглашались с мыслями Паскаля о человеке, его месте во Вселенной, смысле жизни, но никто не оставался равнодушным к строкам, за которые их автор заплатил жизнью и которые удивительным образом не старились. В 1805 г. Стендаль писал: «Когда я читаю Паскаля, мне кажется, что я читаю себя». А через сто лет в 1910 г. Л. Н. Толстой читал «чудного Паскаля», «человека великого ума и великого сердца» и «не мог не умилиться до слез, читая его и сознавая свое полное единение с этим умершим сотни лет тому назад человеком». Поучительно сопоставить, как старятся идеи естественнонаучные и гуманитарные.

Паскаль в юностиУпомянем еще об одной грани наследия Паскаля — его практических достижениях. Некоторые из них удостоились высшего отличия — сегодня мало кто знает имя их автора. Для И. С. Тургенева мерилами удобства и простоты были «яйцо Колумба» и «Паскалева тачка». Узнав, что великий ученый изобрел самую обыкновенную тачку, он писал Н. А. Некрасову: «Кстати я в одном месте говорю о Паскалевой тачке — ты знаешь, что Паскаль изобрел эту, по-видимому, столь простую машину». А еще Паскалю принадлежит идея омнибусов — общедоступных карет («за 5 су») с фиксированными маршрутами — первого вида регулярного городского транспорта.
В названии замечательной кривой 4-го порядка увековечено имя Этьена Паскаля (1588 – 1651) — отца Блеза Паскаля. Э. Паскаль, как было принято в роде Паскалей, служил в парламенте (суде) города Клермон-Феррана. Совмещение юридической деятельности с занятиями науками, далекими от юриспруденции, было делом нередким. Примерно в это же время посвящал математике свой досуг советник тулузского парламента Пьер Ферма (1601 – 1665). Хотя собственные достижения Э. Паскаля были скромными, его основательные познания позволяли ему поддерживать профессиональные контакты с большинством французских математиков. С великим Ферма он обменивался трудными задачами на построение треугольников; в споре Ферма с Рене Декартом (1596 – 1650) о задачах на максимум и минимум Паскаль выступал на стороне Ферма. Б. Паскаль унаследовал добрые отношения отца со многими математиками, но вместе с тем к нему перешли и напряженные отношения с Декартом.
Этьен Паскаль тщательно продумывает систему воспитания детей. На первых порах он решительно исключает математику из числа предметов, которым обучает Блеза: отец боялся, что ранняя увлеченность математикой помешает гармоничному развитию, а неизбежные напряженные размышления повредят слабому здоровью сына. Однако 12-летний мальчик, узнав о существовании таинственной геометрии, которой занимался отец, уговорил его рассказать о запретной науке.
Примерно в 10 лет Б.Паскаль сделал первую физическую работу: заинтересовавшись причиной звучания фаянсовой тарелки и проведя поразительно хорошо организованную серию экспериментов при помощи подручных средств, он объяснил заинтересовавшее его явление колебанием частичек воздуха. В 13 лет Б. Паскаль уже имеет доступ в математический кружок Мерсенна, в который входило большинство парижских математиков, в том числе Э.Паскаль (Паскали жили в Париже с 1631 г.).
Францисканский монах Марен Мерсенн (1588 – 1648) сыграл в истории науки большую и своеобразную роль ученого-организатора1. Его основная заслуга состояла в том, что он вел обширную переписку с большинством крупных ученых мира (у него было несколько сот корреспондентов). Мерсенн умело концентрировал информацию и сообщал ее заинтересованным ученым. Эта деятельность требовала своеобразного дарования: умения быстро понимать новое, хорошо ставить задачи. Обладавший высокими нравственными качествами Мерсенн пользовался доверием корреспондентов. Иногда письма Мерсенна адресовались совсем молодым ученым. Так, в 1648 г. он начал переписываться с 17-летним Гюйгенсом, помогая в его первых шагах в науке и предвещая, что тот станет «Аполлонием и Архимедом... грядущего века». Наряду с заочным коллективом корреспондентов существовал и очный кружок—«четверги Мерсенна», в который и попал Блез Паскаль. Здесь он нашел себе достойного учителя. Им был Же-рар Дезарг (1593–1662), инженер и архитектор, создатель оригинальной теории перспективы. Его главное сочетание «Черновой набросок вторжения в область того, что происходит при встрече конуса с плоскостью» (1639 г.) нашло лишь нескольких читателей, и среди них особое место занимает Б. Паскаль, сумевший существенно продвинуться вперед.
Хотя в то время Декарт прокладывал в геометрии совершенно новые пути, создавая аналитическую геометрию, в основном геометрия едва достигла уровня, на котором она находилась в Древней Греции. Многое из наследия греческих геометров оставалось неясным. Это прежде всего относилось к теории конических сечений. Самое выдающееся сочинение на эту тему — 8 книг Аполлония «Konika» — было известно лишь частично. Предпринимались попытки дать модернизированные изложения теории, среди которых наиболее известное принадлежит Клоду Мидоржу (1585 – 1647), члену кружка Мерсенна, но его сочинение фактически не содержало новых идей. Дезарг заметил, что систематическое применение метода перспективы позволяет построить теорию конических сечений с совершенно новых позиций.
Рассмотрим центральную проекцию шестиугольника из некоторой точки O плоскости α на плоскость β (рис. 1). Применять такое преобразование в теории конических сечений очень естественно, поскольку само их определение — как сечений прямого кругового конуса — можно перефразировать так: все они получаются при центральном проектировании из вершины конуса на различные плоскости одного из них (например, окружности). Далее, заметив, что при центральном проектировании пересекающиеся прямые могут перейти или в пересекающиеся или в параллельные, объединим два последних свойства в одно, считая, что все параллельные друг другу прямые пересекаются в одной «бесконечно удаленной точке».
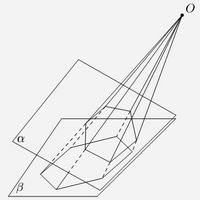
Рис. 1. Проекция шестиугольникаРазные пучки параллельных прямых дают разные бесконечно удаленные точки. Все бесконечно удаленные точки плоскости заполняют «бесконечно удаленную прямую». Если принять эти соглашения, то две любые различные прямые (уже не исключая параллельных) будут пересекаться в единственной точке. Утверждение, что через точку A вне прямой m можно провести единственную прямую, параллельную m, можно переформулировать так: через обычную точку A и бесконечно удаленную точку (отвечающую семейству прямых, параллельных m ) проходит единственная прямая — в результате в новых условиях без всяких ограничений справедливо утверждение, что через две различные точки проходит единственная прямая (бесконечно удаленная, если обе точки бесконечно удалены). Мы видим, что получается очень изящная теория, но для нас важно то, что при центральном проектировании точка пересечения прямых (в обобщенном смысле) переходит в точку пересечения.
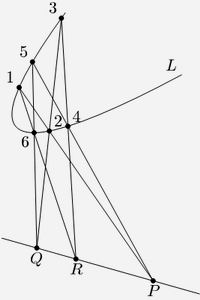
Рис. 2. Чертеж к теореме ПаскаляВ 1640 г. Б. Паскаль напечатал свой «Опыт о конических сечениях». Небезынтересны сведения об этом издании: тираж — 50 экземпляров, 53 строки текста напечатаны на афише, предназначенной для расклейки на углах домов. В афише, подписанной инициалами автора, без доказательства сообщается следующая теорема, которую ныне называют теоремой Паскаля. Пусть на коническом сечении L (парабола) произвольно выбраны и занумерованы 6 точек (рис. 2). Обозначим через P, Q, R точки пересечения трех пар прямых (1,2) и (4, 5); (2, 3) и (5, 6); (3,4) и (6, 1). Тогда точки P, Q, R лежат на одной прямой.
Паскаль вначале формулирует теорему для окружности и ограничивается простейшей нумерацией точек. В этом случае это элементарная, хотя и не слишком простая задача. А вот переход от окружности к любому коническому сечению очень прост. Нужно преобразовать при помощи центральной проекции такое сечение в окружность и воспользоваться тем, что при центральном проектировании прямые переходят в прямые, а точки пересечения (в обобщенном смысле) — в точки пересечения. Тогда, как уже доказано, образы точек P, Q, R при проектировании будут лежать на одной прямой, а отсюда следует, что и сами точки P, Q, R обладают этим свойством.
Теорема, которую Паскаль назвал теоремой о «мистическом шестивершиннике», не была самоцелью; он рассматривал ее как ключ для построения общей теории конических сечений, покрывающей теорию Аполлония. Уже в афише упоминаются обобщения важных теорем Аполлония, которые не удавалось получить Дезаргу. Дезарг высоко оценил теорему Паскаля, назвав ее «великой паскалевой»; он утверждал, что в ней содержатся первые четыре книги Аполлония.
Паскаль начинает работу над «Полным трудом о конических сечениях», который в 1654 г. упоминается как оконченный в послании «знаменитейшей Парижской математической академии». От Мерсенна известно, что Паскаль получил около 400 следствий из своей теоремы. Готфрид Вильгельм Лейбниц (1646 – 1716) был последним, кто видел трактат Паскаля уже после его смерти, в 1675 –1676 гг. Несмотря на совет Лейбница, родные не опубликовали рукопись, а со временем она была утеряна.
2 января 1640 г. семья Паскалей переезжает в Руан, где Этьен Паскаль получает место интенданта провинции, фактически ведающего всеми делами при губернаторе. Этому назначению предшествовали любопытные события. Э.Паскаль принял активное участие в выступлениях парижских рантьеров, за что ему грозило заточение в Бастилию. Он был вынужден скрываться, но в это время заболела оспой Жаклина, и отец, несмотря на страшную угрозу, навещал ее. Жаклина выздоровела и даже участвовала в спектакле, на котором присутствовал кардинал Ришелье. По просьбе юной актрисы кардинал простил ее отца, но одновременно назначил его на должность. Бывший смутьян должен был проводить в жизнь политику кардинала (читателей «Трех мушкетеров» это коварство, наверное, не удивит).
Теперь у Этьена Паскаля было очень много счетной работы, в которой ему постоянно помогает сын. В конце 1640 г. Блезу Паскалю приходит мысль построить машину, чтобы освободить ум от расчетов «с помощью пера и жетонов». Основной замысел возник быстро и оставался неизменным на протяжении всей работы: «...каждое колесо или стержень некоторого разряда, совершая движение на десять арифметических цифр, заставляет двигаться следующее только на одну цифру». Однако блестящая идея — это только первый шаг. Несравненно больших сил потребовала ее реализация. Позднее в «Предуведомлении» тому, кто «будет иметь любознательность видеть арифметическую машину и пользоваться ею», Блез Паскаль скромно пишет: «Я не экономил ни время, ни труд, ни средства, чтобы довести ее до состояния быть тебе полезной». За этими словами стояло пять лет напряженной работы, которая привела к созданию машины («паскалева колеса», как говорили современники), надежно, хотя и довольно медленно, производившей четыре действия над пятизначными числами.
Паскаль изготовил около пятидесяти экземпляров машины; вот только перечень материалов, которые он перепробовал: дерево, слоновая кость, эбеновое дерево, латунь, медь. Он потратил много сил на поиски лучших ремесленников, владеющих «токарным станком, напильником и молотком», и ему много раз казалось, что они не в состоянии достичь необходимой точности. Тщательно продумывается система испытаний, в их число включается перевозка на 250 лье. Паскаль не забывает и о рекламе: он заручается поддержкой канцлера Сегье, добивается «королевских привилегий» (нечто вроде патента), много раз демонстрирует машину в салонах и даже посылает экземпляр шведской королеве Христине. Наконец, налаживается производство; точное число произведенных машин неизвестно, но до настоящего времени сохранилось восемь экземпляров.
В конце 1646 г. до Руана докатилась молва об удивительных «итальянских опытах с пустотой». Вопрос о существовании пустоты в природе волновал еще древних греков. В их взглядах на этот вопрос проявилось присущее древнегреческой философии разнообразие точек зрения. Эпикур считал, что пустота может существовать и действительно существует; Герон — что она может быть получена искусственно, Эмпедокл — что ее нет и ей неоткуда взяться, и, наконец Аристотель утверждал, что «природа боится пустоты». В средние века ситуация упростилась, поскольку истинность учения Аристотеля была установлена практически в законодательном порядке (еще в XVII веке за выступление против Аристотеля во Франции можно было попасть на каторгу).
Классический пример «боязни пустоты» демонстрирует вода, поднимающаяся вслед за поршнем, не давая образоваться пустому пространству. И вдруг с этим примером произошел казус. При сооружении фонтанов во Флоренции обнаружилось, что вода «не желает» подниматься выше 34 футов (10,3 метра). Недоумевающие строители обратились за помощью к престарелому Галилею, который сострил, что, вероятно, природа перестает бояться пустоты на высоте, превышающей 34 фута, но все же предложил разобраться в странном явлении своим ученикам Торричелли и Вивиани.
Вероятно, Торричелли (а, возможно, и самому Галилею) принадлежит мысль, что высота, на которую может подняться жидкость в насосе, обратно пропорциональна ее удельному весу. В частности, ртуть должна подняться на высоту в 13,3 раза меньшую, чем вода, т. е. на 76 . Опыт приобрел масштабы, более благоприятные для лабораторных условий, и был проведен Вивиани по инициативе Торричелли. Этот опыт хорошо известен, но все же напомним, что запаянная с одного конца метровая стеклянная трубка заполняется ртутью, открытый конец зажимается пальцем, после чего трубка переворачивается и опускается в чашку с ртутью. Если отнять палец, то уровень ртути в трубке упадет до 76. Торричелли делает два утверждения: во-первых, пространство над ртутью в трубке пусто (потом его назовут «торричеллиевой пустотой»), а во-вторых, ртуть из трубки не выливается полностью, поскольку этому препятствует столб воздуха, давящий на поверхность ртути в чашке. Приняв эти гипотезы, можно все объяснить, но можно получить объяснение и введя специальные, довольно сложно действующие силы, препятствующие образованию вакуума.
Принять гипотезы Торричелли было непросто. Лишь немногие из его современников смирились с тем, что воздух имеет вес; некоторые, исходя из этого, поверили в возможность получения вакуума, но поверить, что легчайший воздух удерживает в трубке тяжелую ртуть, было почти невозможно. Упомянем, что Галилей пытался объяснить этот эффект свойствами самой жидкости, а Декарт утверждал, что кажущийся вакуум всегда заполнен «тончайшей материей».
Паскаль с увлечением повторяет итальянские опыты, придумав много остроумных усовершенствований. Восемь таких опытов описаны в трактате, опубликованном в 1647 г. Он не ограничивается опытами с ртутью, а экспериментирует с водой, маслом, красным вином, для чего ему потребовались бочки вместо чашек и трубки длиной около 15. Эффектные опыты выносятся на улицы Руана, радуя его жителей.
На первых порах Паскаля более всего интересует вопрос о доказательстве того, что пространство над ртутью пусто. Была распространена точка зрения, что кажущийся вакуум заполняет материя, «не имеющая свойств». Доказать отсутствие такой материи просто невозможно. Четкие высказывания Паскаля очень важны в плане постановки более широкой проблемы о характере доказательств в физике. Он пишет: «После того как я доказал, что ни одна из материй, которые доступны нашим чувствам и которые нам известны, не заполняет это пространство, кажущееся пустым, мое мнение, пока мне не докажут существование какой-то материи, заполняющей его, — что это пространство в самом деле пусто и лишено всякой материи».

Блез Паскаль (1623 – 1662)На родине Паскаля в Клермоне жила в это время старшая сестра Б. Паскаля Жильберта. Ее муж Флорен Перье, служа в суде, свободное время посвящал наукам. 15 ноября 1647 г. Паскаль отправляет Перье письмо, в котором просит сравнить уровни ртути в трубке Торричелли у подножия и на вершине горы Пюи-де-Дом: «Вы понимаете, если бы высота ртути на вершине горы оказалась меньшей, чем у подошвы (я так думаю по многим основаниям, хотя все, писавшие об этом предмете, придерживаются другого мнения), то из этого можно было бы заключить, что единственная причина явления — тяжесть воздуха, а не пресловутая «боязнь пустоты» [horror vacui]. Ясно, в самом деле, что внизу горы воздух должен быть гуще, чем наверху. Нелепо предполагать в нем больший страх пустоты у подножия, нежели на вершине».
Эксперимент по разным причинам откладывался и состоялся лишь 19 сентября 1648 г. в присутствии пяти «уважаемых жителей Клермона». В конце года вышла брошюра, в которую были включены письмо Паскаля и ответ Перье с очень скрупулезным описанием опыта. При высоте горы около 1,5 разница уровней ртути составила 82,5. Это «повергло участников эксперимента в восхищение и удивление» и, вероятно, было неожиданным для Паскаля. Предположить существование предварительных оценок невозможно, а иллюзия легкости воздуха была очень велика.
Результат был столь ощутим, что уже одному из участников эксперимента аббату де ла Мару приходит в голову мысль, что результаты может дать эксперимент в куда более скромных масштабах. И, действительно, разница уровней ртути у основания и наверху собора Нотр-Дам-де-Клермон, имеющего высоту 39, составила 4,5. Если бы Паскаль допускал такую возможность, он не стал бы ожидать десять месяцев. Получив известие от Перье, он повторяет эксперименты на самых высоких зданиях Парижа, получая те же результаты. Паскаль назвал этот эксперимент «великим экспериментом равновесия жидкостей» (это название может вызвать удивление, поскольку речь идет о равновесии воздуха и ртути и тем самым воздух назван жидкостью). В этой истории есть одно запутанное место. Декарт утверждал, что именно он подсказал идею эксперимента. Вероятно, здесь произошло какое-то недоразумение, так как трудно предположить, что Паскаль сознательно не ссылался на Декарта.
Паскаль продолжает экспериментировать, используя наряду с барометрическими трубками большие сифоны (подбирая короткую трубку так, чтобы сифон не работал); он описывает разницу в результатах экспериментов для различных местностей Франции (Париж, Овернь, Дьепп): Паскаль знает, что барометр можно использовать как высотомер (альтиметр), но вместе с тем понимает, что зависимость между уровнем ртути и высотой местности не проста, и обнаружить ее пока не удается. Он замечает, что показания барометра в одной и той же местности зависят от погоды; сегодня предсказание погоды — основная функция барометра (прибор для измерения «изменений воздуха» хотел построить Торричелли). А однажды Паскаль решил вычислить общий вес атмосферного воздуха («мне хотелось доставить себе это удовольствие, и я провел расчет»). Получилось 8,5 триллиона французских фунтов.
Мы не имеем возможности останавливаться на других опытах Паскаля о равновесии жидкостей и газов, поставивших его наряду с Галилеем и Симоном Стевином (1548 –1620) в число создателей классической гидростатики. Здесь и знаменитый закон Паскаля, и идея гидравлического пресса, и существенное развитие принципа возможных перемещений. Одновременно он придумывает, например, зрелищно эффектные опыты, иллюстрирующие открытый Стевином парадоксальный факт, что давление жидкости на дно сосуда зависит не от формы сосуда, а лишь от уровня жидкости: в одном из опытом наглядно видно, что требуется груз в 100 фунтов, чтобы уравновесить давление на дно сосуда воды весом в одну унцию; в процессе опыта вода замораживается, и тогда хватает груза в одну унцию.
Между 29 июля и 27 октября 1654 г. Паскаль обменивается письмами с Ферма. Часто считают, что в этой переписке родилась теория вероятностей. Ферма решает задачу о ставках иначе, чем Паскаль, и первоначально возникают некоторые разногласия. Но в последнем письме Паскаль констатирует: «Наше взаимопонимание полностью восстановлено», и далее: «Как я вижу, истина одна и в Тулузе, и в Париже». Он счастлив тем, что нашел великого единомышленника: «Я и впредь хотел бы по мере возможностей делиться с Вами своими мыслями». В том же 1654 г. Паскаль опубликовал одну из самых популярных своих работ «Трактат об арифметическом треугольнике». Теперь его называют треугольником Паскаля, хотя оказалось, что он был известен еще в Древней Индии, а в XVI веке был переоткрыт Штифелем.
Вскоре после смерти отца (1651 г.) Жаклина Паскаль уходит в монастырь, и Блез Паскаль лишается присутствия очень близкого человека. Какое-то время его привлекает возможность жить, как живет большинство людей: он подумывает о том, чтобы купить должность в суде и жениться. Но этим планам не суждено было сбыться. В середине ноября 1654 г., когда Паскаль переезжал мост, передняя пара лошадей сорвалась, а коляска чудом задержалась у края пропасти. С тех пор, по словам Ламетри, «в обществе или за столом Паскалю всегда была необходима загородка из стульев или сосед слева, чтобы не видеть страшной пропасти, в которую он боялся упасть, хотя знал цену подобным иллюзиям».
23 ноября происходит необычайный нервный припадок. Находясь в состоянии экстаза, Паскаль записывает на клочке бумаги мысли, которые проносятся в его голове: «Бог Авраама, Бог Исаака, Бог Иакова, но не Бог философов и ученых...». Позднее он перенес эту запись на пергамент; после его смерти обе бумаги обнаружили зашитыми в его камзоле. С этого дня, по свидетельству Жаклины, Паскаль чувствует «огромное презрение к свету и почти непреодолимое отвращение ко всем принадлежащим ему вещам». Он прерывает занятия и с начала 1655 г. поселяется в монастыре Пор-Рояль (оплоте янсенистов), добровольно ведя монашеский образ жизни.
В это время Паскаль пишет «Письма к провинциалу» — одно из величайших произведений французской литературы. «Письма» содержали критику иезуитов. Они издавались отдельными выпусками — «письмами», — начиная с 23 января 1656 г. до 23 марта 1657 г. (всего 18 писем). Автора — «друга провинциала» — звали Луи де Монтальтом. Слово «гора» в этом псевдониме (la montagne) уверенно связывают с воспоминаниями об опытах на Пюи-де-Дом. Письма читали по всей Франции, иезуиты были в бешенстве, но не могли достойно ответить. «Делались попытки самыми различными способами показать иезуитов отвратительными; Паскаль сделал больше: он показал их смешными», — так оценивает «Письма» Вольтер. «Шедевром шутливой логики» назвал их Бальзак, «кладом для комедиографа» — Расин. Образы Паскаля предвещали появление мольеровского Тартюфа.
Работая над «Письмами», Паскаль ясно понимал, что правильное владение логикой важно не только математикам. В Пор-Рояле много думали о системе образования, и существовали даже специальные янсенистские «маленькие школы». Паскаль активно включился в эти размышления, сделав, например, интересные замечания о первоначальном обучении грамоте (он считал, что нельзя начинать с изучения алфавита). В 1667 г. посмертно вышли два фрагмента работы Паскаля «Разум геометра и искусство убеждения». Это сочинение не является научной работой; его назначение более скромно — быть введением к учебнику геометрии для янсенистских школ.
«Я провел много времени в изучении отвлеченных наук; недостаток сообщаемых ими сведений отбил у меня охоту к ним. Когда я начал изучение человека, я увидел, что эти отвлечения ему несвойственны и что я еще больше запутался, углубляясь в них, чем другие, не зная их». Эти слова Паскаля характеризуют его настроение в последние годы жизни. И все же полтора года из них он занимался математикой...
Началось это весной 1658 г. как-то ночью, когда во время страшного приступа зубной боли Паскаль вспомнил одну нерешенную задачу Мерсенна про циклоиду. Он замечает, что напряженные размышления отвлекают от боли. К утру он уже доказал целый ряд результатов о циклоиде и... исцелился от зубной боли. Поначалу Паскаль считает случившееся грехом и не собирается записывать полученные результаты. Позднее, под влиянием герцога де Роанне, он изменяет свое решение, в течение восьми дней, по свидетельству Жильберты Перье, «он только и делал, что писал, пока рука могла писать». А затем в июне 1658 г. Паскаль, как это часто делалось тогда, организовал конкурс, предложив крупнейшим математикам решить шесть задач про циклоиду. Наибольших успехов добились Христиан Гюйгенс (1629 – 1695), решивший четыре задачи, и Джон Валлис (1616 – 1703), у которого с некоторыми пробелами были решены все задачи. Но наилучшей была признана работа неизвестного Амоса Деттонвиля. Гюйгенс признавал позднее, что «эта работа выполнена столь тонко, что к ней нельзя ничего добавить».
На этих задачах Паскаль разработал по существу все, что необходимо для построения дифференциального и интегрального исчисления в общем виде. Лейбниц, который делит с Ньютоном славу создателя этой теории, пишет, что когда по совету Гюйгенса он ознакомился с работами Паскаля, его «озарило новым светом», он удивился, насколько был близок Паскаль к построению общей теории и неожиданно остановился, будто «на его глазах была пелена».
Приведем высказывание Н.Бурбаки: «Валлис в 1655 г. и Паскаль в 1658 г. составили каждый для своего употребления языки алгебраического характера, в которых, не записывая ни единой формулы, они дают формулировки, которые можно немедленно, как только будет понят их механизм, записать в формулах интегрального исчисления. Язык Паскаля особенно ясен и точен; и если не всегда понятно, почему он отказался от применения алгебраических обозначений не только Декарта, но и Виета, все же нельзя не восхищаться его мастерством, которое могло проявиться лишь на основе совершенного владения языком».
После середины 1659 г. Паскаль уже не возвращался ни к физике, ни к математике. В конце мая 1660 г. он в последний раз приезжает в родной Клермон; Ферма приглашает его заехать в Тулузу. «Я так слаб, — писал Паскаль 10 августа, — что не могу ни ходить без палки, ни ездить верхом. Я не могу даже ехать в экипаже более двух или трех лье...». В декабре 1660 г. Гюйгенс дважды посетил Паскаля и нашел его глубоким стариком (Паскалю было 37 лет), который не в состоянии вести беседу.
Он растерян: «Я не знаю, кто меня послал в мир, я не знаю, что такое мир, что такое я. Я в ужасном и полнейшем неведении... Как я не знаю, откуда я пришел, так же точно не знаю, куда уйду... Вот мое положение: оно полно ничтожности, слабости, мрака». Его занятия естественными науками не могут помочь ответить на возникшие вопросы: «Знание физики не утешает меня в незнании начал нравственности в момент страданий».
Паскаль много думает о роли религии в жизни человека. Почти нет вопроса, мимо которого он проходит. Он продумывает человеческую историю, подчеркивает роль случая в ней. Его мысли о государстве ценил Наполеон, который, находясь в изгнании на острове св. Елены, говорил, что «сделал бы Паскаля сенатором». Паскаль не окончил главную книгу жизни. Оставшиеся материалы были изданы посмертно в разных вариантах, под разными названиями. Чаще всего книгу называют «Мысли».
Блез Паскаль скончался 19 августа 1662 г. 21 августа в церкви Сент-Этьен-дю-Мон был составлен «Похоронный акт»: «В понедельник 21 августа 1662 г. был похоронен в церкви покойный Блез Паскаль, при жизни стремянный, сын покойного Этьена Паскаля, государственного советника и президента палаты сборов в Клермон-Ферране. 50 священников, получено 20 франков».
Из «Рассказов о физиках и математиках» С.Г. Гиндикина
— М., МЦНМО, НМУ 2001, с. 157 – 179 (с сокращениями)
Б. Паскаль
Трактат о равновесии жидкостей
Глава I. О том, что жидкости имеют вес,
соответствующий высоте их положенияЕсли прикрепить к стене несколько сосудов, один такой, как на фигуре первой, другой наклонный, как на второй, затем более широкий, как на третьей, потом узкий, как на четвертой, затем такой, который представляет собою не что иное как узкую трубку, примыкающую внизу к широкому, но не имеющему почти высоты сосуду, как на фигуре пятой, наполнить их все водой до одинаковой высоты, сделать у всех внизу одинаковые отверстия, каковые закрыть пробками, чтобы удержать воду, то опыт покажет, что нужна одинаковая сила для того, чтобы воспрепятствовать этим пробкам выпасть, хотя вода в этих различных сосудах находится в весьма различных количествах. Происходит это потому, что вода имеет одинаковую высоту во всех сосудах, и мерой указанной силы является вес воды, содержащейся в первом сосуде, однородном по своей форме. И если это количество воды весит сто фунтов, то нужна сила в сто фунтов, чтобы удержать каждую из пробок, даже и у пятого сосуда, хотя вода, заключенная в нем, не весит и одной унции (фиг. I—V).
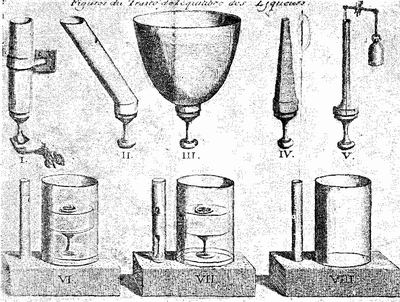
Рис. 1. Рисунки I – VII к трактату Блеза Паскаля "О равновесии жидкостей"Чтобы проверить это точно, надо закрыть отверстие пятого сосуда круглым куском дерева, обернутым прядью, как поршень насоса, каковой кусок должен входить в отверстие и проходить через него с такой точностью, чтобы не застревать и в то же время препятствовать выходу воды, затем прикрепить к середине этого поршня нитку, которая проходила бы через эту тонкую трубку, привязать ее к одному плечу коромысла весов, а на другое плечо повесить груз в сто фунтов. Тогда мы увидим полное равновесие этого груза в сто фунтов с водой в тонкой трубке, каковая вода весит одну унцию. Если же хотя немного уменьшить груз в сто фунтов, то вес воды опустит поршень, а следовательно, и то плечо коромысла весов, к которому он прикреплен, и поднимет то, на котором висит груз немного менее ста фунтов.
Если эта вода замерзнет, и лед, как то в действительности обычно бывает, не пристынет к сосуду, то, чтобы удержать его в равновесии, достаточно будет иметь на другом: плече коромысла весов всего лишь одну унцию. Если же приблизить к сосуду огонь, от которого лед растает, то понадобятся уже сто фунтов, чтобы удержать в равновесии тяжесть этого льда, расплавленного в воду, хотя мы располагаем всего только одной унцией ее.
То же произойдет, если отверстия, которые закрываются пробками, будут сбоку или же в верхней части сосудов. Проверить это будет еще легче следующим образом.
Надо взять сосуд, закрытый со всех сторон, сделать в верхней части его два отверстия, одно очень узкое, другое более широкое, и укрепить над тем и другим трубки такого же размера, как и отверстия. Если вставить теперь в широкую трубку поршень, а в тонкую налить воды, то легко видеть, что на поршень надо будет положить большой груз, чтобы вес воды в тонкой трубке не вытолкнул его вверх, подобно тому как в первых опытах нужна была сила в сто фунтов, чтобы воспрепятствовать выталкиванию поршня вниз, когда отверстие находилось внизу. Если бы отверстие находилось сбоку, то нужна была бы такая же сила, чтобы вес воды не вытолкнул поршень в сторону (фиг. VI).
И если бы трубка, заполненная водой, была во сто раз шире или во сто раз уже, но вода стояла бы во всех случаях на одной высоте, то всегда понадобился бы один и тот же груз, чтобы уравновесить воду. Как только груз этот будет уменьшен, вода опустится и поднимет уменьшенный груз.
Если же налить воду в трубку на двойную высоту, то для уравновешивания воды понадобится действие на поршень двойного груза. Точно так же, если сделать отверстие, в которое вставлен поршень, вдвое большего размера, то надо будет удвоить и силу, необходимую для удержания удвоенного поршня. Отсюда видно, что сила, нужная для того, чтобы воспрепятствовать воде вытекать из отверстия, пропорциональна высоте стояния воды, а не ширине сосуда, и что мерой этой силы всегда является вес воды, заключающейся в колонне ее, с высотой, равной высоте стояния воды, и основанием, равным величине отверстия.
Правило о силе, необходимой для удержания воды То, что я сказал о воде, относится и ко всём другим видам жидкостей.
Глава II. Почему жидкости имеют вес,
соответствующий высоте их положенияИз всех этих примеров видно, что тонкий столбик воды удерживает в равновесии большой груз. Остается показать, какова причина этого увеличения силы. Мы сделаем это на следующем опыте.
Если сосуд, наполненный водою и закрытый со всех сторон, имеет два отверстия, одно во сто раз больше другого, которые прикрыты точно пригнанными к ним поршнями, то один человек, надавливающий на малый поршень, уравновесит силу ста человек, надавливающих на поршень во сто раз больший, и преодолеет силу девяносто девяти (рис. 1, VI).
Новый вид машины для увеличения сил И каково бы ни было отношение этих отверстий, всегда, когда силы, приложенные к поршням, относятся друг к другу, как отверстия, то силы эти будут в равновесии. Отсюда следует, что сосуд, наполненный водою, является новым принципом механики и новой машиной для увеличения сил в желаемой степени, потому что при помощи этого средства человек сможет поднять любую предложенную ему тяжесть.
Надо признать, что в этой новой машине проявляется тот же постоянный закон, который наблюдается и во всех прежних, как то: рычаге, блоке, бесконечном винте и т. д., и который заключается в том, что путь увеличивается в той же пропорции, как и сила. Ибо очевидно, что если одно из этих отверстий во сто раз больше другого, то человек, который давит на малый поршень и опускает его на дюйм, вытолкнет другой поршень лишь на одну сотую часть дюйма.
В самом деле этот толчок происходит вследствие непрерывности воды, соединяющей один поршень с другим и обусловливающей то, что один поршень не может двигаться, не толкая другого. Поэтому, когда малый поршень продвинется на один дюйм, то вода, которую он вытеснил, встретит, толкая другой поршень, отверстие во сто раз большее и займет по высоте лишь сотую часть дюйма. Таким образом, путь относится к пути, как сила к силе. Это можно даже принять за истинную причину указанного явления, так как ясно, что совершенно безразлично, заставить ли сто фунтов воды пройти путь в один дюйм или один фунт воды — путь в сто дюймов. И если фунт воды так связан со ста фунтами ее, что сто фунтов не могут сдвинуться на один дюйм, без того чтобы не передвинуть один фунт на сто дюймов, то они необходимо должны находиться в равновесии, ибо один фунт имеет столько же силы, чтобы заставить сто фунтов сделать путь в один дюйм, сколько сто фунтов для того, чтобы заставить один фунт сделать путь в сто дюймов.
Для еще большего пояснения можно добавить, что вода под этими двумя поршнями сжата одинаково, потому что, если один поршень несет груз в сто раз больший, чем другой, то зато он касается и во сто раз большего числа частиц воды, так что каждый поршень давит одинаково. Следовательно, все частицы должны быть в покое, ибо нет никакого основания, почему бы одна должна была уступать другой. Таким образом, если сосуд, наполненный водой, имеет только одно отверстие, размером, например, в один дюйм, в которое вставлен поршень, нагруженный весом в один фунт, то вес тот (вследствие непрерывности и жидкого состояния воды) оказывает давление вообще на все части сосуда.
Чтобы определить, какое давление испытывает каждая часть, вот правило. Каждая часть, размером, как и отверстие, в один дюйм, подвергается такому же давлению, как если бы на нее действовал груз в один фунт (не считая веса воды, о котором я здесь не говорю, так как я имею в виду только груз на поршне). Почему? Потому что именно этот вес в один фунт давит на поршень, находящийся в отверстии. Каждая часть сосуда, большая или меньшая по размеру, испытывает большее или меньшее давление, соответствующее в точности ее величине, независимо от того, находится ли она против отверстия, сбоку, далеко или близко, потому что непрерывность и жидкое состояние воды уравнивает и делает безразличными эти обстоятельства.
Таким образом, чтобы материал мог выдержать все эти усилия, нужно чтобы сосуд имел во всех своих частях достаточное сопротивление. Если сопротивление какой-нибудь части будет меньше, то она лопнет. Если больше, то она окажет нужное противодействие. Однако излишек прочности в данном случае будет бесполезным.
Точно так же, если в этом сосуде сделать новое отверстие, то, чтобы остановить воду, которая из него польется, необходима будет сила, равная тому сопротивлению, которое эта часть должна оказывать, т.е. сила в один фунт, если это отверстие таково же по величине, как и первое.
Вот еще одно доказательство, которое будет понятно только геометрам и может быть опущено другими.
Я принимаю за принцип, что никогда тело не движется под действием своего веса без того, чтобы центр тяжести его не понижался. Отсюда я вывожу, что два поршня, изображенные на (рис. 1, VII), находятся в равновесии.
Действительно, их общий центр тяжести лежит в точке, которая делит линию, соединяющую их частные центры тяжести, в отношении их весов. Пусть теперь эти поршни, если только это возможно, сдвинутся. При этом их пути будут относиться между собою, как мы уже показали, обратно их весам. Но если отыскать общий центр тяжести их для этого второго положения, то он окажется точно в том же месте, как и в первом случае, потому что он всегда лежит в точке, которая делит линию, соединяющую их частные центры тяжести, в отношении их весов. Таким образом, вследствие параллельности направлений их путей он всегда будет находиться на пересечении двух линий, соединяющих центры тяжести их в двух положениях. Следовательно, общий центр тяжести будет в той же точке, как и прежде, и потому два этих поршня, рассматриваемые как одно тело, должны бы были сдвинуться без понижения их общего центра тяжести. Это, однако, противоречит принципу, и потому они сдвинуться не могут, а должны оставаться в покое, т. е. в равновесии, что и требовалось доказать.
Этим методом я доказал в небольшом Трактате по механике причину всех увеличений сил, которые имеют место во всяких других механических приборах, изобретенных до сего времени. Ибо я нахожу повсюду, что неравные грузы, находящиеся в равновесии и обусловливающие выгодность применения машин, располагаются благодаря самому устройству этих последних таким образом, что общий центр тяжести грузов не может никогда понизиться, какое бы положение они ни занимали. Отсюда следует, что они должны оставаться в покое, т.е. в равновесии.
Итак, примем за несомненную истину, что, если в сосуде, наполненном водой, имеются отверстия, к которым приложены силы, пропорциональные их площадям, то силы эти находятся в равновесии. В этом и состоит основание и смысл равновесия жидкостей, несколько примеров которого мы сейчас приведем.
Этот механический прибор для увеличения сил, если хорошо понять его сущность, выявляет причину, по которой жидкости имеют вес, соответствующий высоте их положения, а не ширине сосудов, во всех случаях, о которых мы говорили выше.
Новый механический прибор позволяет понять, почему жидкости имеют вес, соответствующий высоте их положения Так, на рис. 1, VI видно, что вода в маленькой трубке уравновешивает поршень, нагруженный ста фунтами. Действительно, нижний сосуд является сам по себе сосудом, наполненным водою и имеющим два отверстия. К одному из них примыкает большой поршень, к другому — вода в трубке, являющаяся в сущности таким же поршнем и имеющая собственный вес, который и должен уравновешивать вес другого поршня, если их веса относятся между собою, как площади соответствующих отверстий.
Также и на рис. 1, V вода в тонкой трубке находится в равновесии с грузом в сто фунтов, потому что нижний сосуд, широкий, но небольшой по высоте, является сосудом, закрытым со всех сторон, наполненным водою и имеющим два отверстия, — одно внизу, широкое, где находится поршень, и другое — наверху, узкое, где помещена маленькая трубка. Вода в такой трубке является, собственно говоря, поршнем, имеющим собственный вес и уравновешивающим другой вследствие пропорциональности весов и площадей отверстий, а также того обстоятельства, что, как уже указывалось выше, совершенно безразлично, расположены ли эти отверстия друг против друга или нет.
Отсюда видно, что вода в этих трубках играет ту же роль, как и медные поршни того же веса, ибо медный поршень, весящий одну унцию, будет точно так же находиться в равновесии с грузом в сто фунтов, как и маленький столбик воды, весящий одну унцию.
Таким образом причина того явления, что небольшой груз уравновешивает груз более тяжелый, которое наблюдается во всех этих примерах, лежит не в том, что тела, которые весят так мало и которые уравновешивают гораздо более тяжелые, сами состоят из жидкого вещества. Действительно, это не было непременным условием во всех опытах, потому что и там, где маленькие медные поршни уравновешивали более тяжелые, оказывалось то же самое. Причина состоит в том, что вещество, которое содержится в сосудах и заполняет их от одного отверстия до другого — жидкое, только это обстоятельство является общим для всех примеров. Это и есть истинная причина такого увеличения силы.
Аналогично, если в примере на рис. 1, V, вода, находящаяся в маленькой трубке, замерзнет, а вода, находящаяся в широком нижнем сосуде, останется жидкой, то понадобятся сто фунтов, чтобы удержать вес этого льда. Если же замерзнет вода, находящаяся в нижнем сосуде, то независимо от того, замерзнет ли вода в другом сосуде или останется жидкой, понадобится только одна унция, чтобы уравновесить ее.
Отсюда становится ясным, что жидкое состояние тела, простирающегося от одного отверстия до другого, является причиной увеличения сил. Это и есть основание тому, что, как мы уже говорили, сосуд, наполненный водой, представляет собою механический прибор для увеличения сил.
Перейдем к другим явлениям, причину которых открывает нам эта машина.
Глава III. Пример и причины равновесия жидкостей
Пусть сосуд, наполненный водой, имеет два отверстия, к каждому из которых приделана трубка. Если в последние налить воды до одинаковой высоты, то оба столба жидкости будут в равновесии (фиг. VIII). Так как высоты столбов жидкости одинаковы, то веса их будут относиться между собою, как их толщины, т.е. как площади отверстий. Объемы воды, находящейся в этих трубках, явятся как бы двумя поршнями, веса которых пропорциональны площадям отверстий. Вот почему, согласно предыдущим доказательствам, оба столба воды и будут в равновесии.
Отсюда следует, что, если наливать воду только в одну из этих трубок, то она будет поднимать воду в другой, до тех пор пока та не достигнет одинаковой с ней высоты. После этого оба столба жидкости останутся в равновесии, потому что это будут два поршня, имеющие веса, пропорциональные площадям отверстий. Это есть причина, по которой вода поднимается так же высоко, как ее источник.
Почему вода поднимается так же высоко, как и ее источник Если в трубки налить различные жидкости, например воду в одну и ртуть в другую, то обе эти жидкости придут в равновесие, когда их высоты станут пропорциональны их весам, т.е. когда высота столба воды будет в четырнадцать раз больше высоты столба ртути, потому что ртуть сама весит в четырнадцать раз больше, чем вода. Это будут два поршня, один из воды, а другой из ртути, веса которых пропорциональны площадям отверстий.
И даже если трубка с водой будет во сто раз тоньше, чем та, где находится ртуть, то этот маленький столбик воды удержит в равновесии всю большую массу ртути, лишь бы он был в четырнадцать раз больше по высоте.
Эти опыты можно производить, лишь наполняя сосуд до отверстия трубок жидкостью, более тяжелой Все, что мы говорили до сих пор о цилиндрических трубках, нужно распространить и на сосуды, каковы бы правильной или не правильной формы они ни были, потому что здесь имеет место то же самое равновесие.
Так что, если вместо тех двух трубок, которые мы представляли себе примкнутыми к отверстиям, приставить к последним два так же плотно примыкающих сосуда, которые будут в некоторых местах широкими, в других узкими или наконец совсем неправильными по форме, и наполнить их жидкостями до указанной нами высоты, то последние будут находиться в равновесии и в этих неправильных трубках, точно так же, как и в правильных. Причина этому та, что давление жид остей соответствует только высоте их положения, но не ширине сосудов.
Доказать это очень легко, вписав в тот и другой сосуд несколько маленьких правильных трубок. Тогда на основании только что доказанного будет видно, что две из этих вписанных трубок, соответствующие одна другой в обоих сосудах, находятся в равновесии. Все трубки одного сосуда будут в равновесии со всеми трубками другого. Те, кто привык к геометрическим описаниям, поймут это без малейшего затруднения; другим же, менее сведущим, доказать это будет трудно, по крайней мере геометрическим путем.
Если опустить в реку трубку с загнутым нижним концом, наполненную ртутью, таким образом, чтобы верхний конец ее выступал из воды, то ртуть частично выльется и уровень ее понизится до некоторой высоты. Далее уровень ее понижаться уже не будет и останется в таком положении, при котором высота ртути будет составлять четырнадцатую часть высоты воды над загнутым концом. Таким образом, если высота воды над загнутым концом составляет четырнадцать футов, то уровень ртути будет падать до тех пор, пока не достигнет высоты всего в один фут над загнутым концом, на каковой высоте он и остановится. Вес ртути, действующий внутри, будет уравновешиваться весом воды, действующим снаружи трубки, потому что эти жидкости имеют высоты стояния, пропорциональные их весам, ширина же их для равновесия — безразлична. По той же причине совершенно безразлично, будет ли загнутый конец широким или узким, равно как мало или много воды давит на него (рис. 2, IX).
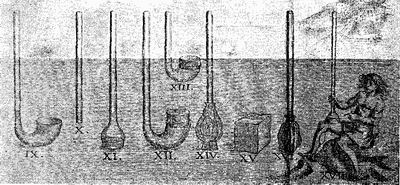
Рис. 2. Рисунки IX – XVII к трактату Блеза Паскаля "О равновесии жидкостей"Точно так же, если опускать трубку глубже, то ртуть поднимается, потому что вес воды становится большим, и наоборот, если ее поднимать, то ртуть падает, так как вес ее превышает вес воды. Если трубку наклонять, то ртуть поднимается, до тех пор пока не достигнет необходимой высоты, уменьшенной наклонением трубки, ибо наклоненная трубка не имеет той высоты, как стоящая отвесно.
То же самое происходит в обыкновенной трубке, т. е. не загнутой. Если такую трубку, открытую сверху и снизу, наполнить ртутью и опустить в реку так, чтобы верхний конец ее выступал из воды, а нижний отстоял от уровня воды на четырнадцать футов, то ртуть будет вытекать, до тех пор пока высота ее не станет равной, одному футу. Так она останется висеть под действием веса воды. Почему это происходит, легко понять.
Действительно, вода, касаясь ртути снизу, а не сверху, стремится вытолкнуть ее вверху, как поршень, причем это усилие тем больше, чем больше высота воды. Так как вес этой ртути имеет столько же силы, чтобы упасть, сколько вода, чтобы вытолкнуть ее кверху, то все и остается уравновешенным (рис. 2, X).
Если бы в трубке не было ртути, то ясно, что вода вошла бы в нее и поднялась на высоту четырнадцати футов, т.е. до уровня ее в реке. Но так как фут ртути весит столько же, сколько эти четырнадцать футов воды, место которых фут занял, то, естественно, что он держит воду в таком же равновесии, как держали его эти четырнадцать футов воды. Если же опустить трубку в воду настолько, что верхний конец се погрузится, то вода войдет в трубку, и ртуть вытечет. Так как вода весит столько же внутри, как и снаружи трубки, то ртуть останется без необходимого для ее удержания противовеса.
Глава IV. О равновесии жидкости и твердого тела
Теперь мы дадим примеры равновесия воды и массивных тел, например, медного массивного цилиндра. Его можно заставить плавать в воде следующим образом.
Надо взять очень длинную трубку, например, в двадцать футов, которая расширялась бы к нижнему концу, наподобие так называемой воронки. Этот нижний конец должен быть круглым. В него надо вставить медный цилиндр, обточенный с такой точностью, чтобы он мог входить и выходить в отверстие этой воронки и перемещаться в ней, но так, чтобы вода не могла проходить между ним и стенками воронки. Таким образом, он будет служить поршнем.
Опуская цилиндр вместе с воронкой в реку так, чтобы конец трубки выступал из воды, держа трубку в руке и предоставляя медный цилиндр самому себе, мы увидим, что этот массивный цилиндр не падает. Он остается подвешенным, так как вода касается его снизу, а не сверху. Она не может войти в трубку. Таким образом, вода толкает его вверху так же, как в предыдущем примере она толкала ртуть, и притом с такой же силой, с какой медный груз стремится упасть. Оба эти противоположные усилия уравновешиваются.
Правда, для достижения такого эффекта нужно, чтобы груз был глубоко в воде, чтобы последняя имела необходимую для уравновешивания меди высоту. Если, например, цилиндр имеет высоту в один фут, то нужно, чтобы от уровня воды до основания цилиндра было девять футов, поскольку медь сама по себе весит в девять раз больше воды. Если же вода не будет иметь достаточной высоты — это произойдет, например, если вынимать трубку из воды — то вес таковой уменьшится, и цилиндр упадет. Если, наоборот, опустить трубку глубже, чем следует, например на двадцать футов, то не только цилиндр не сможет упасть под действием своего веса, но понадобится еще употребить большое усилие, чтобы его отделить и извлечь из воронки, так как вес воды толкает его кверху с силой, соответствующей высоте ее в двадцать футов. Если же пробить трубку, то вода войдет в нее и будет давить на цилиндр одинаково как сверху, так и снизу. Тогда под действием своего веса он упадет, как и ртуть в другом примере, так как не будет больше противовеса, который бы его поддерживал (рис. 2, XI).
Глава V. О телах, которые полностью погружены в воду
Мы видели выше, что вода выталкивает кверху тела, которых она касается снизу; она толкает книзу те тела, которых касается сверху; и она толкает в сторону те тела, которых касается с противоположной стороны. Отсюда легко заключить, что когда тело полностью погружено в воду, то вода, касающаяся его сверху, снизу и со всех сторон, стремится толкать его и кверху, и книзу, и во все стороны. Но так как высота воды является мерилом той силы, которую она проявляет во всех этих давлениях, то очень легко видеть, какое из этих усилий должно преобладать.
Так как вода имеет одинаковую высоту по отношению ко всем боковым поверхностям тела, то она давит на них одинаково. Поэтому это тело не получит никакого сдвига ни в одну из сторон. Оно будет подобно флюгеру, находящемуся под действием двух, одинаковых ветров. Но так как вода имеет большую высоту по отношению к нижней поверхности тела, чем к верхней, то ясно, что она будет больше толкать его вверх, чем вниз. А так как разность этих высот воды равна высоте самого тела, то легко понять, что вода будет толкать его больше кверху, чем книзу, и при том с силой, равной весу объема воды, занимаемого телом (рис. 2, XV).
Таким образом тело, погруженное в воду, поддерживается такой же силой, как если бы оно находилось на одной чашке весов, другая чашка которых нагружена объемом воды, равным объему тела. Отсюда ясно, что если тело сделано из меди или из иного вещества, которое весит больше, чем вода в том же объеме, то оно тонет, потому что вес его превосходит тот, который его уравновешивает. Если тело сделано из дерева или другого вещества, более легкого, чем вода в том же объеме, то оно поднимается в ней со всей той силой, на которую вес воды превосходит, вес тела. Если же оно весит столько же, сколько и вода, то оно не тонет и не всплывает, как воск, который держится в воде приблизительно около того места, куда его опустили.
Тело, находящееся в воде, уравновешивается равным объемом воды Отсюда следует, что ведро из колодца нетрудно поднимать, пока оно находится в воде, и что вес его ощущается только тогда, когда оно начинает из нее выходить. Равным образом и ведро, полное воска, нетрудно было бы поднимать, пока оно находится в воде. Это не значит, что вода, равно как и воск, имеет в воде иной вес, нежели в воздухе. Это только указывает, что, находясь в воде, они имеют противовес, который они теряют, будучи вынутыми из нее. Подобным же образом нетрудно поднять одну чашку весов, нагруженную ста фунтами, если другая весит столько же.
Далее ясно, что если медь погружена в воду, то она весит меньше на вес равного ей объема воды. Если в воздухе она весит девять фунтов, то в воде она весит только восемь, ибо вода в том же объеме, создающая противовес, весит один фунт. В морской же воде медь будет весить еще меньше, потому что морская вода весит больше приблизительно на одну сорок пятую часть.
По той же причине, если два тела, одно из меди, другое из свинца, равного веса и следовательно разного объема (меди для того же веса требуется большее количество) положить на чашки весов, то они будут в равновесии. Но если весы эти опустить в воду, то тела не будут уже больше находиться в равновесии, потому что каждое из них встретит противовес объема воды, равного его собственному объему. А так как объем меди больше, чем объем свинца, то первый будет иметь больший противовес, и потому вес свинца перетянет.
Точно так же пусть два груза из разного материала приведены в полное равновесие с предельной степенью точности, которую только люди могут достичь. Если они находятся в равновесии, когда воздух очень сух, то они потеряют его, когда воздух станет сырым.
По той же причине, когда человек находится в воде, то вес ее вовсе не толкает его книзу; наоборот, он толкает его кверху. Но человек весит больше, чем вода, а потому он опускается в воде, хотя с гораздо меньшей скоростью, чем в воздухе, так как этому противодействует равный ему объем воды, который весит почти столько же, сколько он сам. Если бы человек весил ровно столько же, сколько вода, то он бы плавал. Поэтому, отталкиваясь от земли или делая малейшее усилие против воды, человек поднимается и плавает. В грязевые ванны человек вовсе не может погрузиться. Если же его туда погружают, то он поднимается сам по себе.
Равным образом, когда мы купаемся в ванне, нам не составляет никакого труда поднять руку, пока она находится в воде. Но когда мы вынем ее оттуда, то почувствуем, что она весит много, потому что она более не имеет того противовеса в виде равного объема воды, который был у нее, пока она находилась в воде.
Наконец, тела, которые плавают на воде, весят как раз столько, сколько и вода, место которой они занимают, потому что вода, касаясь их снизу, а не сверху, толкает их только вверх. Вот почему свинцовая пластинка, имеющая выпуклую форму, плавает. Благодаря своей форме она занимает в воде большее место по сравнению с тем, которое она заняла бы, будучи массивной. В последнем случае она заняла бы в воде место, равное объему материала, из которого она сделана, а этого было бы недостаточно, для того чтобы ее уравновесить.
Глава VI. О сжимаемых телах, находящихся в воде
Из всего того, что я изложил, видно, каким образом вода действует на все находящиеся в ней тела, давя на них со всех сторон. Отсюда легко вывести, что если в воду будет погружено сжимаемое тело, то она должна будет сжать его по направлению к центру. И она это сделает, как это будет видно из следующих примеров.
Если мехи, имеющие довольно длинную трубку, например в двадцать футов, опущены в воду так, что конец трубки выступает из нее, а маленькие отверстия с одной стороны мехов заткнуты, то открыть эти мехи в воде будет трудно, тогда как в воздухе они открываются без труда. Происходит это потому, что вода сжимает мехи со всех сторон. Если же применить всю необходимую силу и открыть мехи, то как только сила эта ослабнет, они стремительно захлопнутся (вместо того, чтобы оставаться открытыми, как это было бы в воздухе) по причине действия веса массы воды, который на них давит. И чем глубже погружены мехи, тем труднее их открыть, потому что надо преодолевать большую высоту воды (рис. 2, XIV).
Точно так же, если вставить трубку, длиной в двадцать футов, в отверстие мешка, обвязать мешок кругом конца этой трубки, налить в нее ртути, до тех пор пока мешок не наполнится ею, и опустить все это в чан с водой так, чтобы конец трубки выступал из воды, то можно будет заметить, что ртуть поднимется в трубке на некоторую высоту. Происходит это по той причине, что вес воды давит на мешок со всех сторон. Вследствие этого и ртуть, заключающаяся в нем, испытывает давление, одинаковое во всех точках, за исключением тех, которые лежат в месте входа трубки (потому что вода не имеет туда доступа, ибо трубка, выступающая из воды, препятствует этому) и выталкивается с тех мест, где она испытывает давление по направлению к тем, где его нет. Таким образом, она поднимается в трубке до той высоты, на которой она весит столько же, сколько и вода снаружи трубки (рис. 2, XVI).
Здесь происходит то же самое, как если бы сжимать мешок руками. Тогда можно без труда заставить жидкость, заключающуюся в нем, подняться в трубке. Понятно, что вода, окружающая мешок, давит на него точно таким же образом.
По той же причине, если человек поставит себе на колено конец стеклянной трубки, длиной в двадцать футов, и погрузится в таком положении в чан, полный воды, причем верхний конец трубки будет выступать из воды, то тело его вздуется в том месте, которое находится у отверстия трубки, и там образуется большая опухоль, причиняющая боль, как будто на тело поставлена кровососная банка.
Происходит это потому, что вес воды сжимает его тело со всех сторон за исключением той части, которая находится у отверстия трубки, и которой вода не может достигнуть, так как трубка препятствует входу ее туда. Тело как бы сдвигается с тех мест, где оно подвергается давлению, к тому месту, где такового нет. Чем больше высота воды, тем больше эта вздутие. Если воду удалить, то вздутие пропадет. То же произойдет, если налить в трубку воды, потому что вес ее будет действовать на эту часть так же, как и на другие, и в этом месте не должно образоваться вздутия (рис. 2, XVII).
Явление это вполне сходно с предыдущим, так как в одном случае ртуть, а в другом — тело человека, будучи сжаты во всех своих частях за исключением тех, которые находятся у отверстий трубок, вталкиваются в эти последние, поскольку сила веса воды может это сделать.
Если на дно сосуда с водой поместить мешок, в котором находится не очень сильно сжатый воздух, то можно видеть, что он заметно сжимается. По мере же того как мы будем отливать воду, мешок будет постепенно расширяться, так как вес массы воды, находящейся над ним, сжимает его со всех сторон к центру, до тех пор пока упругость этого сжатого воздуха не делается равной весу сжимающей его воды.
Если на дно того же сосуда с водой поместить мешок, наполненный сильно сжатым воздухом, то не будет заметно никакого сжатия. Это не значит однако, что вода его не сжимает, так как противоположное наблюдается с другим мешком, с мешком, где была ртуть, с мехами и во всех других примерах. Это значит только, что вода не имеет силы заметно сжать воздух, потому что он уже и без того очень сжат. То же мы имеем в сильно натянутой пружине, например в арбалете, которую нельзя уже заметно согнуть умеренной силой, тогда как более слабая пружина сжимается ею очень заметно.
И не следует удивляться тому, что вес воды не сжимает заметно мешка, в то время как его можно гораздо заметнее сжать, надавливая на него сверху пальцем, хотя сжимающая сила будет в этом случае меньше той, с которой давит вода. Причина этой разницы заключается в том, что когда мешок находится в воде, то она давит на него со всех сторон, тогда как при нажатии на него пальцем он подвергается давлению только в одной части; а когда на него давят только в одном месте, то в нем без труда получается большое углубление, так как соседние части не сжаты, и среди них легко распределяется то, что удаляется из части, подверженной давлению. Таким образом материя, удаляемая давлением в одном месте, распределяется по всем остальным, и каждое из них получает ее понемногу; благодаря этому в данном месте образуется углубление, которое становится очень заметным по сравнению со всеми окружающими его частями, не имеющими такового.
Если же начать давить на все другие части с той же силой, как и на первую, то каждая из них отдаст то, что получила от первой, и возвратится в свое первоначальное состояние, потому что все они будут сами сжаты так же, как и она. И так как теперь будет иметь место лишь одно общее сжатие всех частей по направлению к центру, то нигде не будет более заметно местного сжатия, и судить об этом общем сжатии можно будет лишь сравнивая объем, занимаемый мешком, с тем, который он занимал ранее. А так как объемы эти очень мало обличаются друг от друга, то разницу эту заметить невозможно. Отсюда видно, каково различие между давлением в одном только месте и общим сжатием всех частей.
Это имеет сходство с телом, у которого сжаты все части за исключением только одной, где образуется вздутие вследствие притока вещества из других частей, как было показано на примере человека в воде с трубной на колене (рис. 2, XVII). Точно так же, если мы начнем сжимать тот же мешок руками, то хотя бы мы и старались касаться каждой его части, всегда какая-нибудь из них останется между пальцами, и здесь образуется большое вздутие. Но если бы можно было произвести давление, распределенное повсюду равномерно, то мешок никогда нельзя было бы сжать заметно, какое бы усилие ни употреблять, при условии, что воздух в нем уже достаточно сильно сжат сам по себе. Это происходит, когда он находится в воде, потому что она объемлет его со всех сторон.
Глава VII. О животных, которые находятся в воде
Все это объясняет нам, почему вода совсем на сжимает животных, находящихся в ней, хотя вообще она и оказывает давление на все тела, окруженные ею, как мы уже показали это на стольких примерах. Это не значит, что она не давит на животных, но, как мы уже говорили, она, касаясь их со всех сторон, не может вызвать ни вздутия, ни углубления в каком-либо отдельном месте, а производит только общее сжатие всех частей к центру, которое не может быть заметно, если оно невелико, и которое может быть лишь чрезвычайно слабым по причине того, что тело животных очень плотно.
Если бы она касалась только одного места тела или же всех, за исключением одного, то при условии значительной высоты действие ее было бы заметно, как это мы уже видели выше. Но так как она давит на тело повсюду, то ничего и не проявляется. Отсюда легко перейти к причине, по которой животные, находящиеся в воде, не чувствуют ее веса.
Действительно боль, которую мы чувствуем, когда что-нибудь давит нас, велика, если давление велико, потому что сжатая часть обескровливается, и мясо, нервы и другие части, составляющие ее, сдвигаются с их естественного места, а такое насилие не может происходить без боли. Но если давление невелико, например, когда касаются пальцем кожи так легко, что та часть, до которой дотрагиваются, не обескровливается, ее мясо и нервы не страгиваются с места, и вообще не происходит никакого изменения, то не должно испытываться и чувствительной боли. Если же нас касаются таким образом во всех точках тела, то мы не должны чувствовать от подобного легкого давления никакой боли.
Именно это и происходит с животными, находящимися в воде. Вес ее в действительности оказывает на них давление, но такое малое, что оно ни в каком случае не ощущается, по только что рассмотренной причине. В самом деле, так как ни одна часть тела их не сжата, не обескровлена, ни один нерв, вена или мясо не сдвинуты с места — коль скоро все находится под одинаковым давлением — то нет причины, почему они должны сдвинуться к какому-нибудь одному месту, а не к другому, т.е. все остается без изменения, то, следовательно, тело не должно испытывать ощущения боли.
Пусть не удивляются тому, что животные не ощущают вовсе веса воды, но тем не менее чувствуют, если на них нажать сверху пальцем, хотя в этом случае нажим происходит с меньшей силой, чем это делает вода. Причина этой разницы в том, что, находясь в воде, они сжаты ею вообще со всех сторон, тогда как при нажиме на них пальцем они подвергаются давлению только в одной какой-нибудь части. Мы показали, что эта разница и есть причина, вследствие которой можно произвести заметное сжатие прикосновением конца пальца, тогда как вес воды не производит заметного сжатия, хотя бы он и был больше во сто раз. Так как ощущение всегда пропорционально давлению, то эта же разница и является причиной того, что животные чувствуют прикосновение нажимающего на них пальца, но не вес воды.
Итак, истинная причина, которая обусловливает, что животные в воде не ощущают веса ее, состоит в том, что они сжаты со всех сторон одинаково.
Точно так же, если заключить червяка в тесто и мять последнее в руках, то червяка никогда нельзя ни раздавить, ни повредить, ни даже сжать, потому что он будет подвергаться давлению во всех точках. Следующий опыт подтвердит это.
Надо взять стеклянную трубку, заткнутую снизу и налитую до половины водой, бросить туда три вещи: небольшой мешок, надутый до половины воздухом, еще один мешок, надутый полностью, и муху, которая в теплой воде живет так же хорошо, как и в воздухе. Далее нужно вставить в эту трубку поршень, доходящий до воды. Если нажимать на этот поршень с некоторой силой, например накладывая на него в большом количестве грузы, то произойдет следующее. Сжатая вода будет давить на все, что в ней находится. При этом мягкий мешок сожмется очень заметно, а твердый не будет сжат вовсе, как если бы на него ничего не давило. То же самое будет и с мухой. Она не будет испытывать никакой боли под действием этого большого веса, и можно будет видеть, что она свободно и быстро прогуливается вдоль стекла и даже улетает, будучи освобожденной из этой тюрьмы.
Не надо иметь много знаний, чтобы извлечь из этого опыта выводы, совпадающие с ранее доказанным. В самом деле ясно, что этот вес давит, поскольку он может, на все тела. Ясно, что он сжимает мягкий мешок. Следовательно, он давит также и на тот, который находится рядом, потому что та же причина действует как в одном, так и в другом случае. Но из опыта видно, что на последнем не проявляется никакого сжатия.
Отчего же происходит эта разница, и откуда она может получиться, как не от того единственного обстоятельства, которым мешки отличаются друг от друга. Причина состоит в том, что один мешок весь наполнен сжатым воздухом, закаченным туда с силой, тогда как другой мешок наполнен лишь наполовину. Таким образом, слабый воздух, содержащийся в одном из мешков, способен к сильному сжатию; другой же не способен, потому что он очень плотен, и сжимающая его вода, окружая его со всех сторон, не может произвести чувствительного сжатия, потому что она давит как бы на образующиеся со всех сторон своды.
Очевидно также, что и животное совсем не сжато. Почему? — Да по той же причине, по которой не сжат мешок, сполна заполненный воздухом. И наконец ясно, что животное по той же причине не испытывает никакой боли.
Если поместить на дно той же трубки вместо воды тесто, а в него мешок и ту же муху, сверху же наложить поршень, то, нажимая на него, мы увидим, что произойдет то же самое.
А так как соблюдение условия быть сжатым со всех сторон приводит к тому, что сжатие не может ни ощущаться, ни быть болезненным, то не следует ли согласиться с тем, что это и есть единственная причина того, что вес воды делается неощутимым для животных, находящихся в ней?
Пусть не говорят более, что это потому, что вода невесома сама по себе, ибо она весит повсюду одинаково; или что вес ее отличается от веса твердых тел, ибо всякий вес по природе своей одинаков. Мы имеем уже пример, когда муха переносит вес твердого тела, не ощущая его.
И если мы пожелаем иметь еще что-либо более доказательное, то вынем поршень и нальем в трубку воды, до тех пор пока вода, заменяющая поршень, не будет весить столько же, сколько и сам поршень. Нет сомнения, что муха так же не почувствует веса этой воды, как и веса поршня.
Откуда, однако, происходит эта нечувствительность под таким большим весом в этих двух примерах? Не оттого ли, что вес этот состоит из воды? Нет, ибо когда вес вызывается плотным телом, происходит то же самое. Признаем же, наконец, что это происходит единственно потому, что животное окружено водой, так как только это обстоятельство является общим в обоих примерах. Таким образом, в этом и заключается истинная причина явления.
Точно так же, если случится, что вода, находящаяся над этим животным, замерзнет, но так, что над ним останется немного жидкости, и оно будет вполне окружено ею, то и тогда животное не почувствует веса этого льда, как прежде веса воды.
Но если вся вода в реке замерзнет за исключением слоя в один фут над дном, то рыбы, которые там плавают, так же не будут чувствовать веса этого льда, как и веса воды, в которую он потом обратится.
Итак животные в воде не чувствуют ее веса не потому, что давление сверху производится водою, а потому, что они кружены водой.
Из книги: «Классики физико-математических наук: Архимед, Стэвин, Галилей, Паскаль». — М.-Л., Государственное технико-теоретическое издательство, 1932. с. 234 – 260
Из примечания к Трактату
А.Н. ДолговЭтот трактат издан в 1663 году, т. е. через год после смерти автора, вместе с работой, посвященной давлению воздуха. Трактаты о равновесии жидкостей и весе массы воздуха написаны Паскалем в 1651—1653 гг., причем основные положения первого трактата используются во втором. Оба трактата сопровождаются и общим заключением, которое касается, однако, лишь вопросов о давлении воздуха.
Трактат о весе массы воздуха подводит итоги длительным работам Паскаля по изучению атмосферного давления, начатым им в 1644 г., когда до него впервые дошли сведения об опыте Торичелли. Первые результаты своих исследований в этом направлении он опубликовал в Париже в 1647 году. По просьбе Паскаля в сентябре 1648 г. Флореном Перье были произведены известные наблюдения над изменением барометрического давления при восхождении на гору Пюи-де-Дом в Оверне. Постепенно интерес Паскаля к физическим опытам падал. С 1653 года он прекратил экспериментировать.
Полный перевод помещаемого здесь трактата о равновесии жидкостей был выполнен покойным инженером В.Н. Степановым и обработан мною. Вследствие чрезвычайной ясности изложения текст этого трактата Паскаля совершенно не нуждается в каких-либо пояснительных замечаниях.
Математический вывод закона Паскаля
Плотность, вязкость и другие характеристики жидкости рассмотрены в отдельном разделе — Свойства жидкости. Здесь мы проанализируем два самых элементарных закона гидростатики, которые вводится через понятие гидростатического давления. С этой целью рассмотрим некоторый объем покоящейся жидкости (рис. 3, слева). Рассечем его горизонтальной поверхностью abcd на две не обязательно равные части и мысленно отбросим одну из них, например верхнюю (рис. 3, справа). Хотя с таким же успехом мы могли бы отбросить и нижнюю часть — дальнейшие рассуждения от этого не изменятся. Мы должны приложить ко всей поверхности abcd силы, действие которых будет эквивалентно взаимодействию отброшенной и оставшейся частей объема.
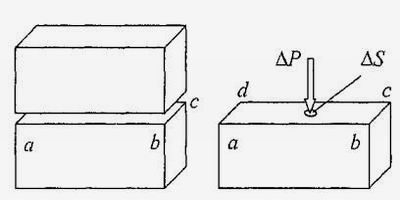
Рис. 3. Чертеж к определению гидростатического давленияТеперь выделим на поверхности abcd замкнутый контур площадью ΔS . Обозначим силу взаимодействия между слоями жидкости, приходящуюся на ΔS, через ΔP. Отношение ΔP / ΔS определяет некоторое усредненное значение давления на выделенной площадке. Если конечную площадку ΔS стянуть в точку, то получим истинное значение гидростатического давления в данной точке:
.
Гидростатическое давление действует по нормали к площадке и является сжимающим, т.е. направлено внутрь того объема жидкости, давление на который рассматривается. Величина гидростатического давления в данной точке не зависит от угла наклона или направления действия силы ΔP, а только от положения точки в объеме жидкости. Для доказательства последнего положения вычертим рис. 4, на котором представлена уже наклоненная поверхность abc.
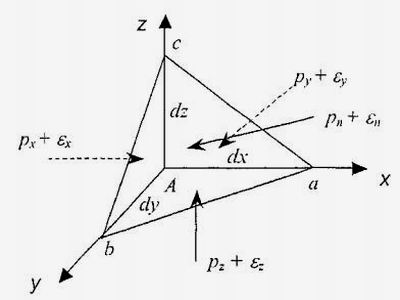
Рис. 4. Силы, действующие на площадку произвольного положения в покоящейся жидкостиВ окрестности точки A из-за наличия земной гравитации на весть внутренний объем тетраэдр с ребрами dx, dy, dz действуют сила, приложенные к каждой точке жидкости. Обозначим через px , py , pz три составляющие силы, действующие перпендикулярно с внешней стороны на три грани тетраэдра — aAc, cAb, aAb. Четвертую компоненту обозначим как pn ; она действует на грань abc тоже с внешней стороны. Очевидно, что в окрестности точки A средние напряжения для четырех граней тетраэдра отличаются от истинных величин гидростатических давлений непосредственно в точке A бесконечно малыми приращениями — εx , εy , εz .
Составим условие равновесия всех вышеперечисленных сил. Прежде всего определим сумму их проекций на ось x. Давления на грани cAb и aAb имеют проекции на ось x, равные нулю. Давление на грань aAc дает проекцию
.
Проектируя на ось x давление, действующее на наклонную плоскость abc, получим выражение
,
где dω — площадь грани abc, n — внешняя нормаль.
Проекция объемных сил равна массе выделенного тетраэдра, умноженной на величину массовой силы X:
.
Так как проекция этих сил на ось x при равновесии равна нулю, то
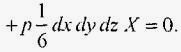
Проанализируем это уравнение. Два первых компонента имеют бесконечно малые второго порядка (dydz и dω); третий компонент dxdydz — бесконечно малая третьего порядка; поэтому в пределе он исчезнет. Кроме того, из чертежа (рис. 4) следует, что
.
Таким образом, уравнение баланса сил упрощается до выражения
.
При уменьшении размеров тетраэдра в пределе до нуля, правая часть устремится тоже к нулю, поэтому px = pn . Аналогичные рассуждения строятся относительно осей y и z, так что в итоге получим px = py = pz = pn . Другими словами, точка A испытывает одинаковое давление со всех сторон. Этим строго математическим путем мы доказали эмпирический закон, открытый еще Блезом Паскалем (1623 – 1662). Закон Паскаля гласит: давление, производимое на жидкость, передается внутри нее во все стороны с одинаковой силой.
Закон Архимеда
В пятой главе «Трактата о равновесии жидкостей», которая называется «О телах, полностью погруженных в воду», Паскаль подробно остановился на гидростатическом законе, открытом еще Архимедом. В наиболее лаконичной формулировке Паскаля закон Архимеда, имя которого он, впрочем, не назвал, звучит так: тела, плавающие на воде, весят ровно столько, сколько и вода, занятая ими. Рассмотрим некоторое тело, погруженное в воду (рис. 5).
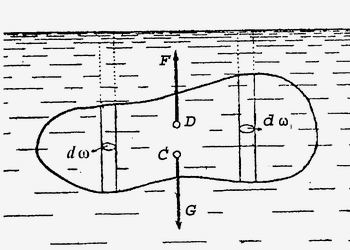
Рис. 5. К выводу закона АрхимедаЕсли разбить все это тело на ряд элементарных цилиндров с поперечным сечением dω , то нетрудно убедиться в том, что на каждый из таких цилиндров действует подъемная сила dF, равная весу жидкости в объеме цилиндра. Равнодействующая этих элементарных сил равна полной подъемной силе F, приложенной в центре давления тела D и направленной вертикально вверх. Очевидно, что в общем случае центр давления тела D и центр его тяжести C не совпадают. Таким образом, всякое тело, погруженное в жидкость, теряет в своем весе столько, сколько весит вытесненная им жидкость, на что и указал Архимед (287 – 212 до н.э.).
Сопоставляя между собой силу F и вес тела G, можно установить следующее:
при F < G — тело тонет;
при F = G — тело плавает в погруженном состоянии;
при F > G — тело всплывает.
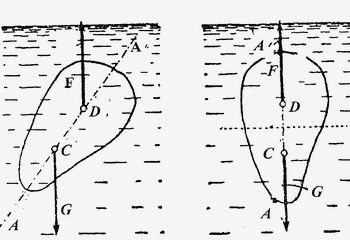
Рис. 6. Равновесие тел, погруженных в воду.Условием равновесия плавающего тела является равенство F = G. Однако, как видно из рис. 6, это условие — необходимое, но не достаточное: при наличии опрокидывающего момента тело будет вращаться. Достаточным условием равновесия является вертикальность линии АА соединяющей точки приложения сил F и G, т. е. центр тяжести C и центр давления D. При этом возможны следующие варианты равновесия:
1) если центр тяжести C тела лежит ниже центра давления D, то равновесие является устойчивым;
2) если центр тяжести C тела лежит выше центра давления D, то равновесие является неустойчивым;
3) если центр тяжести C тела совпадает с центром давления D то равновесие является безразличным (например, плавающий на глубине шар).В заключение рассмотрим типичную школьную задачу на тему закона Архимеда.
Условие. Необходимо определить максимально возможный объем песка V плотностью ρ = 2400 кг/м³, который сможет перевозить баржа шириной B = 5 м и длиной L = 20 м при осадке H = 1,5 м. Собственный вес баржи составляет G = 250 кН.
Решение. По закону Архимеда вес баржи с грузом при максимальном погружении равен выталкивающей силе, поэтому вес песка:
Gпесок = ρgHBL – G = 1000 · 9,81 · 1,5 · 5 · 20 – 250000 = 1,22 MH.
Тогда искомый максимальный объем песка
V = Gпесок / ρg = 1,22 · 106 / 2400 · 9,81 ≈ 52 м³
Из учебника В.А. Винникова и Г.Г. Каркашадзе
«Гидромеханика» (М., 2003).
Знаменательные открытия эпохи Паскаля
1627 г.
Вышел в свет труд Р. Декарта «Рассуждения о методе».1628 г.
Итальянский ученый Б. Кастелли установил закон обратной пропорциональности скорости течения жидкости в трубах площади поперечного сечения.1632 г.
Вышел в свет известный труд Г. Галилея «Диалог о двух основных системах мира – птолемеевой и коперниковой», где, в частности, содержатся два важных принципа современной физики – принцип инерции и принцип относительности.1636 г.
Вышел в свет трактат М. Мерсенна «Универсальная гармония», где изложены его исследования по акустике.1637 г.
Вышел в свет труд Р. Декарта «Диоптрика», где излагается идея эфира как переносчика света, дается теоретическое доказательство закона преломления, которое было высказано Декартом еще в 1630 г. Экспериментально закон преломления установлен в 1621 г. В. Снеллиусом.Р. Декарт ввел понятие переменной величины и функции.
1638 г.
Вышел в свет труд Г. Галилея «Беседы и математические доказательства, касающиеся двух новых областей науки...», в котором, в частности, содержится идея конечности скорости распространения света и постановки эксперимента для ее определения, утверждение, что при отсутствии сопротивления среды все тела падают с одинаковой скоростью; законы свободного падения (пропорциональность скорости падающего тела времени падения, и пропорциональность пройденного пути квадрату времени), закон сложения перемещений и т.п.Итальянский ученый Дж. Б. Бальяни впервые четко разграничивает понятие веса и массы тела и указывает на пропорциональность веса массе.
1643 г.
Открытие атмосферного давления, способа получения вакуума и создание первого барометра (Э. Торричелли).Установление Э. Торричелли формулы для скорости истечения жидкости из узкого отверстия в открытом сосуде (формула Торричелли).
1644 г.
Вышел в свет труд Р. Декарта «Начала философии», в котором впервые четко сформулирован закон инерции, дана теория магнетизма и изложена первая космогоническая гипотеза. Здесь же помещен и его закон сохранения количества движения, но скорость у Декарта была скалярной величиной.М. Мерсенн дал количественное описание наблюдений, выполненных У. Гильбертом.
1646...1647 гг.
Б. Паскаль подтвердил существование атмосферного давления, повторив опыт Торричелли, и экспериментально обнаружил уменьшение атмосферного давления с высотой.1647 г.
Итальянский математик Б. Кавальери в трактате «Шесть геометрических упражнений» дал формулу линзы.1648 г.
Открытие дисперсии света (И. Марци).1650 г.
О. Герике изобрел воздушный насос.1653 г.
Установление Б. Паскалем закона распределения давления в жидкости (закон Паскаля), опубликован в 1663 г.1655 г.
Изобретение ртутного термометра.1657 г.
Х. Гюйгенс сконструировал маятниковые часы со спусковым механизмом, ставшие основой точной экспериментальной техники (проект соединения маятника со счетчиком предлагал Галилей еще в 1636 г.).Изобретен водяной барометр (О. Герике).
1659 г.
Р. Бойль и Р. Гук усовершенствовали воздушный насос Герике.1660 г.
Х. Гюйгенс и Р. Гук установили постоянные точки термометра – точку таяния льда и точку кипения воды.Вышел в свет труд Р. Бойля «Новые опыты..., касающиеся упругости воздуха».
О. Герике сконструировал основанную на трении электрическую машину.
1661 г.
Р. Бойль в труде «Химик-скептик» сформулировал понятие химического элемента как простейшей составной части тела.1662 г.
Р. Бойль открыл зависимость давления газа от объема, Независимо от Бойля этот же закон установил Э. Мариотт в 1676 г. Отсюда и современное название – закон Бойля – Мариотта.П. Ферма сформулировал оптический принцип, названный его именем (принцип Ферма).
1665 г.
Опубликован труд Ф. Гримальди «Физико-математический трактат о свете, цветах и радуге», в котором содержится открытие явления дифракции (интерференции) света.Вышел в свет трактат Р. Гука «Микрография», в котором описаны его микроскопические наблюдения.
И. Ньютон вывел обратно пропорциональную зависимость силы тяготения квадрату расстояния между притягивающимися телами.
1666 г.
Открытие И. Ньютоном явления разложения белого света в спектр (дисперсия света) и хроматической аберрации.1667 г.
Вышел в свет труд Л. Магалотти «Очерки о естественно научной деятельности Академии опытов», в котором изложены результаты коллективной работы, проводимой академиками флорентийской Академии опытов в 1657...1667 гг. Описаны термометры, ареометр, гигрометр, маятник с бифилярным подвесом, опыты по тепловому расширению тел и получению вакуума.Дж. Борелли вывел закон столкновения неупругих тел.
1668 г.
И. Ньютон сконструировал первый зеркальный телескоп (телескоп-рефлектор).1669 г.
Х. Гюйгенс дал теорию удара упругих тел и установил закон сохранения количества движения (mv) и закон «живых сил» (mv2/2).Э. Бартолин открыл двойное лучепреломление света в кристаллах исландского шпата.
Открыт 15-й элемент – фосфор (Г. Брандт).
Немецкий химик И. Бехер выдвинул гипотезу флогистона.
1670...1671 гг.
В сочинении «Метод флюксий» (опубликовано в 1736 г.) И. Ньютон наиболее полно разработал дифференциальное и интегральное исчисления. В 1684 г. систематическое изложение дифференциального исчисления, а в 1686 г. интегрального опубликовал Г. Лейбниц.1672 г.
Вышел в свет труд О. Герике «Новые, так называемые магдебургские опыты о пустом пространстве».Впервые с приемлемой точностью измерено расстояние до Солнца (Ж. Ришар, Д. Кассини).
1674 г.
Р. Гук в трактате «О движении Земли» высказал идею тяготения и представил свою систему мироздания. В 1680 г. Р. Гук пришел к выводу, что сила тяготения обратно пропорциональна квадрату расстояния.Открытие обертонов.
1675 г.
Р. Гук открыл основной закон упругости (закон Гука).И. Ньютон выдвинул корпускулярную гипотезу света.
Исследуя интерференцию и дифракцию света, И. Ньютон открыл так называемые «кольца Ньютона».
1676 г.
О. Ремер в результате наблюдений спутников Юпитера сделал вывод о конечности скорости распространения света и по данным наблюдений впервые определил ее величину – 214000 км/сек, (до этого Дж. Порта, И. Кеплер, Р. Декарт и др. считали скорость света бесконечной).Э. Мариотт предложил рассчитывать высоту места по данным барометра.
Из Летописи познания Ю. Храмова