С.С. Воронков

Общая динамика

ББК22.31
В75
УДК530.1


Воронков С.С.
В75 Общая динамика. – 3-е изд., переработанное. – Псков: Квадрант, 2014. – 301 с.

Общая динамика – интегрирующая наука, включающая классическую, квантовую, релятивистскую механики, электродинамику Максвелла и др.

В основе построения теории лежит признание мировой среды, состоящей из электронов. Определены физические свойства этой среды. Получены уравнения динамики вакуума, представляющие собой нелинейное обобщение уравнений электродинамики Максвелла для вакуума, дополненные уравнением непрерывности и формулой для скорости света.

Уточняются первичные понятия: масса, заряд, тяготение, силы инерции и др. Анализируется возможность перемещения тел под действием сил инерции, механизм возникновения турбулентности, причины вращения Земли вокруг своей оси. Получено следующее приближение закона тяготения Ньютона.

Приводятся механизм передачи электрической энергии, принцип работы генератора Капанадзе, новые электродинамические силы, открытые Николаевым. Дается динамическая интерпретация квантовой механики. Рассматриваются квантовые эффекты на макроуровне, фундаментальные взаимодействия и элементарные частицы.

© С.С. Воронков, 2014
© Квадрант, 2014

Содержание

Предисловие к третьему изданию

Третье издание предлагаемой вашему вниманию монографии «Общая динамика» является переработанным и дополненным. Добавлены две новые главы: «Релятивистская механика» и«Размерности физических величин». В главе8 «Электродинамика» добавлены новые параграфы. Параграф 8.7 «Генератор Капанадзе», в котором рассматривается принцип его работы и показано, что он представляет собой устройство емкостного отбора мощности конденсаторного типа с неявным подключением к линии электропередачи через заземлитель. В параграфе8.8 анализируются новые электродинамические силы, открытые Г. В. Николаевым. В параграфе 8.9 рассмотрен принцип работы магнитного подшипника Николаева.

Прошедший период в шесть лет между первым и третьим изданиями еще более укрепил меня в мысли, что многие «новые» идеи содержатся в работах Дж. К. Максвелла, которые на сегодня никак не устарели и требуют тщательнейшего изучения.

Хочу поблагодарить друзей и коллег за критические замечания, направленные на улучшение работы. Особо благодарю инженера Г. А. Дударева и преподавателя Псковского государственного университета Д. С. Воронкова за техническую помощь при проведении экспериментов и подготовке рукописи, а также за обсуждение некоторых глав работы.

С. С. Воронков
2014 г.

Предисловие к первому изданию

Предлагаемая вашему вниманию монография является результатом обобщения работ [1, 2, 3, 4, 5, 6], опубликованных в период моего заведования кафедрой теплотехники и гидравлики с1991 по2007 годы в Псковском государственном политехническом институте. В Ленинградском политехническом институте (ныне– Санкт-Петербургский государственный политехнический университет), который я закончил в 1979 году и филиалом которого до2004 года был Псковский политехнический институт, на протяжении всего ХХ века среди части специалистов технических специальностей существовало критическое отношение к теории относительности. Назову такие известные имена, как В. Ф. Миткевич, Т. А. Лебедев, А. А. Денисов, точка зрения которых по этому вопросу отражена в их работах [7, 8, 9].

Но с другой стороны, теория относительности, разработанная А. Эйнштейном, во многих областях знаний получила опытное подтверждение. Поэтому, если мы хотим перестроить теорию, то должны при этом сохранить её положительные достижения. Чем руководствоваться при построении теории, что выбрать в качестве главного метода? Ответ на это дают работы Дж. К. Максвелла, который широко использовал при построении своей теории метод электрогидродинамических аналогий. Это была отправная точка моих рассуждений, а что из этого получилось, судить вам.

Хочу поблагодарить коллег по работе, друзей, и особенно, мою жену Лену, за поддержку при написании этой книги. Также благодарю инженеров Г. А. Дударева и Д. С. Воронкова за техническую помощь при проведении экспериментов и подготовке рукописи.

С. С. Воронков
2008 г.

Введение

Однажды рыбы в реке услышали, как люди говорят, будто рыбы могут жить только в воде. Услышав это, рыбы очень удивились и стали спрашивать одна другую: что такое вода? Спрашивали, спрашивали– никто не знает. Тогда одна рыба сказала: « Говорят, в море живёт старая, мудрая рыба, она, должно быть, знает, что такое вода. Поплывём к ней и спросим её». И вот поплыли рыбы в море к тому месту, где жила мудрая рыба и спросили её, что такое вода. И старая мудрая рыба сказала: «Вода – это то, чем мы живём. Вы оттого и не знаете воду, что живёте в ней и с нею». Притча о мудрой рыбе и воде.

Л.Н. Толстой

Мы, люди, не замечаем мировой среды именно потому, что живем в ней и с нею. Мировая среда окружает нас со всех сторон и содержится в нас. Все мироощущение происходит относительно этой среды. Она выступает как бы «нулевым» уровнем, относительно которого ведется отсчет.

Ближе всех к пониманию строения мировой среды подошел в XIX веке Дж. К. Максвелл. В своих работах Максвелл называет эту среду по-разному [10, 11, 12, 13]: электрическая жидкость, светоносная среда, электромагнитная среда, эфир, так называемый вакуум. Но многие идеи Максвелла опередили свое время и не были положительно восприняты современниками. Стиль мышления Максвелла, сочетающий в себе образное и, одновременно, математически строгое описание, в большей мере соответствует нелинейному стилю мышления конца ХХ века. В конце XIX века в науке доминировал линейный, формально-математический стиль мышления. И та электродинамика, которую использовали в ХХ веке и которую называют электродинамикой Максвелла, есть лишь линейный, упрощенный вариант электродинамики, разработанной Максвеллом. Упрощенный вариант электродинамики был разработан в конце XIX века Хевисайдом, Герцем и другими. В начале ХХ века в качестве научной парадигмы была принята теория относительности А. Эйнштейна [14], которая отказалась от «светоносного эфира» и которая довольствовалась линейными, упрощенными уравнениями. Уравнения, полученные Максвеллом [13], являются более общими, нелинейными, и записаны они относительно векторного и скалярного потенциалов.

Не случайно свой «Трактат об электричестве и магнетизме» Максвелл заканчивает размышлениями о мировой среде [13]: «Следовательно, все эти теории ведут к понятию среды, в которой имеет место распространение, и если мы примем эту среду как гипотезу, я думаю, она должна занять выдающееся место в наших исследованиях и следует попытаться построить мысленное представление ее действия во всех подробностях; это и являлось моей постоянной целью в настоящем трактате».

В конце ХХ века произошла смена парадигмы науки. Новая парадигма есть парадигма нелинейности. Новая парадигма требует пересмотра, переформулировки основных положений науки, переосмысления прежних понятий таких, как заряд, масса, тяготение, относительность и др. Необходимо за прежними понятиями увидеть новое содержание.

В предлагаемой вашему вниманию «Общей динамике», исходя из признания мировой среды, разрабатывается интегрирующая теория, охватывающая классическую, квантовую, релятивистскую механики, электродинамику Максвелла и др.

Глава 1. Основные понятия

В этой главе отражены основные философские взгляды, лежащие в основании построения интегрирующей теории.

1.1. Нелинейность как новая парадигма

Нелинейность стремительно ворвалась в нашу жизнь. Во многих дисциплинах, таких как теория колебаний и волн, гидродинамика, синергетика, глобальная экология и др. мы встречаемся с нелинейностью в уравнениях, описывающих реальный мир. В философии заговорили о нелинейном мышлении, нелинейном письме.

Смысл слова «нелинейный» на обыденном уровне можно передать словами: сложный, непредсказуемый. И как ни парадоксально, на сегодня философия и религия точнее, чем наука, отражают сложность, непредсказуемость реального мира. Наука, начиная с Г. Галилея, в мировоззренческом плане – линейна. Революция в физике в начале XX века, выразившаяся в создании специальной теории относительности (СТО), закрепила линейный подход в науке и, тем самым, еще более удалила ее от реальности.

В конце ХХ века произошло осознание сложности, непредсказуемости реального мира, его нелинейности. Произошла смена парадигмы науки. Прежняя парадигма, в основе которой лежали идеи СТО, исчерпала свои положительные возможности. В специальной теории относительности был найден единственно верный формально-математический подход, который, беря за основу линейные уравнения для покоящихся сред и привлекая преобразования Лоренца, позволяет получить, в некоторых частных случаях, верные решения. Но недостатком такого подхода является утрата нелинейных членов в уравнениях. В СТО за основу берутся уравнения Максвелла для покоящихся сред. У Максвелла эти уравнения более общие, и они содержат нелинейные члены.

Выход из сложившейся ситуации лежит в воссоздании целостной картины мира, присутствующей в античной парадигме науки, в возврате к идее мировой среды. Ближе всех в наше время к этой картине мира подошел Дж. К. Максвелл. Нужно вернуться к Максвеллу и пересмотреть многие положения в физике.

Что же представляет собой нелинейность с математической точки зрения?

С линейными и нелинейными функциями мы знакомимся в курсах математики средней школы [15].

Линейной называют функцию [15]

y = ax + b,                 (1.1)

где x − аргумент, a и b − константы.

В случае b = 0 получим прямо пропорциональную зависимость

y = ax.                 (1.2)

График линейной функции есть прямая.

Значение линейной функции при описании физических процессов огромно, так как многие процессы, в первом приближении, описываются линейными зависимостями.

Рассмотрим в качестве примера систему, состоящую из шарика массой m, подвешенного на пружине, массой которой можно пренебречь по сравнению с m (рис.1.1).

Рис. 1.1.

Пусть сила упругости пружины F связана со смещением из положения равновесия линейной зависимостью

F = –kx.                 (1.3)

где k − коэффициент жесткости пружины.

Знак «−» показывает, что сила F всегда направлена к положению равновесия.

Уравнение движения шарика запишется

                (1.4)

Введя обозначение

                (1.5)

запишем (1.4) в виде

                (1.6)

Здесь ω₀ − круговая собственная частота.

Уравнение (1.6) − однородное линейное дифференциальное уравнение второго порядка, описывающее свободные колебания системы с одной степенью свободы.

В качестве еще одного примера линейной системы приведем колебания математического маятника в случае малых амплитуд (рис.1.2).

Рис. 1.2.

Уравнение колебаний запишется [16]

                (1.7)

где φ − угол отклонения; g − ускорение свободного падения; l − длина маятника.

XIX век − век бурного развития наук о природе: термодинамики, гидродинамики, теории упругости, электричества и магнетизма и др. Интенсивно в этот период развивалась и интегрирующая наука − теория колебаний и волн, увенчавшаяся выходом в свет замечательной монографии Рэлея «Теория звука» [17]. Уже в этом труде Рэлей анализирует различные нелинейные системы: автоколебательные, уравнения с переменными коэффициентами. Но в целом особенностью теории колебаний и волн этого периода является линейность рассматриваемых задач. Большинство полученных решений линейных дифференциальных уравнений давали прекрасное совпадение с реальностью. Это укрепляло уверенность в приемлемости такого подхода, и, по существу, он перешел на уровень интуитивного.

Но как справедливо отмечается в [18]: «...в большом числе случаев линеаризация системы, хотя и осуществляемая путем пренебрежения весьма малыми величинами, дает грубое, упрощенное представление действительных процессов с количественными результатами, иногда неприемлемыми даже в ориентировочных расчетах».

Все реальные системы являются нелинейными. Линейность есть результат упрощения реальной системы.

В настоящее время теория нелинейных колебаний и волн значительно продвинулась вперед [19]. В чем же отличие линейных систем от нелинейных?

Нелинейные системы описываются нелинейными дифференциальными уравнениями, в которых неизвестная функция или ее производные входят в степени, отличной от первой. Это приводит к качественному, принципиальному отличию нелинейных систем от линейных. В то же время, значительно усложняется решение нелинейных уравнений, так как в большинстве случаев они не имеют аналитических решений. В качестве примера нелинейной системы приведем колебания математического маятника без ограничений амплитуды.

Уравнение колебаний в этом случае запишется [16]

                (1.8)

где φ − угол отклонения; g − ускорение свободного падения; l − длина маятника.

Рассмотрим подробнее класс систем, занимающих промежуточное положение между линейными и нелинейными системами. Это системы, описываемые линейными дифференциальными уравнениями с периодическими коэффициентами.

Важность этого класса систем обусловлена тем, что к линейным дифференциальным уравнениям с переменными коэффициентами приводят задачи об устойчивости периодических решений нелинейных систем, рассматриваемые в первом приближении [18].

В качестве примера этого класса систем рассмотрим математический маятник с периодически изменяющейся длиной [20]

                (1.9)

где l₀ − средняя длина маятника; a − амплитуда изменения длины маятника; p − частота изменения длины маятника.

В предположении, что амплитуды колебания маятника малы: sin φ ≈ φ и a/l₀ << 1, уравнение колебаний запишется [20]

                (1.10)

Эти колебания называются также параметрическими. Уравнение (1.10) является линейным дифференциальным уравнением с периодическим коэффициентом. В общем случае, если коэффициент в уравнении изменяется по гармоническому закону с частотой р и глубиной модуляции n, уравнение запишется

                (1.11)

Уравнение (1.11) называется уравнением Матье.

Рассмотрим подробнее уравнение Матье с диссипативным членом [21, 22]

                (1.12)

где δ − коэффициент демпфирования.

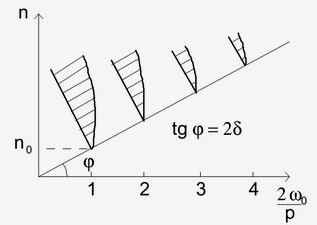
Особенность уравнения (1.12) заключается в том, что при определенных соотношениях параметров его решения неограниченно возрастают во времени. Области в пространстве параметров, при которых решения неограниченно возрастают, называют областями неустойчивости – областями параметрического резонанса. Приведем графики областей неустойчивости, полученные в 1927 г. А.А. Андроновым и М.А. Леонтовичем [21] для уравнения (1.12) (рис.1.3)

Рис. 1.3.

Заштрихованные области − области неустойчивости. Первая заштрихованная область − главная область неустойчивости. При наличии потерь вершины областей неустойчивости поднимаются. Они лежат на прямой, которая составляет угол φ = arctg 2δ с осью абсцисс. Заштрихованные области соответствуют нарастающему процессу с частотой ω = νp/2 ≈ ω₀ (ν = 1, 2, 3, ...). Наиболее существенный факт состоит в том, что уравнение (1.12) имеет возрастающее решение лишь при достаточно больших значениях параметра n. Так, для главной области неустойчивости, неустойчивость возможна лишь при n > n₀ [22]

                (1.13)

При значениях n < n₀ колебания будут затухающими.

Таким образом, параметр n₀ является бифуркационным параметром, определяющим точку разветвления решений.

Особенность параметрических систем состоит также в том, что здесь нет явной внешней силы, приводящей к резонансу. Энергия извне поступает в систему "скрытно", через параметр. Классическим примером параметрических колебаний является раскачивание качелей [20]. Качели можно представить в виде математического маятника переменной длины, описываемого уравнением (1.10). Качели раскачивают, приседая и поднимаясь в такт с качаниями, что равносильно изменению длины маятника.

Итак, выделим следующие важные свойства нелинейных систем.

1. При определенных соотношениях параметров нелинейной системы происходит потеря устойчивости – параметрический резонанс.
2. Особенности нелинейной системы начинают проявляться при переходе через определенное пороговое, критическое значение параметров. Именно благодаря этому свойству нелинейных систем, применимо линейное приближение. Природа как бы скрывает от нас нелинейность, которая тут же проявляется при превышении критического значения параметров.
3. Любые физические константы – лишь первое приближение к реальности. Все они могут зависеть от различных факторов. Так как весьма незначительные изменения констант в уравнениях приводят к качественным изменениям решений, у нас нет оснований принимать их постоянными. Тем более, что никогда нельзя доказать неизменность констант за пределами точности эксперимента.

При построении интегрирующей теории будем использовать, наряду с другими, метод нелинейности, суть которого сводится к следующему.

Метод нелинейности . В основе метода лежит осознание сложности, непредсказуемости реального мира, его нелинейности. Это осознание позволяет сформулировать следующие два положения:

1. линейные законы, описывающие мир, являются лишь первым приближением к реальности;
2. физические константы, линеаризирующие законы, также являются первым приближением к реальности.

Метод нелинейности указывает путь в познании природы, заключающийся в уточнении существующих законов и физических констант, позволяющих вскрыть сложность, непредсказуемость реального мира, его нелинейность. При построении интегрирующей теории важны не сами законы, а отклонения от них.

1.2. Принцип единства мира

В качестве философской основы построения теории примем принцип единства мира, согласно которому, во-первых, мир материален, и в любой части мира структурные единицы материи одинаковы и, во-вторых, в мире существует всеобщая связь вещей и процессов. Объединяющим началом выступает мировая среда – физический вакуум (эфир), «заполняющая» все пространство. Пустого пространства не существует. Это пространство Декарта, отождествляемое с протяженностью материи. Мир един и взаимосвязан. Следовательно, теория, описывающая этот мир, также должна быть единой.

1.3. Пространство

Концепция мировой среды позволяет ввести, по крайней мере, в философском смысле, абсолютную систему отсчета, связанную с самой средой. Действительно, признавая реальность существования мировой среды, мы тем самым упраздняем пустое пространство. Все пространство заполнено мировой средой. То есть это пространство Декарта, которое отождествляется с протяженностью материи. Следовательно, мы можем связать с этой средой систему отсчета. Но эта среда подвижна. В этом случае задача введения абсолютной системы отсчета несколько усложняется, но она решаема.

Для введения абсолютной системы отсчета поступим так, как это делается в механике сплошной среды в случае подвижной среды [23]. Введем две системы: x¹, x², x³ – систему отсчета наблюдателя и сопутствующую систему – ξ¹, ξ², ξ³ , совпадающую в начальный момент времени с первой. Сопутствующая система отсчета представляет собой лагранжевы координаты индивидуальных точек мировой среды. Система координат, связанная с частицами мировой среды, с течением времени будет изменяться, так как среда подвижна. « Выбор такой системы координат, − как отмечает Л.И. Седов [23], − в любой данный момент времени в нашей власти, но в последующие моменты она уже не подвластна нам, так как она "вморожена" в среду и деформируется вместе с ней».

Зная законы движения каждой точки мировой среды

ξ ⁱ = ξ ⁱ (x¹, x², x³, t)     i = 1, 2, 3,             (1.14)

мы сможем определить положение мировой среды в системе отсчета наблюдателя

x ⁱ = x ⁱ (ξ¹, ξ², ξ³, t)     i = 1, 2, 3,             (1.15)

и тем самым однозначно задать абсолютную систему отсчета x¹, x², x³ .

Такой выбор системы отсчета соответствует, фактически, выбору в качестве абсолютной системы фиксированного положения мировой среды во вселенной при известном законе изменения последующих состояний.

Ясно, что реализовать на практике такой подход весьма сложно, так как для этого потребовалось бы проследить все существующие связи во вселенной, но теоретически, в философском смысле, он позволяет ввести абсолютную систему отсчета.

1.4. Время

В специальной теории относительности вводится относительное время, которое ничего не имеет общего с физической реальностью. Преобразования Лоренца являются формально-математическими преобразованиями, относительно которых инвариантны линейные, упрощенные уравнения. Необходимо отказаться от преобразований Лоренца и относительного времени и вернуться к нелинейным, более точным уравнениям Максвелла и абсолютному времени.

В понятии времени необходимо выделить понятие длительности. Время, как длительность, это свойство материи. Из принципа единства мира следует, что в любой части мира существует эталон длительности − атомные часы. Но понятие времени шире, оно включает также порядок последовательности событий. Согласно принципу единства мира, в мире существует всеобщая связь вещей и процессов. Следовательно, всегда можно выделить такое состояние мира, которое предшествует последующему состоянию. Это состояние мы и называем одновременным. Как точно отмечает Дж. Уитроу [24]: «...мы считаем события одновременными не потому, что они приходятся на один и тот же момент времени, а поскольку они совместно происходят». Как отметил Дж. Ганн [24]: «мы устанавливаем время из событий, а не наоборот».

Наличие в любой части мира эталона длительности и всеобщей связи процессов, то есть абсолютной одновременности, позволяет ввести абсолютное время и отказаться от относительного времени, введенного в специальной теории относительности и не отражающего объективных связей природы.

Глава 2. Базис общей динамики

Общая динамика – интегрирующая наука, включающая в себя как составные элементы классическую, квантовую, релятивистскую механики, электродинамику Максвелла и др. Построение интегрирующей науки позволит устранить противоречия в частных науках и продвинуться вперед в понимании природы.

В этой главе будут рассмотрены проблемы, существующие в классической, квантовой, релятивистской механиках, электродинамике Максвелла и др.

2.1. Классическая механика

В основе классической механики лежат три закона Ньютона и закон всемирного тяготения [25], в которых определены инертная и гравитационная массы. Но в рамках классической механики не удается обосновать равенство инертной и гравитационной масс, понять причины сил тяготения. Как отмечает Максвелл [26]: «…одно из первых, если не самое первое, требование полной теории материи есть объяснение, во-первых, массы и, во-вторых, тяготения».

Законы Ньютона выполняются в инерциальных системах отсчета. В неинерциальных системах отсчета для пользования вторым законом Ньютона в него необходимо ввести дополнительно переносные и кориолисовы силы инерции. Этот прием выглядит искусственно и требует дополнительных обоснований. Что представляют собой силы инерции, фиктивны или реальны они? Выполняется ли третий закон Ньютона для сил инерции? Это вопросы, которые давно сформулированы, но 23 не могут быть разрешены в рамках классической механики. Сформулируем вопросы в следующем виде:
        – Что такое масса и тяготение?
        – Что представляют собой переносные и кориолисовы силы инерции?

2.2. Квантовая механика

Основным уравнением квантовой механики является уравнение Шредингера [27]. Состояние квантовых объектов характеризуется волновой функцией − ψ , относительно которой записано уравнение. Энергетические уровни, спектры атомов получаются как решения этого уравнения. Постоянная Планка введена в уравнение как константа, благодаря чему эффект квантования получает физически наглядное истолкование. По этому поводу Планк отметил [28]: «Это первый случай, когда квант действия, который до сих пор не поддавался никаким попыткам подойти к нему с точки зрения физики непрерывного, удалось включить в дифференциальные уравнения. Ибо ранее он появлялся всегда только в таких соотношениях, которые содержали конечные разности или конечные интегралы».

Выпишем стационарное уравнение Шредингера [29]

                (2.1)

где ψ − волновая функция, m – масса частицы, ћ – постоянная Планка, U – потенциальная энергия в силовом поле, Е – общая энергия частицы.

Шредингер свое знаменитое уравнение постулировал на основе вариационного принципа [27]. То есть Шредингер решил обратную задачу, по известным опытным данным спектров атомов он нашел уравнение, решения которого приводят к этим спектрам, и записал его относительно произвольной функции ψ . В первой своей работе о сущности функции ψ он пишет [27]: «Довольно естественно связывать функцию ψ с некоторым колебательным процессом в атоме...». В дальнейшем, по поводу интерпретации функции ψ , среди основателей квантовой механики, возникли серьезные разногласия. В настоящее время предпочтение отдается статистической интерпретации волновой функции [30], хотя сам Шредингер с этой интерпретацией так и не согласился.

Многие основатели квантовой механики выступали против отказа от традиционных подходов в науке. Так в [31] отмечается: « Едва ли не большинство создателей квантовой механики − Планк и Эйнштейн, де Бройль и Шредингер, Гейзенберг и Дирак, − в разное время и в разной форме возражали против отхода от классических принципов». В качестве примера приведем известную беседу основателя квантовой механики М. Планка с А.Ф. Иоффе [32], занимающимся разработкой вопросов квантовой механики. «Мы столь многим обязаны Максвеллу, что было бы неблагодарным отказаться от его теории, − говорил он молодому А.Ф. Иоффе [32]. − Попробуйте, нельзя ли добиться таких же выводов, не порывая с Максвеллом».

Шредингер надеялся вывести свое уравнение из классических уравнений электродинамики, но это ему не удалось сделать. Так, в [33] он пишет: « Есть даже некоторая надежда на то, что после этого волновое уравнение для ψ точно так же может быть получено в качестве следствия уравнений Максвелла − Лоренца, а именно как уравнение непрерывности электричества».

В дальнейшем будет показано, что уравнение Шредингера выводится из уравнений динамики вакуума, и здесь возникает вопрос:
        − Что представляет собой волновая функция ψ ?

2.3. Релятивистская механика

Релятивистская механика основана на специальной теории относительности, разработанной А. Эйнштейном [14].

Согласно теории относительности, законы природы инвариантны относительно преобразований Лоренца. Применяя преобразования Лоренца к законам механики, электродинамики и др., мы получаем релятивистские эффекты, подтвержденные опытом. Релятивистские эффекты проявляются в появлении в формулах релятивистского множителя , как, например, в формуле для релятивистского импульса

                (2.2)

где m – масса тела, v – скорость тела, с– скорость света в вакууме.

Но вся проблема заключается в том, что преобразования Лоренца сохраняют инвариантными лишь линейные уравнения. Линейные уравнения описывают мир в первом приближении. Для иллюстрации воспользуемся примером из механики жидкости и газа. В линейном приближении процессы в жидкостях и газах описываются уравнениями акустики. Но если среда подвижна и амплитуды изменения параметров существенны, мы вынуждены привлекать более точные уравнения: Эйлера, Навье–Стокса, Рейнольдса и другие, учитывающие различные нелинейные эффекты. Относительно преобразований Лоренца инвариантны лишь уравнения акустики. Но что интересно, решения более сложных уравнений (Эйлера, например), полученные без привлечения преобразований Лоренца, с точностью до произвольной постоянной совпадают с решениями, полученными из уравнений акустики с привлечением преобразований Лоренца [5]. Эта аналогия подсказывает нам путь дальнейшего развития теории. Необходимо проанализировать уравнения Максвелла и учесть в них различные нелинейные эффекты. Особенность нелинейных эффектов заключается в том, что их учет может приводить не только к количественному изменению решений, а и к принципиально качественному изменению. Если удастся из измененных уравнений Максвелла с учетом нелинейных членов получить те же релятивистские эффекты, что и в теории относительности, то это будет свидетельствовать о правильности выбранного подхода.

Сформулируем вопрос:
        − Как необходимо изменить уравнения Максвелла, чтобы релятивистский множитель появлялся естественным образом в решении этих уравнений без привлечения преобразований Лоренца?

2.4. Электродинамика Максвелла

Максвелл при записи уравнений электродинамики широко использовал векторный A и скалярный φ потенциалы [13]. Максвелл называет векторный потенциал A электромагнитным импульсом в точке. Надо полагать, по аналогии с механическим импульсом. Но окончательно физический смысл векторного и скалярного потенциалов так и не был установлен, что предстоит еще сделать.

Более широкое признание получила форма записи уравнений электродинамики в переменных напряженностей E и H, данная Герцем и Хевисайдом. Векторный и скалярный потенциалы в современной теории рассматриваются как вспомогательные математические потенциалы, облегчающие решение системы дифференциальных уравнений.

В теории относительности за основу берутся уравнения Максвелла для покоящихся сред. У Максвелла эти уравнения более общие, и они содержат нелинейные члены. Так уравнение для напряженности электрического поля у Максвелла в современных обозначениях выглядит [13]

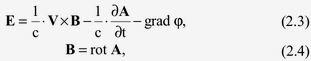
где E − напряженность электрического поля; B − магнитная индукция; V − скорость контура или системы отсчета; c − скорость света в вакууме; A − векторный потенциал; φ − скалярный потенциал.

Первый член в правой части уравнения (2.3), по существу, представляет конвективную производную от векторного потенциала и является нелинейным членом.

Необходимо вернуться к форме записи уравнений электродинамики, используемой самим Максвеллом относительно векторного и скалярного потенциалов с учетом нелинейных членов в уравнениях и ответить на вопрос:
        − Что представляют собой векторный A и скалярный φ потенциалы?

2.5. Альтернативные теории

Сегодня фундаментальная наука находится в кризисе. Но кризис не следует воспринимать как что-то плохое, отрицательное. Как показал Кун [34], сама наука также развивается по сложным нелинейным законам, с периодически возникающими кризисами-революциями, и как выход из этих состояний, – созданием новой парадигмы. Выделим некоторые симптомы современного кризиса в науке:

1. Возникновение неудач при решении технических проблем. В качестве примера приведем попытки осуществить управляемый термоядерный синтез, растянувшиеся на многие десятилетия.
2. Мировоззренческий кризис, связанный с упрощенным, линейным представлением связей в природе и, на этом фоне, парадоксальностью реальности, и осознанием сложности, непредсказуемости реального мира, его нелинейности.
3. Стремительный рост альтернативных теорий и критики теории относительности, исполняющей роль парадигмы современной науки.

Эти симптомы являются предвестниками близкой смены существующей парадигмы науки.

Каждая альтернативная теория заслуживает внимания и глубокого изучения, так как, во-первых, одна из них займет в будущем место официальной парадигмы и, во-вторых, в каждой из них есть критическая мысль, часто дающая значительно больше, чем тома переписанных учебников.

Здесь назовем только некоторые, соответствующие требованиям, предъявляемым к альтернативным теориям. Это: «Общая теория» Вейника [35], «Общая эфиродинамика» Ацюковского [36], «Теория физического вакуума» Шипова [37] и др. В этих работах рассматриваются различные решающие эксперименты, призванные рассудить, какая из теорий соответствует природе вещей. Особо выделим инерцоид Толчина [38], перемещающийся под действием сил инерции, чего не может быть с точки зрения классической механики, и рассматриваемый в работе[37]. Сформулируем следующий вопрос:
        − Возможно ли перемещение тел под действием сил инерции?

Глава 3. Свойства мировой среды

Мировая среда представляет собой сплошную непрерывную среду, заполняющую все пространство. Но почему на макроуровне мы не замечаем этой среды, не замечаем ее проявлений? Из каких структурных элементов она состоит? Каковы физические свойства этой среды? Попробуем ответить на эти вопросы.

3.1. Что представляет собой мировая среда?

Трактат по электричеству и магнетизму Максвелла [13] пронизан признанием среды, в которой происходят электромагнитные процессы.

Рассмотрим некоторые опытные данные, ведущие к признанию мировой среды, содержащиеся в электродинамике Фарадея-Максвелла и приводимые в их работах [13,39].

1. Ток проводимости
Электрическим током называется упорядоченное движение электрических зарядов. Если упорядоченное движение зарядов возникает в проводнике, например, в металле, то электрический ток называется током проводимости.

Сегодня известно, что носителями электрических зарядов в металлах являются электроны, и ток проводимости представляет собой перемещение электронов внутри проводника.

В период написания «Трактата» еще не была установлена природа электрического тока, и Максвелл придерживался феноменологического подхода при описании. При этом для понимания происходящих процессов он широко привлекал метод аналогий.

В главе «О самоиндукции тока» [13] Максвелл цитирует Фарадея [39]: «Первая мысль, которая приходит в голову, состоит в том, что циркулирующее в проводе электричество обладает чем-то, похожим на импульс или инерцию». «Действительно, – отмечает Максвелл [13], – когда мы рассматриваем один-единственный провод, то явления в точности аналогичны явлениям в трубе, наполненной водой, текущей непрерывным потоком. Если при протекании потока воды быстро закрыть конец трубы, то импульс воды создает резкое повышение давления, значительно превышающее давление, обусловленное перепадом уровней воды, что может привести к разрыву трубы». Но имеются существенные отличия электрического тока от движения воды в трубе. «Эффекты, – пишет Максвелл [13], – связанные с инерцией жидкости в трубе, зависят лишь от количества протекающей через трубу жидкости, от длины трубы и от ее поперечного сечения на разных участках. Они не зависят от всего, что находится вне трубы, а при неизменной длине трубы – от того, как труба изогнута. В случае провода с током положение иное, – поскольку эффект очень мал, если длинный провод сложен вдвое; эффект больше, если эти две части разнесены друг от друга, он еще больше, если провод свернут в спираль, и максимален, если внутрь такой спиральной катушки поместить кусок мягкого железа».

«Итак, − констатирует Максвелл [13], − система, содержащая электрический ток, является, по-видимому, вместилищем какого-то вида энергии, и, поскольку мы не можем создать себе иного представления об электрическом токе, кроме как о явлении кинетическом, его энергия должна быть кинетической, то есть энергией, которой движущееся тело обладает благодаря своему движению. Мы уже показали, что электричество в проводе нельзя рассматривать как некое движущееся тело, в котором и следует отыскивать эту энергию, ведь энергия движущегося тела ни от чего, находящегося вне тела, не зависит, в то же время присутствие около тока других тел меняет его энергию. Мы, таким образом, подошли к вопросу о том, не может ли существовать какого-либо движения вне провода в пространстве, не занятом электрическим током, в котором проявляются электромагнитные эффекты тока».

Если принять эту точку зрения, согласно которой вне провода, при наличии в нем электрического тока, также должно существовать какое-то движение, то мы вправе поставить вопрос: что будет двигаться вне провода, когда провод находится в вакууме?

С точки зрения Максвелла вакуум − диэлектрик, отличающийся от других диэлектриков лишь диэлектрической проницаемостью. Видимо, для того чтобы подчеркнуть, что слово «вакуум» − пустота, используется условно, Максвелл при упоминании о вакууме пишет [13]: «так называемый вакуум».

2. Ток смещения
Важной отличительной особенностью электродинамики Максвелла является введение в уравнения электромагнитного поля электрического смещения и тока смещения. «Если электродвижущая сила воздействует на проводящую среду, − пишет Максвелл [13], − она вызывает в ней ток, если же среда не проводящая или диэлектрическая, то ток не может длительно по ней течь, но электричество смещается в среде в направлении электродвижущей напряженности, причем величина этого смещения зависит от величины напряженности, так что при увеличении или уменьшении электродвижущей напряженности в том же отношении увеличивается или уменьшается электрическое смещение. Изменение электрического смещения, очевидно, представляет собой электрический ток. Однако этот ток может существовать лишь пока меняется смещение, а так как смещение не может превосходить определенного значения, не вызывая пробоя, то ток не может идти неограниченно долго в одном направлении, подобно току проводимости».

Далее Максвелл отмечает: «Чем бы ни являлось электричество, и что бы мы ни понимали под движением электричества явление, называемое электрическим смещением, представляет собой движение электричества в том же смысле, в каком и перенос определенного количества электричества по проволоке является движением электричества. Единственное отличие заключается в том, что в диэлектрике имеется сила, называемая нами электрической упругостью, действующая против электрического смещения и заставляющая электричество возвращаться назад при устранении электродвижущей силы, тогда как в проводниках эта электрическая упругость непрерывно преодолевается, так что устанавливается истинный ток проводимости и сопротивление зависит не от полного количества электричества, смещенного со своего положения равновесия, а от количества электричества, пересекающего сечение проводника в заданное время». Таким образом, по Максвеллу ток проводимости отличается от тока смещения лишь тем, что в диэлектриках имеется «электрическая упругость», действующая против электрического смещения.

Сегодня мы знаем, что носителями электричества в проводниках являются электроны. В диэлектриках, например, газах, под действием электрической напряженности происходит электрическое смещение положительных и отрицательно заряженных частиц. Но так как ток смещения возникает и в вакууме, мы вправе поставить вопрос: смещение какой субстанции происходит под действием электрической напряженности в вакууме?

Из рассуждений Максвелла вытекает, что принципиальных различий между электричеством в проводнике и электричеством в диэлектрике − вакууме, нет. Различие заключается в их состоянии. В проводнике электричество под действием электрической напряженности перемещается, в то время как в диэлектрике электричество подвержено действию электрической упругости и может только смещаться. Но раз электрический ток в проводниках представляет собой движение электронов, то не является ли электрическое смещение в вакууме смещением тех же электронов?

3. Магнитное поле
Как установил Эрстед, при прохождении по проводнику электрического тока вокруг него возникает магнитное поле.

Для выяснения природы магнетизма в главе «Магнитное действие на свет» [13] Максвелл обращается к опыту, предложенному Фарадеем и описывает его: «Луч плоскополяризованного света пропускается через прозрачную диамагнитную среду, а плоскость его поляризации на выходе из среды устанавливается путем наблюдения положения анализатора, при котором луч отсекается. Затем прикладывается магнитная сила, которая действует таким образом, что направление магнитной силы внутри прозрачной среды совпадает с направлением луча. Свет тотчас же появляется вновь, но при повороте анализатора на определенный угол свет опять отсекается. Это показывает, что действие магнитной силы состоит в повороте плоскости поляризации вокруг луча, взятого в качестве оси, на определенный угол, измеряемый углом, на который надо повернуть анализатор, чтобы отсечь свет».

Анализируя описанное явление, Максвелл отмечает: «Изучение действия магнетизма на поляризованный свет приводит, как мы уже видели, к выводу о том, что часть явления, происходящего в среде под действием магнитной силы, составляет нечто относящееся к той же математической категории величин, что и угловая скорость, ось которой направлена вдоль магнитной силы. Эта угловая скорость не может быть скоростью какой-либо части среды, имеющей заметные размеры и вращающейся как единое целое. Мы должны, следовательно, представлять его как вращение очень маленьких объемов среды, каждый из которых вращается вокруг своей собственной оси. Это и составляет гипотезу молекулярных вихрей».

В заключение Максвелл пишет: «Я думаю, что у нас есть хорошие основания полагать, что какое-то явление вращения имеет место в магнитном поле; в этом вращении участвует большое число очень маленьких порций вещества, вращающихся каждая вокруг своей собственной оси, причем эта ось параллельна направлению магнитной силы, и вращения этих вихрей зависят одно от другого, будучи связаны посредством некоторого механизма».

Анализ описанных опытов электродинамики Фарадея-Максвелла позволяет сделать следующие выводы:
        − мировая среда − вакуум обладает физическими свойствами, в ней возможны электрическое смещение и вращение;
        − изменение электрического смещения подобно току проводимости.

Так как электрический ток в проводнике представляет собой движение электронов, учитывая, что изменение электрического смещения подобно току проводимости, естественен следующий вывод:
        − ток смещения в вакууме представляет собой смещение электронов, то есть мировая среда состоит из электронов.

Рассмотрим теперь некоторые опыты квантовой механи-ки, ведущие к представлению о физическом вакууме.

4. Эффект Комптона
Эффект Комптона состоит в изменении длины волны электромагнитных волн при рассеянии их на свободных электронах. Эффект открыт в 1922 г. американским физиком А. Комптоном [40].

Изменение длины световой волны определяется по формуле

                (3.1)

где − комптоновская длина волны электрона; h − постоянная Планка; m_e − масса электрона; c – скорость света; θ – угол рассеяния.

Согласно классической теории рассеяния света длина световой волны при рассеянии не должна меняться.

Мы обратим внимание на появление в этой формуле длины волны λ_k , которая определяет масштаб пространственных неоднородностей полей, при которых становятся существенными квантовые процессы.

Как отмечает Блохинцев [30]: «Эта длина имеет фундаментальное значение в релятивистской теории электрона, являясь одним из масштабов, свойственных микромиру».

Для электромагнитного поля, длина волны которого λ меньше комптоновской длины волны электрона λ_k , становятся существенными процессы рождения электрон-позитронных пар из вакуума [40].

Следовательно, для вакуума имеется характерная длина волны λ_k и при λ < λ_k вакуум качественно изменяет свое состояние- происходит рождение электрон-позитронных пар.

5. Нулевые колебания
Согласно квантовой теории наименьшая энергия гармонического осциллятора равна [30]

                (3.2)

где − собственная частота осциллятора.

Наименьшая энергия осциллятора называется нулевой энергией. Существование нулевой энергии установлено на опыте. « Экспериментально, − отмечает Блохинцев [30], − удается доказать наличие нулевой энергии и нулевых колебаний атомов путем наблюдения рассеяния света кристаллами. Рассеяние света обусловлено колебаниями атомов. По мере уменьшения температуры амплитуда колебаний, согласно классической теории, должна неограниченно уменьшаться, а вместе с тем должно исчезать и рассеяние света. Между тем опыт показывает, что интенсивность рассеяния света по мере уменьшения температуры стремится к некоторому предельному значению, указывающему на то, что и при абсолютном нуле колебания атома не прекращаются. Этот факт подтверждает существование нулевых колебаний».

Но нулевые колебания присущи не только гармоническому осциллятору, а происходят и в вакууме. Как отмечает Блохинцев [30]: «В настоящее время эти эффекты (нулевые колебания электромагнитного поля и поляризация вакуума) получили экспериментальное подтверждение и являются доказательством изумительного факта: в вакууме существуют постоянные нулевые колебания подобно тому, как они существуют в твердом теле, более того, из-за образования пар позитронов и электронов и последующей их аннигиляции происходит поляризация этого вакуума».

Так как нулевые колебания, происходящие в вакууме, установлены экспериментально, то мы вправе поставить вопрос: что колеблется в вакууме?

6. Поляризация вакуума
Поляризация вакуума − явление, заключающееся в рождении виртуальных пар заряженных частиц − античастиц из вакуума под влиянием заряженной частицы [40]. Этот эффект аналогичен поляризации диэлектрической среды внесенным в нее зарядом, что обусловило название явления.

Как отмечает Мигдал [41]: «Когда к электромагнитному полю и к полям, описывающим пары частиц (электрон-позитрон, протон-антипротон и т.д.) применили квантовую механику, оказалось, что в пустоте происходят непрерывные колебания электромагнитного поля, рождаются и исчезают элементарные частицы. При столкновениях нуклонов (нейтронов и протонов) из пустоты возникает целый сноп различных частиц– вакуум полон частиц. По существу, физики снова вернулись к понятию эфира, но уже без противоречий. Удивительно сложную и интересную среду − вакуум − можно было бы снова назвать эфиром, если бы не боязнь путаницы с наивным понятиемXIX века».

Впервые идею о том, что вакуум состоит из электронов, высказал Дирак [42]. «Я попытаюсь, − пишет Дирак, − описать новое представление о физическом вакууме. Согласно этим новым представлениям, вакуум не является пустотой, в которой ничего не находится. Он заполнен колоссальным количеством электронов, находящихся в состоянии с отрицательной энергией, которое можно рассматривать как некий океан».

Таким образом, представления о вакууме физики ХХ века близки с представлениями, вытекающими из электродинамики Фарадея-Максвелла. Проведенный анализ позволяет сделать следующий вывод:
        − Мировая среда − физический вакуум состоит из электронов.

3.2. Плотность

Определим свойства мировой среды. Мы пришли к выводу, что мировая среда состоит из электронов. Известно, что в этой среде распространяются электромагнитные волны, которые являются поперечными. Следовательно, эта среда должна быть сплошной непрерывной средой в буквальном смысле, в которой электроны сохраняют ближний порядок.

Установив, что мировая среда состоит из электронов и что это сплошная непрерывная среда, мы тем самым определили ее плотность, которая равняется плотности электрона

                (3.3)

где m_e = 0,911 · 10 ^–30 кг – масса электрона, V_e − объем электрона.

Но трудность здесь заключается в том, что мы не знаем точно размеров электрона и, соответственно, его объема. Радиус электрона, равный [43] r_e = 2,82 · 10 ^–15 м и называемый классическим радиусом электрона, не есть его геометрический размер, так как он определен из электростатической модели. В действительности, как отмечается в [43]: «экспериментально пока не удалось обнаружить "размеров" у электрона, хотя точность измерений доведена до 10 ^–18 м». Это, видимо, объясняется тем, что электроны (мировая среда) являются средой – «переносчиком» информации, и измерение прямыми методами в этой среде ее структурных единиц затруднено.

Найдем диапазон возможных значений плотности мировой среды, приняв в качестве радиуса электрона значения r_e = 2,82 · 10 ^–15 м и r_e = 10 ^–18 м, Тогда

                (3.4)

Диапазон возможных значений плотности мировой среды весьма широк. Желательно определить значение плотности с большей точностью. В дальнейшем, в параграфе 5.1, при выводе второго закона Ньютона из уравнений динамики вакуума, будет показано, что для совпадения выводимого закона со вторым законом Ньютона необходимо, чтобы плотность мировой среды следующим образом соотносилась с плотностью нейтрона

                (3.5)

где η_n – плотность нейтрона, m_n = 1,675 · 10 ^–27 кг − масса нейтрона, V_n = 1,15 · 10 ^–44 м³ – объем нейтрона при радиусе нейтрона r_n = 1,4 · 10 ^–15 м.

Учитывая, что масса электрона m_e известна с достаточной точностью, из (3.5) найдем объем электрона

          (3.6)

Мировая среда представляет собой сплошную непрерывную среду, в которой электроны сохраняют ближний порядок и отсутствуют какие либо пустоты. По форме электроны должны соответствовать этим требованиям. Этим требованиям соответствуют выпуклые параллелоэдры, которыми можно заполнить все бесконечное пространство, не оставляя пустоты, и без того, чтобы их внутренние объемы пересекались.

Простейшим из них является куб. Приняв в качестве формы электрона куб, найдем линейный размер электрона

                (3.7)

где a_e – линейный размер электрона.

Таким образом, уточненное значение плотности электрона и соответственно мировой среды равно

          (3.8)

Мы получили для плотности мировой среды весьма большую величину, противоречащую нашему обыденному опыту. Например, плотность стали, составляет 7,8 · 10³ кг/м³ , что значительно меньше плотности, полученной для мировой среды (3.8). Но может, мы не замечаем мировой среды именно потому, что она везде нас окружает и во всем содержится?

Действительно, электроны являются составными элементами всех атомов, молекул, тел. Если электроны также являются составными элементами мировой среды, то не может инерционность тел быть результатом взаимодействия тела с мировой средой? Мы знаем, что масса тела – это мера вещества. Но, с другой стороны, масса тела выступает как мера инертности и мера гравитационного взаимодействия. В релятивистской механике масса зависит от скорости

                (3.9)

где m₀ − масса покоя, β = v/c, v − скорость тела, c − скорость света в вакууме.

Есть определенное противоречие между определением массы как меры вещества и определением релятивистской массы по формуле (3.9). Если мы принимаем эти два определения массы, то получается зависимость количества вещества от скорости, что противоречит закону сохранения массы. В некоторых работах [44, 45] предлагается отказаться от определения массы по формуле (3.9), а пользоваться релятивистским импульсом

                (3.10)

где масса m является инвариантом.

Такой подход отчасти оправдан, так как он устраняет существующее противоречие в определениях массы.

Но противоречие также можно устранить, если определить массу как меру взаимодействия вещества с мировой средой. Мировая среда – это среда, в которой совершаются все процессы, и все мироощущение происходит относительно этой среды. Эта среда выступает как бы нулевым уровнем, относительно которого ведется отсчет. Инерционность тела есть не что иное, как мера взаимодействия этого тела с мировой средой. Наделяя тело свойством инерционности, мы тем самым освобождаем себя от необходимости думать об этой среде.

В дальнейшем мы покажем, что принятое определение массы:
        − масса – мера взаимодействия вещества с мировой средой,
позволяет получить формулу (3.9) из уравнений динамики вакуума и тем самым объяснить зависимость массы от скорости как результат взаимодействия с мировой средой.

Выводы:
        − Приняв, что мировая среда состоит из электронов, мы тем самым определили ее плотность, которая равна плотности электрона.
        − Масса – мера взаимодействия вещества с мировой средой.

3.3. Магнитное поле

Что представляет собой магнитное поле в концепции мировой среды? Из электродинамики Фарадея-Максвелла, как было показано в параграфе3.1, следует, что в магнитном поле происходит какое-то явление вращения, в котором участвуют большое число очень маленьких порций вещества, вращающихся каждая вокруг своей собственной оси. К аналогичному выводу пришел Миткевич в своей работе [7]: «На данном этапе наших знаний об электромагнитных явлениях можно, следовательно, считать в высокой степени вероятным, что магнитные линии представляют собой именно замкнутые вихревые нити в эфире».

Максвелл магнитную индукцию B определял через векторный потенциал A [13]

B = rot A                 (3.11)

где A − векторный потенциал.

Количественно вращение в сплошной подвижной среде определяется циркуляцией скорости rot V. Связывая магнитную индукцию B с вращением в мировой среде, примем, что

B = rot (η · V)                 (3.12)

где η − коэффициент, V − скорость мировой среды.

Из сравнения (3.11) и (3.12) видно, что для векторного потенциала мы принимаем

A = η · V                 (3.13)

Что представляет собой коэффициент η в формуле(3.13)?

Выпишем уравнение Максвелла для напряженности E электрического поля в виде

                (3.14)

Найдем силу F, действующую на электрон в электрическом поле, подставляя (3.13) в (3.14) и учитывая, что заряд электрона постоянный и отрицательный

                (3.15)

где e – заряд электрона.

С другой стороны, сила, действующая на электрон массой m_e , определится по второму закону Ньютона

                (3.16)

Сравнивая (3.15) и (3.16), найдем выражение для коэффициента η

                (3.17)

Следует отметить, что векторный потенциал, являющийся в современной физике вспомогательной величиной, в концепции Максвелла играл фундаментальную роль. В разных местах трактата [13] Максвелл называет этот вектор электромагнитным импульсом в точке, надо полагать, по аналогии с механическим импульсом. Действительно, принятое нами выражение для векторного потенциала (3.13) с учетом (3.17)

                (3.18)

фактически является механическим импульсом электрона, отнесенным к его электрическому заряду e.

Вывод:
          − Векторный потенциал является электромагнитным импульсом и определяется скоростью мировой среды.

3.4. Электрический заряд

Различают два вида электрических зарядов [40], условно называемых положительными и отрицательными. Одноименно заряженные тела отталкиваются, разноименно заряженные – притягиваются. Заряд электрона принят в качестве отрицательного и представляет собой элементарный электрический заряд, количественно равный e = 1,6021892(46) · 10 ^–19 Кл.

Первоначально под зарядом тела понималось то, что оно получало в процессе заряжания. По Франклину [46], электричество, которое получается путем увеличения количества электрической материи в теле, называется положительным, а то, которое получается путем ее уменьшения, отрицательным. Но, перенеся свойство, способность макротел быть заряженными на элементарные частицы, мы не добавили ясности, а только все усложнили.

Эта проблема точно подмечена в работах Шаляпина [47]: «Нетрудно заметить, что при введении терминов" электрическая жидкость" и "заряд" в отношении электрона и других микрочастиц появляется явное как логическое, так и семантическое противоречие, поскольку макроскопическое свойство многих тел, а именно, способность "заряжаться" были перенесены на отдельный электрон. При этом "заряд" приобрел некую реальность вне зависимости от материальных объектов. Получается так, что любое тело, а в равной степени и электрон можно зарядить "зарядом". Здесь явно просматривается неверное использование русского языка, поскольку зарядить материальный объект можно чем угодно, но только не зарядом».

В концепции мировой среды мы исходим из того, что эта среда состоит из электронов. Но если электроны обладают отрицательным зарядом, то возникает вопрос: почему этот отрицательный заряд внешне никак не проявляется и что, вообще, представляет собой заряд?

Максвелл считал заряд элементарной частицы понятием вспомогательным, временным. Так в [13] он отмечает: «...теория молекулярных зарядов может рассматриваться как некоторый метод, помогающий нам запомнить множество фактов, относящихся к электролизу. Однако кажется крайне невероятным, что мы сохраним в какой-либо форме теорию молекулярных зарядов после того, как придём к пониманию истинной природы электролиза, ибо тогда у нас будут надёжные основания, на которых можно построить верную теорию электрических токов и тем самым избавиться от этих предварительных теорий».

Необходимо определить ту физическую категорию, к которой следует отнести«электрический заряд».

Мы не случайно в параграфе 3.3 выбрали обозначение для коэффициента η , совпадающее с обозначением плотности мировой среды. В параграфе 3.3 показано, что плотность мировой среды η , с другой стороны, равна η = m_e/e . Сравнивая (3.3) и (3.17) найдём соотношение между зарядом и объёмом электрона

e Кл = V_e м³                 (3.19)

то есть заряд в 1 Кл соответствует объёму мировой среды

                (3.20)

Аналогия между электродинамикой и гидродинамикой подсказывает, что постоянный электрический ток в проводнике тождественен объемному расходу мировой среды через этот проводник. Действительно, зная заряд Q, прошедший через сечение проводника площадью S, с учетом (3.20), объем мировой среды V определится

V = k_Q · Q .                 (3.21)

Рассматривая заряд Q, прошедший через сечение проводника в единицу времени, получим

V' = k_Q · I ,                 (3.22)

где I − сила тока, V' − объемный расход мировой среды.

Для удельных величин, отнесенных к площади S сечения проводника, учитывая, что принятое направление тока [43] противоположно направлению движения электронов, в общем случае будем иметь

V = –k_Q · j ,                 (3.23)

где V − среднерасходная скорость мировой среды в проводнике, j − плотность тока.

Рассмотрим, что представляет собой объемная плотность электрического заряда. По определению

                (3.24)

Здесь ρ − объемная плотность электрического заряда, Q − заряд, V, v, η − объем, удельный объем, плотность мировой среды соответственно.

Из (3.24) следует, что заряд связан с изменением плотности мировой среды. При заряжании тел, при добавлении в тело, например, одного электрона вокруг тела изменяется электрическое поле (напряженность, электрический потенциал), то есть вокруг тела, по Максвеллу, возникают напряжения в мировой среде. Причиной напряжений являются изменившиеся параметры мировой среды внутри тела: объема, удельного объема, плотности.

В чем заключается природа, сущность отрицательного и положительного зарядов? Избыток электронов внутри тела приводит к увеличению плотности мировой среды, что соответствует отрицательному заряду. Недостаток электронов внутри тела приводит к уменьшению плотности мировой среды, что соответствует положительному заряду.

Из наших рассуждений вытекает, что мировая среда − сжимаема. Действительно, выпишем уравнение непрерывности для токов проводимости [13]

                (3.25)

С учетом (3.23) и (3.24) уравнение (3.25) перепишется

                (3.26)

или

                (3.27)

Учитывая, что мировая среда подвижна (в ней возможно электрическое смещение и вращение, в проводниках − поступательное движение), используя переменные Эйлера, заменим в (3.27) частную производную – полной. Окончательно получим уравнение

                (3.28)

представляющее собой уравнение непрерывности для мировой среды.

В переменных Эйлера полная производная расписывается как сумма локальной и конвективной производных [48]

                (3.29)

где ∇ – оператор набла, в декартовой системе координат равный , что позволяет записать уравнение (3.28) также в виде

                (3.30)

В дальнейшем уравнение непрерывности будет использоваться как одно из основных уравнений, описывающих динамические процессы в мировой среде – физическом вакууме.

Выводы:
          1. Количество электричества, измеряемое в современной физике в Кулонах, соответствует объему мировой среды. Поэтому понятие «электрический заряд» является в физике избыточным, усложняющим простые представления. У элементарной частицы – электрона – нет никакого электрического заряда, а есть объем. Электрический заряд электрона тождественен его объему.
          2. Избыток электронов внутри тела приводит к увеличению плотности мировой среды, что соответствует отрицательному заряду; недостаток электронов внутри тела приводит к уменьшению плотности мировой среды, что соответствует положительному заряду.
          3. Мировая среда– сжимаема.

Глава 4. Уравнения динамики вакуума

Уравнения динамики вакуума представляют собой уравнения электромагнитного поля Максвелла для вакуума, записанные относительно векторного и скалярного потенциалов с учетом возможности перемещения физического вакуума, дополненные уравнением непрерывности и формулой для скорости света. Приведем вывод уравнений. Но прежде чем переходить к выводу, остановимся коротко на некоторых их особенностях.

4.1. Нелинейность уравнений

Уже вскоре после создания специальной теории относительности (СТО), как отмечается в [49], «в конце 1908–1909 г. Эйнштейн... думал о нелинейном и неоднородном обобщении максвелловских уравнений». Значительный прогресс в нелинейном обобщении уравнений электродинамики был достигнут в работах Г. Ми [49, 50] и затем в работах Борна, Инфельда и др. [49, 50, 51]. Но существенных конечных результатов на этом пути в цитируемых работах получено не было, так как в основе их построений лежали идеи СТО, требующие от уравнений инвариантности относительно преобразований Лоренца. Как показано в [4, 5], преобразования Лоренца сохраняют инвариантными линеаризованные исходные уравнения. Не случайно в СТО [14] за основу берутся уравнения Максвелла для покоящихся сред. У Максвелла эти уравнения более общие, и они содержат нелинейные члены.

Большой успех СТО объясняется тем, что в теории относительности был найден единственно верный формально – математический подход, который, беря за основу линейные уравнения для покоящихся сред и привлекая преобразования Лоренца, позволяет получить в некоторых частных случаях верные решения. Но недостатком такого подхода является утрата нелинейных членов в уравнениях. Если привлекать метод аналогий, то нынешнее положение в электродинамике движущихся сред аналогично тому, как если бы мы попытались всю механику жидкости и газа описывать линейными уравнениями акустики. Мир нелинеен. Попытка описать нелинейный мир линейными уравнениями приводит к искажению реальных связей природы.

Поэтому необходимо отказаться от преобразований Лоренца и записать уравнения таким образом, чтобы в них учитывались нелинейные члены, обусловленные возможностью перемещения мировой среды. Учитывая выражение для полной производной в переменных Эйлера (3.29), вторая полная производная определится

                (4.1)

Если рассматриваются линейные уравнения и не учитывается возможность перемещения среды, то полная производная заменяется локальной производной по времени.

Следует отметить, что в последнее время произошло осознание необходимости введения в уравнения электродинамики вместо локальной производной по времени полной, учитывающей и конвективную производную, связанную с перемещением среды [52, 53].

Мы проведем вывод уравнений для неподвижной среды, но на конечном этапе вывода, чтобы учесть возможность перемещения среды, заменим локальную производную по времени полной производной.

4.2. Векторный и скалярный потенциалы

Максвелл при записи уравнений электродинамики широко использовал векторный A и скалярный φ потенциалы [13]. Более широкое признание получила форма записи уравнений электродинамики в переменных напряженностей E и H, данная Герцем и Хевисайдом. Но как справедливо отмечается в [54]: «...векторный потенциал A (наряду с сопровождающим его скалярным потенциалом φ), по-видимому, приводит к более прямому описанию физических процессов. ...В общей теории − квантовой электродинамике − в системе уравнений, заменяющих собой уравнения Максвелла, векторные и скалярные потенциалы уже считаются фундаментальными величинами. Векторы E и B постепенно исчезают из современной записи физических законов: их вытесняют A и φ ».

Это становится тем более актуальным после "материализации" векторного потенциала A Максвелла, который в нашем рассмотрении определяется (3.13) как A = Vη. Учитывая вышеизложенное, уравнения динамики вакуума запишем относительно векторного и скалярного потенциалов.

4.3. Основная система уравнений

Приведем вывод уравнений динамики вакуума. Выпишем уравнения Максвелла для вакуума, записанные в форме Герца-Хевисайда [55]

где Е − напряжённость электрического поля, В − магнитная индукция, Н − напряжённость магнитного поля, D − электрическое смещение, ε – диэлектрическая проницаемость, для вакуума равная единице; ε₀ − электрическая постоянная, равная 0,885 · 10 ^–11 Ф/м ; µ − магнитная проницаемость, для вакуума равная единице; µ₀ − магнитная постоянная, равная 1,26 · 10 ^–6 Гн/м.

Магнитную индукцию, как и у Максвелла [13], определим через векторный потенциал

B = rot A ,                 (4.8)

принимая во внимание, что, согласно (3.13), векторный потенциал равен

A = ηV ,                 (4.9)

где η = m_e/e, V − вектор скорости движения мировой среды.

Подставим (4.8) в уравнение (4.2)

                (4.10)

После преобразований получим

                (4.11)

где φ − скалярный электрический потенциал.

Подставим (4.8) и (4.11), с учётом (4.6) и (4.7), в (4.4). После преобразований получим

                (4.12)

Оператор rot rot преобразуется [48]

                (4.13)

∇² − лапласиан векторного потенциала A.

Подставим (4.13) в (4.12), получим

                (4.14)

Перепишем два последних члена в правой части (4.15) в виде

                (4.15)

Учитывая, что скорость света c определяется как [55]

                (4.16)

выражение в скобках (4.15) равно нулю и представляет собой условие калибровки Лоренца [56]

                (4.17)

С учетом (4.16) и (4.17), уравнение (4.14) перепишется

                (4.18)

Получим уравнение для скалярного электрического потенциала. Подставим (4.11), с учётом (4.6), в (4.5)

                (4.19)

Оператор div grad φ [48]

                (4.20)

∇² − лапласиан скалярного потенциала φ.

Из (4.17) найдём

                (4.21)

Подставим (4.20) и (4.21) в (4.19), тогда

                (4.22)

Сравнивая уравнение непрерывности (3.30) с условием калибровки Лоренца (4.17), с учетом (4.9) получим формулу для скорости света

                (4.23)

Выпишем основные уравнения (4.18), (4.22), (3.28), (4.23), принимая во внимание (4.9). Учитывая, что мировая среда подвижна, в уравнениях (4.18) и (4.22) заменим частные вторые производные по времени − полными. В результате окончательно получим уравнения динамики вакуума

                (4.24)

В этой системе из шести дифференциальных уравнений (первое векторное уравнение представляет собой три скалярных) неизвестных 6 величин −

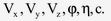
Полные производные в (4.24) содержат нелинейные члены и расписываются

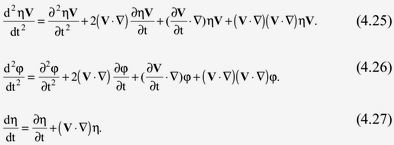
Первое уравнение системы (4.24) описывает распространение поперечных волн в мировой среде − физическом вакууме. Второе уравнение описывает продольные волны напряжения. Третье уравнение системы (4.24) представляет собой уравнение непрерывности мировой среды − физического вакуума. Четвертое уравнение определяет скорость света в мировой среде как скорость распространения возмущений.

Система уравнений (4.24) допускает две системы размерностей.

Первая – электродинамическая система размерностей:

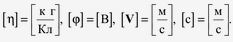
Вторая – механическая система размерностей:

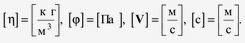
Эти две системы размерностей эквивалентны и пересчитываются с помощью множителя k_Q (3.20). Действительно, заряд в 1 Кл соответствует объему мировой среды в м³

1 Кл = k_Q м³ = 2,34 · 10 ^–28 м³                 (4.28)

Тогда

                (4.29)

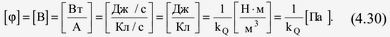
Соотношение (4.30) устанавливает связь между электрическим потенциалом, выраженным в Вольтах, и механическим напряжением, выраженным в Паскалях.

Физический вакуум – сжимаемая среда. Найдём, по аналогии с гидродинамикой [57], коэффициент сжимаемости β_φ и модуль упругости G мировой среды – физического вакуума

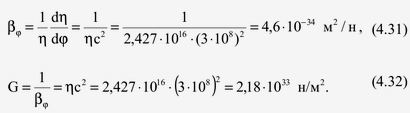
Для сравнения приведём [43] коэффициент сжимаемости 4,7 · 10 ^–10 м²/H и модуль упругости 2,13 · 10⁹ H/м² воды.

Таким образом, сжимаемость мировой среды (физического вакуума) значительно меньше сжимаемости воды, и в некоторых случаях ее допустимо приближенно рассматривать как несжимаемую.

Уравнения динамики вакуума (4.24) являются исходными и включают в себя уравнения механики и электродинамики, закон всемирного тяготения, уравнение Шредингера и др.

4.4. Вспомогательное уравнение

За материалом этого подраздела обращайтесь на

Персональный сайт С.С. Воронкова

Глава 5. Механика – основные законы

В этой главе рассмотрим законы классической механики и покажем, что они выводятся из уравнений динамики вакуума (4.24) при определенных допущениях. Покажем, что из уравнений динамики вакуума следует релятивистская зависимость массы тела от скорости. Проведем вывод закона тяготения Ньютона из уравнений динамики вакуума. Также рассмотрим природу сил инерции и возможность перемещения тел под действием сил инерции.

5.1. Масса и второй закон Ньютона

На обыденном уровне восприятия мира массу можно определить как меру количества вещества. Масса в переводе с латинского означает глыба, ком, кусок. В классической механике Ньютон [25] вводит понятие массы как меры инертности, входящую, как коэффициент, во второй закон Ньютона – «инертная масса», а также массу, как меру тяготения, входящую в закон всемирного тяготения – «гравитационная масса». Экспериментально доказано, что инертная и гравитационная массы, с точностью, определяемой погрешностью эксперимента, равны.

В релятивистской механике инертная масса зависит от скорости

                (5.1)

где m₀ − масса покоя, β = v/c, v − скорость тела, c − скорость света в вакууме.

Но возникает вопрос: если инертная масса в релятивистской механике изменяется согласно закону (5.1), то по какому закону будет изменяться гравитационная масса и сохраняется ли между ними равенство? Пуанкаре по этому поводу отмечает [59]: «Масса имеет два аспекта: во-первых, это – коэффициент инерции; во-вторых, это – тяготеющая масса, входящая в качестве множителя в формулу ньютонианского тяготения. Если коэффициент инерции не является постоянным, может ли быть постоянной притягивающая масса? Вот вопрос, встающий перед нами». Но окончательного ответа на этот вопрос на сегодня не получено.

Также есть определенное противоречие между определением массы как меры вещества и определением релятивистской массы по формуле (5.1). Если мы принимаем эти два определения массы, то получается зависимость количества вещества от скорости, что противоречит закону сохранения массы.

Как определить понятие массы, привлекая представления о мировой среде, чтобы устранить существующие противоречия? Это определение массы мы дали в параграфе 3.2. Оно следующее:
          − масса – мера взаимодействия вещества с мировой средой (физическим вакуумом).

Все атомы, молекулы, тела «погружены» в мировую среду, состоящую из электронов. Любой нуклон атома, молекулы, тела со всех сторон окружен этой средой. Нуклоны с ней контактируют, взаимодействуют, соприкасаются. Эта среда, с одной стороны, заполняет все пространство, а с другой стороны, является составным элементом всех атомов, молекул, тел, состоящих из нуклонов и электронов. Видимо, в этом и заключалась сложность идентификации, распознавания этой среды – она везде и во всём.

Инерционность тела проявляется как результат взаимодействия с этой средой и определяется уравнениями, описывающими процессы в этой среде. Релятивистские эффекты зависимости массы от скорости объясняются свойствами среды и выводятся из уравнений динамики вакуума. Покажем это,

Рассмотрим движение нейтрона в мировой среде. Получим II закон Ньютона из уравнения (4.41). Сила F, которую необходимо приложить к нейтрону, чтобы изменить его скорость, определится

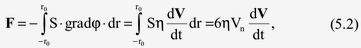
[Вывод опускаю. — О.А.]

5.2. Закон всемирного тяготения

Уравнения динамики вакуума (4.24) включают и гравитационное взаимодействие. Получим закон тяготения Ньютона из вспомогательного уравнения (4.37).

Мировая среда находится в непрерывном движении. Каждой точке мировой среды соответствуют какие-то значения пульсационных составляющих скорости и потенциала. Представим скорость и потенциал как сумму средних и пульсационных составляющих

                (5.18)
Проведем осреднение по времени уравнения (4.37) на интервале T, значительно превышающем период пульсационных составляющих, полагая, что средняя скорость мировой среды равна нулю. В правой части уравнения (4.37) достоверно будет отличен от нуля квадратичный член ...

Анализ выражений (5.27) и (5.28) показывает, что причина тяготения заключается в непрерывных пульсационных колебаниях мировой среды.

Силы инерции отличаются от сил взаимодействия (контактных, упругих, гравитационных и др.), так как для них нельзя указать, со стороны каких тел они действуют. Поэтому считается, что на силы инерции не распространяется третий закон Ньютона. По этой причине в некоторых работах [61, 62] их относят к «псевдо», «нереальным», «фиктивным» силам. Характерной особенностью сил инерции является пропорциональность их, также как и сил тяготения, массе тела.

Но проблема обнаружения тел, со стороны которых действуют силы инерции, существует только в том случае, если мы не учитываем мировой среды, заполняющей все пространство. В нашем представлении масса тела есть мера взаимодействия тела с мировой средой. Пропорциональность сил инерции массе тела свидетельствует о том, что они действуют на тело со стороны мировой среды.

Изложенное позволяет следующим образом определить силы инерции: силы инерции представляют собой силы, действующие на тело со стороны мировой среды (физического вакуума) при ее ускорении.

Второй закон Ньютона выполняется в инерциальных системах отсчета. В неинерциальных системах отсчета для пользования вторым законом Ньютона в него необходимо ввести дополнительно переносные и кориолисовы силы инерции. Этот прием выглядит искусственно. Желательно так записать второй закон Ньютона, чтобы силы инерции появлялись в нем естественным образом, как следствие присутствия мировой среды.

Для первого знакомства достаточно.
Именно данной книги издания 2014 года на
Персональном сайте С.С. Воронкова
пока еще нет, но там имеется
книга 2008 года и другие материалы.

Воронков на профсоюзном митинге отстаивает права преподавателей вузов