Методология аэродинамических
исследований Н.П. КастеринаА.А. Соловьев
Sо1оviev А.А. Methodology of aerodynamical researches by N.P. Kasterin. The little known Kasterin's method is discussed in detail. A review of further researches is presented, 1981.
Исследования, в которых преследуется цель установить единые принципы, управляющие различными физическими явлениями, неизменно привлекают к себе внимание. Развитие концепций, выявляющих взаимосвязь механических, тепловых, электрических и других явлений, происходит, как правило, в острой философской борьбе и сопровождается крайними, полярными оценками, затрудняющими выделение достоинств обсуждаемых теорий. Отрицательные заключения зачастую связываются с выявлением в теории того или иного варианта сведения всех закономерностей к комплексу чисто механических понятий. Получившие такую оценку исследования слабо освещаются в научных изданиях, а по прошествии некоторого времени и вовсе забываются. С точки зрения методологии науки следует периодически проводить детальное обсуждение забытых работ. Стремление глубже рассмотреть те теории, которые, согласно установившемуся мнению, не принесли сколь-нибудь нового и перспективного в понимании сущности изучаемых явлений не есть порок; скорее всего это стимул к открытию новых истин. Ибо в тех теориях, которые в силу тех или иных обстоятельств не решили стоявших перед ними проблем, тем не менее зачастую при внимательном повторном рассмотрении выявлялись интересные физические результаты и методологические приемы. «Как дерево, — писал А. Швейцер, — из года в год приносит одни и те же, но каждый раз новые плоды, так и все идеи, имеющие непреходящую ценность, должны вновь и вновь рождаться в мысль» [1]. И по-видимому, не последнее место в этом принадлежит детальному разъяснению трудно воспринимаемых положений, выявлению их значимости и дальнейшему распространению.
Из истории науки можно привести не один пример того, как судьба одних концепций оказывалась более счастливой, чем другие. Так, первоначально неудачно складывалась судьба уравнений Дж. Максвелла. Его работы были совершенно непонятны современникам, несмотря на громадный авторитет, которым он пользовался как крупнейший ученый своего времени. После признания максвелловской теории стремление конкретизировать передачу электромагнитных действий утратило свою актуальность. Между тем Дж. Дж. Томсон, начиная с 1892 г. и до конца своей жизни, без общего признания пользовался приемом изучения движения силовых трубок (фарадеевых). В его работах наряду со спорными положениями есть ряд интересных в методологическом отношении приемов учета роли среды при описании явлений различной физической природы.
Дальнейшие шаги в развитии представлений Дж. Дж. Томсона были предприняты в исследованиях талантливого русского ученого Н. П. Кастерина (1869—1947) *.
{* Краткий очерк жизни и обзор научных работ Н. П. Кастерина дан в статье Г. М. Теплякова Николай Петрович Кастерин (История и методология естественных наук, вып. 10, 1971, с. 150)}.Им была сделана попытка уточнить уравнения электродинамики и аэродинамики с учетом разрывов непрерывности в силовых линиях соответствующих полей. Для получения обобщенных уравнений аэродинамики и электродинамики им использовался принцип наименьшего действия. Попытка вывести законы электродинамики и аэродинамики из общих принципов механики с использованием допущений о эфире, которые представлялись нелогичными с точки зрения принятых представлений, вызывала суровую и справедливую критику его работ. Развитие современных экспериментальных исследований (в особенности это относится к аэродинамическим явлениям) вновь поднимает на повестку дня те вопросы, которые служили для Кастерина мотивом к уточнению уравнений. Поэтому упомянутые работы Кастерина представляют несомненный методологический интерес. Теперь, когда прошло некоторое время после появления его работ и критических рецензий, можно сделать спокойный анализ имеющихся недомолвок и деталей не только с точки зрения критики, но и с позиции выявления положительного и интересного в методологическом отношении.
Работа Кастерина «Обобщение основных уравнений аэродинамики и электродинамики» была опубликована в кратком виде в качестве предварительного сообщения [2]. Рукопись, содержащая подробное изложение работы, не была напечатана. Научная общественность, таким образом, не имела возможности подробно ознакомиться с идеями Кастерина и получить представление о перспективности и значимости развиваемых им воззрений. Используя предварительное сообщение, рукопись с примечаниями А. К. Тимирязева и материалы из архива, рассмотрим методологию представлений Кастерина по обобщению уравнений аэродинамики, а .также применение и дальнейшее развитие его идей в работах советских исследователей.
1. Метод исключения координат и
представления о скрытых движенияхВ качестве основного метода Кастерин использует метод составления уравнений Лагранжа, обобщенный для физических систем Гельмгольцем в его работах по принципу наименьшего действия [3, 4]. Как известно, Гельмгольц предлагал расширить область применения принципа наименьшего действия за границы механики. Всякое физическое явление при подходящем выборе лангранжиана может быть выражено, согласно его представлениям, в форме принципа наименьшего действия и, следовательно, в форме уравнений Лагранжа. Таким образом, принципу наименьшего действия придается универсальный характер и предлагается им пользоваться для того, чтобы выявлять новые законы физических явлений. Он писал: «...мне кажется, что всеобщая применимости принципа наименьшего действия простирается так далеко, что он может иметь высокую ценность как эвристический принцип и как проводник для попыток формулировать законы новых классов явлений» [4].
Для того чтобы расширить возможности принципа наименьшего действия, Кастерин использует представление о скрытых или циклических движениях. Понятие о циклических системах было введена Томсоном и Тэтом [5] и получило дальнейшее развитие у Гельмгольца [6] и Герца [7].
Если записать выражение для энергии системы:
(1)
то можно дать следующее определение циклической координаты. Циклической называется такая координата, которая входит в выражение для энергии своей первой производной по времени. Циклической системой называется такая система, энергия которой может быть представлена с достаточной степенью точности в виде однородной функции второй степени от скорости изменения циклических координат. Математически условие того, что qa — циклическая координата, записывается так:
(2)
Например, угол вращения будет циклической координатой, проявляющейся только в соответствующем импульсе вращения. Так, вращающийся шар, заключенный в непроницаемую оболочку, вносит затруднение попыткам привести движущуюся оболочку в обратное движение путем обращения наблюдаемой скорости. Необычное поведение оболочки связано со скрытым в ней внутренним движением шара. В подобных случаях, когда невозможно оказать внешнее воздействие на вращение оболочки, импульсы, соответствующие циклическим координатам, постоянны, т.е.
(3)
Откуда
(4)
где pa — постоянные неизменяющиеся моменты циклического движения. Соотношение (4) дает основание для использования приема, введенного Раусом [8] и впоследствии Гельмгольцем [6]. Этот прием получил название метода игнорации циклических координат.
Выражения (4) приводят к уравнениям, при помощи которых
можно выразить как линейные функции параметров
:
(5)
Путем подстановки (5) в функцию Лагранжа величина
исключается из него. В лагранжиан L теперь входят лишь
и постоянные pa. Обозначим измененное значение лагранжиана L через L*. Для производных от L* по qb и
будем иметь:
(6)
(7)
С учетом выражения (4) последние равенства могут быть переписаны так:
(8)
(9)
Итак, вместо лагранжевой функции мы имеем функцию:
(10)
Вместо уравнения Лагранжа
(11)
мы получим
(12)
где j =1, 2, 3 .... Раус назвал функцию R измененной функцией Лагранжа, а Гельмгольц обозначил через Н = —R функцию, которую назвал кинетическим потенциалом. Циклические системы обладают двумя важными особенностями.
1. Функция R включает в себя члены, линейные по отношению к скоростям. Таких членов не было в первоначальном выражении для кинетического потенциала.
2. Функция R содержит члены, которые представляют собой однородную квадратичную форму относительно постоянной pa с коэффициентом, зависящим только от параметра qb. В уравнении (12) эти члены в производной ∂R / ∂qj выражают потенциальную энергию, эквивалентную кинетической энергии циклических или скрытых движений.
Отмеченные две особенности циклических систем оказали очень существенное влияние на возможность обобщения принципа наименьшего действия для физических систем. Путем игнорации циклических координат физическая система с существующими в ней взаимодействиями может быть представлена в виде системы, содержащей частицы, находящиеся в видимом и скрытом движении. При этом величины, проявляющиеся как потенциальные энергии, можно рассматривать как кинетические энергии циклических или скрытых движений. Кинетическая энергия не обязательно имеет вцд квадратичной функции скоростей. При исключении части координат для остающихся она приобретает линейную зависимость от соответствующих скоростей.
Таким образом, системы со скрытыми движениями расширяют сферу применения принципа наименьшего действия для физических систем с различными взаимодействиями. В самом общем виде можно считать, что для физической системы с взаимодействием между частицами можно найти значение кинетического потенциала и составить (уравнение движения. Разнообразные силовые взаимодействия, существенно влияющие на динамическое поведение системы, при этом могут интерпретироваться как силы, происходящие от внутренних движений. В механике Герца мысль о том, что всякую энергию можно рассматривать с кинетической точки зрения, видна наиболее отчетливо. Комментируя ее, Гельмгольц писал в предисловии к немецкому изданию механики: «... надо принимать гипотезу о существовании большого числа невидимых масс и незамечаемых движений, чтобы ими объяснить силы, действующие между телами, не находящимися в непосредственном соприкосновении».
Идея циклических или скрытых движений и универсальности принципа наименьшего действия проникала в исследования физических явлений с трудом [11—13]. Основная причина этого заключалась в том, что усматривался субъективный смысл в приеме разделения движений на внешние (видимые) и внутренние (скрытые) как пути универсализации механических принципов. Интенсивное развитие электродинамики и теории атома привело к тому, что направление Гельмгольца оказалось в стороне от тех путей, по которым развивалась физическая наука.
2. Прием введения в уравнения
движения разрывных решенийВ попытках сформулировать уравнения электродинамики и аэродинамики в рамках принципа наименьшего действия возникали два вопроса. Во-первых, необходимо было определить элемент прерывности. Во-вторых, найти способ синтеза прерывностей с непрерывностями.
Следует заметить, что решение первого вопроса в рамках механических представлений затрагивало проблему конкретизации передачу силового действия. Выдвигаемые на этот счет мыслимые образы изолированных физических элементов прерывности были связаны с представлениями об эфире.
Кастерин в своей работе, принимая точку зрения о фарадеевой трубке как носителе взаимодействий, получает очень важный результат. Показывая формальную осуществимость применения принципа наименьшего действия как к электродинамическим, так и аэродинамическим явлениям, он устанавливает причины неудач механистических попыток построить модель эфира.
Взяв за исходную модель представление о фарадеевой силовой трубке, Кастерин обнаруживает особенность в поведении электромагнитных систем с введением в выражение для энергии трубки энергии, связанной с ее продольным движением. До него принималась в расчет только энергия поперечного движения трубки. Н. Е. Жуковский в своей речи «Старая механика в новой физике» так пишет об этом дополнении Кастерина: «Вывод уравнений Максвелла, в указанной классической форме сделан проф. Н. П. Кастериным. С разрешения автора я закончу свою речь указанием на идею этого вывода. Первая группа уравнений Максвелла, оказывается, выражает неизменность трубок Фарадея, вполне аналогичную закону сохранения вихрей в гидродинамике несжимаемой жидкости, причем роль вихревых линий играют линии электрических сил, роль напряжения вихря—элементарный заряд электрических сил и роль скорости — скорость смещения эфира. Если рассматривать систему трубок Фарадея и составить полную энергию по известной формуле энергии электромагнитного поля, то начало Гамильтона дает вторую группу уравнений Максвелла, выражающую производную по времени от магнитных сил, с некоторым обобщением, приводящим к обыкновенным уравнениям Максвелла при перпендикулярности смещений к направлению электрических сил. Не является ли аналогия трубок Фарадея с вихрями несжимаемой жидкости указанием того пути, следуя которому, можно построить механику эфира, и действительно ли утратилась роль «старой механики» в новой физике?» [12].
Из приведенной цитаты видно, что Н. Е. Жуковский с пониманием отнесся к идее уточнения уравнений электродинамики. Более того, он способом, отличным от Кастерина, получил уравнения, в точности совпадающие с теми, что найдены Кастериным. К сожалению, первоначальный замысел опубликовать этот вывод в 9-м томе собраний сочинений Н. Е. Жуковского не осуществился.
С введением элементов прерывностей в виде силовых фарадеевых трубок возникала новая задача. А именно, необходимо было сформулировать прием перехода от прерывных трубок к непрерывным величинам. Соответствующего аппарата для оперирования с разрывными функциями не было. Кастерин применил операцию сглаживания разрывных функций. Для этого он полагает, что в центрах трубок скорости движения — постоянные величины, а скачок скорости при переходе от трубки к другой аппроксимируется системой гладких функций, касающихся к отрезкам прямой в центре трубки. Аппроксимирующая кривая имеет точки перегиба на границах трубок. Условие касания кривой к отрезкам прямой выражается через равенство нулю соответствующих производных.
Отметим, что введение представлений о замене непрерывного множества силовых фарадеевых линий дискретными и попытка построить на этой основе картину электромагнитных явлений выдвигались П. Дираком в качестве возможной и плодотворной идеи для решения ряда проблем квантовой электродинамики. В статье «Эволюция физической картины мира» [13] он, в частности, писал: «Если предположить, что эти дискретные силовые фарадеевские линии представляют собой нечто фундаментальное в физике и что на их основе должна строиться вся картина электромагнитного поля, тогда все заряды всегда оказываются по своей величине кратными е». И далее: «Предположим, что эти линии могут двигаться. Некоторые из них, образующие замкнутые петли или просто простирающиеся от минус до плюс бесконечности, будут соответствовать электромагнитным волнам. У других будут концы, и эти концы будут зарядами. Иногда может происходить разрыв силовой линии. Когда это происходит, то появляются два конца, которые должны представлять собой заряды. Такой процесс разрыва силовой линии можно было бы представлять себе как картину рождения пары электрон — позитрон. Подобная картина вполне разумна и если бы ее удалось разработать, то это дало бы теорию, в которой заряд е входил бы в качестве фундаментальной величины. Я не смог пока найти какой-либо системы уравнений движения этих силовых линий, и эту идею я выдвигаю просто в качестве возможного физического образа» [13].
Соображения, приведенные в цитированном высказывании Дирака 1963 г., по существу говоря, в определенном варианте были реализованы Кастериным в 1937 г. Вот слова, которые он высказывает в качестве заключения в своем докладе после разбора случая движения изолированной фарадеевой трубки: «Сравнивая решения, полученные для электрона (позитрона) и протона мы можем предсказать, что если удастся на опыте при помощи внешнего магнитного поля увеличить скорость вращения позитрона в 919 раз, то он превратится в протон, а из электрона таким же путем должен получиться антипротон, еще не бывший в руках физико-экспериментаторов».
В свете высказанных суждений, по-видимому, не следует категорически относить стремление Кастерина ввести разрывы непрерывности в силовые линии только для того, чтобы показать несостоятельность теоретических основ современной физики. Скорее это попытки всесторонне рассмотреть роль среды.
3. Уравнения аэродинамики
Уравнения аэродинамики получены Кастериным для среды вихревой структуры, которая состоит из отдельных вихревых трубок. Движение жидкости в течении бесконечно малого промежутка времени представляется в виде течения струек внутри трубкообразных поверхностей. Заметим, что указанный способ интерпретации течения с успехом применялся Н. Е. Жуковским в его магистерской диссертации. Кастерин использует прием выделения вихревых трубок в качестве элементарной ячейки фактически для того, чтобы дать геометрическую интерпретацию идеи о разрыве линейной скорости потока жидкости. В самом деле, для двух рядом расположенных вихревых трубок в точке их соприкосновения линейная скорость будет испытывать резкие изменения. Чтобы описать разрывной характер изменения скорости при переходе от одной вихревой трубки к другой, Кастерин прибегает к конечно-разностному представлению гидродинамической скорости. Для этого он разбивает массу газа соответствующими координатными поверхностями так, чтобы каждая ячейка представляла собой «аэродинамическую частицу». По смыслу «аэродинамическая частица» эквивалентная физически бесконечно малому объему.
Рис. 1. Схема "аэродинамических ячеек"
На рис. 1 схематически показана координатная сетка на поверхности
. За оси координат Н. П. Кастерин выбирает криволинейные ортогональные координаты λ, μ, ν. Направление λ определяется направлением вектора угловой скорости вращения ячейки; направление ν — направлением составляющей скорости w, нррмальной к вектору угловой скорости ячейки; координата μ направлена перпендикулярно к направлению (λ, ν) и составляет с ними правую систему координат, причем
— коэффициенты Ламе.
Вихревые ячейки, соответствующие узлам трубок, нумеруются индексами а, а + 1, а + 2, ...; b, b + 1, b + 2, ...; c, c + 1, c + 2, ... Если Ωλ — угловая скорость вихревой трубки, то
(1)
Чтобы выразить уравнения движения завихренного газа в форме Лагранжа — Гельмгольца, Н. П. Кастерин составляет кинетический потенциал элементарной ячейки. Кинетическую энергию он выражает в виде суммы кинетической энергии E1 молекулярных движений газа в вихревой трубке и кинетической энергии E2 поступательного движения трубки. Причем
(2)
здесь γ = cp/cv — адиабатная константа, m0 — масса газа в ячейке (a, b, c), C0 — ньютоновская скорость звука. Эту энергию он преобразует к виду:
(3)
Здесь ρ0 — плотность газа в ячейке. При этом средняя плотность ρ0 определяется соотношением:
(4)
где
(5)
Кастерин предполагает, что масса газа в ячейке и, следовательно, плотность распределяются по закону Больцмана:
Используя последнее соотношение, можно написать для массы газа в ячейке (abc)
Интегрируем последнее выражение, принимая во внимание, что v = Ωλ и
;
в результате получаем
Но g может быть записано в виде
(6)
Тогда
(7)
Поскольку объем аэродинамической частицы по определению равен
(8)
то вместо выражения (7) можно написать формулу (4). Что касается перехода от формулы (2) к (3), то заметим, что для
величина
С учетом этого можно написать
Но согласно (4):
откуда
что объясняет формулу (3).
Кинетическая энергия, связанная с поступательным и вращательным движением трубки, записывается Кастериным в форме
(9)
Последний член им преобразуется к такому виду:
(10)
Вычислим интеграл I и покажем справедливость формулы (10):
Учитывая соотношения (6) – (8), находим
(11)
Последнюю формулу можно тождественно переписать так:
В свою очередь это соотношение может быть представлено в виде
или
Если взять среднее арифметическое от двух последних формул, то мы получим выражение интеграла I в форме (10).
Таким образом, кинетическая энергия, по Кастерину, состоит из кинетической энергии молекулярных движений
кинетической энергии поступательного движения трубок
и кинетической энергии вращательного движения трубки с угловой скоростью Ωλ
При анализе последнего выражения следует иметь в виду соотношение (5). Для системы вихревых трубок с учетом составленного выражения кинетической энергии лагранжиан имеет вид
Так как λ не входит в это выражение, и есть лишь зависимость от λ, (u = h1λ), то параметр λ — циклический. Так же как и в случае электродинамики исключаем циклическую координату. Измененный лагранжиан будет отличаться от данного тем, что у члена, содержащего w², знак изменится на противоположный:

(12)
Преобразуем (12), имея в виду соотношения:
Тогда получаем
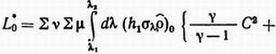

Так как
(13)
то приходим к следующему выражению для лагранжиана, которое используется Кастериным при получении уравнений аэродинамики
(14)
Если считать g << 1, то
Лагранжиан с точностью до величин порядка g² принимает вид
(15)
Подставляем (15) в уравнение Лагранжа и дифференцируем по параметрам с индексами
Так же окак в электродинамике, имея в виду, что сумма содержит члены с индексами
после разложения
в ряд с точностью до членов высшего порядка малости получаем:
Из общего выражения для
интеграл исключается, так как
. Поэтому в сооeветствии с уравнением Лагранжа, находим
 (16)
(16)
Чтобы преобразовать это выражение, принимаем во внимание, что при g << 1, уравнение движения дает
(17)
и поэтому (16) может быть записано так:
(18)
В соответствии с формулой (5) при условии, что напряжение вихря QxOx сохраняется, имеем
(19)
в соотношении
Тогда формула (18) принимает вид
Дифференцирование по параметру v0 в соответствии с тем, что лагранжиан зависит от
дает уравнение Лагранжа в полном виде. В результате получаем
(21)
К уравнениям (20) и (21) Кастерин, так же как в электродинамике, присоединяет уравнение связи между трубками. Фактически это уравнение постулируется. С помощью его выражается предположение о том, что энергия частицы изменяется лишь при движении вдоль координаты ν и остается неизменной при перемещении частицы в направлении координаты μ:
(22)
В соответствии с уравнением (20)
(23)
Подставляя (23) в (22) получаем
(24)
В уравнения (20), (21), (24) входят производные по параметрам с индексами. Указанные уравнения определяют деформацию и движение в вихревом поле в зависимости от координат и скоростей в узловых точках трубок. Эти узлы, замечает Кастерин, не могут быть сближены как угодно близко, и необходимо учитывать факт прерывности вихревого поля. Чтобы учесть конечность размера «аэродинамической частицы», Кастерин использует тот же прием, что и в электродинамике. Скачок функции аппроксимируется системой гладких функций, касающихся к отрезкам прямой в узлах сетки. Дифференцирование по параметрам с индексами принимается тождественно равным дифференцированию при постоянной скорости
(оно обозначается символом δ).
Продифференцируем уравнение связи (24)
Далее имеем

По обычным правилам дифференцирования имеем
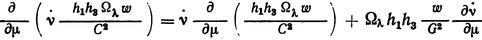
Так как
в соответствии с условиями сглаживания, то
и, следовательно, (24) приобретает вид
Умножим обе часта последнего уравнения на
и учитываем, что
, тогда
(25)
Аналогично преобразуется уравнение (20), так как
и вследствие условий сглаживания
получаем
(26)
Теперь сделаем некоторые преобразования с производной по времени уравнения (21):
Это преобразование возможно, так как
Учтем далее, что
, и получим
(27)
Преобразуя первый член (21) от производной по параметрам к производной по координате, так же как и ранее находим
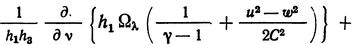
(28)
К полученным уравнениям (24), (25), (28) Кастерин добавляет условие, определяющее вихрь:
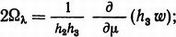


При условии постоянства Ωλ в пределах элементарной вихревой трубки из приведенных выражений следует уравнение непрерывности вихря по его длине:
(29)
Что касается уравнения, описывающего сохранение напряжения вихря, то Кастерин показывает, что оно лишь для случая γ = 2 имеет известный вид:
(30)
Вывод, сделанный Кастериным, имеет очень важное значение для оценки реальных явлений. Для реальных газов всегда вихревые образования являются неустойчивыми. Вместе с этим оказывается, что при определенных условиях в реальных явлениях под действием внешних воздействий возможно образование вихревого движения. В кратком докладе Кастерин дает лишь указание на этот счет и не приводит конкретных соотношений. Покажем, как их можно получить. Для этого составим дифференциальное уравнение движения для Ωλ
(индексацию, отмечающую элементарную ячейку, опускаем). Причем
Лагранжиан для одной аэродинамической частицы принимаем таким:
(31)
Вычислим вначале производную
. Будем иметь в виду соотношение, которое легко получить:
(32)
где
(33)
Тогда
(34)
Из выражения (32) находим
(35)
Выражение (32) можно преобразовать, если обозначить
(36)
(37)
Теперь уравнение Лагранжа представляет следующее:
(38)
Отсюда следует, что только при γ = 2 (см. (31)) мы получаем сохранение напряжения вихря, т. е. уравнение вида (30), при этом предполагается, что
Интегрируя (38) по времени, можно получить напряжение вихря как функцию его угловой скорости. Можно показать, что эта функция имеет максимум для случая γ < 2. Для газа с адиабатным коэффициентом γ = 2 уравнения аэродинамики оказываются тождественными с уравнениями электродинамики.
Кастерин подчеркивает параллелизм двух систем основных уравнений.
Сравнение двух систем уравнений приводит Кастерина к следующему заключению. Газ с адиабатным коэффициентом γ = 2 или, согласно его терминологии, «сверхгаз» приводит к уравнениям, по форме соответствующим уравнениям электродинамики. Подчеркивая нереальность «сверхгаза» в отличии от известных нам газов, для которых γ < 1,6, Кастерин совершенно справедливо отмечал несостоятельность попыток обосновать представления об эфире. Вместе с этим, используя аналогию «сверхгаза» и эфира, он пытался сделать далеко идущие обобщения и свести некоторые характеристики электромагнитного поля к чисто механическим величинам, что вызвало в свое время у ряда ученых резкие замечания.
Уравнения движения, записанные для чисто вихревого потока «сверхгаза», носят абстрактный характер и не могут быть использованы при описании конкретных течений. Желая проиллюстрировать плодотворность развиваемого им подхода, Кастерин получает уравнение движения для конкретного типа потока. Он рассматривает потенциальное течение за границей твердого вращения бесконечно длинного вихревого столба газа. В этом случае в лагранжиан не включается энергия вращения. Все рассуждения, как и ранее, проводятся в криволинейной системе координат λ, μ, ν, причем
(41)
Уравнения движения в форме Эйлера в этом случае могут быть в выбранной системе координат записаны в следующем виде:
(42)
Обобщенные уравнения аэродинамики, полученные из уравнений Лагранжа, Кастерин «представляет, используя сглаживание разрывных функций. С этой целью, как уже указывалось, используются операции δ/δλ, δ/δμ, δ/δν, которые означают, что соответствующие производные берутся в предположении неизменности величин
. Полученные уравнения имеют вид
(43)
В развернутом виде они могут быть записаны так:
(44)
Для безвихревого движения имеем
(45)
Теперь можно упростить уравнения (44). В самом деле, так как u = h1λ то
и
Но в силу (45)
, поэтому
(46)
Аналогично осуществляется преобразование по другим координатам. Кроме того, «в соответствии с формулами (45) имеем
В результате получаем из (44) следующую систему уравнений:
(47)
Сравнивая (47) и (42), видим, что вся разница сводится к изменению знака у членов
Недостатком уравнений (47) является отсутствие предельного перехода к уравнениям в форме Эйлера. В полученных впоследствии А. С. Предводителевым уравнениях движения неидеально — сплошной среды этот недостаток устраняется [21].
4. Дальнейшее развитие аэродинамических
представлений Н.П. КастеринаПоставленная Кастериным задача анализа гипотез, лежащих в основе уравнений аэродинамики, и предполагаемые уточнения представляют интерес в связи с отсутствием удовлетворительных объяснений ряда результатов современных экспериментов. Для существующих теоретических построений таких явлений, как аэродинамика разряженных газов, турбулентность, гидродинамика многофазных систем и вихревых движений, представления Кастерина могут оказаться весьма полезными при устранении возникающих затруднений. Не следует полагать, что концепция Кастерина существенно отличается и перечеркивает другие возможные пути интерпретации указанных явлений. Все они, по сути дела, подчинены одной задаче — отыскать и опробовать различные варианты дополнений и уточнений уравнений движения газа и жидкости. Принимаются поправки на сжимаемость, сдвиговую и объемную вязкости, нелинейность связи скоростей сдвига и напряжений, несимметрию тензора напряжений, разрывов в течении и т. п. По форме вносимые в уравнения движения уточнения обеспечиваются либо изменением динамической части уравнений движения, либо кинематической. Предполагаемые Кастериным уточнения кинематических нелинейных членов уравнений, по-видимому, в ряде случаев оказываются методологически предпочтительнее, чем более распространенный динамический подход. Заметим попутно, что соответствие двух упомянутых способов описания аэродинамических явлений наглядно продемонстрировал О. Рейнольдс в своем замечательном исследовании, посвященном турбулентности [14]. Переход от уравнений Навье — Стокса к уравнениям турбулентности, предложенный им в этой работе, предусматривал преобразование нелинейных членов, определяющих ускорение потока за счет конвективных движений, в компоненты тензора напряжений.
Мы не склонны здесь анализировать достоинства и недостатки различных путей решения стоящих перед аэродинамикой задач. Наша цель проследить основные этапы дальнейшего развития и применение аэродинамических идей Н. П. Кастерина.
Существенный вклад в этом направлении сделан профессором Московского университета А. С. Предводителевым. Ему принадлежит значительное число публикаций, в которых проанализированы гипотезы Н. П. Кастерина, получены уточнения его уравнений и на их основе решен ряд конкретных и практических задач [15—21].
А. С. Предводителев, разъясняя мотивы, побудившие к обобщению уравнений аэродинамики, обращал внимание на важное место, которое занимает в представлениях Н. П. Кастерина идея о разрывном характере течений.
В отличии от Н. П. Кастерина, для того чтобы учесть гидродинамическую неоднородность или неидеальную сплошность среды в уравнениях, он идет более общим путем и обращается к выводу уравнений движения газа, сделанному Максвеллом с молекулярно-кинетических позиций.
Метод Максвелла перехода от дискретности к континууму предусматривает использование той или иной гипотезы о связи переносных скоростей сталкивающихся молекул и гидродинамических скоростей. Различные гипотезы приводят к разным уравнениям движения. Максвелл в предположении, что сталкивающиеся молекулы имеют одинаковую переносную скорость, получает уравнения вязкой жидкости в форме Навье — Стокса. А. С. Предводителев, пользуясь методом Максвелла, в 1948 г. уточнил уравнение Навье — Стокса [15]. Им дано новое определение гидродинамического континуума.
А. С. Предводителев принимает, что переносные скорости сталкивающихся молекул u1i , u2i являются линейной функцией градиента гидродинамической скорости:
(1)
здесь
— координата центра тяжести физически малого объема.
Различие переносных скоростей молекул в физически малом объеме, по которому происходит усреднение скорости движения среды, может оказаться существенным в том случае, когда имеют место разрывы в течении или, реальнее, резкие изменения гидродинамических скоростей на длине свободного пробега молекул. Если освободиться от гипотезы Максвелла о равенстве скоростей u1i = u2i = vi и принять условие (1), то получаются уравнения А. С. Предводителева, названные им уравнениями движения неидеально–сплошной среды:
(2)
Параметр β, пропорциональный множителю А в условии (1), был назван им параметром неидеальной сплошности. Позже в литературе он получил название параметра Предводителева [22, 23].
Параметр может быть как положительным, так и отрицательным в зависимости от соотношения между u1i , u2i . Для одноатомного газа γ = 5/3, и при β = 0 уравнения (2) переходят в уравнения Навье — Стокса. Равенство нулю параметра β означает равенство переносных скоростей сталкивающихся молекул.
При β = 2, μ = 0 уравнения (2) принимают форму, соответствующую той, в которой они были получены Н. П. Кастериным для безвихревого течения [3, 33].
Гипотеза А. С. Предводителева в математическом смысле означает, что разрыв гидродинамической скорости в усредняемом объеме следует аппроксимировать некоторой функцией, пропорциональной градиенту усредненной или гидродинамической скорости. Следовательно, коэффициент β характеризует выбор функции, аппроксимирующей разрыв. Как следствие сглаживания разрывов в левой части уравнений движения появляются члены, определяющие дополнительный вклад в конвективный перенос импульса и сжимаемость.
Дополнительные кинематические члены в уравнениях движения могут быть преобразованы в члены, определяющие гидродинамические напряжения. В работе [24] получены выражения для компонент тензора напряжений в предположении, что скорости сталкивающихся молекул не равны:
 (3)
(3)
Когда переносные скорости u1i = u2i = vi , то (3) переходят в выражение для напряжений, приводящих к уравнениям Навье — Стокса. Если же использовать формулы (3), не принимая определенной гипотезы относительно переносных скоростей сталкивающихся молекул, то можно, как было показано в [24], получить уравнения движения в виде
 (4)
(4)
Если раскрыть в уравнении (4) выражения для произведений переносных скоростей молекул, например в соответствии с гипотезой (1), то нетрудно получить уравнения А. С. Предводителева (2).
Предложенный А. С. Предводителевым прием анализа условий перехода от дискретного к континууму при выводе уравнений движения среды был впоследствии использован А. В. Лыковым и В. А. Бубновым [25] для уточнения уравнений турбулентности О. Рейнольдса. О. Рейнольдс выделял в молярном движении хаотичное и направленное и получил свои уравнения путем усреднения в молярном объеме уравнений Навье — Стокса. При этом он использовал гипотезу, согласно которой средняя скорость моля в объеме усреднения равна средней скорости центра тяжести этого объема. В работе [25] принимается другая гипотеза при усреднении уравнений Навье — Стокса. Средняя скорость любого моля в объеме усреднения полагается равной средней, скорости центра тяжести объема плюс добавок, пропорциональный градиенту гидродинамической скорости. Усреднение уравнений Навье — Стокса по ансамблю молей с помощью указанной гипотезы приводит к уравнениям турбулентности, подправленным на дискретную структуру турбулентного потока.
Появление параметра неидеальной сплошности в уравнениях движения ставит закономерный вопрос: от каких физических величин он зависит?
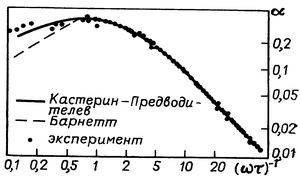
А. С. Предводителев считал, что решать эту задачу нужно экспериментально [17]. Одним из способов определения параметра β может служить явление акустической дисперсии в разреженных газах. В работе «О дисперсии акустических волн в разреженных газах» [17] он использует полученные им уравнения движения для интерпретации поведения коэффициента поглощения в разреженных газах в зависимости от отношения частоты ультразвука к давлению. Сравнение с опытом результатов его расчета позволяет сделать вывод о том, что полученные им уравнения дают лучший результат, чем приближение Барнетта вплоть до чисел Кнудсена порядка единицы. Впоследствии более точный расчет коэффициента поглощения ультразвука α фронтовым методом сделан в работе [26]. В отличии от формулы для коэффициента поглощения А. С. Предводителева получено выражение, в котором учтены члены порядка (ωτ) –1, (ωτ) –2 при переходе от комплексной скорости ультразвука к коэффициенту поглощения ультразвука.
А. С. Предводителев полагает параметр неидеальной сплошности β = 1,5 и получает удовлетворительное совпадение с данными опытов Гринспена до чисел Кп ≈ 1. В работе [26] из условия лучшего совпадения с данными опытов по более точной формуле акустической дисперсии до чисел Кп ≈ 1 найдено в пересчете к значениям А. С. Предводителева, что параметр β = 1,62. На рис. 2 представлены результаты расчета [26] (оплошная линия) для одноатомных газов в уравнении с расчетами Барнетта.
Рис. 2. Акустическая дисперсия в разряженных гахах
Другой пример применения уравнений неидеальной сплошности — задача о движении разреженного газа в трубе. Расчет скорости течения с использованием граничных условий скольжения и учет уравнения состояния и соотношений для температурного скачка приводят А. С. Предводителева к следующей формуле:
(5)
Здесь α1 — постоянная скольжения, α2 — коэффициент температурного скачка. С. И. Грибковой разработана теория метода одновременного измерения температурного скачка и скольжения в условиях таких потоков разреженного газа, когда имеются значительные градиенты температуры и скорости на длине l свободного пути молекул [27—29]. В опытах, проведенных С. И. Грибковой, показано, что когда на средней длине свободного пути молекул перепад температуры порядка 10°С, а перепад скорости — 60 м/с, то осуществляется закон распределения скоростей, соответствующий решению уравнения Больцмана в первом приближении. При этом отношение коэффициентов α1 и α2 равно 8/15. Решение уравнений Навье — Стокса, как было показано А. С. Предводителевым, дает для отношения α1 / α2 = 2. Уточненные уравнения (2) определяют зависимость этого отношения от параметра β (см. формулу (5)).
Если принять для параметра β выражение, предложенное А. С. Предводителевым, т. е. β = (3/2) · Кп · M, то для α1 / α2 = 8/15 параметр β = 0,73. При М = 1 получаем, что d ≈ 2l. Следовательно, для континуального рассмотрения вязкомолекулярных течений на основе уточненных уравнений аэродинамики физически малый объем должен в 8 раз превосходить куб с ребром, равным средней длине свободного пути молекул.
Еще одна возможность испытать уточненные уравнения аэродинамики открывается при интерпретации эффекта Рейнера. Сущность эффекта сводится к тому, что при определенных условиях в пространстве между вращающимися дисками образуется резкий подсос воздуха к центру, который создает своего рода воздушную «подушку». Уравнения Навье — Стокса не описывают этот эффект. В работе [30] проведено решение уравнений А. С. Предводителева для задачи о движении вязкого несжимаемого газа в пространстве между вращающейся неограниченной плоскостью и параллельной ей неподвижной. В результате получена формула для перепада давления вдоль радиуса на неподвижном диске. Перепад давления оказался зависящим от параметра β.
Эксперименты, выполненные сотрудниками ИТМО АН БССР под руководством А. В. Лыкова, показали, что перепад давления при определенных режимах вращения, зазорах и внешнем давлении меняет знак [31]. В работе [30] удалось установить, что параметр
(6)
где μ — динамический коэффициент вязкости, R — радиус дисков, ω — угловая скорость вращения, S — зазор, P0 — внешнее давление. Критическое значение параметра β, при котором перепад давлений меняет знак, оказалось равным 2,5. Заметим, что по данным измерений [32] в ряде жидкостей критическое значение β в пересчете на числовой коэффициент 1,9 · 103 равно β = 1,4.
По инициативе А. С. Предводителева на кафедре молекулярной физики МГУ в 1972 г. начаты исследования вихревых движений. Среда с вихревой структурой является типичным примером неидеально-сплошной среды [38]. Для вихрей наблюдение эффектов, которые свидетельствуют об отклонении от классических решений, может быть достигнуто использованием сравнительно несложных экспериментальных средств. В теоретических и экспериментальных работах Н. П. Кастерина указаны те свойства вихревых трубок, которые предсказываются и могут быть интерпретированы в рамках уточненных уравнений движения [2, 33, 34]. Зона гидродинамической неоднородности и неравновесности, как показывают опыты, образуется в вихревых трубках при сравнительно небольших числах Россби и Рейнольдса в обычных жидкостях и газах. Зона неравновесности определяется характером перехода течения от вихревого к потенциальному. Гидродинамическая неоднородность проявляется с возникновением турбулентных пульсаций.
Анализ элементарного конечно-разностного вывода уравнений аэродинамики, выполненный в работе [35], показывает, каким образом параметр β зависит от зоны неравновесности и размеров аэродинамической частицы. Это выражение имеет следующий вид:
;
Здесь через a обозначен размер Δl / l физически малого объема — «аэродинамической частицы» по отношению к длине свободного пробега молекул l; a = 1 – Δl / l (a ≤ 1). Величина α² определяет относительную ширину Δr / r зоны релаксации от вихревого течения к потенциальному и время восстановления равновесия:
Здесь r — характерный размер в потоке, tm — макроскопическое время, τ — время релаксации.
Если a ≠ 1, то при α²a² > 1 получаем 1 > (1 — β) > 0 и 1 > β > 0. В предельном случае tm > τ и узкой релаксационной зоны с незначительной гидродинамической неоднородностью (a ≈ 1) получаем β = 0 и уравнения движения в классической форме.
Может быть и другой случай, когда при a ≠ 1 произведение α²a² < 1. Здесь имеем 1 < 1 — β < –1, или 1 > β > 2. В пределе, когда tm ≈ τ, при широкой релаксационной зоне и гидродинамической неоднородности уравнения движения принимают форму Кастерина — Предводителева с β = 2.
Для вихревых трубок, как показывают наши наблюдения, параметр α², определенный по размерам зоны перехода от вихревого течения к потенциальному на кривых тангенциальной скорости в воздушных вихревых трубках, может быть близок к единице. В частности, при скорости ядра вихря 10 м/с величина α² ≈ 1,2. Классические решения в этом случае могут иметь место лишь тогда, когда мгновенные скорости турбулентного потока неизменны в пределах относительных размеров аэродинамической частицы: 0,7 < a < 1.
Критерий гидродинамической неоднородности для вихревых трубок, по-видимому, должен зависеть от степени турбулентности потока, структуры внутренних течений и т. п. Предложенная в работе [30] формула (6) для параметра β обладает некоторой универсальностью и, вероятно, может быть, как показали наши опыты [36], использована для расчета характеристик вихрей даже при малых значениях β. Относительный радиус r0 вихревого шнура, возбуждаемый в камере, удалось рассчитать по формуле r0 = (4,9 · 102β)–2/3. Значения параметра β рассчитывались по формуле (6) и в наших опытах изменялись в небольших пределах, имея порядок 10 –2.
Интерпретация кривых давления в вихре при помощи формул, полученных из уравнений Кастерина — Предводителева, дает для параметра β значения порядка 0,5 [37]. Введение в расчеты кривых ΔР(r) этого параметра позволяет в рамках одномерной задачи описать всю кривую, включая и значения вблизи оси вихря. Классическая теория, как известно, дает решения для давления, завышенные на оси по отношению к опыту. Численное различие расчетов параметров β, по данным измерений для давлений и радиусов вихревых трубок в камере, требует, по-видимому, уточнения числового множителя в формуле (6).
Остановимся в заключении на одном эффекте, изучение которого может оказать весьма существенную помощь в понимании тех факторов, которые определяют параметр β. Имеется в виду эффект изменения знака завихренности (ротора скорости).
Экспериментальное исследование этого эффекта, предсказываемое уточненными уравнениями движения, начато Н. П. Кастериным с сотрудниками [33, 34]. Им создана лабораторная модель градиентного вихря небольшой интенсивности, но со значительным изменением тангенциальной скорости. С помощью вихреметра получена качественная Зависимость завихренности по радиусу со сменой знака вблизи границы ядра вихря.
Впоследствии тот же эффект был установлен Глейзером при обработке измерений, выполненных в природных вихрях типа торнадо [39]. Наличие смены знака завихренности свидетельствует о том, что природный вихрь имеет ядро, более стабилизированное от внешних возмущений, чем те вихри, которые описываются классическими уравнениями. Именно этим объясняется значительная продолжительность жизни смерчей с заданной концентрацией завихренности, не предсказываемая в рамках существующих теоретических представлений.
Факторы, которые отличают устойчивую градиентную вихревую трубку от закрученных потоков, могут быть связаны, согласно представлениям Кастерина — Предводителева, с величиной параметра β. Отношение продольных и поперечных размеров вихря в формуле, (6), по-видимому, определяет очень существенное для эффекта изменение знака завихренности соотношение размеров зоны осевой конвекции и зоны радиального притока к оси вихря и их месторасположение в пределах вихря. Соотношение μ/P0 в этой же формуле (6) характеризует зону перехода от вихревого движения к потенциальному. Причем, как показали наши наблюдения, это отношение существенно зависит от геометрии граничных поверхностей и в особенности тех, на которые задается вращение. Путем вариации тех факторов, которые пределяют изменение параметра, были реализованы условия смены знака завихренности.
Рис. 3. Завихренность на различных расстояниях
от центра вихревого столба воздуха; пунктир — расчет
на основе уравнений А. С. ПредводителеваНа рис. 3 представлена полученная нами кривая зависимости завихренности ω/ω0 , нормированной на ротор скорости, соответствующей границе вихря, от квадрата безразмерного расстояния до центра вихря. Обнаруженный в наших лабораторных исследованиях вихревых трубок [40, 41] эффект изменения знака завихренности, ранее наблюдавшийся только в природных вихрях и предсказанный Н. П. Кастериным, вызывает дополнительный интерес к тем методологическим приемам, которое использовались Н. П. Кастериным при изучении аэрогидродинамических явлений.
В плане развития предлагаемых Н. П. Кастериным представлений появляется возможность сформулировать новый подход к решению проблемы замыканий уравнений турбулентности для среднего молярного движения. Из гидродинамики хорошо известно, что векторное поле скоростей само себя не закручивает, т. е.
.
В случае турбулентного режима течения условие отсутствия закручиваемое имеет место как для поля среднего молярного движения
, которое описывается первым векторным уравнением Рейнольдса [14]
(7)
так и для поля скоростей v' относительного молярного движения (пульсационного), которое подчиняется второму векторному уравнению Рейнольдса [14]
(8)
Гипотеза замыкания уравнения (7) с нашей точки зрения может быть сведена к условию закручиваемости линий тока среднего молярного движения пульсационным, т. е.
.
Возьмем простейший вариант закручиваемости в виде условия параллельности векторов
, т.е.
(9)
Так как вектора
а также
попарно ортогональны, то как следствие условия (9) имеем:
, т.е.
(9')
Здесь τ — характерное время, c — некоторая функция времени, имеющая размерность скорости.
Возьмем операцию ротор от обеих частей уравнения Рейнольдса и подставим в полученные уравнения условия (9'). В линейном приближении получается система уравнений:
(10)
К полученным уравнениям мы присоединили условия несжимаемости вихревого потока. Связь векторов
в системе (10) напоминает поведение векторов
в электродинамике. Полученная система уравнений так же, как и максвелловская, содержит нестационарные решения в виде распространяющихся волн. Однако взаимосвязь полей среднего и пульсационного движений здесь имеет более сложный характер. В отсутствии турбулентности система (10) сводится к уравнениям Навье — Стокса.
ЛИТЕРАТУРА
1. Швейцер А. Культура и этика.— М.: Прогресс, 1972.
2. Кастерин Н. П. Обобщение основных уравнений аэродинамики и электродинамики.—М.: Изд-во АН СССР, 1937.
3. Helmholtz H. Die physikalische Bedentung des Prinzips der Kleinsten Wirkung.— «Wiss. Abh.», Bd 3.—Leipzig, 1895.
4. Helmholtz H. Vorlesungen tiber die Dynamik discreter Massenpunkte. Bd 1.— Leipzig, 1911.
5. Thomson В., Тait P. Treatise on natural philosophy. Part 1, 1879; Part 2, 1883. Cambridge.
6. Helmholtz H. Prinizipien der Statik monocyklisches Systeme.— «Wiss. Abh.», Bd 3.—Leipzig, 1895.
7. Герц Г. Принципы механики, изложенные в новой связи.— М.: Изд-во АН СССР, 1959.
8. Клейн Ф. Лекции о развитии математики в 19 столетии. Ч. 1.— М.: ОНТИ, 1937, с. 249—253.
9. Thomson J. J. Angewandungen der Dynamik auf Physik und Chemie. Leipzig, 1890.
10. Voss A. Die prinzipien der rationellen Mechanik.—In: Encyklopadie der Math. Wiss, Bd 4, Art. 1.—Leipzig, 1901.
11. Brill A. Vorlesungen zur Einfuhrung in die Mechanik raumerfullender Massen.— Leipzig, 1909.
12. Жуковский Н. Е. Полное собрание сочинений. Т. 9.—М.: ОНТИ, 1937, с. 260.
13. Дирак П. Эволюция физической картины мира.—В кн.: Элементарные частицы. Вып. 3.—М.: Наука, 1965.
14. Рейнольде О. Динамическая теория несжимаемой вязкой жидкости и опреде- ление критерия.— В кн.: Проблемы турбулентности. М., 1936.
15. Предводителев А. С. О молекулярно-кинетическом обосновании уравнений гидродинамики,—«Изв. АН СССР», 1948, № 4.
16. Predvoditelev A. S. On aerodynamics of rarefied gases and problems of heat transfer.—«Int. J. Heat. Mass Transfer», 1961, v. 3. p. 198.
17. Предводителев А. С. О дисперсии акустических волн в разреженных газах. — В кн.: Применение ультраакустики к исследованию вещества, вып. 8. М., 1959, с. 19—60.
18. Предводителев А. С. О вихревых движениях.— В кн.: Проблемы физической гидродинамики.—Минск, 1971, с. 178—212.
19. Предводителев А. С. О турбулентных течениях.—В кн.: Проблемы физиче- ской гидродинамики. — Минск, 1971, с. 212—236.
20. Предводителев А. С, Соловьев А. А. Новый взгляд на проблемы физиче- ской акустики.—М.: Изд-во МГУ, 1974.
21. Predvoditelev A. S., Bub now W. A. Pioneer paper N. P. Kasterin.—«Int. J. Heat. Mass Transfer», 1972, v. 15, p. 1185.
22. Лыков А. В. Тепломассообмен.— M.: Энергия, 1972.
23. Померанцев А. А. Физические начала тепломассообмена и газовой динамики.—М.: Энергия, 1977, с. 86—91.
24. Бубнов В. А. Молекулярно-кинетическое обобщение уравнений аэродинамики.— В кн.: Исследование термогидродинамических световодов.— Минск: ИТМО АН БССР, 1970, с. 100.
25. Lукоw A. W., Bubnow W. A. Uber mogliche verallgemeinertmgen der hydrody- namischen Gleichungen.— «ZAMM», 1973, Bd 53, S. 281.
26. Бубнов А. Об акустической дисперсии в разреженных газах.— «Инж. физ. журнал», 1976, т. 30, № 2, с. 295.
27. Грибкова С. И. Скольжение разреженного воздуха на поверхности движуще- гося тела.— «Вестн. Моск. ун-та, сер. физ., астр.», 1960, № 2, с. 21.
28. Грибкова С.И. Скольжение и коэффициент отражения молекул газа.— «Вестн. Моск. ун-та, сер. физ., астр.», 1960, № 3, с. 28.
29. Грибкова С. И. Изучение температурного скачка в разреженных газах.— «Вестн. Моск. ун-та, сер. физ., астр.», 1960, № 4, с. 59.
30. Бубнов В. А. Об эффекте Рейнера.— «Инж. физ. журнал», т. 30, № 1, с. 104.
31. Luikow A. V. Some Theological effects ingas mixtures.— Herceg Novi, 1970.
32. Шарц А. А. Экспериментальное исследование центростремительного эффекта Рейнера в жидкостях.—ПМТФ, 1977, т. 2, с. 105.
33 Кастерин Н. П. Устранение аэродинамического парадокса Феликса Клейна.— «Вестн. Моск. ун-та, сер. физ., астр.», 1948, № 10, с. 45—51.
34. Кастерин Н. П., Тимирязев А. К., Свиридов Т. М. Опытное получение воздушного вихревого столба.— «Вестн. Моск. ун-тa, сер. физ., астр.», 1949, № 10, с. 53—58.
35. Соловьев А. А., Хусаинова Б. Н. Аэродинамические уравнения свободного вихря.—В кн.: Солнечно-земные связи в метеорологии.— М.: Наука, 1980, с. 47—50.
36. Баранов П. А., Бубнов В. А., Соловьев А. А. Применение волоконных световодов в лазерных анемометрах.— В кн.: Методы' допплеровской диагностики в гидроаэродинамике.— Минск, 1978. с. 174.
37. Соловьев А. А., Хусаинова Б. Н. Динамические характеристики лабора- торных моделей торнадо. — В кн.: Солнечно-земные связи в метеорологии. — М.: Наука, 1980, с. 50—53.
38. Лыков А. В., Берковский Б. М. Конвекция и тепловые волны.- М.: Энергия, 1974, с. 244—249.
39. Глейзер А. Структура вихря торнадо по данным наблюдений. — В кн.: Дина- мика кучевых облаков.— М.: Мир, 1964.
40. Mapтыненко О. Г., Бубнов В. А., Соловьев А. А. Экспериментальные исследования вихревых трубрк. — В кн.: Процессы тепло- и массобмена в элементах термооптических устройств.—Минск: ИТМО АН БССР, 1979, с. 79—109.
41. Баранов П. А., Соловьев А. А. Измерения лазерным анемометром и зон- дом в лабораторных моделях торнадо.— «Изв. АН СССР, сер. физ. атм. и океана», 1980, № 5.