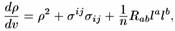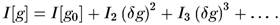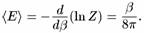Конец науки

Акимов О.Е.

4. Вершина спекулятивной науки

• Коротко о "Природе пространства и времени"
• Стивен Хокинг о квантовых черных дырах
• Роджер Пенроуз о квантовой теории и пространстве-времени
• Хокинг о квантовой космологии
• Пенроуз о квантовой космологии
• Хокинг о физической реальности
• Пенроуз о физической реальности
• Из книги "Природа пространства и времени"
• Предисловие (Майкл Атья)
• Классическая теория (Стивен Хокинг)
• Структура пространственно-временных сингулярностей (Роджер Пенроуз)
• Квантовые черные дыры (Стивен Хокинг)

В совместно прочитанных в 1994 году шести лекциях Стивена Хокинга и Роджера Пенроуза «Природе пространства и времени», спекулятивная наука, кажется, достигла пика. Когда наши потомки будут изучать природу научного кризиса периода XX — XXI веков, они, непременно, обратятся к этим лекциям, которые в сокращенном виде были опубликованы в журнале Scientific American за июль 1996 год и более полно представлены отдельной книгой.

Так вот для будущих историков науки хочу сообщить немаловажную информацию. Многие современные журналисты, философы и прочий любопытствующий люд принимают Хокинга и Пенроуза за серьезных ученых. На самом же деле их славят только за тем, чтобы в обществе не угас интерес к науке. Подобную мысль уже высказал Джон Хорган в своей книге «Конец науки». К этому я хочу лишь добавить следующее соображение.

Известно, что реальные исследования окружающего нас мира нуждаются в огромных деньгах. В связи с этим управленцам научной сферы крайне необходимо «раскручивать» поп-звезды, как это делается в шоу-бизнесе. Тогда дюжина странных «теоретиков» сможет привлечь в бюджет науки миллиарды долларов, которые покроют расходы на дорогостоящие космические аппараты и ускорители. Между тем наукообразные фантазии Хокинга и Пенроуза ровным счетом ничего не стоят — ни в прямом, ни в переносном смысле. Таким образом, народная наука снабжает профессиональную науку не какими-то оригинальными идеями, а в основном финансовыми средствами, которые истинные исследователи никогда бы сами не получили.

В связи с этим, я думаю, можно слегка потратиться и на поиск чёрных дыр и темной материи, притворяясь, будто эти экзотические объекты неуёмной фантазии народных ученых действительно существуют. Можно даже слегка приврать, говоря, будто открыто нечто, очень похожее на черную дыру и темную материю. Этот небольшой выброс сенсационной информации позволит заметно стимулировать интерес к науке, без которого всё пришло бы в кладбищенский упадок.

Такие процессы, по-видимому, протекают бесхитростно сами собой. Я думаю, что в среде профессионалов всегда найдется влиятельное лобби, которое ставит своей задачей подтвердить истинность народной науки. Люди, контролирующие большие денежные потоки, наверняка, связаны толстой пуповиной с народом. Пусть ученый совет из высококлассных специалистов решит потратиться на какую-то реальную программу исследований, все равно лобби народной науки отрежет для своих иллюзорных целей ломоть денежного пирога.

Указанный механизм саморегулирования сработал, например, в Пулковской обсерватории. До 1983 года ее возглавлял серьезный ученый М.С. Зверев, являющийся сторонником классической астрономии. Его сменил В.К. Абалакин, который навязал сотрудникам ЛО ВАГО несколько исследовательских программ, связанных с теорией относительности. При уточнении планетарных орбит он просил учесть релятивистские поправки, рассчитанные по методики В.А. Брумберга (см. книгу «Релятивистская небесная механика»). Между тем многие рядовые сотрудники обсерватории не верили не только в общую теорию относительности, на которую опирался Брумберг, но весьма скептически относились к специальной теории относительности, поскольку во всех расчетах, где требовалось складывать скорость небесного тела со скоростью свете (классический пример: спутники Юпитера), использовалась классическая формула сложения, а не релятивистская.

Ниже представлены фрагменты наиболее известной работы по спекулятивной «небесной механике», которая утвердилась в науке после прихода в нее Эйнштейна. Если релятивистская механика еще как-то было связана с эмпирическими данными и опиралась на элементы конструктивной математики, то механика Хокинга и Пенроуза полностью лишена этих «пережитков прошлого». Их физика целиком выведена из буйной фантазии авторов, которые для «онаучивания» своего сказочного повествования привлекли множество схематических чертежей. Разбросанные по тексту то там то сям математические выражения, как и рисунки, несут чисто иллюстративную нагрузку. Какая-либо связь между формулами, рисунками и реальностью, конечно, отсутствует.

Конструктивно думающий читатель потеряет время зря, если попытается проникнуть в смысл нижеприводимого текста. Его задача, как мне представляется, состоит лишь в усвоении некой спекулятивной формы подачи псевдонаучного материала. По лекциям Хокинга и Пенроуза «Природе пространства и времени» он может проследить нарастание формалистских элементов, сравнивая их с такими же спекулятивными элементами, присутствующими, например, в работах Эйнштейна и Бора. Еще он может поискать принципиальные различия в изложении материала, представленного в этих лекциях, и материала, образующего содержания конструктивных работ, например, Максвелла, Больцмана и Дж. Дж. Томсона.

Коротко о "Природе пространства и времени"

C. Хокинг, Р. Пенроуз
Scientific American, июль 1996
Перевод Андрея Крашеницы

В 1994 Стивен Хокинг и Роджер Пенроуз прочли цикл публичных лекций по общей теории относительности в Институте Математических Наук имени Исаака Ньютона при Кембриджском университете. Наш журнал представляет вам выдержки из этих лекций, выпущенных в этом году издательством Princeton University Press под названием "Природа пространства и времени", которые позволяют сравнить взгляды этих двух ученых. Хотя оба они и принадлежат к одной школе в физике (Пенроуз ассистировал докторскую диссертацию Хокинга в Кембридже), их взгляды на роль квантовой механики в эволюции вселенной сильно отличаются друг от друга. В частности Хокинг и Пенроуз имеют различные представления о том, что происходит с информацией, запасенной в черной дыре и почему начало вселенной отличается от ее конца.

Одно из главных открытий Хокинга, сделанных им в 1973, было предсказание того, что вследствие квантовых эффектов черные дыры могут испускать частицы. В результате такого процесса черная дыра испаряется, и в конечном счете возможно что от ее первоначальной массы ничего не останется. Но в течение своего формирования черные дыры поглощают множество падающих на нее частиц имеющих различные типы, свойства и конфигурации. Хотя квантовая теория требует, чтобы подобная информация была сохранена, подробности того, что же происходит с ней дальше, остаются темой для бурных дебатов. Хокинг и Пенроуз, оба полагают что, во время излучения черная дыра теряет информацию, которую она содержала в себе. Но Хокинг упорно утверждает, что эта потеря невосполнима, тогда как Пенроуз доказывает, что она сбалансирована спонтанными измерениями квантовых состояний, которые вводят информацию обратно внутрь черной дыры.

Оба ученых соглашаются с тем, что будущая теория квантовой гравитации необходима для описания природы. Но их взгляды отличаются на некоторые аспекты этой теории. Пенроуз считает, что даже если фундаментальные взаимодействия элементарных частиц симметричны по отношению к обращению времени, то квантовая гравитация должна нарушать такую симметрию. Временная асимметрия должна тогда объяснить, почему в начале вселенная была столь однородна (как показывает микроволновое фоновое излучение, рожденное большим взрывом), тогда как в конце вселенная должна быть неоднородна.

Пенроуз пытается включить подобную асимметрию в свою гипотезу Вейлевской кривизны. Пространство-время, согласно Альберту Эйнштейну, искривлено присутствием материи. Но пространство-время может также иметь некоторую внутренне присущую ему деформацию, обозначаемую как Вейлевская кривизна. Гравитационные волны и черные дыры, например, позволяют пространству-времени искривляться даже в тех областях, которые являются пустыми. В ранней вселенной Вейлевская кривизна была вероятно равна нулю, но в угасающей вселенной, как доказывает Пенроуз, большое количество черных дыр приведет к росту Вейлевской кривизны. В этом и будет заключаться различие между началом и концом вселенной.

Хокинг соглашается, что большой взрыв и заключительный коллапс ("Big crunch") будут различны, но он не рассматривает асимметрию времени в качестве закона природы. Основной же причиной для этого различия, как он думает, является тот путь, на который запрограммировано развитие вселенной. Он постулирует своего рода демократию, заявляя, что во вселенной не может быть выделенной пространственной точки; и поэтому, вселенная не может иметь границу. Именно это предложение об отсутствии границы, как утверждает Хокинг, объясняет однородность микроволнового фонового излучения.

Взгляды обоих физиков на интерпретацию квантовой механики также в корне расходятся. Хокинг полагает, что единственное предназначение теории — давать предсказания, которые согласуются с опытными данными. Пенроуз же считает, что простое сравнение предсказаний с экспериментами не достаточно для объяснения действительности. Он указывает, что квантовая теория, требующая суперпозиции волновых функций, есть концепция, которая может приводить к нелепости. Эти ученые таким образом возводят на новый виток известную дискуссию Эйнштейна и Бора по поводу причудливых последствий квантовой теории.

Стивен Хокинг о квантовых черных дырах

Квантовая теория черных дыр ..., кажется, приводит к новому уровню непредсказуемости в физике помимо обычной квантовомеханической неопределенности. Это происходит благодаря тому, что черные дыры, кажется, имеют внутреннюю энтропию и теряют информацию из нашей области вселенной. Я должен сказать, что эти требования весьма спорны: много ученых, работающих в области квантовой гравитации, включая почти всех тех, кто пришел в нее из физики элементарных частиц, инстинктивно отклоняют идею, что информация о состоянии квантовой системы может быть утеряна. Однако, такая точка зрения не привела к большому успеху в объяснении того, каким образом информация может покидать черную дыру. В конечном счете я полагаю, что они будут вынуждены принять мое предложение, что информация безвозвратно теряется, также, как они были вынуждены согласиться, что черные дыры излучают, что противоречит всем их предубеждениям ...

Тот факт, что гравитация является притягивающей, означает, что во вселенной имеет место тенденция стягивания материи в одном месте, тенденция к формированию объектов подобных звездам и галактикам. Дальнейшее сжатие этих объектов может некоторое время сдерживаться тепловым давлением, в случае звезд, или вращением и внутренними движениями, в случае галактик. Однако, в конечном счете теплота или угловой импульс будут унесены прочь, и объект опять начнет сжиматься. Если масса меньше чем, приблизительно полторы массы Солнца, сжатие может быть остановлено давлением вырожденного газа электронов или нейтронов. Объект стабилизируется, чтобы стать белым карликом или нейтронной звездой, соответственно. Однако, если масса больше чем этот предел, то уже нет ничего, что могло бы остановить неуклонное сжатие. Как только сжатие объекта приблизится к некоторому критическому размеру, поле тяготения на его поверхности будет настолько сильно, что световые конусы будут наклонены внутрь .... Мы можем видеть, что даже уходящие во вне световые лучи изогнуты по направлению друг к другу, так что они сближаются, а не расходятся. Это означает, что имеется некоторая закрытая поверхность ....

Таким образом должна существовать область пространства-времени, из которой невозможно вырваться на бесконечное расстояние. Эта область называется черной дырой. Ее граница называется горизонтом событий, она является поверхностью, сформированной световыми лучами, не способными вырваться к бесконечности ....

Большое количество информации теряется, когда космическое тело коллапсирует, чтобы образовать черную дыру. Коллапсирующий объект описывается очень большим количеством параметров. Его состояние определятся видами вещества и мультипольными моментами распределения их масс. Несмотря на это формирующаяся черная дыра совершенно не зависит от вида вещества и быстро теряет все мультипольные моменты кроме первых двух: монопольного, который является массой, и дипольного, который является моментом импульса.

Эта потеря информации действительно не имела значения в классической теории. Можно сказать, что вся информация относительно коллапсирующего объекта оказывается внутри черной дыры. Для наблюдателя, находящегося вне черной дыры, было бы очень трудно определить, на что похож коллапсирующий объект. Однако, в классической теории это было все еще возможно в принципе. Наблюдатель никогда фактически не терял бы из виду коллапсирующий объект. Вместо этого, ему казалось бы, что объект замедляется в своем сжатии и становится все более и более тусклым, по мере его приближения к горизонту событий. Этот наблюдатель все еще мог видеть из чего состоит коллапсирующий объект и как в нем распределена масса.

Однако, с точки зрения квантовой теории все полностью меняется. В течение коллапса объект испустил бы только ограниченное число фотонов прежде, чем пересечь горизонт событий. Этих фотонов было бы соверщенно недостаточно, чтобы передать нам всю информацию относительно коллапсирующего объекта. Это означает, что в квантовой теории не существует никакого способа, которым внешний наблюдатель мог бы определить состояние такого объекта. Можно было бы подумать, что это не имеет слишком большого значения, потому что информация будет все еще внутри черной дыры, даже если ее невозможно измерить извне. Но это как раз тот случай, где проявляется второй эффект квантовой теории черных дыр....

Квантовая теория заставляет черные дыры излучать и терять массу. И по-видимому они в конечном счете исчезают полностью — вместе с информацией внутри них. Я хочу привести аргументы в пользу того, что эта информация действительно теряется и не возвращается в какой-либо форме. Как я покажу дальше, с этой потерей информации в физику входит неопределенность более высокого уровня чем обычная неопределенность, связанная с квантовой теорией. К сожалению, в отличие от соотношения неопределенности Гейзенберга, этот новый уровень неопределенности будет довольно трудно подтвердить экспериментально в случае черных дыр.

Роджер Пенроуз о квантовой теории и пространстве-времени

Квантовая теория, специальная теория относительности, общая теория относительности и квантовая теория поля — величайшие физические теории 20-ого столетия. Эти теории не независимы от друг друга: общая теория относительности была построена на основе специальной теории относительности, а квантовая теория поля имеет специальную теорию относительности и квантовую теорию в качестве своего основания.

Обычно говорилось, что квантовая теория поля — наиболее точная из всех когда-либо существовавших физических теорий, дающая точность до 11 знаков после запятой. Однако, я хотел бы указать, что общая теория относительности в настоящее время проверена с точностью до 14 знаков после запятой (и эта точность очевидно ограничена только точностью часов, идущих на Земле). Я имею в виду бинарный пульсар Hulse-Taylor PSR 1913+16, пара нейтронных звезд вращающихся друг относительно друга, одна из которых — пульсар. Общая теория относительности предсказывает, что подобная орбита медленно сжимается (а ее период уменьшается), потому что происходит потеря энергия вследствие излучения гравитационных волн. Этот процесс действительно был зафиксирован экспериментально, а полное описание его движения, наблюдаемого в течение 20 лет ... находится в согласии с общей теорией относительности (которая включает в себя Ньютоновскую теорию) с замечательной точностью, отмеченной выше. Исследователи этой звездной системы по праву получили Нобелевские премии за свою работу. Квантовые теоретики всегда утверждали, ссылаясь на точность их теории, что общая теория относительности должна брать с нее пример, но я думаю теперь, что пример должна брать квантовая теория поля.

Хотя эти четыре теории достигли больших успехов, но и они не свободны от проблем .... Общая теория относительности предсказывает существование сингулярностей пространства-времени. В квантовой теории имеется "проблема измерения", я опишу ее позже. Может оказаться, что решение проблем этих теорий состоит в признании того факта, что они являются неполными теориями. Например, многие предвкушают, что квантовая теория поля могла бы каким-либо способом "размазать" сингулярности общей теории относительности....

А теперь я хотел бы сказать несколько слов относительно потери информации в черных дырах, которая, как я полагаю, имеет отношение к последнему утверждению. Я соглашаюсь почти со всем, что относительно этого сказал Стивен. Но в то время как Стивен расценивает потерю информации в черных дырах как новую неопределенность в физике, более высокого уровня, чем квантовомеханическая неопределенность, то я же рассматриваю ее как всего лишь "дополнительную" неопределенность .... Возможно, что небольшое количество информации теряется во время испарения черной дыры ... но этот эффект будет намного меньше, чем потеря информации во время коллапса (для описания которого я принимаю любую разумную картину заключительного исчезновения черной дыры).

В качестве мысленного эксперимента рассмотрим замкнутую систему в большом ящике и рассмотрим движение материи внутри ящика в фазовом пространстве. В областях фазового пространства, соответствующих местоположениям черной дыры, траектории описывающие физическую эволюцию системы будут сходиться, и фазовые объемы, заполняемые этими траекториями, будут сокращаться. Это происходит в результате потери информации в сингулярности черной дыры. Данное сокращение находится в прямом противоречии с законом классической механики, известным как теорема Лиувилля, которая утверждает, что фазовые объемы, переносимые фазовыми траекториями остаются постоянными .... Таким образом пространство-время черной дыры нарушает сохранение таких объемов. Однако, в моей картине, эта потеря объема фазового пространства сбалансирована процессом спонтанных квантовых измерений, в результате которых происходит восстановление информации и увеличение объема в фазовом пространства. Как понимаю это я, так происходит потому, что неопределенность, связанная с потерей информации в черных дырах, является как бы "дополнительной" к квантовомеханической неопределенности: каждая из них — лишь одна сторона одной монеты....

А теперь давайте рассмотрим мысленный эксперимент с котом Шредингера. Он описывает незавидное положение кота в ящике, в котором испущенный фотон падает на полупрозрачное зеркало, а переданная часть его волновой функции регистрируется датчиком. Если датчик обнаруживает фотон, то срабатывает пистолет, убивающий кота. Если датчик не обнаруживает фотон, то кот остается жив и здоров. (Я знаю, что Стивен не одобряет дурное обращение с котами, даже в мысленных экспериментах!) Волновая функция такой системы является суперпозицией этих двух возможностей .... Но почему нашему восприятию доступны только макроскопические альтернативы "кот мертв" и "кот жив", а не макроскопические суперпозиции таких состояний? ...

Я предполагаю, что с привлечением общей теории относительности, использование суперпозиций альтернативных геометрий пространства-времени сталкивается с серьезными трудностями. Возможно, что суперпозиция двух различных геометрий нестабильна и распадается в одну из этих двух альтернатив. Такими геометриями могли бы быть, например, пространство и время живого или мертвого кота. Для обозначения этого распада суперпозиции в одно из альтернативных состояний я использую термин объективная редукция, который мне нравится, потому что имеет хороший акроним (OR). Какое отношение к этому имеет планковская длина 10-33 сантиметра? Такая длина является естественным критерием для определения того, являются ли геометрии действительно различными мирами. Планковский масштаб определяет также и временной масштаб, при котором происходит редукция в различные альтернативы.

Хокинг о квантовой космологии

Я заканчиваю эту лекцию обсуждением вопроса, по поводу которого Роджер и я имеем различные взгляды — это стрела времени. Имеется очень ясное различие между прямым и обратным направлениями времени в нашей части вселенной. Достаточно прокрутить назад любой фильм, чтобы увидеть это различие. Вместо чашек, падающих со стола и рассыпающихся на мелкие кусочки, мы видели бы как эти осколки вновь собираются вместе и вскакивают обратно на стол. Разве реальная жизнь похожа не что-либо подобное?

Локальные законы физические полей удовлетворяют требованию симметрии во времени, или если быть более точным CPT-инвариантности (Charge-Parity-Time — Заряд-Четность-Время). Таким образом, наблюдаемое различие между прошлым и будущим происходит от граничных условий вселенной. Рассмотрим модель, в которой пространственно замкнутая вселенная расширяется до максимального размера, после чего вновь коллапсирует. Как подчеркнул Роджер, вселенная будет сильно различается в конечных пунктах этой истории. В своем начале вселенная, как мы теперь думаем, будет довольно гладкой и регулярной. Однако, когда она начнет снова коллапсировать, мы ожидаем, что она будет чрезвычайно беспорядочна и нерегулярна. Поскольку беспорядочных конфигураций гораздо больше чем упорядоченных, это означает, что начальные условия должны быть выбраны чрезвычайно точно.

Вследствие этого граничные условия должны быть различными в эти моменты времени. Предположение Роджера состоит в том, что Вейлевский тензор должен обратиться в нуль только в одном из концов времени. Вейлевский тензор — та часть кривизны пространства-времени, которая не определяется локальным распределением материи через уравнения Эйнштейна. Эта кривизна чрезвычайно мала в упорядоченной ранней стадии, и очень велика в коллапсирующей вселенной. Таким образом, это предложение позволило бы нам отличить оба конца времени друг от друга и объяснить существование стрелы времени.

Я думаю, что предложение Роджера является Вейлевским в двух смыслах этого слова. Во-первых, оно — не CPT-инвариантно. Роджер рассматривает это свойство как достоинство, но как я чувствую, не нужно отказываться от симметрий без достаточно весомых на то причин. Во вторых, если бы Вейлевский тензор был точно равен нулю на ранней стадии вселенной, то она оставалась бы однородной и изотропной в течение всего последующего времени. Вейлевская гипотеза Роджера не может объяснять ни флуктуации микроволнового фона, ни возмущения, которые вызывают галактики и тела, подобные нам самим.

Несмотря на все это, я думаю, что Роджер указал на очень важное различие между этими двумя границами времени. Но факт, что малость Вейлевского тензора в одной из границ, не должна приниматься нами ad hoc, а должна быть получена из более фундаментального принципа "отсутствия границ" ....

Каким образом две временные границы могут быть различными? Почему возмущения должны быть малы в одной из них, но не в другой? Причина этого в том, что уравнения поля имеют два возможных комплексных решения.... Очевидно, что одно решение соответствует одной границе времени, а другое — другой .... В одном конце времени, вселенная была очень гладкой, и Вейлевский тензор — мал. Однако, точно он не мог быть равен нулю, поскольку это приводит к нарушению соотношения неопределенности. Вместо этого должны иметь место небольшие флуктуации, которые позже могут превратиться в галактики и тела, подобно нам самим. В противоположность началу, конец вселенная должен быть очень нерегулярным и хаотичным, а Вейлевский тензор очень большим. Это объяснило бы почему имеет место стрела времени и почему чашки падают со стола и разбиваются гораздо охотнее, чем восстанавливаются и вскакивают обратно.

Пенроуз о квантовой космологии

Из того, что я понял в концепции Стивена, я делаю вывод, что наши разногласия по данному вопросу (Вейлевская гипотеза кривизны) чрезвычайно велики ...Для начальной сингулярности Вейлевская кривизна приблизительно является нулевой .... Стивен спорил, что в начальном состоянии должны иметь место маленькие квантовые флуктуации, и поэтому гипотеза о нулевой Вейлевской кривизне является классической и неприемлемой. Но я думаю, что имеется некоторая свобода относительно точной формулировки этой гипотезы. Маленькие возмущения конечно же приемлемы с моей точки зрения в квантовом режиме. Мы нуждаемся только в том, чтобы существенно ограничить эти флуктуации около нуля ....

Возможно, что принцип "отсутствия границ" Джеймса-Хартли-Хокинга является хорошим кандидатом для описания структуры начального состояния. Однако, как мне кажется, для объяснения заключительного состояния необходимо что-то другое. В частности, теория, объясняющая структуру сингулярностей, должна была бы включать в себя нарушение CPT и других симметрий, для того чтобы быть совместимой с гипотезой Вейлевской кривизны. Такое нарушение симметрии времени могло бы быть весьма малым; и могло бы неявно содержаться в новой теории, выходящей за пределы квантовой механики.

Хокинг о физической реальности

Эти лекции очень ясно показали различие между Роджером и мной. Он — платонист, а я — позитивист. Он всерьез озабочен, что кот Шредингера находится в квантовом состоянии, в котором он наполовину жив, а наполовину мертв. Он предчувствует в этом несоответствие действительности. Но меня такие вещи не беспокоят. Я не требую, чтобы теория соответствовала реальности, поскольку не знаю, что такое реальность. Реальность это не качество, которое вы можете проверить лакмусовой бумагой. Все, о чем я беспокоюсь это то, чтобы теория предсказывала результаты измерений. Квантовая теория делает это очень успешно ....

Роджер чувствует, что ... коллапс волновой функции привносит в физику нарушение CPT-симметрии. Он видит такие нарушения в работе по крайней мере в двух областях физики: космология и черные дыры. Я соглашаюсь, что мы можем использовать асимметрию времени, когда задаем вопросы относительно наблюдений. Но я полностью отклоняю идею, что имеются некие физические процессы, приводящие к редукции волновой функции, или что это имеет какое-либо отношение к квантовой гравитации или сознанию. Это все имеет отношение к волшебству и магии, но не к науке.

Пенроуз о физической реальности

Квантовая механика существует всего только 75 лет. Это не очень много, особенно если сравнивать, например, с теорией гравитации Ньютона. Поэтому я не удивлюсь, если квантовая механика будет модифицирована для очень больших объектов.

В начале этих дебатов Стивен высказал мысль, что он—- позитивист, а я — платонист. Я рад, что он позитивист, но относительно себя могу сказать, что я скорее являюсь реалистом. К тому же, если сравниваете эти дебаты с известными дебатами Бора и Эйнштейна, приблизительно 70 лет назад, я думаю, что Стивен играет роль Бора, а я — роль Эйнштейна! Для Эйнштейна было необходимо, чтобы существовало нечто похожее на реальный мир, описываемое не обязательно волновой функцией, в то время как Бор подчеркивал, что волновая функция не описывает не реальный мир, а только знание, необходимое для предсказания результатов эксперимента.

Сейчас считается, что аргументы Бора оказались более весомыми, и что Эйнштейн (согласно его биографии, написанной Абрахамом Паисом) мог уже с 1925 года заниматься рыбалкой. И действительно, он не внес большого вклада в квантовую механику, хотя его проницательная критика была очень полезна для последней. Я полагаю, что причина этого была в том, что в квантовой теории отсутствовали некоторые важные компоненты. Одним из таких компонентов было открытое Стивеном 50 годами позже излучения черных дыр. Утечка информации, связанная с излучением черной дыры, есть тот феномен, который возможно поднимет квантовую теорию на новый уровень.

Из книги "Природа пространства и времени"

С. Хокинг, Р. Пенроуз

(Взято с сайта http://yanko.lib.ru)

Перевод с английского А. В. Беркова, В. Г. Лебедева
Научно-издательский центр «Регулярная и хаотическая динамика»
Удмуртский государственный университет – 2000.

УДК 530.1
Хокинг С, Пенроуз Р. Природа пространства и времени. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000, 160 стр.
Основное содержание книги состоит из шести лекций, предваряющих дискуссию, и изложение самой дискуссии, прошедшей между Хокингом и Пенроузом по некоторым наиболее фундаментальным вопросам, связанным с природой Вселенной. К этим вопросам можно отнести «стрелу времени», начальные условия рождения Вселенной, поглощение информации черными дырами и др. Дискуссия в значительной мере является продолжением сольвеевского спора Бора и Эйнштейна по основам квантовой механики.
Для широкой аудитории читателей, интересующихся проблемами современной физики и космологии.
ISBN 5-93972-003-Х
All right reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording or by any information storage and retrieval system, without permission in writing from the Publisher.
© Удмуртский государственный университет, НИЦ «Регулярная и хаотическая динамика», 2000
http://www.гcd.com.ru

Предисловие

Дискуссия между Роджером Пенроузом и Стивеном Хокингом, представленная в этой книге, явилась вершиной шестимесячной программы, проведенной в 1994 году в Институте математических наук имени Исаака Ньютона при Кембриджском университете. Дискуссия посвящена серьезному обсуждению некоторых наиболее фундаментальных идей, касающихся природы Вселенной. Излишне говорить, что мы пока еще далеки от конца пути. До сих пор существует множество неясных и спорных моментов и вопросов для обсуждения.

Около 60 лет назад произошел знаменитый продолжительный спор между Нильсом Бором и Альбертом Эйнштейном по основам квантовой механики. Эйнштейн отказался принять точку зрения, согласно которой квантовая механика является окончательной теорией. Считая ее философски неадекватной, он начал упорную борьбу против ортодоксальной интерпретации копенгагенской школы, которой придерживался Бор.

В определенном смысле дискуссия между Пенроузом и Хокингом является продолжением этого давнего спора, с той разницей, что роль Эйнштейна играет Пенроуз, а роль Бора — Хокинг. Обсуждаемые вопросы стали сложнее и разнообразнее, но, как и раньше, они представляют комбинацию технических рассуждений и философских точек зрения.

Квантовая теория или ее более утонченная версия — квантовая теория поля в настоящий момент является наиболее продвинутой и технически очень успешной, несмотря на то, что существуют такие философски настроенные скептики, как Роджер Пенроуз. Общая теория относительности, т.е. эйнштейновская теория гравитации, также выдержала проверку временем и может претендовать на замечательный успех, хотя в ней до сих пор существуют серьезные проблемы, касающиеся роли сингулярностей и черных дыр.

В дискуссии Хокинга и Пенроуза доминирует обсуждение вопроса о том, как построить теорию «квантовой гравитации», комбинируя эти две успешные теории. «Квантовая гравитация» имеет глубокие концептуальные и технические проблемы, которые обеспечивают необходимый простор для аргументов, приводимых в этих лекциях.

Обсуждаемые фундаментальные вопросы включают в себя «стрелу времени», начальные условия при рождении Вселенной и механизм поглощения информации черными дырами. По всем этим, а так же многим другим вопросам позиции Хокинга и Пенроуза несколько различаются. Их доводы как математически, так и физически корректны, а форма обсуждения позволяет разумным образом обмениваться критическими замечаниями.

Хотя некоторые из обсуждаемых вопросов требуют понимания математики и физики на технически продвинутом уровне, большая часть рассуждений проводится на более высоком (или более глубоком) уровне, представляющем интерес для широкой аудитории. По крайней мере, читатель получит представление о масштабности и тонкости идей, обсуждаемых в книге, а также о громадном вызове, который стоит перед современной наукой в достижении согласованной картины Вселенной, полностью учитывающей как законы гравитации, так и квантовую теорию.

Майкл Атья

Классическая теория

Стивен Хокинг

В этих лекциях Роджер Пенроуз и я хотели изложить наши связанные друг с другом и в то же время различные точки зрения на природу пространства и времени. Каждый из нас по очереди прочтет по три лекции, после чего последует обсуждение наших различных подходов. Я должен подчеркнуть, что это будут достаточно технические лекции. Так, мы подразумеваем, что читателю известны основные понятия общей теории относительности и квантовой теории.

Существует короткая статья Ричарда Фейнмана, излагающая его понимание ситуации на конференции по общей теории относительности. По-моему, это была Варшавская конференция 1962 года. В ней были высказаны нелицеприятные замечания по поводу общей компетентности участников конференции и уместности того, чем они занимаются. В том, что общая теория относительности вскоре приобретет гораздо лучшую репутацию и вызовет больший интерес, мы во многом обязаны работам Роджера Пенроуза.

До этих работ общая теория относительности формулировалась в виде беспорядочного набора уравнений в частных производных в единственной координатной системе. Люди настолько радовались, когда находили решение этих уравнений, что не заботились о том, что эти решения, возможно, не имеют физического смысла. Однако Роджер внес в эту область такие современные концепции, как спиноры и глобальные методы качественного анализа. Он первый показал, как можно изучать общие свойства уравнений теории относительности без точного их решения. Именно ему принадлежит первая теорема о сингулярностях, которая привела меня к изучению причинной структуры и инспирировала мою классическую работу по сингулярностям и черным дырам.

Я думаю, Роджер и я в значительной мере согласны друг с другом, когда речь идет о явлениях в классической области. Однако мы отличаемся в наших подходах к квантовой гравитации и, на самом деле, к самой квантовой теории. Хотя физики, занимающиеся частицами, считают меня опасным радикалом за предложение о возможной потере квантовой когерентности, я определенно консерватор по сравнению с Роджером. Я принимаю позитивистскую точку зрения, что физическая теория есть просто математическая модель, и что бессмысленно спрашивать, соответствует ли ей какая-либо реальность. Вместо этого мы можем лишь спросить, находятся ли ее предсказания в согласии с соответствующими наблюдениями. Мне кажется, что Роджер в сердце платонист, но ответ на этот вопрос он должен дать самому себе.

Хотя и предлагались гипотезы о том, что пространство-время может иметь дискретную структуру, я не вижу причин отвергать непрерывные теории, которые оказались столь успешными. Общая теория относительности является прекрасной теорией, которая согласуется со всеми выполненными наблюдениями. Возможно она потребует модификации на планковских масштабах, но я не думаю, что это повлияет на большинство предсказаний, которые могут быть получены. Вполне возможно также, что общая теория относительности является лишь низкоэнергетическим приближением для некоторой более фундаментальной теории, подобной теории струн, которую, как мне кажется, сильно переоценили. Во-первых, до конца не ясно, почему общая теория относительности при комбинировании с другими полями в рамках теории супергравитации не может привести к разумной квантовой теории. Слухи о смерти супергравитации сильно преувеличены. То каждый верит, что супергравитация является окончательной теорией. Но уже на следующий год мода меняется, и каждый говорит, что супергравитация обречена на существование в ней расходимостей, хотя при этом никто их не обнаружил. Вторая причина, по которой я не хочу обсуждать теорию струн, состоит в том, что в ней не сделано проверяемых предсказаний. В противоположность этому, непосредственное применение квантовой теории к общей теории относительности, которую я буду обсуждать, уже имеет два проверяемых предсказания. Одно их них — развитие малых возмущений при инфляции — кажется, подтверждается недавними наблюдениями флуктуаций в микроволновом фоне. Другое предсказание о том, что черные дыры должны испускать равновесное тепловое излучение, в принципе проверяемо. Все, что необходимо — это найти первичную черную дыру. К сожалению, похоже, что в нашем рукаве Галактики их не так уж много. Если бы они были, мы бы сейчас уже знали, как квантовать гравитацию.

Ни одно из этих предсказаний не изменится, даже если окончательной теорией природы является теория струн. К сожалению, теория струн, по крайней мере на нынешнем уровне ее развития, не способна делать такие предсказания, не апеллируя к общей теории относительности как низкоэнергетической эффективной теории. Я подозреваю, однако, что это всегда будет так, и что не существует каких-либо наблюдаемых предсказаний в теории струн, которые не могут быть получены с помощью общей теории относительности или супергравитации. Если это так, то возникает вопрос, является ли теория струн действительно научной теорией. Является ли математическая красота и полнота достаточными критериями при отсутствии четко проверяемых наблюдаемых предсказаний? При этом следует учитывать, что в настоящий момент теория струн не является ни красивой, ни полной.

По этим причинам я буду говорить в этих лекциях только об общей теории относительности. Я сосредоточу внимание на двух областях, в которых гравитация, по-видимому, обладает свойствами, полностью отличающимися от других полевых теорий. Первой является идея о том, что благодаря гравитации пространство-время должно иметь начало, а возможно и конец. Второе — это открытие того, что, по-видимому, существует внутренняя гравитационная энтропия, не являющаяся результатом крупнозернистой структуры. Некоторые утверждают, что эти предсказания являются только артефактами полуклассического приближения. Они говорят, что струнная теория, истинная квантовая теория гравитации, размажет сингулярности и приведет к корреляциям в излучении черных дыр, так что оно только приближенно является тепловым, в крупнозернистом приближении. Если это так, то это будет довольно скучно. Гравитация будет тогда подобна любому другому полю. Но я убежден, что она существенно отлична от них, потому что гравитация формирует арену, на которой сама действует, в противоположность другим полям, которые действуют в заданном пространстве-времени. Именно это дает возможность времени иметь свое начало. Это также приводит к существованию ненаблюдаемых областей Вселенной, что в свою очередь приводит к понятию гравитационной энтропии как меры того, что мы можем не знать.

Рис. 1.1. Хронологическое будущее для точки p

В этой лекции я дам обзор работ в классической общей теории относительности, которые привели к этим идеям. В моих второй и третьей лекциях (главы 3 и 5) я покажу, как эти идеи изменяются и расширяются при переходе к квантовой теории. Моя вторая лекция будет посвящена черным дырам, а третья — квантовой космологии. Решающая для исследования сингулярностей и черных дыр техника, которая была введена Роджером, и которую я помогал развивать, состоит в изучении глобальной причинной структуры пространства-времени. Определим I⁺(р) как множество всех точек пространства-времени М, которые могут быть достигнуты из точки p времениподобными кривыми, направленными в будущее (рис. 1.1). Можно считать, что 1⁺(р) — это множество всех событий, на которые может влиять то, что происходит в точке р. Точно такое же определение можно ввести, заменив плюс на минус и будущее на прошлое. Я буду считать такие определения самоочевидными.

Можно рассмотреть границу I⁺(S) будущего для множества S. Нетрудно видеть, что эта граница не может быть времениподобной. Действительно, в этом случае точка q, находящаяся вне границы, была бы в будущем точки р, находящейся внутри границы. Граница будущего не может быть также пространственноподобной, исключая множество S само по себе. В этом случае каждая кривая из точки q, лежащая в будущем для границы и направленная в прошлое, будет пересекать границу и покидать будущее для S. Это противоречит тому факту, что q находится в будущем для S (см. рис. 1.2).

Рис. 1.2. Границы хронологического будущего не могут быть времениподобными или пространственноподобными

Рис. 1.3. Вверху: точка q лежит на границе будущего, так что существует нулевой геодезический сегмент на границе, который проходит через q.

Следовательно, можно заключить, что граница будущего является нулевой, в отличие от самого множества S. Более точно, если q принадлежит границе будущего, но не замыканию S, существует нулевой геодезический сегмент, направленный в прошлое и лежащий вместе с q на границе (рис. 1.3). Может существовать и более чем один нулевой геодезический сегмент, включающий q и лежащий на границе, но в этом случае q должна быть конечной точкой сегментов в будущем. Иными словами, граница будущего для S порождается нулевыми геодезическими, которые имеют на границе конечную точку в будущем и проходят во внутреннюю область будущего, если они пересекают другую нулевую геодезическую. С другой стороны, нулевые геодезические генераторы могут иметь конечные точки в прошлом только на S. Однако возможно рассматривать пространство-время, в котором существуют генераторы границы будущего множества S, которые никогда не пересекают S. Такие генераторы могут не иметь конечных точек в прошлом.

Рис. 1.4. При удалении линии из пространства Минковского, граница будущего для множества 5 будет иметь генератор, у которого нет конечных точек в прошлом

Простым примером является пространство Минковского с удаленным куском горизонтальной линии (рис. 1.4). Если множество S лежит в прошлом для горизонтальной линии, линия будет отбрасывать тень, в которой будут находиться точки, являющиеся будущими по отношению к этой линии и отсутствующие в будущем для S. Там должны быть генераторы границы будущего S, которые возвращаются к концу горизонтальной линии. Однако, поскольку конечная точка горизонтальной линии удалена из пространства-времени, генератор границы не может иметь конечных точек в прошлом. Такое пространство-время является неполным, однако это может быть исправлено умножением метрики на подходящий конформный множитель вблизи конца горизонтальной линии. Хотя такие пространства выглядят очень искусственно, они важны для демонстрации того, насколько следует быть аккуратным при изучении причинной структуры. Фактически, Роджер Пенроуз, который был одним из моих оппонентов при защите диссертации, указал, что пространство, которое я здесь описал, является контрпримером к сделанным в моей диссертации утверждениям.

Чтобы показать, что каждый генератор границы будущего имеет в своем множестве конечную точку в прошлом, следует потребовать выполнения некоторого глобального условия на причинную структуру. Наиболее сильное и физически наиболее важное условие состоит в требовании глобальной гиперболичности. Говорят, что открытое множество U является глобально гиперболическим, если:

1. для любой пары точек p и q в U пересечение будущего для p и прошлого для q имеет компактное замыкание. Другими словами, оно ограничено ромбовидной областью (рис. 1.5);

2. на U строго выполняется причинность. Это означает, что не существует замкнутых или почти замкнутых времениподобных кривых, содержащихся в U.

Рис. 1.5. Пересечение прошлого для q и будущего для p имеет компактное замыкание

Рис. 1.6. Семейство поверхностей Коши для U

Физическое значение глобальной гиперболичности следует из того факта, что она приводит к существованию семейства поверхностей Коши Ι(t) для U (рис. 1.6). Поверхность Коши для U является пространственноподобной или нулевой поверхностью, которая пересекает каждую времениподобную кривую в U один и только один раз. Можно предсказать, что произойдет в U, исходя из данных на поверхности Коши, а также сформулировать квантовую теорию поля с хорошим поведением на глобально гиперболическом фоне. Менее ясно, можно ли сформулировать разумную квантовую теорию поля на неглобальном гиперболическом фоне. Таким образом, глобальная гиперболичность может быть физически необходимой. Однако моя точка зрения состоит в том, что ее не надо предполагать, потому что глобальная гиперболичность может исключить что-то такое, о чем пытается нам сказать гравитация. Скорее, мы должны вывести, что определенные области пространства-времени являются глобально гиперболическими, исходя из каких-то других физически приемлемых предположений.

Рис. 1.7. В глобально гиперболическом пространстве существует геодезическая максимальной длины, соединяющая любую пару точек, которые могут быть соединены времениподобной или нулевой кривой

Важность глобальной гиперболичности для теорем об сингулярностях видна из последующего. Пусть U глобально гиперболично, и пусть p и q — точки U, которые могут быть соединены времениподобной или нулевой кривой. Тогда существует времениподобная или нулевая геодезическая между p и q, которая максимизирует длину времениподобных или нулевых кривых из p в q (рис. 1.7). Метод доказательства состоит в том, чтобы показать, что пространство всех времениподобных или нулевых кривых из p в q является компактным в определенной топологии. После этого можно показать, что длина кривой является верхней полунепрерывной функцией на этом пространстве. Следовательно, она должна достигать своего максимума, а кривая максимальной длины будет являться геодезической, поскольку в противоположном случае малое изменение будет приводить к более длинной кривой.

Рис. 1.8. Слева: если на геодезической существует сопряженная точка r между p и q, она не является геодезической минимальной длины. Справа: неминимальная геодезическая из p в q имеет сопряженную точку на южном полюсе

После этого можно рассмотреть вторую вариацию длины геодезической γ. Можно показать, что γ можно заменить на более длинную кривую, если существует бесконечно близкая геодезическая, идущая из р, которая снова пересекает γ в точке γ между p и q. Говорят, что точка r является сопряженной к p (рис. 1.8). Это можно продемонстрировать, рассматривая две точки p и q на поверхности Земли. Без потери общности можно взять точку p на северном полюсе.

Поскольку Земля имеет не лоренцевскую, а положительно определенную метрику, на ней существуют геодезические не максимальной, а минимальной длины. Минимальная геодезическая является линией долготы, проходящей через северный полюс к точке q. Но существует и другая геодезическая, из p в q, которая идет от северного полюса по другой стороне, проходит через южный полюс и попадает в q. Эта геодезическая содержит точку, сопряженную p на южном полюсе, где пересекаются все геодезические из р. Обе геодезические являются экстремумами длины при малых вращениях. Но теперь, при положительно определенной метрике, вторая вариация геодезической, содержащей сопряженную точку, может привести к более короткой кривой из p в д. Так, в примере с Землей можно получить, что геодезическая, которая идет вниз через южный полюс, а затем идет вверх, не является кратчайшей кривой из p в q. Этот пример довольно очевиден. Однако в случае пространства-времени можно показать, что при определенных предположениях должна существовать глобально гиперболическая область, в которой на каждой геодезической между двумя заданными точками существуют сопряженные точки. Это приводит к противоречию, показывающему, что предположение о полноте геодезических, которое было использовано как определение сингулярного пространства-времени, является ошибочным.

Причина возникновения сопряженных точек в пространстве-времени состоит в том, что гравитация является притягивающей силой. Следовательно, пространство-время искривляется таким образом, что соседние геодезические не удаляются друг от друга, а сближаются. Это можно увидеть из уравнений Раучадхури или Ньюмена-Пенроуза, которые я приведу в единой форме:

где n = 2 для нулевых геодезических, n = 3 для времениподобных геодезических.

Здесь v является аффинным параметром вдоль конгруэнций геодезических с касательным вектором l^a, который ортогонален к гиперповерхности. Величина ρ вявляется средней скоростью сближения геодезических, в то время как ρ измеряет напряжение. Слагаемое R_ab l^al^b определяет непосредственное гравитационное воздействие материи на сходимость геодезических.

Уравнение Эйнштейна

Слабое энергетическое условие

для любого времениподобного вектора va.

Из уравнений Эйнштейна следует, что последнее слагаемое будет неотрицательным для любого нулевого вектора l^a, если материя удовлетворяет так называемому слабому энергетическому условию. Оно утверждает, что плотность энергии T₀₀ является неотрицательной в любом базисе. Слабому энергетическому условию удовлетворяет классический тензор энергии-импульса любого разумного вида материи, такого как скалярное или электромагнитное поле или жидкость с приемлемым уравнением состояния. Однако это условие может локально не выполняться для квантово-механического среднего значения тензора энергии-импульса. Это будет существенно в моих второй и третьей лекциях (главы 3, 5).

Предположим, что слабое энергетическое условие справедливо, и что нулевые геодезические из точки p начинают снова сходиться, причем ρ имеет положительное значение ρ₀· Тогда из уравнений Ньюмена-Пенроуза следует, что сближение ρ может стать бесконечным в точке q внутри промежутка аффинного параметра размером , если нулевая геодезическая может быть так далеко продолжена.

Бесконечно близкие нулевые геодезические из p будут пересекаться в q. Это означает, что точка q будет сопряжена с p вдоль соединяющей их нулевой геодезической γ. Для точек на γ кроме точки q будет существовать такая вариация γ, которая дает времениподобную кривую из р. Такая геодезическая γ не может лежать на границе будущего точки p за сопряженной точкой q. Таким образом, γ будет иметь конечную точку в будущем как генератор границы будущего точки p (см. рис. 1.9).

Рис. 1.9. Точка q является сопряженной к р вдоль нулевых геодезических, так что нулевая Геодезическая γ, которая соединяет р с q, будет покидать границу будущего точки р в точке q.

Сильное энергетическое условие

Ситуация с времениподобными геодезическими аналогична, за исключением того, что сильное энергетическое условие, необходимое для того, чтобы величина R_ab l^al^b была неотрицательной для любого времениподобного вектора l^a, как следует из самого названия, является более сильным. Оно остается, однако, физически приемлемым в классической теории, по крайней мере в смысле средних значений. Если выполняется сильное энергетическое условие, и времениподобные геодезические, выходящие из р, снова начинают сближаться, будет существовать точка q, сопряженная точке р.

Наконец, существует общее энергетическое условие. Оно утверждает, во-первых, что справедливо сильное энергетическое условие. Во-вторых, каждая времениподобная или нулевая геодезическая включает точку, где отлична от нуля кривизна (), специально связанная со свойствами геодезической. Общее энергетическое условие не удовлетворяется для некоторых точных решений. Но эти примеры являются довольно специальными. Можно ожидать, что оно выполняется для решений, которые являются «общими» в подходящем смысле. Если общее энергетическое условие выполняется, то каждая геодезическая будет включать область гравитационного фокусирования. Отсюда вытекает, что если геодезические можно продолжить достаточно далеко в каждом направлении, то должны существовать пары сопряженных точек.

Естественно представлять себе пространственно-временную сингулярность как область, в которой кривизна становится неограниченно большой. Однако, принимая это как определение, мы сталкиваемся с проблемой, так как можно просто вырезать сингулярные точки и сказать, что остающееся многообразие и было всем пространством-временем. Поэтому лучше определить пространство-время как максимальное многообразие, на котором метрика является достаточно гладкой. Тогда можно заметить появление сингулярностей по существованию неполных геодезических, которые не могут быть продолжены на бесконечные значения аффинного параметра.

Определение сингулярностей. Пространство-время является сингулярным, если оно содержит неполные времениподобные или нулевые геодезические, но при этом не может быть вложено в большее пространство-время.

Это определение отражает наиболее объективируемые свойства сингулярностей, а именно то, что возможны частицы, история которых имеет начало и конец в конечные моменты времени. Существуют примеры, показывающие, что может возникать неполнота геодезических при остающейся ограниченной кривизне, однако считается, что в общем случае кривизна вдоль неполной геодезической будет расходиться. Это особенно важно, если пытаться с помощью квантовых эффектов решать проблемы, появляющиеся в связи с сингулярностями в классической общей теории относительности.

Между 1965 и 1970 годами Пенроуз и я использовали описанную мной технику для доказательства ряда теорем о сингулярностях. Формулировка этих теорем включает три типа условий. Во-первых, это энергетическое условие типа слабого, сильного или общего. Во-вторых, это некоторое глобальное условие на причинную структуру, например, требование отсутствия каких-либо замкнутых времениподобных кривых. Наконец, последнее условие, что в некоторых областях гравитация так сильна, что оттуда ничего не выходит наружу.

Рис. 1.10. На нормальной замкнутой поверхности выходящие с поверхности нулевые лучи расходятся, в то время как входящие лучи сходятся. На замкнутой ловушечной поверхности сближаются как входящие, так и выходящие нулевые лучи

Это третье условие можно выразить различными способами. Один способ состоит в том, чтобы предположить, что пространственное поперечное сечение Вселенной является замкнутым, так что не существует внешней области, куда можно было бы убежать. Другой состоит в утверждении, что существует так называемая замкнутая ловушечная поверхность. Это такая двумерная замкнутая поверхность, что как входящие, так и выходящие ортогональные ей нулевые геодезические будут сближаться (рис. 1.10). Обычно, если имеется сферическая двумерная поверхность в пространстве Минковского, то входящие нулевые геодезические сближаются, а выходящие — расходятся. Однако при коллапсе звезды гравитационное поле так велико, что световые конусы наклонены внутрь. Это означает, что даже выходящие нулевые геодезические сближаются друг с другом.

Ряд теорем о сингулярностях показывает, что при выполнении различных комбинаций трех типов условий пространство-время может быть неполным относительно времениподобных или нулевых геодезических. Можно ослабить одно условие, если предполагать более сильную версию двух других.

Теоремы о сингулярностях:
1. Энергетическое условие.
2. Условие на глобальную структуру.
3. Гравитация достаточно сильна для того, чтобы замкнуть определенную область.

Я проиллюстрирую это, описав теорему Хокинга-Пенроуза. Она включает общее энергетическое условие, сильнейшее из трех возможных. Глобальное условие довольно слабое и сводится к отсутствию замкнутых времениподобных геодезических. Условие невылетания берется в наиболее общем виде как существование либо ловушечной поверхности, либо замкнутой пространственноподобной трехмерной поверхности.

Рис. 1.11. Эволюция Коши D⁺(S) в будущее для множества S и ее граница в будущем — горизонт Коши H⁺(S)

Для простоты я лишь набросаю доказательство для случая замкнутой пространственноподобной трехмерной поверхности S. Можно определить эволюцию Коши в D⁺(S) в направлении будущего как область точек q, для которых каждая направленная в прошлое времениподобная геодезическая пересекает S (рис. 1.11). Тогда эволюция Коши является областью пространства-времени, которая может быть предсказана из данных на S. Теперь предположим, что эволюция Коши в будущее является компактной. Отсюда вытекает, что эволюция Коши будет иметь в будущем границу H⁺(S), называемую горизонтом Коши. С помощью рассуждений, аналогичных тем, что были использованы для границы будущего точки, можно установить, что горизонт Коши будет порождаться отрезками нулевых геодезических без конечных точек в прошлом. Однако, поскольку эволюция Коши предполагается компактной, горизонт Коши должен быть также компактным. Это означает, что генераторы нулевых геодезических будут навиваться внутри компактного множества.

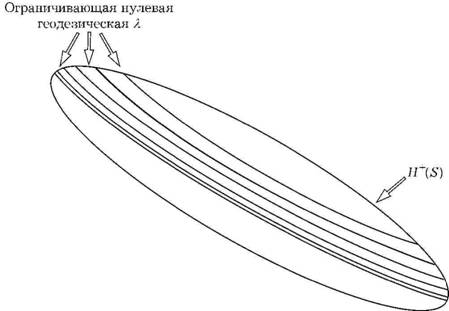
Рис. 1.12. На горизонте Коши существует предельная нулевая геодезическая λ, не имеющая конечных точек в прошлом или будущем на горизонте Коши

Они будут достигать предельной нулевой геодезической λ, которая не имеет на горизонте конечных точек в прошлом или будущем (рис. 1.12). Но если λ была бы геодезически полной, общее энергетическое условие приводило бы к тому, что она должна содержать сопряженные точки p и q. Точки на геодезической λ вне точек p и q могли бы соединяться времениподобной кривой. Но это привело бы к противоречию, поскольку на горизонте Коши не может быть двух точек, разделенных времениподобным интервалом. Следовательно, либо λ не является геодезически полной и теорема доказана, либо эволюция Коши в будущее S — некомпактное множество.

В последнем случае можно показать, что существует направленная в будущее времениподобная кривая γ из S, которая никогда не покидает эволюцию Коши для S в будущее. Аналогичные рассуждения показывают, что γ может быть продолжена в прошлое до кривой, которая никогда не покидает эволюцию Коши D-(S) в прошлое (рис. 1.13). Рассмотрим последовательность точек хп на γ, направленную в будущее, и аналогичную последовательность уп, направленную в прошлое. Для каждого значения п точки хп и уп разделены времениподобным интервалом и находятся в глобально гиперболической эволюции Коши множества S. Тогда должна существовать времениподобная геодезическая максимальной длины λn из хn к уn. Все λn будут пересекать компактную пространственно-подобную поверхность S. Это означает, что в эволюции Коши будет существовать времениподобная геодезическая λ, которая является пределом времениподобных геодезических λn (рис. 1.14). Либо λ должна быть неполной, и в этом случае теорема доказана, либо она должна содержать сопряженные точки, в силу общего энергетического условия. Но в этом случае λn будут содержать сопряженные точки при достаточно больших п. Это находится в противоречии с тем, что λn предполагались кривыми максимальной длины. Отсюда можно заключить, что пространство является неполным по отношению к нулевым или времениподобным геодезическим. Другими словами, должна существовать сингулярность.

Рис. 1.13. Если эволюция Коши в будущее (прошлое) некомпактна, то существует направленная в будущее (прошлое) времениподобная кривая из S, которая никогда не покидает эволюцию Коши в будущее (прошлое)

Рис. 1.14. Геодезическая λ, которая является пределом γn, будет неполной, потому что в противоположном случае она должна содержать сопряженные точки

Теоремы предсказывают наличие сингулярностей в двух ситуациях. Одна из них возникает в будущем при гравитационном коллапсе звезд и других массивных тел. Такие сингулярности должны возникать в конечный момент времени, по крайней мере для частиц, движущихся по неполным геодезическим. Другая ситуация, при которой предсказывается существование сингулярностей, относится к прошлому, к началу теперешнего расширения Вселенной. Это привело к отказу от попыток (делавшихся в основном русскими учеными) утверждать, что была предыдущая фаза сжатия, которая несингулярным образом сменилась расширением. Почти все специалисты сейчас убеждены, что Вселенная и само время появились в момент Большого взрыва. Это открытие является значительно более важным, чем открытие нескольких нестабильных частиц, однако не настолько важным, чтобы быть столь же щедро отмеченным Нобелевскими премиями.

Предсказание сингулярностей означает, что классическая общая теория относительности не является полной теорией. Поскольку сингулярные точки должны быть вырезаны из пространственно-временного многообразия, в них нельзя определить уравнение поля и тем самым предсказать, что произойдет с сингулярностями. Для сингулярности в прошлом, кажется, есть только один способ справиться с этой проблемой — это обратиться к квантовой гравитации. Я вернусь к этому в своей третьей лекции (глава 5). Но сингулярности, которые предсказываются в будущем, похоже, обладают одним свойством, которое Пенроуз назвал "космической цензурой". Это означает, что сингулярности проявляются в таких местах, которые, подобно черным дырам, скрыты от внешних наблюдателей. Поэтому любые нарушения предсказуемости, которые могут проявляться в этих сингулярностях, не влияют на то, что происходит во внешнем мире, по крайней мере, в соответствии с классической теорией.

Космическая цензура. Природа питает отвращение к голой сингулярности.

Однако, как я покажу в следующей лекции, в квантовой теории существует некоторая непредсказуемость. Это связано с тем, что гравитационное поле имеет внутреннюю энтропию, что является не только следствием крупнозернистой структуры. Гравитационная энтропия, а также тот факт, что время имеет начало и может иметь конец, являются темами моих следующих лекций, потому что это есть как раз то, что существенно отличает гравитацию от других физических полей.

Рис. 1.15. Коллапсирующая звезда, конформно вложенная в многообразие с границей

То, что гравитация имеет характеристику, которая ведет себя подобно энтропии, сначала был отмечен в чисто классической теории. Это зависит от предложенного Пенроузом принципа космической цензуры. Сам принцип не доказан, но считается, что он справедлив при достаточно общих начальных данных и уравнениях состояния. Я буду использовать слабую форму космической цензуры. Сделаем приближение, считая, что область в окрестности коллапсирующей звезды является асимптотически плоской. Тогда, как показал Пенроуз, можно конформно вложить пространственно-временное многообразие М в многообразие с границей M (рис. 1.15). Граница дМ будет нулевой поверхностью и будет состоять из двух компонент, нулевой бесконечности в будущем и в прошлом, называемых и . Я буду говорить, что слабая космическая цензура выполнена, если удовлетворяются два условия. Во-первых, предполагается, что нулевые геодезические генераторы в являются полными в определенной конформной метрике. Это приводит к тому, что наблюдатели, далекие от коллапса, живут до старости и на них не влияет разрыв сингулярности, исходящей от коллапсирующей звезды. Во-вторых, предполагается, что прошлое для является глобально гиперболическим. Это означает, что не существует голой сингулярности, которую можно увидеть с большого расстояния. Пенроуз использовал более сильную форму космической цензуры, которая предполагает, что пространство-время в целом является глобально гиперболическим. Но слабая форма будет вполне достаточной для моих целей.

Слабая космическая цензура.

Если слабая космическая цензура выполняется, то сингулярности, которые, как предсказано, появляются при гравитационном коллапсе, не могут быть видимыми из . Это означает, что должна существовать область пространства-времени, которая не находится в прошлом для . Эту область называют черной дырой, потому что ни свет, ни что-либо еще не может оторваться от нее и уйти на бесконечность. Границу черной дыры называют "горизонтом событий". Поскольку она так же является границей прошлого для , горизонт событий может быть получен с помощью отрезков нулевых геодезических, которые могут иметь конечную точку в прошлом, но не могут иметь каких-либо конечных точек в будущем. Из этого следует, что если слабое энергетическое условие выполнено, то генераторы горизонта не могут сближаться, т. к. если бы это происходило, они пересекались бы друг с другом на конечных расстояниях. Отсюда следует, что площадь поперечного сечения горизонта событий не может уменьшаться с течением времени, а в общем случае только увеличивается. Более того, если две черные дыры сталкиваются и сливаются вместе, площадь поверхности конечной черной дыры будет больше, чем сумма площадей поверхностей первоначальных черных дыр (рис. 1.16). Это очень похоже на поведение энтропии в соответствии со вторым законом термодинамики. Энтропия тоже никогда не может уменьшаться, и энтропия полной системы больше, чем сумма энтропий составляющих ее частей.

Рис. 1.16. Когда мы бросаем материю в черную дыру или разрешаем двум черным дырам сливаться, общая площадь горизонта событий никогда не убывает

Второй закон механики черных дыр:

Второй закон термодинамики:

Первый закон механики черных дыр:

Первый закон термодинамики:

Аналогия с термодинамикой становится еще сильнее благодаря первому закону механики черных дыр. Он связывает изменение массы черной дыры с изменением площади горизонта событий и изменениями момента импульса и электрического заряда. Можно сравнить этот закон с первым законом термодинамики, который связывает изменения во внутренней энергии с изменением энтропии и внешней работой, совершенной над системой. Нетрудно видеть, что если площадь горизонта событий аналогична энтропии, то величиной, аналогичной температуре, должно быть то, что называется "поверхностной гравитацией κ черной дыры".

Нулевой закон механики черных дыр: Для стационарных черных дыр κ одинакова во всех точках горизонта событий.

Нулевой закон термодинамики: Для систем в тепловом равновесии T везде одинакова.

Эта величина является мерой напряженности гравитационного поля на горизонте событий. Аналогия с термодинамикой еще больше увеличивается при сравнении с нулевым законом механики черных дыр: поверхностная гравитация κ одинакова на горизонте событий стационарных черных дыр.

Вдохновленный этими аналогиями, Бекенштейн (1972) предположил, что энтропия черной дыры действительно описывается некоторой величиной, кратной площади горизонта событий. Он предложил обобщенный второй закон термодинамики: сумма энтропии черной дыры и энтропии материи вне черной дыры не может уменьшаться.

Обобщенный второй закон: δ(s + сА) ≥ 0.

Рис. 1.17. Черная дыра в контакте с тепловым излучением будет поглощать часть излучения, но не может классически излучать его наружу

Однако это предположение не было самосогласовано. Если черные дыры имеют энтропию, пропорциональную площади горизонта, они также должны иметь ненулевую температуру, пропорциональную поверхностной гравитации. Рассмотрим черную дыру, которая находится в контакте с тепловым излучением при температуре ниже, чем температура черной дыры (рис. 1.17). Черная дыра будет поглощать некоторую часть излучения, но не будет способна выпускать ее из себя наружу, поскольку в соответствии с классической теорией ничто не может оторваться от черной дыры и выйти наружу. Следовательно, существует поток теплоты от теплового излучения с меньшей температурой к черной дыре с большой температурой. Это нарушает обобщенный второй закон, потому что потеря энтропии теплового излучения будет больше, чем увеличение энтропии черной дыры. Однако, как мы увидим в моей следующей лекции, согласованность восстанавливается, если заметить, что черная дыра все-таки может испускать излучение, которое является в точности тепловым. Это слишком красивый результат, чтобы оказаться простым совпадением или каким-либо приближением. Таким образом, похоже, что черные дыры действительно имеют внутреннюю гравитационную энтропию. Как я покажу, это связано с нетривиальной топологией черной дыры. Внутренняя энтропия означает, что рассмотрение гравитации вводит новый уровень непредсказуемости сверх той, которую обычно связывают с квантовой теорией. Таким образом, Эйнштейн был неправ, заявляя, что «Бог не играет в кости». Изучение черных дыр показывает, что Бог не только играет в кости, но и иногда обманывает нас, бросая их туда, где мы не можем их видеть (рис. 1.18).

Рис. 1.18.

Структура пространственно-временных сингулярностей

Роджер Пенроуз

В первой лекции Стивена Хокинга обсуждались теоремы о сингулярностях. Суть этих теорем в том, что при разумных (глобальных) физических условиях следует ожидать появления сингулярностей. Эти теоремы, конечно, ничего не говорят о природе этих сингулярностей или о том, где эти сингулярности могут быть обнаружены. С другой стороны, теоремы являются совершенно общими. Поэтому естественно спросить, какова же геометрическая природа пространственно-временных сингулярностей. Обычно предполагается, что сингулярность может быть охарактеризована расходимостью кривизны. Однако это не совсем то, что утверждают теоремы о сингулярностях сами по себе.

Сингулярности появляются в момент Большого взрыва, в черных дырах, и в момент Большого хлопка (который может восприниматься как объединение черных дыр). Они могут появляться и как голые сингулярности. В связи с этим предложен так называемый принцип космической цензуры, а именно, гипотеза, что голые сингулярности не возникают.

Чтобы объяснить идею космической цензуры, позвольте немного напомнить историю вопроса. Первым примером явного решения уравнений Эйнштейна, описывающего образование черной дыры, было решение Оппенгеймера и Снайдера (1939), описывающее коллапсирующее облако пыли. При этом существует сингулярность внутри, но она ненаблюдаема снаружи, поскольку окружена горизонтом событий. Этот горизонт представляет собой некоторую поверхность, такую, что сигналы от событий, происходящих под ней, не могут уйти на бесконечность.

Заманчиво считать, что эта картина является достаточно общей, т. е. описывает произвольный гравитационный коллапс. Однако модель Оппенгеймера-Снайдера имеет специальную симметрию (а именно, сферическую симметрию), и не очевидно, что такой пример описывает и общий случай.

Поскольку уравнения Эйнштейна в общем случае трудно решить, вместо этого можно искать те глобальные свойства, которые требуют существования сингулярностей. Например, в модели ОС имеется ловушечная поверхность, которая является поверхностью, площадь которой уменьшается вдоль световых лучей, первоначально ортогональных к ней (рис. 2.1).

Рис. 2.1. Облако пыли, коллапсирующее по Оппенгеймеру — Снайдеру, иллюстрирующее ловушечную поверхность

Можно попытаться доказать, что существование ловушечной поверхности требует существования сингулярности. (Это была первая теорема о сингулярности, которую я доказал на основе разумных предположений о причинности, не предполагая наличия сферической поверхности; см. Пенроуз 1965). Можно также вывести аналогичный результат, предполагая существование сходящегося светового конуса (Хокинг и Пенроуз 1970; этот конус появляется, когда все световые лучи, испущенные в различных направлениях из точки, начинают сходится друг к другу в какой-то последующий момент времени).

Вскоре Стивен Хокинг (1965) заметил, что в космологических масштабах можно обратить мои первоначальные аргументы, т. е. применить их к обращенной во времени ситуации. Обращение ловушечной поверхности тогда приводит к тому, что должна существовать сингулярность в прошлом (при соответствующих предположениях о причинности). При этом (обращенная во времени) ловушечная поверхность становится очень большой, соответствующей космологическим масштабам.

Рассмотрим, главным образом, ситуацию с черной дырой. Мы знаем, что где-то должна иметься сингулярность, но для того, чтобы получить черную дыру, мы должны показать, что ее окружает горизонт событий. Гипотеза космической цензуры утверждает именно это, т. е. то, что сингулярность нельзя увидеть снаружи. В частности, из этой гипотезы следует, что должна существовать некоторая область, из которой невозможно отправить сигналы на внешнюю бесконечность. Границей этой области является горизонт событий. Мы можем также использовать теорему о границе, изложенную Стивеном в своей лекции и состоящую в том, что горизонт событий является границей прошлого для будущей нулевой бесконечности. Следовательно, мы знаем, что эта граница:
• должна быть нулевой поверхностью, которая является гладкой и генерируется нулевыми геодезическими;
• содержит неограниченную в будущем нулевую геодезическую, исходящую из каждой точки, в которой отсутствует условие гладкости, и что
• площадь пространственных сечений не может уменьшаться со временем.

Кроме того, было показано (Израэль 1967, Картер 1971, Робинсон 1975, Хокинг 1972), что асимптотическим пределом такого пространства-времени в будущем является пространство-время Керра. Это примечательный результат, поскольку метрика Керра является очень интересным точным решением эйнштейновских уравнений в вакууме. Поскольку это утверждение связано с таким вопросом, как энтропия черной дыры, я собираюсь к нему вернуться в следующей лекции (глава 4).

Поэтому мы действительно имеем нечто, качественно подобное решению ОС. Некоторое отличие, а именно то, что мы приходим к решению Керра, а не Шварцшильда, довольно несущественно. Главное, что картины в этих случаях похожи.

Однако более точные рассуждения основаны на гипотезе космической цензуры. Фактически, космическая цензура очень важна, поскольку теория целиком от нее зависит, и без нее мы вместо черной дыры увидели бы жуткие вещи. Поэтому действительно следует спросить себя, является ли эта гипотеза истинной. Долгое время я считал, что она может быть неверной, и предпринимал различные попытки найти контрпримеры (Стивен Хокинг однажды заявил, что тот факт, что я попытался доказать ложность гипотезы космической цензуры и не преуспел в этом, является одним из сильнейших аргументов в пользу этой гипотезы. Однако я думаю, что это очень слабый аргумент!)

Я хочу обсудить принцип космической цензуры в контексте определенных идей, касающиющихся идеальных точек пространства-времени. (Эти понятия появились в работах Зейферта 1971 и Героха, Кронхаймера и Пенроуза 1972.) Основная идея состоит в том, что в пространство-время мы должны включать как действительно «сингулярные» точки, так и точки «на бесконечности», называемые идеальными точками. Введем сначала понятие НП, неразложимого множества прошлого. Здесь под «множеством прошлого» я понимаю множество, которое содержит свое собственное прошлое, а «неразложимое» означает, что его нельзя разделить на два «множества прошлого» таким образом, чтобы одно содержало другое. Существует теорема, которая утверждает, что любое НП можно описать как прошлое некоторой времениподобной кривой (рис. 2.2).

Рис. 2.2. Множество прошлого, СНП, ННП

Существует две категории НП, а именно СНП и ННП. СНП — это собственное НП, т. е. прошлое некоторой точки пространства-времени. ННП — несобственное НП, не являющееся прошлым реальной точки пространства-времени. Иными словами, ННП определяют будущие идеальные точки. Кроме того, можно различать ННП по тому, находится ли идеальная точка «на бесконечности» (и в этом случае существует времениподобная кривая, генерирующая НП бесконечной собственной длины), т.е. является ∞-ННП, или она является сингулярностью или сингулярным ННП (в этом случае любая генерирующая ее времениподобная кривая имеет конечную собственную длину). Очевидно, все эти понятия могут быть применены не только к множествам прошлого, но и к множествам будущего. В этом случае мы получаем неразложимые множества будущего (НБ), которые можно разделить на СНБ и ННБ, а последние в свою очередь разложить на ∞-ННБ и сингулярные ННБ. Заметим также, что для того, чтобы эти понятия заработали, следует предположить отсутствие замкнутых времениподобных кривых, на самом деле, достаточно наложить существенно более слабое условие, что не существует двух точек, имеющих одинаковое будущее и одинаковое прошлое.

Как описать на этом языке голые сингулярности и гипотезу космической цензуры? Во-первых, гипотеза космической цензуры не должна исключать Большого взрыва (в противном случае это будет большим ударом для космологов). Все вещи всегда возникают из Большого взрыва и никогда не попадают в него обратно. Поэтому можно попытаться определить голую сингулярность как нечто, куда может входить и откуда может выходить времениподобная кривая. Тогда проблема Большого взрыва автоматически снимается, поскольку этот взрыв не относится к голой сингулярности. Теперь можно определить голую ННП, как ННП, которое содержится в СНП. Это существенно локальное определение, т. е. мы не требуем, чтобы наблюдатель находился на бесконечности. Оказывается, можно показать (Пенроуз 1979), что запрет на голые ННП в пространстве-времени определяется тем же условием, если в этом определении заменить слово «прошлое» на слово «будущее» (запрет на голые ННБ).

Гипотеза, что такие голые ННП (или, эквивалентно, ННБ) не возникают в общем пространстве-времени, называется гипотезой сильной космической цензуры. Ее интуитивный смысл состоит в том, что сингулярная точка (или бесконечная точка) — в данном случае ННП — не может просто «появиться» в середине пространства-времени таким образом, чтобы быть «видимой» из некоторой конечной точки — вершины данной СНП. Существенно, что наблюдатель не должен находиться на бесконечности, поскольку для данного пространства-времени мы можем не знать, что действительно является бесконечностью. Кроме того, если бы принцип сильной космической цензуры нарушался, мы могли бы за конечное время наблюдать частицу, попадающую в сингулярность, где законы физики перестают выполняться (или достигать бесконечности, что не лучше). Можно высказать и гипотезу слабой космической цензуры — следует просто заменить СНП на ∞-ННП. Гипотеза сильной космической цензуры требует, чтобы общее пространство-время с материей, подчиняющейся разумным уравнениям состояния (для примера — вакуум), могло быть расширено на пространство-время, свободное от голых сингулярностей (голых сингулярных ННП).

Оказывается (Пенроуз 1979), можно утверждать, что исключение голых ННП эквивалентно глобальной гиперболичности или тому, что пространство-время целиком есть область, определяемая некоторой поверхностью Коши (Герох 1970). Заметим, что эта формулировка сильной космической цензуры является явно симметричной по времени: можно поменять местами прошлое и будущее, если поменять местами НП и НБ.

В общем случае нужны дополнительные условия, чтобы исключить молнии. Под молнией мы понимаем сингулярность, которая достигает нулевой бесконечности, разрушая пространство-времени по мере продвижения (см. Пенроуз 1978, рис. 2.7). Это не требует нарушения принципа космической цензуры. Существует более сильная версия этого принципа (Пенроуз 1978, условие СС4), учитывающая возможность молний.

Вернемся к вопросу о том, справедлива ли гипотеза о космической цензуре. Во-первых, заметим, что, возможно, она не выполняется в квантовой гравитации. В частности, взрыв черных дыр (о которых Стивен Хокинг будет говорить чуть позднее) приводит к ситуациям, где космическая цензура кажется нарушенной.

В классической общей теории относительности существуют различные результаты в обоих направлениях. В одной из попыток опровергнуть космическую цензуру я получил неравенства, которые должны выполняться, если космическая цензура справедлива (Пенроуз 1973). Они действительно оказались правильными (Гиббон 1972). Это дает некоторую поддержку идее о существовании чего-то подобного космической цензуре. Отрицательным аргументом является наличие некоторых частных примеров (которые, впрочем, нарушают принцип универсальности) и некоторые обрывки численных результатов, против которых существует много различных возражений. К тому же есть некоторые свидетельства, о которых я узнал только недавно — фактически Гари Горовиц рассказал мне о них только вчера — что некоторые из вышеупомянутых неравенств несправедливы, если космологическая постоянная положительна. Лично я всегда был убежден, что космологическая постоянная должна быть равна нулю, однако будет очень интересно, если справедливость космической цензуры окажется зависящей от неположительности этой постоянной. В частности, может существовать интригующая связь между природой сингулярностей и природой бесконечности. Бесконечность пространственноподобна, если космологическая постоянная положительна, и нулевая, если постоянная равна нулю. Соответственно, сингулярности могут иногда оказываться времениподобными (т.е. голыми, нарушающими космическую цензуру), если космологическая постоянная положительна, но возможно, что сингулярности не могут быть времениподобными (т.е. удовлетворяют космической цензуре), если постоянная равна нулю.

Для обсуждения времениподобной или пространственно-подобной природы сингулярностей разберемся сначала с соотношениями причинности между НП. Обобщая причинность между точками, мы можем сказать, что НП A причинно предшествует НП B, если A Ì B; A хронологически предшествует B, если существует СНП P такое, что A Ì P Ì В. Мы будем говорить, что А и В пространственноподобно разделены, если ни одна из них причинно не предшествует другой (рис. 2.3).

Рис. 2.3. Соотношения причинности между различными НП: 1) А причинно предшествует В; 2) А хронологически предшествует В; 3) А и В пространственноподобно разделены

Условие сильной космической цензуры можно тогда выразить, сказав, что сингулярности никогда не бывают времениподобными. Пространственноподобные (или нулевые) сингулярности могут быть либо прошлого, либо будущего типа. Отсюда, если сильная космическая цензура выполняется, сингулярности разделяются на два класса:
(П) прошлого типа, определенные как ННП;
(Б) будущего типа, определенные как ННБ.

Голые сингулярности могут объединять эти две возможности в одну, так что голая сингулярность может быть ННБ и ННП одновременно. Следовательно, реальным следствием космической цензуры является разделение этих классов. Типичными примерами класса (Б) являются сингулярности в черных дырах и Большой хлопок (если он существует), а в класс (П) входит Большой взрыв и белые дыры (если они существуют). В действительности, я не верю, что Большой хлопок реально может произойти (по идеологическим причинам, к которым я вернусь в последней лекции), и тем более считаю невозможным существование белых дыр, поскольку они не подчиняются второму закону термодинамики.

Возможно, что два типа сингулярностей подчиняются совершенно разным законам. Может быть, законы квантовой гравитации будут для них совершенно различны. Я думаю, что Стивен Хокинг здесь не согласится со мной [Хокинг: «Да!»], но я считаю следующие факты свидетельством этого утверждения:
1) второй закон термодинамики;
2) наблюдения ранней Вселенной (например, результаты космического аппарата СОВЕ), показывающие, что она была очень однородной;
3) существование черных дыр (фактически уже наблюдаемых).

Из (1) и (2) можно утверждать, что сингулярность Большого взрыва была чрезвычайно однородна, и из (1) следует, что она была свободна от белых дыр (белые дыры очень сильно нарушают второй закон термодинамики). Тогда для сингулярностей черных дыр должны выполняться совершенно другие законы (3). Чтобы описать эту разницу более точно, отметим, что кривизна пространства-времени описывается тензором Rabcd Римана, который является суммой тензора Вейля Cabcd (описывающего приливные искажения, которые в первом порядке малости сохраняют неизменным объем) и тензором Риччи Rab (умноженным на матрицу gcd с должным образом зацепленными индексами), который описывает искажения, связанные с уменьшением объема (рис. 2.4).

Рис. 2.4. Эффекты ускорения из-за наличия пространственновременной кривизны: (1) приливное искажение вследствие вейлевской кривизны; (2) эффект уменьшения объема из-за кривизны Риччи

В стандартных космологических моделях (Фридмана, Леметра, Робертсона и Уолкера, см., например, Риндлер 1977) в момент Большого взрыва тензор Вейля равнялся нулю. Существует также обратное утверждение, доказанное Р. Ньюменом, по которому Вселенная с начальной сингулярностью конформно-регулярного типа с нулевым тензором Вейля обязана при выполнении подходящего уравнения состояния быть Вселенной Фридмана-Деметра-Робертсона-Уолкера; (см. Ньюмен 1993). С другой стороны, сингулярности черных/белых дыр имеют (в общем случае) расходящийся тензор Вейля. Это говорит о следующем:
Гипотеза вейлевской кривизны
• Сингулярности начального типа (П) ограничены равенством нулю тензора Вейля.
• Сингулярности конечного типа (Б) ничем не ограничены.

Это очень близко к тому, что мы наблюдаем. Если Вселенная замкнута, конечная сингулярность (Большой хлопок) будет иметь расходящийся тензор Вейля, в открытой Вселенной рождающиеся черные дыры тоже имеют расходящийся тензор Вейля (см. рис. 2.5).

Рис. 2.5. Гипотеза вейлевской кривизны: первоначальные сингулярности (Большой взрыв) ограничены условиями обращения в нуль вейлевской кривизны, в то время как для конечных сингулярностей следует ожидать расходимости вейлевской кривизны

Дальнейшую поддержку эта гипотеза находит в том, что существует ограничение, согласно которому для того, чтобы ранняя Вселенная была достаточно гладкой и свободной от белых дыр, ее фазовое пространство должно определяться множителем по крайней мере порядка (Эта цифра соответствует возможному объему фазового пространства черной дыры с 1080 барионами, как это следует из формулы Бекенштейна-Хокинга для энтропии черной дыры — см. Бекенштейн 1972, Хокинг 1975 — и тому, что Вселенная имеет по крайней мере такое количество материи).

Вопросы и ответы

Вопрос: Считаете ли Вы, что квантовая гравитация устранит сингулярности?

Ответ: Я не думаю, что это будет именно так. Если бы это было так, то Большой взрыв возник бы из предварительно существовавшей коллапсирующей фазы. Мы должны спросить себя, как могла эта предварительная фаза возникнуть с такой малой энтропией. Эта картина приносит в жертву лучшую возможность для объяснения второго закона термодинамики. Более того, сингулярности коллапсирующих и расширяющихся вселенных будут иметь между собой в этом случае что-то общее, в то время как, похоже, они имеют чрезвычайно различные геометрии. Истинная теория квантовой гравитации должна заменить наши сегодняшние представления о пространстве-времени в сингулярностях. Она должна дать ясный и четкий способ рассмотрения того, что в классической теории мы называем сингулярностями. И она не должна быть просто несингулярным пространством-временем, а чем-то совершенно другим.

Квантовые черные дыры

Стивен Хокинг

В своей второй лекции я хочу поговорить о квантовой теории черных дыр. Мне кажется, что она ведет к новому уровню непредсказуемости в физике сверх обычной неопределенности, связанной с квантовой механикой. Это происходит потому, что черные дыры имеют внутреннюю энтропию, что приводит к потере информации из нашей области Вселенной. Должен сказать, что эти утверждения являются спорными: многие люди, работающие в квантовой гравитации, включая почти всех, кто пришел туда из физики частиц, будут инстинктивно отвергать идею о том, что информация о квантовом состоянии системы может быть утеряна. Однако все эти ученые достигли весьма скромных успехов, пытаясь показать, как можно извлечь информацию из черной дыры. Я уверен, что в конце концов они будут вынуждены принять мое утверждение о том, что информация теряется, как раньше вынуждены были согласиться с тем, что черные дыры излучают, хотя это находится в полном противоречии со всеми их убеждениями.

Начну с напоминания классической теории черных дыр. В прошлой лекции мы видели, что гравитация всегда действует как притягивающая сила, по крайне мере, в нормальной ситуации. Если бы гравитация иногда действовала как притягивающая, а иногда — как отталкивающая сила, как в электродинамике, мы не замечали бы ее вообще, потому что гравитационная сила в 10⁴⁰ раз слабее электромагнитных сил. Только благодаря тому, что гравитационные силы между частицами двух макроскопических тел, подобных нашим телам и Земле, складываются, они приводят к силе, величину которой мы можем почувствовать.

То, что гравитация всегда является притягивающей силой, означает, что она старается собрать вместе всю материю во Вселенной, чтобы образовать объекты, подобные звездам и галактикам. В течение некоторого времени эти объекты удерживаются от дальнейшего сжатия за счет теплового давления, в случае звезд, или вращения и внутреннего движения, в случае галактик. Однако в конце концов теплота и момент импульса рассеиваются, и объект начинает сжиматься. Если масса объекта меньше 1,5 масс Солнца, сжатие может быть остановлено за счет давления вырожденного газа электронов или нейтронов. Тогда образуется белый карлик или нейтронная звезда, соответственно. Однако, если масса больше указанного предела, то не существует ничего, что могло бы остановить неудержимое сжатие. После того, как тело сожмется до определенного критического размера, гравитационное поле на его поверхности становится настолько сильным, что световые конусы оказываются наклоненными внутрь этой поверхности, как на рис. 3.1.

Рис. 3.1. Пространственно-временная картина коллапса звезды с образованием черной дыры. Показан горизонт событий и замкнутая ловушечная поверхность

Я предпочел бы нарисовать четырехмерную картину, однако в результате урезания бюджета Кембриджский университет может позволить себе только двумерные экраны. Поэтому в вертикальном направлении я буду показывать время, а два из трех пространственных направлений буду изображать с помощью перспективы. Вы можете видеть, что даже выходящие световые лучи наклонены друг к другу и поэтому они не расходятся, а сближаются. Это означает, что существует замкнутая ловушечная поверхность, наличие которой является одной из возможных формулировок третьего условия теоремы Хокинга-Пенроуза.

Если верна гипотеза космической цензуры, то она предсказывает, что ловушечная поверхность и сингулярность не могут быть видны с большого расстояния. Тогда должна существовать такая область пространства-времени, из которой невозможно уйти на бесконечность. Эту область называют черной дырой. Ее граница называется горизонтом событий. Она является нулевой поверхностью, образованной теми световыми лучами, которые как раз не смогли уйти на бесконечность. Как мы видели в последней лекции, площадь поперечного сечения горизонта событий не может уменьшаться, по крайней мере в классической теории. Это, а также расчеты сферического коллапса по теории возмущений наводят на мысль, что черные дыры находятся в стационарном состоянии. Теорема «об отсутствии волос» у черной дыры, доказанная в совместной работе Израэли, Картера, Робинсона и моей, показывает, что только стационарные черные дыры в отсутствии материальных полей могут соответствовать решениям Керра. Они характеризуются двумя параметрами, массой Μ и моментом импульса J. Теорема об отсутствии волос была распространена Робинсоном на случай наличия электромагнитного поля. Это добавляет третий параметр Q, электрический заряд. Теорема об отсутствии волос не доказана для случая полей Янга-Миллса, но, похоже, единственной разницей будет добавление одного или нескольких целых чисел, нумерующих дискретное семейство нестабильных решений. Можно показать, что в случае независящих от времени черных дыр, описываемых уравнениями Эйнштейна-Янга-Миллса, не существует других непрерывных степеней свободы.

Теорема об отсутствии волос. Стационарные черные дыры характеризуются массой М, моментом импульса J и электрическим зарядом Q

Теорема об отсутствии волос показывает, что при коллапсе тела с образованием черной дыры теряется огромное количество информации. Коллапсирующее тело описывается очень большим числом параметров. Существуют различные типы материи и мультипольные моменты распределения масс. Однако образующая черная дыра полностью не зависит от типа материи и быстро теряет все мультипольные моменты, за исключением первых двух: монопольного момента — массы и дипольного момента, соответствующего моменту импульса.

Такая потеря информации несущественна в рамках классической теории. Можно сказать, что вся информация о коллапсирующем теле просто остается внутри черной дыры. Поэтому внешнему наблюдателю было бы очень трудно определить, на что похоже коллапсирующее тело. Однако в классической теории это все же хотя бы в принципе возможно. В действительности наблюдатель никогда не теряет коллапсирующее тело из поля зрения. По мере приближения к горизонту событий он наблюдает замедление коллапса и потускнение света. Но при этом наблюдатель все еще может видеть, из чего было сделано тело и как распределена масса. Однако квантовая теория все это меняет. Во-первых, до того, как коллапсирующее тело пересечет горизонт событий, оно испустит лишь ограниченное число фотонов. Их будет недостаточно для того, чтобы перенести всю информацию о коллапсирующем теле. Это означает, что в квантовой теории отсутствует возможность измерения состояния коллапсирующего тела внешним наблюдателем. Можно было бы не считать этот вопрос чересчур важным, поскольку информация все равно остается внутри черной дыры, даже если она не может быть измерена снаружи. Но именно здесь проявляется второй эффект квантовой теории по отношению к черным дырам. Как я покажу, квантовая теория является причиной того, что черные дыры излучают и теряют массу. Представляется, что они в конце концов полностью исчезают, унося с собой всю информацию, которая была внутри. Я приведу аргументы, которые показывают, что информация действительно теряется и не может быть возвращена в какой-либо форме. Как я покажу, эта потеря информации приводит к новому уровню неопределенности в физике, стоящей над обычной неопределенностью, связанной с квантовой теорией. К сожалению, в противоположность принципу неопределенности Гейзенберга, этот дополнительный уровень неопределенности в случае черных дыр, видимо, будет значительно сложнее подтвердить экспериментально. Но я покажу в третьей лекции (глава 5), что мы в определенном смысле уже наблюдали эту неопределенность при измерениях флуктуаций микроволнового реликтового излучения.

Тот факт, что квантовая теория является причиной излучения черных дыр, был впервые открыт при изучении квантовой теории поля на фоне коллапсирующей черной дыры. Чтобы увидеть, как это получается, полезно использовать картинки, обычно называемые диаграммами Пенроуза. Однако я думаю, что сам Пенроуз согласится с тем, что на самом деле они должны называться диаграммами Картера, поскольку именно Картер начал их систематически использовать. При сферическом коллапсе пространство-время не зависит от углов θ и φ. Вся геометрия описывается в r – t плоскости. Поскольку любая двумерная поверхность является конформной плоскому пространству, можно представить причинную структуру с помощью диаграммы, на которой нулевые линии в r – t плоскости наклонена под углами ±45° к вертикали.

Рис. 3.2. Диаграмма Картера —Пенроуза для пространства Минковского поверхность

Начнем с плоского пространства Минковского, для которого диаграмма Картера-Пенроуза имеет вид треугольника, поставленного на один угол (рис. 3.2). Две боковые стороны справа соответствуют нулевым бесконечностям прошлого и будущего, которые обсуждались в моей первой лекций. Они реально находятся на бесконечности, но при приближении к нулевым бесконечностям будущего и прошлого все расстояния сжимаются с помощью конформного множителя. Каждая точка этого треугольника соответствует 2-сфере радиусом r. На вертикальной линии слева r = 0, и эта линия представляет центр симметрии. Правая сторона диаграммы соответствует r → ∞.

Рис. 3.3. Диаграмма Картера-Пенроуза для звезды, которая коллапсирует с образованием черной дыры

Из диаграммы нетрудно видеть, что каждая точка в пространстве Минковского находится в прошлом для нулевой бесконечности будущего . Это означает, что черная дыра и горизонт событий отсутствуют. Однако если имеется сферическое коллапсирующее тело, то вид диаграммы существенно меняется (рис. 3.3). Она выглядит так же в прошлом, но теперь верх треугольника обрезан и заменен на горизонтальную границу. Это та сингулярность, которую предсказывает теорема Хокинга-Пенроуза. Теперь можно видеть, что существуют точки под этой горизонтальной линией, которые не лежат в прошлом нулевой бесконечности будущего . Другими словами, существует черная дыра. Горизонт событий, граница черной дыры, изображается диагональной линией, которая идет вниз из правого верхнего угла и пересекается с вертикальной линией, соответствующей центру симметрии.

На фоне коллапсирующего объекта можно рассмотреть скалярное поле φ. Если бы метрика пространства-времени не зависела от времени, то решение волнового уравнения, содержащее только положительные частоты на , содержало бы эти частоты и на . Это означало бы, что там не происходит рождение частиц, и если первоначально частиц на не было, то не было бы и уходящих частиц.

Однако про коллапсе метрика зависит от времени. Это приводит к тому, что положительно-частотное на решение приобретает отрицательные частоты, приходя на . Можно рассчитать это смешивание, если взять волну с временной зависимостью на и рассмотреть ее распространение обратно на . Если это сделать, то обнаруживается, что часть волны, которая прошла вблизи горизонта, получила сильное голубое смещение. Примечательно, что, обращая эти рассуждения, можно найти, что смешивание не зависит от деталей коллапса в более поздние времена. Оно зависит только от величины поверхностной гравитации , которая измеряет напряженность гравитационного поля на горизонте черной дыры. Смешивание положительных и отрицательных частот приводит к рождению частиц. 

Когда я впервые изучал этот эффект в 1973 г., я ожидал, что обнаружу во время коллапса взрывное излучение, но после этого рождение частиц должно было бы затухнуть, и черная дыра действительно стала бы черной. К моему большому удивлению, я обнаружил, что после первоначального взрыва во время коллапса продолжается рождение частиц и их излучение с постоянной скоростью. Более того, излучение оказалось тепловым с температурой . Это было именно то, что требовалось, чтобы сделать самосогласованной идею о том, что черная дыра имеет энтропию, пропорциональную площади ее горизонта событий. Более того, в этом случае фиксируется константа пропорциональности, которая оказывается равной одной четверти в планковских единицах, в которых G = с = = 1. В такой системе площадь равна 10 ^–66 см², так что черная дыра с массой, равной массе Солнца, будет иметь энтропию порядка 10⁷⁸. Эта величина отражает то колоссальное число различных способов, которыми может быть создана черная дыра.

Тепловое излучение черной дыры 

Когда я пришел к открытию излучения черных дыр, казалось чудом, что довольно неаккуратные вычисления приводят к излучению, которое в точности является тепловым. Однако в совместной работе с Джимом Хартлем и Гарри Гиббонсом были найдены глубокие причины этого. Чтобы их объяснить, я начну с примера метрики Шварцшильда.

Метрика Шварцшильда 

Эта метрика соответствует гравитационному полю, которое создает невращающаяся черная дыра. В обычных координатах r и t эта метрика обладает кажущейся особенностью при шварцшильдовском радиусе r = 2М. Однако эта особенность является лишь следствием плохого выбора координат. Можно выбрать другие координаты, в которых метрика в этой точке будет регулярной.

Диаграмма Картера-Пенроуза имеет вид ромба, со срезанными верхом и низом (рис. 3.4). Она делится на четыре области двумя нулевыми поверхностями, на которых r = 2М. Область справа, отмеченная на диаграмме как является асимптотически плоским пространством, в котором, как мы полагаем, мы и живем. Она имеет нулевые бесконечности и в прошлом и в будущем, подобно плоскому пространству-времени. С левой стороны диаграммы существует другая асимптотически плоская область , которая, по-видимому, соответствует другой вселенной, связанной с нашей только горловиной. Однако, как мы увидим, она связана с нашей областью с помощью мнимого времени. Нулевая поверхность, идущая снизу слева вверх направо, является границей области, из которой можно уйти на правую бесконечность. Поэтому она является горизонтом событий будущего, причем эпитет «будущий» добавлен для того, чтобы отличать его от горизонта событий прошлого, идущего снизу справа вверх налево.

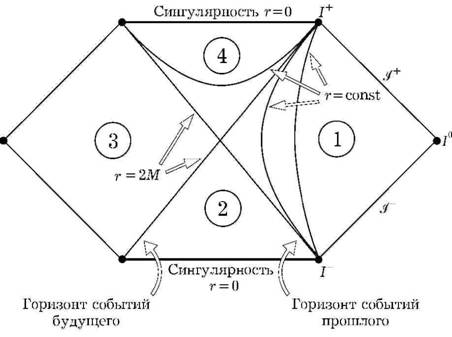
Рис. 3.4. Диаграмма Картера —Пенроуза для вечно существующей шварцшильдовской черной дыры

Вернемся теперь к метрике Шварцшильда в первоначальных координатах r и t. Если положить t = iτ, получается положительно определенная метрика. Я буду называть такие метрики евклидовыми, хотя они могут соответствовать искривленному пространству. В такой евклидово-шварцшильдовской метрике по-прежнему существует кажущаяся сингулярность при r = 2М. Однако можно определить новую радиальную координату х, равную 4M (l – 2Mr^–1)^1/2.

Евклидово — шварцшильдовская метрика

Метрика в плоскости x-τ становится тогда подобна метрике в полярной системе координат, если сопоставить координату τ с периодом 8πΜ. Аналогично, другие евклидовы метрики для черной дыры будут иметь кажущиеся сингулярности на своих горизонтах, которые могут быть устранены сопоставлением мнимой временной координаты с периодом (рис. 3.5).

Рис. 3.5. Евклидово —шварцшильдовское решение, в котором τ выбрано периодическим

В чем состоит смысл использования мнимого времени, отождествленного с некоторыми периодом β? Чтобы это увидеть, рассмотрим амплитуду перехода из некоторой конфигурации поля φ₁ на поверхности t₁ в конфигурацию φ₂ на плоскости t₂- Она дается матричным элементом оператора . Однако ее можно также представить с помощью интеграла по путям по всем полям φ в интервале времени между t₁ и t₂, которые совпадают с данными полями φ₁ и φ₂ на двух поверхностях (рис. 3.6).

Рис. 3.6. Амплитуда перехода из состояния φ₁ в момент времени t₁ в состояние φ₂, заданное в момент времени t₂

Выберем интервал времени (t₁ – t₂) чисто мнимым и равным β (рис. 3.7). Можно также считать начальное поле φ₁ равным конечному полю φ₂ и просуммировать по полному базису состояний φ_n. Тогда с левой стороны получаем среднее значение , просуммированное по всем состояниям. Это выражение совпадает с термодинамической статистической суммой Ζ при температуре .

Рис. 3.7. Статистическая сумма при температуре T может быть представлена как интеграл по путям по всем полям в евклидовом пространстве-времени с периодом β = T~ по мнимому времени

С правой стороны уравнения записан интеграл по путям. Положим в нем φ₁ = φ₂ и просуммируем по всем конфигурациям поля φ_n. Это означает, что эффективно происходит вычисление интеграла по путям по всем полям φ в пространстве-времени, которое обладает периодичностью по мнимому времени с периодом β. Такая статистическая сумма для полей φ при температуре τ дается интегралом по путям по всем полям в евклидовым пространстве-времени. Это пространство-время периодично по мнимому времени с периодом β = T^–1.

Если вычислить интеграл по путям в плоском пространстве-времени, обладающем периодом β по мнимому времени, можно получить обычный результат для статистической суммы излучения черного тела. Однако, как мы уже видели, евклидово-шварцшильдовское решение является также периодическим в мнимом времени с периодом . Это означает, что поля на фоне решения Шварцшильда ведут себя так, как если бы они находились в состоянии теплового равновесия с температурой .

Периодичность в мнимом времени объясняет, почему запутанные вычисления смешивания решений с разными частотами привели к излучению, которое находится в тепловом равновесии. Однако такой вывод обходит проблему вклада очень высоких частот, которые следует учитывать в подходе смешивания решений с разными частотами. Он может быть использован в том случае, когда существует взаимодействие между квантовыми полями на заданном фоне. Фактически то, что интеграл по путям вычисляется на периодическом фоне, приводит к тому, что все физические величины типа средних значений будут соответствовать состояниям теплового равновесия. Это было бы очень трудно установить в подходе со смешиванием частот.

Можно даже расширить эти взаимодействия, чтобы учесть взаимодействия непосредственно с гравитационным полем. Начнем с фоновой метрики g₀, такой как евклидово-шварцшильдовская метрика, являющаяся решением классических уравнений поля. Действие I можно разложить в степенной ряд по возмущениям δg вблизи g₀: 

При этом линейное слагаемое обращается в нуль в силу того, что g₀ является решением полевых уравнений. Квадратичные слагаемые можно воспринимать как описание гравитонов на заданном фоне, в то время как кубичное и более высокие слагаемые в разложении описывают взаимодействие между гравитонами. Интеграл по путям по квадратичным слагаемым является конечным. В чисто гравитационной теории существуют неперенормируемые расходимости в двухпетлевых диаграммах, но в теориях супергравитации они сокращаются со вкладом фермионов. Неизвестно, имеют ли теории супергравитации расходимости в трех и более петлях, поскольку до сих пор не нашлось никого, кто был бы достаточно отважен или безрассуден, чтобы проделать эти вычисления. В ряде последних работ есть указания на то, что эти теории могут быть конечны во всех порядках. Но даже если существуют расходимости в высших петлях, они дадут очень малые отличия, за исключением случая, когда фоновая метрика соответствует искривлению на масштабах длины Планка, т.е. 10^–33 см.

Более интересным по сравнению со слагаемыми высшего порядка является слагаемое нулевого порядка, а именно, действие с фоновой метрикой g₀:

Обычное действие Эйнштейна-Гильберта в общей теории относительности является объемным интегралом от скалярной кривизны R. Она равна нулю для вакуумных решений, так что можно считать, что действие для евклидово-шварцшильдовского решения равно нулю. Однако в действии существует также поверхностное слагаемое, пропорциональное интегралу от К, т.е. от следа второй квадратичной формы на граничной поверхности. Если учесть это слагаемое и вычесть из него поверхностное слагаемое для плоского пространства, можно найти, что действие с евклидово -шварцшильдовской метрикой равно , где β — период по мнимому времени на бесконечности. Тогда доминирующий вклад в интеграл по путям для статистической суммы Ζ paвен exp : 

Дифференцируя ln Z по периоду β, можно получить среднее значение энергии или, другими словами, массу: 

Таким образом находим, что масса . Это подтверждает уже известную связь между массой и периодом, или обратной температурой Вселенной. Однако можно продвинуться дальше. Следуя стандартным термодинамическим рассуждениям, логарифм статистической суммы равен взятой с обратным знаком свободной энергии F, деленной на температуру Т: 

Но свободная энергия равна массе или энергии плюс произведение температуры на энтропию S: 

F=(E)- TS. 

Собирая все вместе, нетрудно видеть, что действие для черной дыры дает энтропию 4πΜ ² : 

Это именно то, что требуется для того, чтобы законы черных дыр стали полным аналогом законов термодинамики.

Откуда берется внутренняя гравитационная энтропия, не имеющая аналогов в других квантовых теориях поля? Причина ее появления в том, что гравитация допускает различные топологии пространственно-временного многообразия. В случае, который мы рассматриваем, евклидово-шварцшильдовское решение имеет границу на бесконечности с топологией S² x S¹.

Рис. 3.8. Бесконечно удаленная граница для евклидово-шварцшильдовского решения 

Поверхность S² — это большая пространственноподобная 2-сфера на бесконечности, a S¹ соответствует направлению мнимого времени, концы которого периодически отождествлены (рис. 3.8). Можно вложить в эту границу метрики по крайней мере с двумя разными топологиями. Одна, конечно, евклидово-шварцшильдовская метрика с топологией R² x S², т.е. евклидова 2-плоскость, умноженная на 2-сферу. Другая — это R³ x S¹, т.е. топология евклидового плоского пространства с периодически отождествленными в направлении мнимого времени границами. Эти топологии имеют различные характеристики Эйлера. Эйлерова характеристика периодически отождествленного плоского пространства равна нулю, в то время как для евклидово-шварцшильдовского решения — двум. 

Смысл всего этого состоит в следующем: на топологии периодически отождествленного плоского пространства можно найти периодическую функцию времени т, градиент которой нигде не обращается в нуль и которая согласована с координатой мнимого времени на бесконечности. Тогда можно составить действие для области между поверхностями τ₁ и τ₂. 

При этом получается два вклада в действие: объемный интеграл от лангражиана для материи и лагранжиана Эйнштейна-Гильберта и поверхностное слагаемое. Если решение не зависит от времени, то поверхностное слагаемое при τ = τ₁ будет сокращаться со слагаемым при τ = τ₂. Тогда реальный вклад в поверхностное слагаемое появится только от границы на бесконечности. Это дает половину массы, умноженной на интервал мнимого времени (τ₂ – τ₁). Если масса ненулевая, то должны быть создающие массу ненулевые поля материи. Можно показать, что интеграл по объему от лагранжиана полей материи и лагранжиана Эйнштейна-Гильберта также дает 1/2М(τ₂ – τ₁). Тогда полное действие равно Μ(τ₂ – τ₁) (рис. 3.9). Если подставить этот вклад в логарифм статистической суммы в термодинамической формуле, можно найти, что среднее значение энергии равно массе, как и следовало ожидать. Однако вклад в энтропию от фоновых полей будет равен нулю.

Рис. 3.9. Действие для периодически отождествленного евклидового плоского пространства равно Μ(τ₂ – τ₁)

Рис. 3.10. Полное действие для евклидово-шварцшильдовского действия равное , без учета вклада от угла для r = 2M 

Ситуация несколько отличается для евклидово-шварцшильдовского решения. Поскольку характеристика Эйлера равна не нулю, а двум, невозможно найти такую функцию времени τ, градиент которой был бы повсюду отличен от нуля. Лучшее, что можно сделать — это выбрать координату мнимого времени в решении Шварцшильда. Оно имеет на горизонте фиксированную 2-сферу, на которой τ ведет себя подобно угловой переменной. Если теперь вычислить действие между двумя поверхностями τ = const, объемный интеграл обратится в нуль, поскольку поля материи отсутствуют, и скалярная кривизна равна нулю. Поверхностное слагаемое со следом К на бесконечности снова дает . Однако теперь существует и другое поверхностное слагаемое на горизонте, когда поверхности τ₁ и τ₂ пересекаются в угле. Можно вычислить этот вклад и найти, что он также равен (рис. 3.10). Поэтому полное действие для области между τ₁ и τ₂ равно Μ (τ₂ – τ₁).

Если использовать это действие, положив τ₂ – τ₁ = β, нетрудно найти, что энтропия будет равна нулю. Однако, если смотреть на действие евклидово-шварцшильдовского решения с четырехмерной точки зрения, а не с точки зрения 3 + 1, то нет причин для того, чтобы учитывать поверхностное слагаемое на горизонте, так как там метрика регулярна. Отбрасывая поверхностное слагаемое на горизонте, получаем, что действие равно одной четверти площади горизонта, что как раз равно внутренней гравитационной энтропии черной дыры.

Тот факт, что энтропия черной дыры связана с топологическим инвариантом (эйлеровой характеристикой), является сильным аргументом в пользу того, что она останется, даже если мы перейдем к более фундаментальной теории. Эта идея предается анафеме большинством физиков, занимающихся частицами, которые представляют очень консервативную публику и хотят, чтобы все было похоже на теорию Янга-Миллса. Они соглашаются с тем, что излучение от черных дыр является тепловым и не зависит от того, как черная дыра образовалась, если ее размеры существенно больше планковской длины. Но они утверждают, что когда черная дыра теряет массу и приближается к планковскому размеру, квантовая общая теория относительности становится неприменимой, и все споры заканчиваются. Однако я опишу мысленный эксперимент с черными дырами, в котором информация теряется, хотя кривизна снаружи горизонта все время остается малой.

Уже давно известно, что в сильном электрическом поле может происходить рождение пар положительно и отрицательно заряженных частиц. Один из способов увидеть это следующий. Заметим, что в плоском евклидовом пространстве частица с зарядом q, например, электрон, будет двигаться по окружности в однородном электрическом поле Е. Можно аналитически продолжить это движение от мнимого времени τ к вещественному t. Тогда возникает пара положительно и отрицательно заряженных частиц, ускоренно движущихся друг от друга за счет растаскивания электрическим полем (рис. 3.11).

Рис. 3.11. В евклидовом пространстве электрон в электрическом поле движется по окружности. 

В пространстве Минковского получается пара противоположно заряженных частиц, ускоренно разлетающихся в противоположные стороны 

Процесс рождения пар может быть описан разрезанием двух диаграмм на половины вдоль линий t = 0 или τ = 0. Соединим после разрезания верхнюю половину диаграммы пространства Минковского с нижней половиной диаграммы евклидова пространства (рис. 3.12). Это дает картину, в которой отрицательно и положительно заряженные частицы, по сути, являются одной и той же частицей. Она туннелирует через евклидово пространство, чтобы пройти от одной мировой линии в пространстве Минковского к другой. В первом приближении вероятность рождения пары равна e ^–I, 

где — Евклидово действие.

Рождение пар в сильных электрических полях наблюдается экспериментально, и вероятность рождения согласуется с этими оценками.

Рис. 3.12. Рождение пар может быть описано объединением половины диаграммы в евклидовом пространстве с половиной диаграммы в пространстве Минковского 

Черные дыры могут нести электрический заряд, поэтому можно ожидать, что они также будут рождаться парами. Однако вероятность этого процесса должна быть крохотной по сравнению с рождением электрон-позитронных пар, поскольку отношение массы к заряду в 10²⁰ больше. Это означает, что любое электрическое поля будет нейтрализовано рождением электрон-позитронных пар задолго до того, как вероятность рождения пары черных дыр станет заметной. Однако существуют решения для черных дыр с магнитными зарядами. Такие черные дыры не могут получится в результате гравитационного коллапса, поскольку в природе отсутствуют элементарные частицы с магнитным зарядом. Но можно ожидать, что такие черные дыры будут рождаться парами в сильном магнитном поле. В этом случае конкуренция с рождением обыкновенных частиц отсутствует, поскольку у таких частиц нет магнитного заряда. Таким образом, в достаточно сильном магнитном поле вероятность рождения пары магнитно-заряженных черных дыр может быть значительной.

Рис. 3.13. Пара противоположно заряженных черных дыр ускоряется в противоположных направлениях магнитным полем

Рис. 3.14. Заряженная черная дыра, движущаяся по окружности в евклидовом пространстве 

В 1976 Эрнст нашел решение, которое представляет две магнитно-заряженные черные дыры, ускоренно движущиеся друг от друга в магнитном поле (рис. 3.13). Если совершить аналитическое продолжение в область мнимого времени, можно получить картину, очень похожую на рождение электрон-позитронных пар (рис. 3.14). Черная дыра движется по окружности в искривленном евклидовом пространстве точно так же, как электрон движется по окружности в плоском евклидовом пространстве. В случае черных дыр ситуация сложнее, поскольку координата мнимого времени периодична как относительно горизонта черной дыры, так и относительно центра окружности, по которой дыра движется. При этом отношение массы к заряду можно подобрать так, чтобы эти периоды стали одинаковыми. Физически это означает, что можно выбрать параметры черной дыры так, что температура черной дыры станет равной температуре, которую она приобретает за счет собственного ускорения. Температура магнитно заряженной черной дыры стремится к нулю по мере того, как заряд стремится к значению массы, выраженной в планковских единицах. Таким образом, для слабых магнитных полей и, следовательно, малых ускорений эти периоды всегда можно подобрать равными друг другу.

Рис. 3.15. Туннелирование приводит к появлению пары черных дыр, что может быть также описано половиной евклидовой диаграммы и половиной лоренцевской диаграммы 

Как и в случае рождения электрон-позитронной пары, рождение пары черных дыр можно описать, соединяя вместе нижнюю половину евклидового решения во мнимом времени с верхней половиной лоренцевского решения в реальном времени (рис. 3.15). Можно считать, что черная дыра туннелирует сквозь евклидову область и выходит оттуда как пара противоположно заряженных черных дыр, которые ускоряются в противоположные стороны под действием магнитного поля. Решение для ускоренных черных дыр не является асимптотически плоским, поскольку оно соответствует наличию однородного магнитного поля на бесконечности. Но, несмотря на это, можно сделать некоторые предположения относительно вероятности рождения пар черных дыр в локальной области магнитного поля. Можно считать, что после их рождения черные дыры попадают в области, где магнитное поле отсутствует. Тогда каждую черную дыру можно рассматривать отдельно как черную дыру в асимптотически плоском пространстве-времени. При этом в каждую дыру можно забросить произвольно большое количество материи и информации. После этого дыры начнут излучать и терять массу. Однако при этом они не могут потерять магнитный заряд из-за отсутствия частиц с магнитными зарядами. В конце концов они вернутся в исходное состояние с массой чуть больше, чем заряд. После этого можно свести обе дыры вместе и позволить им аннигилировать. Процесс аннигиляции может восприниматься как обращение во времени процесса рождения пар. Поэтому он будет представляться верхней половиной евклидова решения, соединенного с нижней половиной лоренцевского решения. В промежутке между рождением пары и ее аннигиляцией имеется длительный лоренцевский период, в течение которого черные дыры удаляются друг от друга, поглощают материю, излучают и потом возвращаются обратно. Топология гравитационного поля будет в этом случае топологией решения Евклида-Эрнста. Это не что иное как S² x S² с одной выколотой точкой (рис. 3.16).

Рис. 3.16. Пара черных дыр, рождающихся за счет туннелирования, в конечном счете аннигилирует вновь за счет туннелирования 

Может вызвать беспокойство то, что при аннигиляции черных дыр будет нарушаться обобщенный закон термодинамики, поскольку в этом случае происходит исчезновение площади горизонта черных дыр. Однако оказывается, что площадь горизонта ускорения в решении Эрнста получается из области, которую бы мы имели, если бы там не было рождения пары. Конечно, это довольно тонкое вычисление, поскольку площадь горизонта ускорения в обоих случаях бесконечна. Тем не менее, существует хорошо определенная ситуация, при которой их разность конечна и равна площади горизонта черной дыры плюс разность в действии для этих решений с учетом и без учета рождения пар. Рождение пары можно понимать, так сказать, как процесс с нулевой энергией, при котором гамильтониан с учетом рождения пары будет совпадает с гамильтонианом без рождения пар. Я благодарен Саймону Россу и Гарри Горовитцу за вычисление этой редукции прямо в течение лекции. Чудеса подобные этому — я подразумеваю результат, а не то, что они его получили — заставляют меня считать, что термодинамика черных дыр не может быть просто низкоэнергетическим приближением. Я глубоко убежден, что гравитационная энтропия не исчезнет, даже если мы перейдем к более фундаментальной теории квантовой гравитации.

Из этого мысленного эксперимента можно видеть, что он приводит к внутренней гравитационной энтропии и потере информации в случае, когда топология пространства-времени отличается от топологии плоского пространства Минковского. Если размер черной дыры, полученной в результате рождения пары, значительно превышает планковский размер, то кривизна повсюду вне горизонтов будет мала по сравнению с планковским масштабом. Это означает, что приближение, которое я делал, отбрасывая кубические и более высокие поправки, является достаточно хорошим. Тогда заключение о том, что в черных дырах теряется информация, является вполне приемлемым.

Если информация теряется в макроскопических черных дырах, она должна также теряться в процессах, где благодаря квантовым флуктуациям метрики проявляются микроскопические, виртуальные черные дыры. Можно считать, что частицы и информация будут попадать в такие черные дыры и при этом теряться. Возможно, только там и происходят такие странные столкновения. Величины, подобные энергии и электрическому заряду, которые связаны с калибровочными полями, будут сохраняться, но вся другая информация и глобальные заряды будут теряться. Все это имеет далеко идущие следствия для квантовой теории.

Обычно предполагается, что система в чисто квантовом состоянии эволюционирует унитарным образом через последовательность чистых квантовых состояний. Но если существует потеря информации за счет появления и исчезновения черных дыр, унитарная эволюция невозможна. Вместо этого, из-за потери информации конечное состояние после исчезновения черной дыры будет так называемым смешанным квантовым состоянием. Его можно рассматривать как ансамбль различных чистых квантовых состояний, каждое со своей собственной вероятностью. Но поскольку система не находится с определенностью в каком-то одном состоянии, нельзя добиться того, чтобы вероятность конечного состояния стала нулевой за счет интерференции с любым квантовым состоянием. Это означает, что гравитация приводит к новому уровню непредсказуемости в физике сверх той неопределенности, которая обычно связывается с квантовой теорией. В следующей лекции (глава 5) я покажу, что мы, возможно, уже наблюдаем эту дополнительную неопределенность. Это означает конец надежде на научный детерминизм, т.е. на способность предсказывать будущее с определенностью. Похоже, что у Бога еще есть в рукаве пара трюков.