Введение в акустику.
Природа звука и ультразвука

Олег Акимов

Предмет, который будет интересовать нас в дальнейшем, относится к акустике — науке, изучающей механические колебания в газах, жидкостях и твердых телах. Исследователей-механиков, занятых этой наукой, именуют акустиками. Акустические волны (их часто называют просто звуком) представляют собой регулярно чередующиеся области сжатия и разряжения какой-либо среды — воздуха, воды, стекла и т.д. Но механическое движение в среде не обязательно должно быть периодическим; оно может быть хаотическим. В этом случае звук называют шумом. Шум почти всегда считается вредным явлением. В отличие от него периодический или даже гармонический звук относится к так называемому полезному сигналу.

Акустика — разветвленная наука, включающая в себя аэроакустику, гидроакустику, акустику в твердых телах (это разделение по фазовому состоянию среды), а также линейную и нелинейную акустику (деление с точки зрения математических уравнений), атомную акустику, гидролокацию и т.д. Существует междисциплинарная наука, цель которой — борьба с различными, главным образом, промышленными шумами. Наиважнейшей задачей акустиков, работающих с шумами, является повышение отношения уровня полезного сигнала к уровню шума или, говорят, белого шума, если речь идет об абсолютно случайном шуме, а не о работе какого-нибудь монотонно шумящего двигателя. Далее мы займемся изучением главным образом характеристик звука.

Акустические колебания улавливаются ушами (у человека и животных) или заменяющими их слуховыми органами (у рыб, земноводных и насекомых ушей, как таковых, нет, но слышат они прекрасно). В табл. 1 приведены диапазоны слышимости для некоторых биологических видов, а также частота музыкальных нот первой октавы. Частота колебаний второй октавы получается удвоением частоты первой октавы. Например, частота колебаний ноты ля второй октавы равна 880 Гц, ля третьей октавы — 1720 Гц, а ля малой октавы — 220 Гц и т.д.

Таблица 1
Диапазон слышимости и частота
звучания нот первой октавы

Человек Собака Кошка Кузнечик Землеройка Летучая мышь Дельфин

20 Гц — 20 кГц 15 Гц — 50 кГц 60 Гц — 60 кГц 5 кГц — 95 кГц 7 кГц — 115 кГц 7 кГц — 200 кГц 4 кГц — 200 кГц

До Ре Ми Фа Соль Ля Си

261,63 Гц 293,66 Гц 329,63 Гц 349,23 Гц 392,00 Гц 440,00 Гц 493,88 Гц

Добавим к сказанному, голосовые связки человека при разговоре издают звуки с частотой от 300 до 3000 Гц. Талантливые певцы способны перекрывать несколько музыкальных октав. Относительно человеческого слуха следует также добавить, что у слепых он более развит и может лежать в пределах от 15 Гц до 23 кГц. Кроме того, некоторые из них чувствуют звук костями черепа, который играет роль резонатора. В этом случае верхняя граница простирается до 200 кГц. Слепые, как правило, хорошо слышат ногами, например, шаги, которые отдаются по полу. Частоты ниже 50 Гц могут ощущаться кожей. Частоты выше 10 кГц быстро затухают, поэтому писк комара можно услышать только вблизи уха.

Почему, когда заводят речь об акустике, в первую очередь приводят пределы слышимости и музыкальный ряд (см. табл. 1)? Дело в том, что сам термин akustik связан с древнегреческими словами: слушать, слышимый, слуховой и т.д. Исторически сложилось так, что развитие этой древней отрасли знаний, осуществленное пифагорейцами в 6-3 веке до нашей эры, происходило при разработке музыкальной теории и конструировании музыкальных инструментов. В 17 веке нашей эры эта наука стала частью физики, рассматривающей механические колебания.

Знаменитый французский ученый Жан Батист Жозеф Фурье (1768 — 1830) доказал, что любой сколь угодно сложный периодический процесс можно представить в виде некоторой совокупности гармонических колебаний. Эта его теорема широко используется в современных приборах, предназначенных для спектрального анализа. На ее основе можно понять, почему ухо способно различить отдельные звуки, одновременно издаваемые, например, движущимся поездом, громкоговорителем, установленным на железнодорожной станции, и голосом собеседника, который вызвался вас провожать.

Они не перемешиваются потому, что в ушной улитке могут возникать сразу несколько стоячих волн, которые образуются, например, в воздушном столбе трубы и органа или на струнах гитары и скрипки. В идеальном случае стоячая волна существует сколь угодно долго. Но из-за потерь акустической энергии в резонаторах, звук постепенно угасает. Для его поддержания требуется непрерывная подпитка дополнительной энергией, которая доставляется в нужные точки резонатора с помощью бегущей волны. Бегущие и стоячие волны сосуществуют вместе, образуя динамичный рисунок, наблюдающийся на колеблющейся струне.

Ультразвуком называют звуковые колебания, частота которых превышает верхний порог слышимости человека, причем частота 20 кГц является нижней границей ультразвукового диапазона. Верхней границей для него служит частота порядка одного миллиарда колебаний в секунду, т.е. 10 ⁹ Гц = 1 ГГц (говорят, один гигагерц). Частота колебаний свыше 1 ГГц называется гиперзвуком, а ниже диапазона слышимости человека, т.е. менее 20 Гц — инфразвуком (эти частоты нас интересовать не будут).

Важнейшим параметром любых акустических волн — звука, ультразвука или гиперзвука — является скорость распространения их в среде. Без среды никакие волны существовать не могут. Именно физические свойства среды — ее плотность ( ρ ) и сжимаемость ( β ) — определяют скорость звука в общем виде:

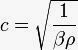
Для газов эту формулу можно несколько детализировать:

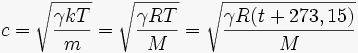
где γ — показатель адиабаты: 5/3 для одноатомных газов, 7/5 для двухатомных (и для воздуха), 4/3 для многоатомных; k — постоянная Больцмана; R — универсальная газовая постоянная; T — абсолютная температура в кельвинах; t — температура в градусах Цельсия; m — молекулярная масса; M — молярная масса.

По порядку величины скорость звука в газах близка к средней скорости теплового движения молекул и в приближении постоянства показателя адиабаты пропорциональна квадратному корню из абсолютной температуры.

Для твёрдых тел скорость звука вычислисляется по другой формуле:

,

где K — модуль всестороннего сжатия; E — модуль Юнга; ν — коэффициент Пуассона.

Приведенные формулы работают до тех пор, пока длина акустической волны ( λ ) огромна по сравнению с межмолекулярными расстояниями и размерами самих молекул. Но как только эти условия перестают выполняться, наблюдается дисперсия (от лат. dispergo — рассеивать), т.е. рассеяния звуковой энергии на молекулах вещества, что всегда приводит к падению скорости распространения колебательного возбуждения.

В табл. 2 приведена зависимость длины волны от частоты в трех упругих средах без затухания. В указанном диапазоне частот скорость звука, как произведение длины волны на частоту ( c = λ · f ), в воздухе, воде и дереве остается неизменной — 5000, 1450 и 340 м/с, соответственно. Еще раз подчеркнем, что эти скорости всецело определяются плотностью (ρ) и упругостью (μ) среды; длина волны (λ) и частота колебаний (f ) не определяют скорости звука. Между тем, бытует мнение, будто два последних параметра являются причинами появления того или иного значения c.

Таблица 2
Длина акустических волн в трех средах
без дисперсии в зависимости от частоты.

f , частота колебаний 20 Гц 50 Гц 100 Гц 200 Гц 1 кГц 5 кГц 10 кГц 20 кГц 50 кГц 100 кГц 200 кГц 500 кГц 1 МГц

λ в дереве c = 5000 м/с 250 100 50 25 5 1 0,5 0,25 0,1 0,05 0,025 0,01 0,005

λ в воде c = 1450 м/с 72,5 29 14,5 7,25 1,45 0,29 0,145 0,073 0,029 0,015 0,007 0,003 0,0015

λ в воздухе c = 340 м/с 17 6,8 3,4 1,7 0,34 0,068 0,034 0,017 0,0068 0,0034 0,0017 0,0007 0,0003

Даже при частоте миллион колебаний в секунду длина волны остается вполне видимой величиной для невооруженного глаза: 5 мм для дерева, 1,5 мм для воды и 0,3 мм для воздуха, что намного больше геометрических размеров молекул или межмолекулярных расстояний в твердых телах, жидкостях и газах.

Так, средний диаметр молекул газа составляет 6 · 10 ^–10 м, расстояние между молекулами газа — 3 · 10 ^–9 м, размеры полимерных молекул, например, липопротеидов — (3 ÷ 5) · 10 ^–8 м, диаметр эритроцита — 8 · 10 ^–6 м, диаметр капилляра — (4 ÷ 10) · 10 ^–6 м, диаметр артерии — 10 ^–2 м.

Упругие вещества вроде дерева, воды и воздуха с указанной в табл. 2 длиной волны ведут себя как сплошные среды, в которых не различаются отдельные частички. Поэтому такие, казалось бы, очень быстрые колебательные возбуждения, распространяются абсолютно беспрепятственно внутри них, т.е. без потерь энергии, которая в ином случае рассеивалась бы на молекулах в виде тепла.

В первую очередь скорость звука зависит от фазового состояния — будет ли вещество находиться в парообразном (газовом) состоянии, жидком или твердом. Так, например, скорость звука в пресной воде равна 1482 м/с или 5335 км/ч. В водяном паре она существенно меньше — 405 м/с. Лёд же проводит акустические волны со скоростью почти в 10 раз быстрее — 3980 м/с. В солёном растворе, когда плотность жидкости заметно повышается, увеличивается и скорость звука. Так, в морской воде скорость звука больше, чем в пресной, и равна 1533 м/с, а в насыщенном растворе поваренной соли (NaCl) она составляет 1650 м/с.

В демонстрационной табл. 3 приведены скорости распространения акустических колебаний для различных сред. Из неё видно, что в среднем скорость звука для жидких сред выше, чем для газовых, но ниже, чем для твердых. Однако для водородного газа эта скорость намного больше, чем для жидкого эфира, бензина, ацетона и спиртов. Аналогичное нарушение закономерности наблюдается и для твердых веществ. Твердый свинец проводит звук чуть медленнее, чем бензол, а керосин и глицерин быстрее, чем резина и графит.

Таблица 3
Скорость звука в некоторых средах

Газовые среды Пары эфира Хлор Пары спирта Углекислый газ Кислород Ацетилен Воздух (0 °C) Воздух (20 °C) Азот Угарный газ Водяной пар Аммиак Метан Неон Гелий Водород Жидкие среды Кислород жидкий Эфир Спирт (метил.) Бензин Спирт (этил.) Ацетон Толуол Бензол Ртуть Вода пресная Вода морская Раствор NaCl Свинец распл. Глицерин Олово распл. Керосин Твердые среды Свинец Стеарин Графит Резина Эбонит Золото Медь Кирпич Чугун Лед Сосна Железо Стекло Сталь Алмаз

м/с 179 206 230 259 316 327 331 343 334 338 405 415 430 435 965 1284 м/с 912 985 1143 1170 1180 1190 1324 1324 1453 1482 1533 1650 1790 1923 2270 2330 м/с 1322 1380 1470 1600 2400 3240 3560 3600 3850 3980 5030 5130 5640 6000 18000

Легкость и высокая подвижность газовых молекул (как, например, у водорода и гелия) способствует скорейшему распространению колебаний. Чем выше температура газовой среды, тем больше ее упругость, подвижность отдельных молекул и, следовательно, тем выше скорость распространения звука. Так, воздух при нулевой температуре проводит звуковые колебания со скоростью 331 м/с, а при комнатной температуре — 343 м/с.

Но с падением температуры воздух «густеет», его плотность растет. Рассчитывая в нём скорость звука, нужно учитывать что-то одно — либо температуру, либо плотность. Обычно говорят о зависимости скорости звука от температуры, которая увеличивается примерно на 0,6 м/с с повышением температуры на 1°C. Более точная температурная зависимость отображается следующей формулой (здесь t измеряется в °C):

c = 331,5 (1 + t / 273,5) ^½ .

Таблица 4
Изменения скорости звука в сухом воздухе
от изменений его температуры или плотности;
в последнем столбце указано сопротивление Z

c, м/с 351,96 349,08 346,18 343,26 340,31 337,33 334,33 331,30 328,24 325,16 322,04 318,89 315,72

t, °C +35 +30 +25 +20 +15 +10 +05    0 –5 –10 –15 –20 –25

ρ, кг/м³ 1,1455 1,1644 1,1839 1,2041 1,2250 1,2466 1,2690 1,2920 1,3163 1,3413 1,3673 1,3943 1,4224

Z, H·с/м³ 403,2 406,5 409,4 413,3 416,9 420,5 424,3 428,0 432,1 436,1 440,3 444,6 449,1

.

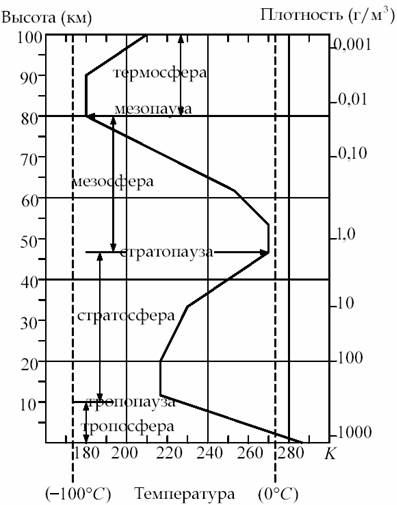
Рис. 1. Вертикальный профиль температур и плотностей воздуха
в атмосфере Земли в течение июня на широте Москвы.

В четвертом столбце табл. 4 приведены значения акустического сопротивления, которое равно произведению плотности среды на скорость звука или, иначе, отношению звукового давления ( p ) к скорости перемещения отдельно взятой частицы ( v ):   Z = ρc = p / v .

Двоякое определение сопротивления позволяет найти колебательную скорость частицы среды:   v = p / cρ , которая всегда намного меньше скорости звука, так как   v / c = p / ρ << 1.   Поскольку плотность и скорость звука — константы, то изменения колебательной скорости частицы всецело зависит от колебаний давления, вызванного акустической волной.

Коэффициент отражения плоских волн при нормальном падении на плоскую границу раздела двух сред определяются отношением их сопротивлений:

K = | Z₁ – Z₂ | / | Z₁ + Z₂ | .

Так, например, если акустическая волна идет из воздушной среды ( Z₁ = 430 H · с / м³ ) в водную ( Z₂ = 1482 · 10³ H · с / м³ ), то вся она, практически, полностью отражается, так как коэффициент отражения близок к единице (K = 0,999). В самом деле, нырнув под воду, мы ничего не слышим, когда нам что-то кричат с берега. Звук кричащего отражается от водной глади и не проходит к нырнувшему. Ничего не изменится, если акустические колебания направить в обратном направлении — из воды в воздух.

Но когда мы имеем дело со средами, близкими по величине сопротивления, как например пара жир-вода (у жира Z = 1335 · 10³ H · с / м³ ), картина радикальным образом меняется, поскольку коэффициент отражения резко падает, в данном случае до K = 0,1. Это обстоятельство приводит к тому, что в человеческом организме, в котором имеется множество областей с близкими значениями сопротивления, локация сильно затруднена.

В частности, для пары жир-мышцы коэффициент отражения тоже равен примерно 0,1; для пары кость-мышцы — 0,65; для пары кровь-почки — 0,03. Но если в почках имеются вредные отложения, то коэффициент отражения от таких почечных камней достигает 0,3, что позволяет легко обнаружить их при помощи приборов, основанных на локационном принципе.

При заданной амплитуде плотность потока энергии зависит от квадрата частоты колебаний. Следовательно, при малых амплитудах можно достичь большой интенсивности, особенно, когда колебания находятся в области высоких частот, в частности, попадают в диапазон ультразвука. Тогда их распространение в среде сопровождается нелинейными эффектами, например, волна синусоидальной формы превращается в пилообразную кривую. Интенсивный ультразвук сильнее поглощается средой, поскольку значительная часть его энергии расходуется на деструкцию среды, если она находится в твердом состоянии. В газах и жидкостях энергия идет на так называемое акустическое течение молекул, скорость которого зависит от коэффициента вязкости среды.

Учитывая глубину проникновения в среду, в воздухе и других газах обычно используется ультразвук низкой частоты, порядка 1,5 · 10 ⁴ ÷ 10 ⁵ Гц, для жидкостей — средней частоты, 10 ⁵ ÷ 10 ⁷ Гц, и для твердых веществ — высокой частоты 10 ⁷ ÷ 10 ⁹ Гц. Частота и длина волны, как мы знаем (см. табл. 2), тесно связаны через скорость распространения. Например, частотному диапазону Δf = 10 ⁷ ÷ 10 ⁹ Гц отвечает диапазон длин волн в воздухе Δλ = 3,4 · (10 ^–3 ÷ 10 ^–5) см, в воде — Δλ = 1,5 · (10 ^–2 ÷ 10 ^–4) см, в стали — Δλ = 5 · (10 ^–2 ÷ 10 ^–4) см.

На границе ультразвука и гиперзвука длина волны в воздухе составляет λ = 3,4 · 10 ^–5 см сопоставима с длиной свободного пробега молекул, что существенно препятствует распространению волн в этой среде. В жидкостях гиперзвук распространяется с трудом. Область его применения — твердые тела, предпочтительно, в монокристаллическом виде. На частоте f = 1,5 · 10 ⁹ Гц с прохождением каждого сантиметра гиперзвук ослабляется в два раза. Такая частота акустических волн сопоставима уже с электромагнитными колебаниями, поэтому все явления, связанные с гиперзвуком, сказываются на электромагнитных явлениях и наоборот.

Возникающие в кристалле высокочастотные колебания образуют оптическую и акустическую составляющую. Оптическая компонента вызвана электромагнитными излучениями и поглощениями при переходе электронов с одного энергетического уровня на другой. При этом часть энергии рассеивается на кристаллической решетке как раз в виде гиперзвука вперемешку с тепловым излучением. Подобно тому, как свет излучается и поглощается порциями, называемыми фотонами, гиперзвук излучается и поглощается фононами — акустическими квантами.

Поскольку ультразвуковые приборы широко используются в медицине, давайте немного задержимся на акустических колебаниях этого диапазона. Прежде всего заметим, что слово ультразвук сокращают до аббревиатуры УЗ. Последнюю букву в аббревиатуре УЗИ расшифровывают по-разному: ультразвуковое излучение, изображение или исследование. Широко принятыми терминами являются: УЗИ-обследование, УЗИ-прибор, и намного реже: УЗ-обследование, УЗ-прибор. В основу физической работы УЗИ-прибора положен эффект Доплера. О нем подробно рассказывается на нашем сайте в следующих разделах:

• О формуле, описывающей эффект Доплера
• Естествознание. Лекция 4. Эффект Доплера
• Классический эффект Доплера: 1 | 2 | 3 | 4 | 5
• Часто задаваемые вопросы по эффекту Доплера
• Идиотский расчет эффекта Доплера
• Использование в медицине поперечного эффекта
  Доплера для ультразвуковой диагностики
  сердечно-сосудистой системы
• Эффект сдвига воспринимаемой длины волны в красную область
• Моделирование волновых процессов. Эффект Доплера

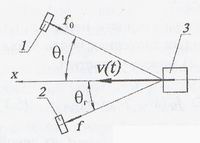
Суть дела заключается в следующем. УЗИ-прибор посылает УЗ колебания, например, в область сердца. Его мышцы периодически сокращаются, что вызывает движение крови во всей сосудистой системе человека. В этой ситуации проявляется эффект Доплера, который описывается так называемой традиционной формулой:

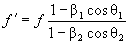
Здесь f — частота излучения УЗИ-прибора и f ' — частота, эхо-излучения, идущего от движущихся эритроцитов крови и принятая приёмником УЗИ-прибора; β₁ = v₁/c — относительная скорость излучателя УЗ, β₂ = v₂/c — относительная скорость приёмника эхо-излучения, c — средняя скорость распространения УЗ в организме человека; углы θ₁ и θ₂ образованы волновым вектором с вектором скорости движения, соответственно, приёмника v₁ и источника v₂.

На эритроцитах происходит отражение УЗ сигнала, поэтому они сначала играют роль движущихся приёмников, затем — движущихся источников УЗ. Это обстоятельство сводит формулу, описывающую эффект Доплера, к виду:

.

Отсюда мы можем определить относительную скорость движения эритроцитов:

β = ( f ' – f ) / 2 f cos θ .

При средней скорости ультразвука в организме человека c = 1540 м/с, скорость движения эритроцитов v лежит в пределах от нескольких сантиметров до 1 – 2 метров в секунду.

Традиционная формула позволяет найти скорость движущихся частиц только в том случае, когда излучатель и приёмник находятся под косыми углами к потоку: θ < 60°; при больших углах θ возникает большая погрешность. Если углы прямые: θ = ±90°, то определение скорости эритроцитов ( β или v ) становится делом совсем не возможным, так как f ' = f.

Между тем, рис. 2. отчетливо демонстрирует нам, что воспринимаемая наблюдателем длина волны λ ', соответствующая воспринимаемой частоте f ', зависит не только от величины угла θ, но и от величины относительной скорости β. Нам говорят, что какой бы ни была скорость β, равенство λ ' = λ всегда наступит при угле θ = ±90°. Так думать — значит, сильно заблуждаться.

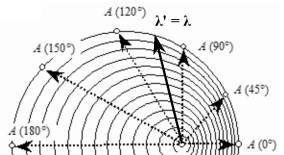
Рис. 2. Картина волн, расходящихся от движущегося вправо источника колебаний. Объективно мы видим, что для точки А (0°) λ ' = λ (1 – β), для точки А (180°) λ ' = λ (1 + β). Вопрос: при каком угле θ можно будет наблюдать равенство λ ' = λ? Может быть, при θ = ±90°? Нет, это ошибка, так как величина угла θ явно зависит от значения β.

Неважно, где находится наблюдатель — рядом с источником, где-то в одной из точек А или смотрит на волновую картину откуда-нибудь сверху — в любом случае он сможет снять зависимость λ ' от угла θ и скорости β:

при θ = 0° ,   λ ' = λ (1 – β) ;       при θ = 180° ,   λ ' = λ (1 + β).

Эти две формулы элементарны и всем известны со школьной скамьи. Трудности вызывал случай равенства длин волн: λ ' = λ. Где, в каком месте представленной здесь картины волн он произойдет?

Традиционно считалось, что этот момент наступит при угле θ = 90°. Но интуитивно каждый понимаем, что значение искомого угла θ зависит от скорости источника колебаний: чем больше скорость β, тем больше линия, где λ ' = λ, отклоняется влево от вертикали (рис. 2), т.е. угол θ становится всё более тупым. Не может получаться так, что скорость β как-то меняется, а угол θ остается постоянно прямым.

Итак, из ранее приводимой формулы:

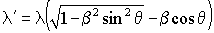
нам нужно определить, как меняется угол θ в зависимости от скорости β, когда выполняется равенство : λ ' = λ. Если подставить это условие в данную формулу, то найдем простую зависимость :

β   =   – 2 cos θ     или     θ   =   arccos ( – β / 2 ) .

Для наглядности составим нижеследующую таблицу, из которой можно видеть, что любая скорость источника приводит к отклонению луча, для которого λ ' = λ, от вертикальной линии в противоположную сторону от направления движения источника. Данное отклонение является следствием проявления аберрации, хорошо известное физикам. Если β > 0, то θ > 90°. По достижении скорости β = 1, угол отклонения в точности равен θ = 120°.

Таблица 5
Скорости β и углы θ, сохраняющие
условие равенства длин волн λ ' = λ.

β 0,0001 0,001 0,01 0,1 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2

θ 90°,003 90°,03 90°,3 92°,9 95°,7 101°,5 107°,5 113°,6 120°,0 126°,9 134°,4 143°,1 154°,1 180°,0   —

Ничего качественно нового не произойдет, когда скорость звука будет преодолена (рис. 3): β > 1. И только при β ≥ 2 наступает ограничение для выполнения условия λ ' = λ. Скорость источника может быть, конечно, любой, в том числе и β = 2,2 , только воспринимаемая длина волны никогда не будет равна собственной длины волны источника: λ ' ≠ λ.

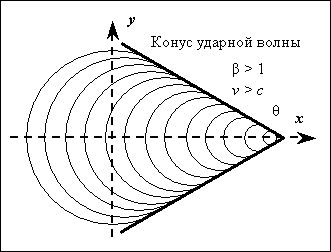
Рис. 3. Конус ударной волны образуется при β > 1.

Что здесь может помешать выполнению условия λ ' = λ ? Разве кто-нибудь отменял выше написанные формулы —

при θ = 0° ,   λ ' = λ (1 – β) ;         при θ = 180° ,   λ ' = λ (1 + β) ?

Да, первая формула для угла θ = 0° здесь отменена. Дело в том, что исходная формула накладывает еще одно ограничение на углы и скорости, а именно: подкоренное выражение всегда должно быть положительным:

1 – β² sin ² θ ≥ 0,     sin θ   ≤   ±1 / β   или   θ   ≤   ± arcsin ( 1 / β ).

Это ограничение дает формулу Маха для нахождения углов внутри конуса ударной волны. Пусть β = 2,2 , тогда, согласно последнему ограничению, имеем:

θ   ≤   ± arcsin ( 0,45 )   =   ± 27°.

Это означает, что при β = 2,2 волны не выходят за пределы конуса ударной волны с углами при вершине ±153°, если отсчет вести от положительного направления оси x. Таким образом, при θ = 180° будем иметь λ ' = 3,2 λ, что допустимо, а угол θ = 0° в этой ситуации мы просто не имеем права рассматривать. В этом направлении у нас получилась бы отрицательная длина волны λ ' = –1,2 λ, что с точки зрения физики лишено всякого смысла. Эта важная тема более детально обсуждается на странице

Использование в медицине поперечного эффекта
Доплера для ультразвуковой диагностики
сердечно-сосудистой системы

До сих пор была рассмотрена ситуация с одним движущимся источником. Когда же движутся и источник и приемник, исходная формула изменится на следующую:

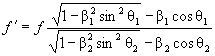
В этом случае для нахождения β или v, когда θ < 60°, можно будет воспользоваться выражением —

β = ± ( sin² θ + F ² cos² θ ) ^{– ½} ,   где   F = ( f ' + f ) / ( f ' – f ) ,

а когда θ = ± 90°, точным выражением —

β = ±[ 1 – (f ' / f )² ] ^{– ½} .

Насколько заметно отличаются результаты вычислений по формуле Доплера для плоской и сферической волны, если иметь в виду медицину? Остановимся на этом важном для нас моменте и рассмотрим его чуть более детально. Обычно рассуждают следующим образом.

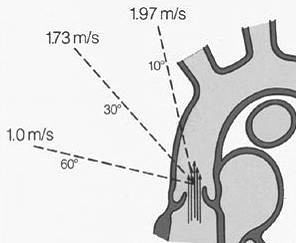
Пускай через клапан аорты сердечной мышцей кровь выталкивается со скоростью v = 2 м/с. Если смотреть на вектор скорости под углом θ = 0°, то cos θ = 1 и воспринимаемая датчиком скорость таковой и будет: v ' = v = 2 м/с. Если смотреть на вектор под углом θ = 90°, то cos θ = 0 и воспринимаемая датчиком скорость v ' = 0 м/с. Если взять три значения угла, например, θ = 10°, 30° и 60°, то воспринимаемые датчиком скорость v ' = v cos θ будет соответственно равна v ' = 1.97 , 1.73 и 1.0 м/с (рис. 4). Поскольку локация эритроцитов производится при помощи ультразвука, распространяющегося со скоростью с = 1540 м/с, то воспринимаемая датчиком скорость будет не v ', а

с ' = с – v cos θ,

которая и определяет закон Доплера в его традиционном понимании.

Рис. 4. Если скорость кровотока, идущего через клапан аорты составляет v = 2 м/с, то измерение ее под углами θ = 10 °, 30 ° и 60 ° даст величины v ' = 1.97, 1.73 и 1.00 м/с, соответственно.

Эти рассуждения кажутся настолько безупречными, что никто и никогда их не ставил под сомненье. Между тем, с точки зрения физических процессов, протекающих в приборах, основанных на принципе локации, такая логика справедлива только для плоских волн. Если же источник излучения точечный и волны расходятся сферически, то воспринимаемая датчиком скорость кровотока изменится на известное нам выражение:

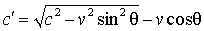
Очевидно, что разница величин между плоским и сферическим случаем всецело определяется радикалом, который показывает, насколько 1 отличается от квадратного корня:

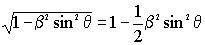
При локации, как мы знаем, эффект Доплера удваивается (2β cos θ) за счет падающего ( П_i ) и отраженного ( О_i ) луча (рис. 5), поэтому искомая сферическая поправка определяется выражением β² sin² θ.

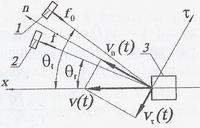
а)

б)

в)

Рис. 5. Схема ультразвуковой локации движущегося одиночного объекта: а — с разнесенными приемником и передатчиком; б — с близко расположенными друг к другу приемником и передатчиком (1 — передатчик, 2 — приемник, 3 — объект локации, v ( t ) — скорость объекта); в — падающие ( П_i ) и отраженные ( О_i ) волны; угол падения равен углу отражения, следовательно, вернувшийся в прибор отраженный луч испытает эффект Доплера дважды.

При типичных для биомедицины скоростях порядка β = 0,001 будем иметь значения, которые занесены в табл. 6.

Таблица 6
Эффект Доплера и сферические поправки к нему
для биомедицинской скорости β = 0,001

θ 0° 10° 20° 30° 45° 60° 70° 75° 80° 85°	2β cos θ · 10–3 2.000 1.970 1.879 1.732 1.414 1.000 0.684 0.518 0.347 0.174	β²sin² θ · 10–6 0.00 0.03 0.12 0.25 0.50 0.75 0.88 0.93 0.97 0.99
86° 87° 88° 89° 89,2° 89,4° 89,6° 89,8° 89,9° 90,0°	0.139 0.105 0.070 0.035 0.028 0.021 0.014 0.007 0.003 0.000	0.995134 0.997261 0.998782 0.999695 0.999805 0.999890 0.999951 0.999988 0.999997 1.000000

Таким образом, при частоте излучателя f = 10 МГц прибор, работающий по сферической формуле, зарегистрирует поперечный эффекта Доплера, равный 10 Гц. При углах 60° и 120° ошибка составит 7,5 Гц и т.д.

Так как сферическая поправка пропорциональна β², а величина Доплер-эффекта — β, то разница между результатами измерения по формуле для плоской волны и сферической в широком диапазоне углов крайне незначительная. Однако при углах θ = 90° ± 5° вклад поправки β²sin² θ возрастает. Чтобы исключить провал достоверных данных по скорости кровотока в этом узком секторе углов, необходимо воспользоваться доплеровской формулой именно для сферической волны. На Западе вот уже несколько лет выпускаются медицинские УЗИ-аппараты, способные определять скорость эритроцитов и на прямых углах θ, равных 90°.

В справедливости действия сферического закона Доплера можно убедиться на примере сравнительно доступной и безопасной стрельбы из пневматического ружья (рис. 6). В воздухе скорость звука в 4,5 меньше, чем в органической среде; примем ее равной c = 330 м/с. Пусть скорость пули в месте, где измеряется доплеровская частота, равна v = 110 м/с; в этом случае β = 1/3. Приблизительно при угле θ = 81.6° (табл. 7) величина сферической поправки становится равной величине эффекта Доплера:

2β cos θ = β²sin² θ = 0.088 .

Таблица 7
Эффект Доплера и сферические поправки к нему
для движущейся пули пневматического ружья β = 1/3

θ 0° 10° 20° 30° 45° 60° 70° 75° 80° 81.6 85°	2β cos θ 0.60 0.59 0.56 0.52 0.42 0.30 0.21 0.16 0.10 0.088 0.052	β²sin² θ 0.000 0.003 0.011 0.023 0.045 0.068 0.079 0.084 0.087 0.088 0.089
86° 87° 88° 89° 89,2° 89,4° 89,6° 89,8° 89,9° 90,0°	0.042 0.031 0.021 0.010 0.008 0.006 0.004 0.002 0.001 0.000	0.089562 0.089753 0.089890 0.089973 0.089982 0.089990 0.089996 0.0899989 0.0899997 0.0900000

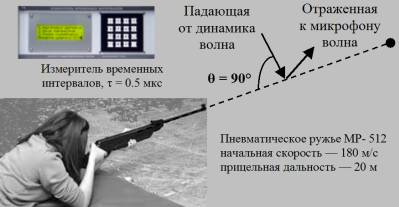
Рис. 6. Эксперимент по измерению поперечного Доплер-эффекта

Этот эксперимент несложно осуществить. «Школьное» пневматическое ружье МР-512 может использоваться для охоты на змей и мышей. У него начальная скорость вылета пули равна v = 180 м/с. На расстоянии d = 20 м пуля обладает скоростью порядка 110 м/с и способна убить даже крысу. Есть пневматические оружья, стреляющие пулями с начальной скоростью, равной скорости звука, т.е. порядка v = c = 330 м/с. Ружье считается хорошим, если оно стреляет с начальной скоростью v = 250 м/с и поражает цель на расстоянии d = 50 м с убойной скоростью пули 150 м/с.

Для проведения эксперимента по измерению поперечного Доплер-эффекта лучше взять, конечно, профессиональное оружье типа Diana 52 (v = 320 м/с, d = 75 м) или Gamo Hunter 440 (v = 305 м/с, d = 60 м). Стрелять нужно в тире, в котором на расстоянии 50 м установлены звуковой генератор вместе с динамиком и приемник с микрофоном и усилителем.

Приемник должен быть избирательным, т.е. иметь высокодобротный резонансный контур, заранее настроенный на ожидаемую доплеровскую частоту — в противном случае, отраженная волна будет подавлена падающей. Для точного измерения скорости звука и пули необходим также измеритель временных интервалов, например «Ива-2» с погрешностью τ = 0,5 мкс, и чувствительные фотодатчики к нему. Зная временной интервал и пройденный отрезок пути, всегда можно вычислить скорость.

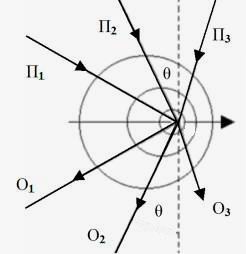
Величина относительной скорости β = 1/3 всё ещё слишком мала, чтобы наглядно увидеть отличие формул для плоского и сферического случая. На рис. 7 взято значение β = 2/3 и в полярных координатах при λ = 1 построены два графика: синяя кривая — она называется кардиоида — для плоского случая и красный круг, лежащий внутри кардиоиды — для сферического случая. Полярные координаты, вычерченные пунктирными линиями, имеют удобную разметку: четыре концентрических окружности радиусами 0.5, 1, 1.5 и 2 масштабных единиц, а также 12 радиальных прямых, отвечающих углам θ = 0°, 30°, 60°, …

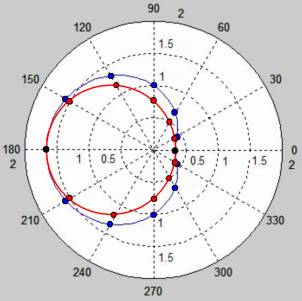
Рис. 7. Графики для β = 2/3 и λ = 1, вычерченные в полярных координатах, как наиболее подходящих;
уравнение окружности: λ' = λ[(1 – β² sin² θ)^½ – β cos θ],
уравнение кардиоиды: λ' = λ(1 – β cos θ);

θ = 0° θ = 30° θ = 60° θ = 90° θ = 120° θ = 150° θ = 180°

λ' = 0.3333 λ' = 0.4226 λ' = 0.6667 λ' = 1.0000 λ' = 1.3333 λ' = 1.5774 λ' = 1.6667

λ' = 0.3333 λ' = 0.3655 λ' = 0.4832 λ' = 0.7454 λ' = 1.1498 λ' = 1.5202 λ' = 1.6667

Часто спрашивают: почему берутся полярные, а не декартовы координаты? Ответ очень прост: полярные координаты больше всего подходят для расходящихся по всем направлениям волн. Теперь отойдем от темы эффекта Доплера и зададимся вопросом: что дает медикам точные знания скорости движения эритроцитов по кровеносной системе человека?

Из физики известно, что сужение просвета в сосуде приводит к увеличению скорости потока. Следовательно, в сосуде, в котором образовалась бляшки, кровь будет течь быстрее, чем в других частях этого сосуда. Данное требование вытекает из закона сохранения массы: жидкая масса (вода, кровь, лимфа), вытекающая из системы трубок, должна быть в точности равна массе втекающей жидкости.

В самом деле, в жесткой трубке с различной площадью сечения в любой момент времени расход жидкости ( Q ) постоянен, что выражается равенством произведения скорости ( u_i ) на соответствующую площадь сечения ( A_i ):

Q = u₁ A₁ = u₂ A₂.

В предельно эластичной трубке площадь сечения может меняться под действием внутреннего давления. Тогда за счет разности в расходе жидкости ΔQ произойдет увеличение объема в заштрихованной области (рис. 8):

ΔQ = Q₁ – Q₂ = u₁ A₁ – u₂ A₂.





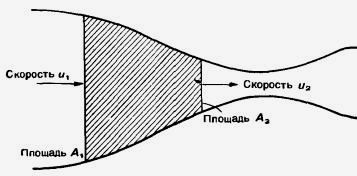
Рис. 8. Трубка с переменным сечением (взято из [1, с. 60] ).

Здоровые кровеносные сосуды обладают кратковременной эластичностью, но при длительном патологическом сужении отверстия трубки действует закон сохранения жидкой массы.

Таким образом, УЗИ-прибор позволяет найти места нарушения кровоснабжения органа или ткани по причине закупорки сосуда какими-либо частицами. Ультразвуковая диагностика позволяет обнаруживать тромбозы, эмболию, спазмы сосудов, врожденные пороки сердца, возрастные дефекты клапанов сердца и ног, закупорку кровеносных сосудов, области с неудовлетворительной циркуляцией крови вокруг головного мозга и многое другое. Ультразвуковая локация способена отличить ламинарный кровоток от турбулентного, когда в кровотоке образуются завихрения. Последние возникают по причине какого-нибудь дефекта сердечно-сосудистой системы, препятствующего протеканию крови.

Далее мы продолжим вводить важнейшие понятия, характеризующие параметры некоего идеального колебательного процесса, взятые преимущественно из "Физической энциклопедии" [2]. В упругой среде без дисперсии плоская волна описывается гармоническим законом, амплитуда которого не затухает с течением времени и может передаваться в неизменном виде на бесконечно большие расстояния:

p = P cos ( ωt – kx + φ ),

где p — звуковое давление, P — амплитуда или максимальное значение p, ω = 2πf — круговая частота колебаний, k = 2π / λ — волновое число, φ — начальная фаза колебаний, x — ось абсцисс, вдоль которой упругая волна распространяется со скоростью c = ω / k в течение времени t. Заметим попутно, что понятия волнового числа удобно совмещать с понятием круговой (угловой или циклической) частоты, которая измеряется в радианах за секунду [рад/с].

В единицах СИ давление измеряется в паскалях: 1 Па = 1 Н · м²; в системе СГС используется 1 дин / см² = 0,1 Па = 0,1 Н / м². Внесистемными единицами являются техническая атмосфера: 1 ат = 0,98 · 10 ⁶ дин / см² = 0,98 · 10 ⁵ Н / м² и бар: 1 бар = 10 ⁶ дин / см².

Волновое число — это длина волнового вектора, направление которого совпадает с направлением распространения волны. Таким образом, волновой вектор перпендикулярен к линии или поверхности волнового фронта и совпадает с направлением импульса, который действует на каждую частичку среды. В частности, в квантовой механике хорошо известна элементарная формула p = ħk, где ħ — постоянная Планка. В классической механике ей ставится в соответствие выражение p = Ek / ω, где E — акустическая плотность энергии. В анизотропных средах, к которым относится большинство кристаллов, направление импульса или волнового вектора может не совпадать с направлением переноса акустической энергии.

В идеальном случае недисперсионной среды смещение (a) частицы под воздействием давления p можно определить через колебательную скорость частицы v и другие известные нам параметры следующим образом:

a = v / 2π f = p / 2π f Z = p / Z ω = v / ω .

Колебательная скорость ( v ) отличается как от скорости распространения звуковой волны ( c ), так и от скорости перемещения самой среды. Давление, создаваемое акустической волной, пропорционально произведению круговой частоты (ω), плотности среды (ρ), скорости звука ( c ) и смещению ( a ). Для гармонического колебания среды с максимальным смещением частиц от положения равновесия ( A — амплитуда колебаний) имеем следующие выражения для давления:

p = ωρca = ωZa = Zu / ω = c ( ρE ) ^½ = ( NE / A ) ^½

где   u — ускорение частицы как первая производная от скорости ( v ) или вторая производная от смещения ( a ),   N — мощность звука [Вт],   E — акустическая плотность энергии [ Вт · с / м³ ].

Максимальное давление в среде ( P ), отвечающее амплитуде A, создается на расстоянии λ/4; на расстоянии λ/2 давление равно первоначальному (равновесному); на расстоянии 3λ/4 давление снова становится максимальным, но действует уже в противоположном направлении, так как частицы среды отклоняются в обратную сторону. Максимального ускорения ( U = 2ωA ) движущиеся частицы достигают на расстоянии λ/2 при первоначальном давлении среды.

Интенсивность звука ( I ) выражается отношением потока звуковой энергии к площади поверхности, которую этот поток пересекает — E / S  [Вт/м²] . Для плоской акустической волны, падающей на поверхность перпендикулярно, интенсивность можно выразить через давление, колебательную скорость и сопротивление:

I = pv / 2 = Zv² / 2 = p² / 2Z

Локальное давление среды создается смещением самостоятельных частиц или бесконечно малых объемов непрерывной среды, колеблющихся около положения равновесия (например, исходное атмосферное давление) при прохождении звуковой волны. Локальное отклонение давления от давления равновесного, как правило, очень мало. Например, оглушительный звук при взлете реактивного самолета создает в атмосфере Земли на уровне океана перепады давления порядка 101323,6 — 101326,4 Па.

Перепады давления измеряются беллах (Белл — изобретатель телефона): 1 белл = log (P / P_о). На пракимке удобно пользоваться десятичными логарифмами:

1 дБ   =   10 lg ( p² / p²_о )   =   20 lg ( A / A_о ) ,

где   p   ( или   А ) — давление (или амплитуда) звукового сигнала, которая сравнивается с некоторым базовым давлением   p_о   (или базовой амплитудой   A_о ). В качестве базовой величины берется давление 20 микропаскаль   ( 20 μПа ).

Если мощность сигнала увеличится в M раз, то уровень сигнала увеличится на N децибел, в частности:

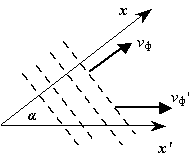
  M  =  2    3    5   10   100   1000   10000  ...
  N  =  3   4,8   7   10    20    30     40    ...

Скорость изменения фазы акустической волны, т.е. переменного угла θ (t, x) = ωt – kx + φ, стоящего под знаком косинуса в выржении для гармонического закона, называется фазовой скоростью. В случае простого гармонического колебания она в точности совпадает со скоростью звука ( v_ф = c = ω / k ). Если рассматривать скорость перемещения волновых гребней (пунктирные линии) вдоль некоторой оси x' (рис. 9), образующей угол α с осью x, то она окажется выше, так как v'_ф = v_ф / cos α. Здесь уместно следующее сравнение. Как известно, скорость движения границы тени при утреннем восходе и вечернем заходе солнца намного выше, чем в полдень, так как косые лучи перемещаются быстрее прямых.

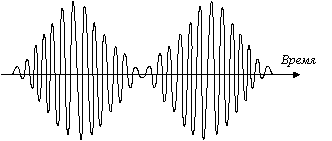
Рис. 9. Распространение плоских волн (пунктирные линии) с фазовой скоростью v_ф вдоль оси x и со скоростью v'_ф вдоль оси x' (v'_ф > v_ф).

Наряду с фазовой скоростью существует групповая, с которой перемещается группа или цуг волн (рис. 10). Эти две скорости совпадают; v_ф = v_гр , если цуги образованы суммой двух или нескольких гармонических колебаний. В нелинейной среде, где нарушается принцип суперпозиций, или в дисперсионной среде с тепловыми потерями равенство переходит в неравенство : v_ф > v_гр . Далее наметим математический подход к нахождению групповой скорости.

Рис. 10. Волновые пакеты (биения),
образованный двумя гармоническими колебаниями,
в частности, падающим и отраженным сигналом.

Выше было дано определение фазовой скорости, вытекающее из математической записи фазы гармонического колебания: θ = ωt – kx + φ. Если имеются два гармонических колебания с небольшой разницей в частоте, то возникает сложное колебание с биениями (см. рис. 10), фаза которого можно представить в виде следующего выражения:

θ = (ω_о ± Δω) t – (k_о ± Δk) x + φ,

где ω_о — среднее значение угловой скорости, k_о — среднее значение волнового числа, Δω и Δk — соответствующие отклонения от средних значений. В целом это сложное колебание будет распространяться в среде с фазовой скоростью   v_ф = ω_о / k_о , но его огибающая (т.е., собственно, сами биения) будут двигаться уже с групповой скоростью   v_гр = Δω / Δk .

В дисперсных средах все резко усложняется, хотя математическое определение групповой скорости, как   v_гр = dω / dk ,   сохраняется прежним. Для нахождения групповой скорости в каждом конкретном случае требуется знать так называемый дисперсионный закон :   ω = ω ( k ) ,   который зачастую не так просто отыскать для реальных веществ. Поскольку с частотой однозначно связана энергия ( E ), а с волновым вектором — импульс ( p ), то закон дисперсии отображает распределение энергии в импульсном пространстве возбужденной среды:   E = E ( p ).

Идеальные условия соблюдения гармоничности колебаний могут нарушаться многими способами. Им будут соответствовать и различная природа волновых групп, на которые распадается исходное возбуждение среды. Так, брошенный в воду камень образует на поверхности воды затухающие колебания (рис. 11), скорость которых определяется в основном силами поверхностного натяжения, если камнем является крохотная песчинка, или силами гравитации, если камень больших размеров и образованные им волны колеблют весомые объемы воды. Еще на колебания водной глади может оказывать воздействие постоянно дующий ветер или близость дна (граница глубины).

Рис. 11. Колебания водной глади,
возникшие от падения камня в воду.

Первый большой всплеск вызовет череду волн, амплитуда которых начнет быстро спадать. Большая амплитуда создает нелинейную ситуацию, которая описывается сложными математическими уравнениями. В области первого всплеска образуются волны, которые равноускоренно удаляются от точки падания камня с последовательными ускорениями, равными

а₁ = 0,325g,       а₂ = 0,069g,       а₃ = …,

где g — ускорение свободного падения. Когда амплитуда волны выйдет на какую-то более или менее постоянную величину, закон дисперсии на отдаленном от точки падения камня участке можно представить достаточно простой формулой:

,

где δ — коэффициент поверхностного натяжения. Для гравитационных поверхностных волн на глубокой воде параметром дисперсии является ускорение свободного падения g (ω ² = gk); для капиллярных волн — отношение коэффициента поверхностного натяжения δ к плотности жидкости δ (ω ² = k³ δ / ρ ).

Фазовая и групповая скорость здесь ищутся в соответствии с выше приведенными формулами:   v_ф = ω / k   и   v_гр = dω / dk .   Для чисто гравитационного случая, когда величиной δ можно пренебречь,   v_ф = 2v_гр = g / ω . Минимальное значение фазовой скорости v_ф = 23 см/с достигается при   λ_о = 1,7 см.   При длине волны   λ > λ_о   имеем гравитационные волны, при   λ < λ_о   — капиллярные.

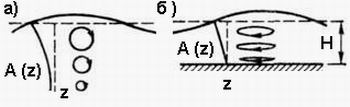
Вертикальные колебания поверхности возникают как следствие кругового движения жидкости на глубине (рис. 12а). Смещения молекул в плоскости рисунка определяются следующими формулами:

a ( z, x, t ) = A (z) cos (ωt – kx) ,   A (z) = A_о exp ( –kz),

где A_о — амплитуда смещения, A (z ) — радиус окружности вращения молекул, который зависит от глубины z.

Рис. 12. Колебания поверхности воды на глубине (а)
и на мелководье (б)

Если глубина ограничена дном   z = H   (рис. 12б ), то круговые движения молекул деформируются в эллиптические, вытянутые по горизонтали:

A ( z, H ) = A_оsh [( H – z ) k ] / sh ( H k ) .

и в законе дисперсии фигурирует значение H :

.

Для коротких волн, когда H k >> 1, гиперболический тангенс ( th H k ) ≈ 1 , так что дно не будет помехой для их распространения. Но для длинных волн ( H k << 1 ) дисперсионный закон приобретает вид: ω = k ( g H ) ^½ и групповая скорость равна фазовой:

v_гр = v_ф = ( g H ) ^½ .

Итак, мы проанализировали влияние глубины H на величину групповой скорости для идеально гофрированных волн. Наличие ветра изменит форму колебаний и для ее математического описания придется внести существенные изменения.

В акустических системах тоже не существует какой-то одной универсальной формулы для нахождения закона дисперсии и групповой скорости. Всякий раз нужно исследовать конкретные физические условия, которые не всегда просто установить и математически описать.

Вообще, любая модель сложного физического процесса почти всегда является упрощением и одной из возможных вариантов. Тем не менее, имеются какие-то общие соображения, справедливые для всех без исключения нелинейных систем с затуханиями. К ним, в частности, относится быстрое угасание высших гармоник по сравнению с низшими. Как это нужно понимать?

Дело в том, что Фурье дал методику разложения любого сколь угодно сложного колебания на сумму синусоидальных составляющих (гармоник). Число гармоник может быть конечным или бесконечным. На рис. 13 показана сумма четырех гармоник с конкретными числовыми параметрами (пример взят из [1]):

u = A₀ + A₁ cos ( ωt + θ₁) + A₂ cos (2ωt + θ₂) +
+ A₃ cos (3ωt + θ₃) + A₄ cos (4ωt + θ₄)

A₀ / A₁ = 0,44 ,     A₂ / A₁ = 0,97 ,     A₃ / A₁ = 0,47 ,     A₄ / A₁ = 0,14 ;
θ₁ = – 58° ,     θ₂ = – 151° ,     θ₃ = + 124° ,     θ₄ = + 86° .

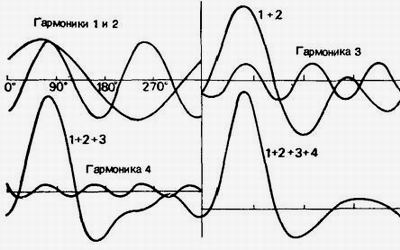
Рис. 13. Фурье-анализ: разложение
сложного колебания на четыре гармоники

Так вот, в среде с затуханием четвертая гармоника начнет исчезать первой. В результате исходный сигнал (1 + 2 + 3 + 4) превратится в искаженный сигнал (1 + 2 + 3). Затем он превратится в сигнал (1 + 2) и последней исчезнет самая первая гармоника.

Всякое возбуждение в среде можно развернуть либо во времени, либо по оси частот. Так как период и частота колебаний находятся во взаимно обратной зависимости (T = 1 / f ), то говорят либо о прямом ( t ), либо об обратном ( f ) представлении сигнала (рис. 14, взят из [3, с. 16] ), которые между собой связаны преобразованиями Фурье. Прямое преобразование Фурье позволяет по известной импульсной функции p (t) найти неизвестный спектр G ( f ); обратное преобразование, действует, наоборот, от G ( f ) к p (t).

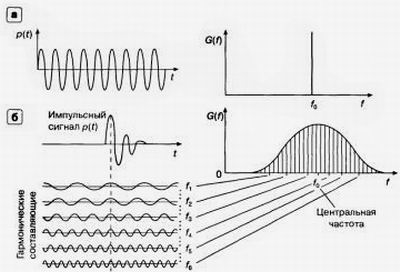
Рис. 14. Прямое ( t ) и обратное ( f ) представление сигналов: а) простое гармоническое колебание, б) импульсный сигнал, который можно представить совокупностью гармоник. Здесь p (t) — функция, описывающая изменения формы импульса во времени; G ( f ) — спектральная функция.

Добавим, что обычно пользуются угловой частотой ω = 2π f, а не параметром f. Аналогичная связка через преобразования Фурье действует в отношении длины волны ( λ ) и волнового числа k = 2π / λ (собственно, сам коэффициент 2π диктуется Фурье-преобразованием). Пространственным Фурье-преобразованием удобно пользоваться, когда имеешь дело, например, с дисперсией электронов на кристаллической решетке, которую тоже изображают в прямом и обратном пространстве. В этом случае длина волны ( λ ) электронной ψ-функции совпадает с периодом элементарной решетки. Более глубокий смысл этих пространств и преобразований раскрывается в ряде разделов «Конструктивной математики» (начать можно с раздела Структурный фактор ).

Выше уже говорилось, что сложный сигнал можно разложить в ряды Фурье, состоящие из совокупности гармонических колебаний с различной амплитудой, частотой и начальной фазой (рис. 14б). Обычно, на средние или центральные частоты приходится максимальная мощность (амплитуда) сигнала. Поэтому в большинстве случаев спектры имеют колоколообразный вид.

Говорилось также, что колебания с малой длиной волны, сопоставимой с размерами молекул и межмолекулярными расстояниями, испытывают наибольшее затухание и торможение. Другими словами, спектры в первую очередь теряют правый высокочастотный «хвост». Это оборачивается тем, что исходное возбуждение при прохождении через дисперсную среду расплывается, его острые углы округляются, как это показано на рис. 15.

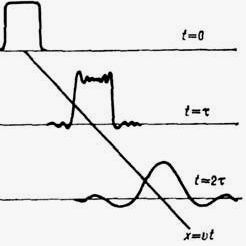
Рис. 15. Расплывание импульса за счет
затухания в среде высших гармоник.

Многие из нас проходили обследование с помощью ультразвука. Жидкости различной консистенции, сосудистая система кровотоков, волокна мышц, жировые отложения и многие другие ткани образуют сложную биологическую структуру, способную расщепить одиночный исходный сигнал на группу сигналов (рис. 16).

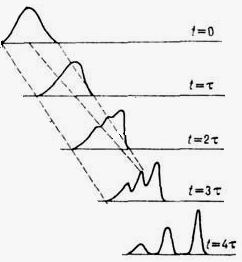
Рис. 16. Расщепление одиночного возбуждения на
несколько вторичных импульсов, перемещающихся
с одной групповой скоростью.

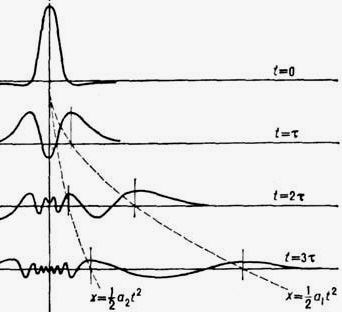
Может случиться и так, что каждый вторичный импульс, возникший в результате расщепления исходного, начнет двигаться в более или менее однородной среде со своей собственной групповой скоростью v₁ , v₂, v₃ и т.д. (рис. 17).

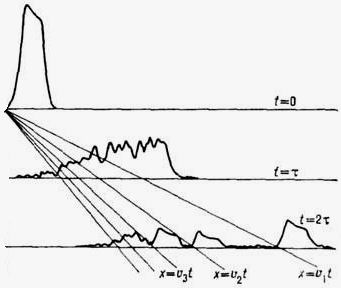
Рис. 17. Движение вторичных импульсов
с различными групповыми скоростями.

Во всех таких случаях фазовая скорость превращается в некую абстракцию или, по крайней мере, перестает играть сколько-нибудь значимую роль, поскольку импульсы — а вместе с ними и энергия возбуждения — распространяются в среде с групповой скоростью.

Понятие о затухании, как строго количественную величину, введем через уравнение движения материальной точки, как это сделано в [1].

Пусть частица среды массой m колеблется по прямой около своего положения равновесия Р. Если y — расстояние частицы от точки Р, то величина возвращающей силы, направленной к Р, пропорциональна y и равна, Ky, где K — некоторая положительная постоянная. Под действием этой возвращающей силы частица совершает колебательные движения с постоянно меняющимся ускорением. Такое движение будет описываться уравнением

md²y/dt² = –Ky,

которое может быть представлено в виде

d²y/dt² + ω²y = 0,

где ω² = K/m — квадрат угловой частоты колебаний. Решением для этого уравнения будет тригонометрическая функция следующего вида:

y = A cos ωt + B sin ωt .

Значения констант A и B ищется из начальных условий для функции y и ее первой производной:

dy/dt = –ωA sin ωt + ωB cos ωt.

Если в качестве примера рассмотреть простой маятник, то начальными условиями для него могут выступать три равенства:

t = 0,     y = a,     dy/dt = 0.

Эти условия приводят к двум тригонометрическим выражениям, графики которых представлены на рис. 18:

y = a cos ωt     и     dy/dt = –ωa sin ωt .

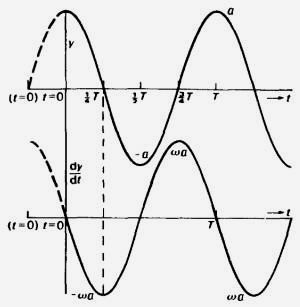
Рис. 18. Гармонические колебания при начальных
условиях: t = 0,     y = a,     dy/dt = 0

Начальные условия можно изменить:

t = 0,     y = 0,     dy/dt = V,

что соответствует случаю движения маятника из положения равновесия со скоростью V. Тогда A = 0,   ωB = V, следовательно,

y = (V/ω) sin ωt     и     dy/dt = V cos ωt.

В общем случае решение можно свести к выражениям:

y = A ' cos (ω t – φ);     A ' = (A ² + B ²) ½ ,   φ = arctg (B/A) .

Этим выражениям отвечают графики, показанные на рис. 19.

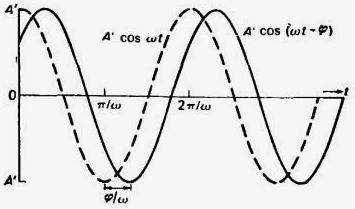
Рис. 19. Гармоническое колебание
y = A ' cos (ω t – φ)

Для всякого гармонического колебания энергия остается неизменной. В частности, для маятника массой m, подвешенного на нити длиной l, колеблющегося с частотой ω² = g/l, сумма кинетической и потенциальной энергии есть константа:

E = mv²/2 + mgz = a²mg/2l = const.

Если в системе действует демпфирующая сила, пропорциональная скорости, то уравнение движения частицы добавится третий член, определяющий характер затухания:

md²y/dt² = –Ky – Cdy/dt,

или

d²y/dt² + 2βy/dt + ω²y = 0

где C — константа, 2β = C/m, ω² = K/m

Здесь возможны три случая.

Случай A. Если β < ω , то решение уравнения движения с затуханием имеет вид:

y = a sin ω₁t

где
ω²₁ = ω² – β² — собственная частота затухающего колебания;
a = (V/ω₁) exp (– βt) — затухающая амплитуда.

Множитель exp (– βT₁ ) называется коэффициентом затухания.

Случай Б. Если β > ω , то решение имеет вид:

y = a [exp (nt) – exp (–nt)] ,

где n² = β² – ω² ;       a = (V/2n ) exp (– βt).

Такие колебания называются со сверхкритическим затуханием.

Случай В. Если β = ω , то решение имеет вид:

y = Vt exp (– βt).

Такие колебания называются с критическим затуханием.

Всем трем случаям соответствуют графики (рис. 20).

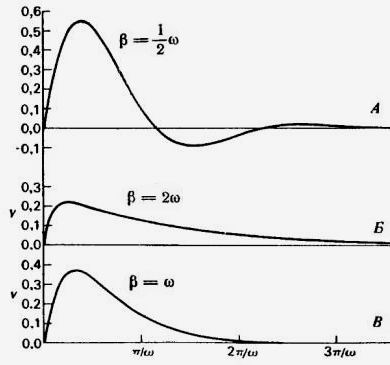
Рис. 20. Графики зависимости y( t )
для трех значений β (случаи А, Б и В).

Независимо от характера затухания вводят константу затухания: τ — это то время, в течение которого амплитуда колебаний уменьшается в e = 2,718 раз. Отношение периода колебаний ( T ) к постоянной затухания (τ) называется декрементом — D = T / τ.

Характер затухания раскрывается через временную переменную t; на практике же пользуются коэффициентом затухания, показывающим экспоненциальный закон ослабления давления в зависимости от глубины проникновения x ультразвукового излучения:

P = P_о exp ( –αx ),

где P_о и P — максимальное исходное и текущее давление в среде, α — коэффициент затухания, зависящий от глубины проникновения.

Затухание (как и всякий перепад давления) измеряется в децибелах, отнесенных к единице расстояния. При этом указывается частота сигнала, например: 5 дБ/см на частоте 3 МГц. С увеличением частоты сигнала затухание, естественно, нарастает, причем в костных тканях это происходит быстрее, чем в мягких, например, в мышцах, легких или печени. Однако в легких за счет пористости ткани затухание будет максимальным (рис. 21а взят из [2] и рис. 21б взят из [3, с. 24] ).

а


б

Рис. 21. Графики изменения коэффициентов затухания (α) в зависимости от изменения частоты сигнала ( f ): взято а) из [2] и б) из [3], где 1 — легкие, 2 — кости черепа, 3 — кожа, 4 — мышцы, 5 — мозг взрослого, 6 — мозг ребенка, 7 — печень, 8 — кровь, 9 — вода. Пунктирной кривой показаны средние значения затухания для мягких тканей.

По данным источника [2] при f = 1 МГц величина коэффициента затухания в единицах 1/см для крови составляет 0,023 , жира — 0,044-0,09 , кожи — 0,14-0,66 , хрящей — 0,58 , костей черепа — 1,5-2,2 и легких — 3,5-5.

Из-за разности в групповой скорости звука, исходные импульсы не только ослабляются, но и заметно искажаются в виду дрейфа средней частоты в область уменьшения. Эту закономерность можно проследить на графиках смещения влево спектров отражения в зависимости от роста глубины проникновения импульсов (рис. 22, взят из [3, с. 25] ).

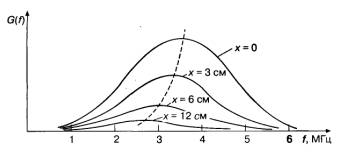
Рис. 22. С увеличением глубины x проникновения исходных импульсов происходит ослабление и смещение их спектров G (f ) влево. Пунктирной линией обозначена траектория смещения средней частоты импульсов в область уменьшения.

Из рис. 22 «видно, что если на самых малых глубинах спектр изменяется незначительно, то с увеличением глубины кривая, описывающая форму спектра, заметно сдвигается влево. Если центральная частота излучаемого сигнала была равна 3,5 МГц, то на глубине 6 см она равна 3,1 МГц, а на глубине 12 см она близка к 2,8 МГц. Смещение спектра эхо-сигнала в сторону низких частот с увеличением глубины должно учитываться при создании диагностического прибора. Поэтому во всех современных УЗ приборах используется автоматическая подстройка частоты (АПЧ) приемника эхо-сигналов в зависимости от глубины или, что то же самое, от времени прихода эхо-сигналов» [3, с. 26].

Этих первоначальных сведений из области акустики вполне достаточно, чтобы разобраться в работе устройств, функционирующих в ультразвуковом диапазоне.

---

1. Каро К., Педли Т., Шротер Р., Сид У. Механика кровообращения. — М.: Мир, 1981.
2. Физическая энциклопедия. http://www.femto.com.ua
3. Осипов Л.В. Ультразвуковые диагностические приборы: Практическое руководство для пользователей. — М.: Видар, 1999.