
Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
2.5. Пространственные группы и двойственность
Моделирование волновых процессов. Эффект Доплера
Задача этого подраздела состоит в том, чтобы на примере модели простого волнового процесса, который называется Эффект Доплера, показать преимущества конструктивного подхода в физике. Всякий конструктивист в области физики так же, как и в области математики, будет создавать свои конструкции с заданными свойствами и сверять их с тем, что имеет место в действительности. Построение наглядной модели — лучше, если она будет пространственно-механической, — вот, в чем успех теоретических поисков. Только ясное образное представление физического процесса в самых тончайших деталях — это единственное, что может удовлетворить пытливого конструктивиста. Он не станет решать общие задачи абстрактного содержания, скорее всего, он займется решением конкретных проблем, например, следующего содержания.
В полете футбольный мяч испытывает сопротивление воздуха, которое можно перенести на массу мяча, приписав ей эффективное значение. Чем выше скорость движения мяча, тем больше его эффективная масса. Возникает вопрос, насколько близка эта формула зависимости эффективной массы от увеличения скорости движения к известной релятивистской формуле для массы, если принять константу c за скорость звука? Возьмем другую проблему. Заметив, что вихрь воздушной или водной массы занимает определенное и достаточно устойчивое положение в пространстве, как если бы он обладал некоторой собственной инерцией к внешним воздействиям, конструктивист может задаться вопросом: а будет ли масса вращающегося объекта (а значит, и его гравитационное поле) несколько больше массы этого же объекта, но уже не вращающегося? Если да, то какова зависимость изменения массы объекта от скорости его вращения?
Очевидно, что ответы на сформулированные вопросы связаны с отчетливыми представлениями о силах и динамических напряжениях, действующих в сплошной среде. Поступательное или вихревое движение объектов, находящихся в сплошной среде, явление довольно сложное, чтобы тут же приниматься за немедленное решение данной задачи. Сейчас мы рассмотрим куда более простую физическую задачку, связанную с динамикой волн.
На рис. 2.41 показаны волны, испущенные движущимся со скоростью v источником колебаний i. Вдоль пунктирной линии длина волны λ' будет несколько меньше собственной длины волны λ, испущенной неподвижным источником, а частота колебаний f ', соответственно, — выше собственной частоты f. Частота колебаний связана с периодом колебаний: τ = 1/f и τ' = 1/f '. Из геометрии чертежа несложно найти соотношения, связывающие штрихованные и нештрихованные величины:
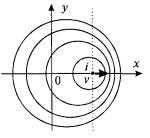
Рис. 2.41
λ' = λ
, f ' =
, τ' = τ
.
Выписанные формулы в релятивистской теории получили названия поперечного доплер-эффекта, с которым, согласно нынешним представлениям, связано так называемое замедление времени (t'), наблюдающееся у быстро перемещающихся объектов. Предлагалось по измерению величин λ', f ', τ' судить о справедливости релятивистской физики. В классической же физике для движущегося источника и покоящегося наблюдателя имеются другие формулы:
λ' = λ(1 – βcosθ), f ' = f /(1 – βcosθ), τ' = τ(1 – βcosθ),
которые при углах θ = ± π/2 никакого поперечного доплер-эффекта не дают, так как при этом значении угла формулы переходят в равенства: λ' = λ, f ' = f и τ' = τ. Спрашивается, можно ли совместить данные результаты с модельными представлениями о распространении волн в среде, учитывая, что природа волн и скорость их распространения абсолютно не влияют на геометрию чертежа?
Чтобы ответить на этот вопрос, детально проследим за динамикой волн и на ее основе получим те формулы, которые диктует нам геометрическая модель. С этой целью обратимся к рис. 2.42, где изображен единственный волновой фронт на момент времени, когда он достиг точки A, и источник колебаний i, который вот-вот испустит новый волновой фронт. Следовательно, истинной длиной волны будет не расстояние 0A = λ (эта длина соответствует покоящемуся источнику), а расстояние AB = λ', при этом пройденное источником расстояние будет равно: 0B = βλ, где β = v/c, v — скорость движения источника, c — скорость распространения волнового фронта. Далее нам нужно выразить длину волны λ через λ', используя элементарное геометрическое соотношение:
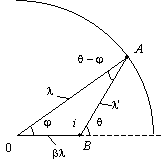
Рис. 2.42
λ' = λ cos (θ – φ) + βλ cos (π – θ).
Отсюда имеем:
λ' = λ [cos (θ – φ) – β cos θ].
В последней формуле фигурируют два угла; это неудобно, с точки зрения интерпретации формулы. Но мы можем воспользоваться теоремой синусов:
или sin (θ – φ) = β sinθ.
Тогда формула для λ' приобретет вид:
λ' = λ (
– β cos θ).
Если воспользоваться теоремой косинусов:
λ'2 = λ2 – 2βλ2cos θ + β2λ2,
то получим другую модификацию формулы эффекта Доплера:
λ' = λ
.
Угол θ является углом наблюдения длины волны λ', следовательно, нам удобно воспользоваться формулой
λ' = λ (
– β cos θ);
при θ = ± π/2 имеем λ' = λ
, что и является сутью поперечного эффекта Доплера.
Для движущегося наблюдателя и покоящегося источника формула для измененной длины волны λ' будет выглядеть по-другому:
λ' = λ
.
Если источник и наблюдатель движутся одновременно, то имеем:
.
Из разложения функций в ряды известны следующие приближенные равенства:
,
,
.
Применяя эти формулы соответствующим образом к правым и левым частям ниже выписанных приближенных выражений, можно убедиться в их справедливости:
– β2cos θ2 »
,
»
.
Таким образом, формулы, описывающие классический доплер-эффект, при углах, близких к величинам θ1 = θ2 = ± π/2, достаточно точно совпадают с релятивистскими. Отсюда, если речь идет об эффекте Доплера, появляется возможность интерпретации релятивистских явлений через представления классической физики. Двойственность эффекта Доплера состоит в симметрии двух последних формул для движущегося источника и приемника колебаний.
Добавление
Со школьной скамьи нам знакома нехитрая формула, которой пользуются и профессиональные ученые:
. (1)
Формула (1) описывает принятую длину волны ( λ' ), если известна собственная длина волны ( λ ) движущегося с относительной скоростью ( β = v/c ) источника колебаний и угол наблюдения ( φ ). Не станем пока сосредотачиваться на вопросе, как выводится формула (1). Однако уже сейчас полезно задаться вопросом, почему выражение (1) никак не реагирует на ситуацию, возникающую при появлении ударной волны, т.е. когда скорость источника становится больше скорости распространения колебаний ( β > 1 ).
 |
 |
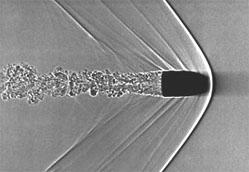
| Рис. 3а. Фотография летящей пули, на которой виден фронт ударной волны. | Рис. 3б. Фотография самолета FA-18, на которой тоже виден конус ударной волны. |
Еще в XIX столетии Эрнст Мах, изучая движение пули, движущейся в воздухе быстрее звука (рис. 3а), установил, что угол при вершине конуса ударной волны определяется относительной скоростью β:
sin θ = 1/β = c/v (2)
(отсюда параметр β часто называют числом Маха). Формулой (2) пользуются конструкторы сверхзвуковых самолетов. На рис. 3б приведена фотография самолета FA-18, летящего быстрее звука. Вблизи летального аппарата виден светлый конус. Дело в том, что сразу же за ударной волной создается зона пониженного давления, в которой происходит мгновенная конденсация паров влаги (этот принцип лежит в основе работы камеры Вилсона, в которой можно видеть треки микрочастиц). Зная скорость звука (c = 331 м/с) и угол θ, мы можем по формуле (2) вычислить скорость самолета. Судя по форме конуса, изображенного на нашей фотографии, самолет FA-18 летит не намного быстрее звука, порядка 350 м/с. Непосредственное измерение угла по изображению пули даёт величину порядка θ = 60º, следовательно, её скорость близка к 380 м/с. Следует иметь в виду, что формулу (2) нельзя получить из формулы (1); она выводится из соображений, продиктованных рис. 4.
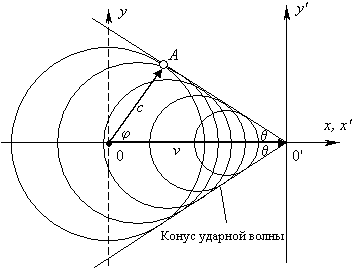 |
Рис. 4. Чертеж, позволяющий получить формулу (2) для определения угла θ при вершине конуса ударной волны
...Даже без всякого экспериментирования, чисто априорно можно было бы догадаться, что формула, описывающая эффект Доплера, должна представлять собой математическое выражение векторного сложения двух скоростей — v и c. Увы, никто не вспомнил, что формула (1) была получена в сильном приближении, дающем совершенно непозволительное отклонение от реально наблюдаемых явлений. Давайте сейчас, не отвлекаясь на допущенные автором формулы (1) просчеты, сами найдем точное выражение для суммы двух векторов, тем более, что это не займет много места.
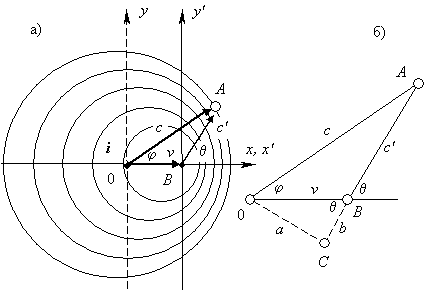 |
Рис. 6. Чертеж (а) представляет собой застывшее изображение анимационного изображения, показанного на рис. 1а. Пока волновой фронт, испущенный из точки 0, дойдет до точки А, источник колебаний i окажется в точке В. Чтобы найти выражения для векторной суммы векторов v и c, на чертеже (б) показан вспомогательный прямоугольный треугольник.
На рис. 6а вычерчен «застывший» в произвольный момент динамический процесс, показанный на рис. 1а. На одной из окружностей — неважно какой, поскольку все треугольники 0АВ будут подобными, — выбрана точка А. Стороны треугольника 0А и 0В соответствуют скоростям v и c; нужно по двум сторонам треугольника 0АВ найти третью — АВ. Для решения этой задачи треугольник 0АВ достраиваем до прямоугольного 0АС, как показано на рис. 6б. Из последнего чертежа находим отрезки a = v sin θ и b = v cos θ. По теореме Пифагора составляем равенство:
.
Если в последнее выражение подставить значения a и b, получим искомую скорость c' :
.
Умножая обе части равенства на период колебаний Т, получаем изменившуюся за счет эффекта Доплера длину волны λ', которую удобно выразить через параметр β:
. (4)
Формула (4) есть истинное, абсолютно точное выражение, описывающее эффект Доплера для любых значений параметра β. То, что формула (4) является именно выражением для суммы двух векторов v и c, можно легко убедиться, если ее представить через угол φ между v и c. Для этого нужно к треугольнику 0АВ применить теорему косинусов:
. (5)
С точки зрения математики выражения (4) и (5) отражают один и тот же математический факт; разница между ними примерно такая же, как между формулами (2) и (3). Однако с точки зрения физики было бы ошибкой считать φ углом наблюдения (рис. 4 и 6); им является угол θ. Это прекрасно видно в случае, когда возникает ударная волна. На анимационном рис. 1б видно, как конус ударной волны перемещается вместе с источником колебаний. Значит, для получения формулы Маха (2) и тесно связанной с ней формулой (4) нужно перейти из неподвижной системы координат (x, y) в штрихованную систему координат (x', y'), начало которой совмещено с движущимся источником волн.
Для получения формулы (4) никакого наблюдателя или приемника не требуется. Система концентрических колец со смещенными центрами образуется и без них. Главное, что здесь нужно, это выразить произвольно взятую окружность корректным образом. Старая формула (1), как мы увидим ниже, является уравнением кардиоиды в полярной системе координат, а полученное нами выражение (4) является уравнением окружности. Для этого уравнения угол θ является свободным параметром или аргументом, а воспринимаемая приемником длина волны λ' или сторона АВ, изображенного на рис. 6а треугольника, является радиус-вектором или функцией для указанного аргумента.
В самом деле, из рис. 6а можно записать:
0А = λ, 0В = βλ и АВ = λ'.
В декартовой системе координат (x', y') с началом в центре В, уравнение окружности выглядит следующим образом:
(x' + βλ)2 + (y')2 = λ2.
Произведем переход от декартовых координат к полярным по формулам:
(λ')2 = (x')2 + (y')2, x' = λ'cosθ, y' = λ'sinθ.
Тогда наше уравнение окружности будет иметь вид:
(λ')2 + 2βλλ'cosθ – λ2(1 – β2) = 0.
Перед нами обыкновенное квадратное уравнение, решая которое относительно неизвестной λ', мы получаем формулу (4).
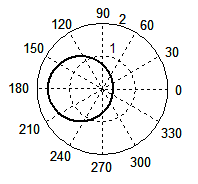
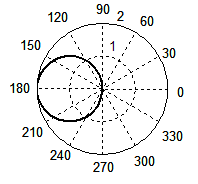
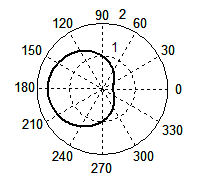
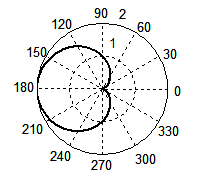
Окружность получается и в том случае, если для функции λ' выражения (4) построить графики зависимости от аргумента θ, меняющийся в пределах от 0 до 2π. Графики этой зависимости (рис. 7) для β = 3/4 (а) и β = 1 (б) лишний раз подтверждает, что мы имеем дело действительно с окружностями, которые можно видеть, например, на поверхности озера, когда по ней бежит водомер. Однако традиционное выражение (1), приводимое во всех сегодняшних справочниках и учебниках, окружности не дает. При тех же значениях β волновой фронт как функция λ' от аргумента θ порождает кривые (в, г), которые в математике называются кардиоидами.
 (a) (a) |
 (б) (б) |
 (в) (в) |
 (г) (г) |
 (д) (д) |
 (е) (е) |
 (ж) (ж) |
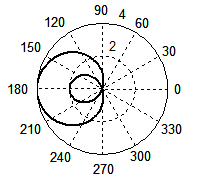 (з) (з) |
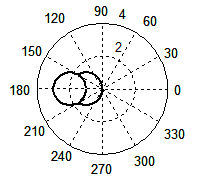
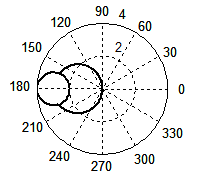
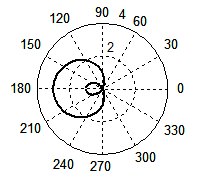
Рис. 7. Форма волнового фронта при Доплер-эффекте, рассчитанная по формуле (4) при β = 3/4 (а), β = 1 (б); по формуле (1) при β = 3/4 (в), β = 1 (г). Для случая появления ударной волны: по формуле (4) при β = 2 (д), β = 3 (е); по формуле (1) при β = 2 (ж), β = 3 (з).
Самое важное, что точная формула (4) прекрасно работает и в случае ударной волны. Волновой фронт сохраняет форму окружности при любом значении β, в частности, при β = 2 (д) и β = 3 (е). Обратите внимание, радиусы обеих окружностей одинаковые и равны единице, только в случае (д) центр окружности отнесен на расстояние, равное двум, а для случая (е) — трем, что вполне логично. Таким образом, формула (4) в точности следует тому, что повсеместно наблюдается в природе: с увеличением скорости движения источника слева направо круги, естественно, всё дальше и дальше смещаются влево от источника. Формула Маха (2) также естественно вытекает из формулы (4). Если подкоренное выражение окажется отрицательным, то корни из него будут мнимыми. Мнимые величины не имеют физического смысла, поэтому на подкоренное выражение накладывается условие:
1 – β2 sin2θ ≥ 0, sinθ ≤ ±1/β или θ ≤ arcsin (±1/β).
На графиках (д) и (е) показаны неполные окружности, которые не имеют определенного физического смысла. Тем не менее, эти мнимые волны были оставлены на чертеже, поскольку их концы точно указывают точки соприкосновения реальных волн с конусом ударной волны. На двух последних графиках изображены кривые, вычерченные в соответствии с традиционной формулой (1) при тех же значениях β = 2 (ж) и β = 3 (з). Как видим, ничего близкого с действительностью эти графики не имеют.
Вопросы эффекта Доплера рассматриваются также на следующих страницах:
- Введение в акустику. Природа звука и ультразвука
- Введение в конструктивную физику
- О формуле, описывающей классический эффект Доплера
- Ошибочность релятивистской формулы Доплера
- Квантовая теория Доплер-эффекта
- Эксперимент Майкельсона – Морли
- Лекция 4. Эффект Доплера
- Часто задаваемые вопросы по эффекту Доплера
- Идиотский расчет эффекта Доплера
- Использование в медицине поперечного эффекта Доплера для ультразвуковой диагностики сердечно-сосудистой системы
- Эффект сдвига воспринимаемой длины волны в красную область
- Моделирование волновых процессов. Эффект Доплера