
Ошибочность релятивистской формулы Доплера
Олег Акимов
Свет и звук распространяются однотипно
Скорость распространения звука не зависит от состояния его источника — движется он или покоится. Фронт акустической волны как бы забывает о своем источнике и всецело вверяет себя среде. Аналогично ведет себя фронт оптической волны по отношению к излучателю света. Однако теория относительности внесла сумятицу в умы физиков, когда речь заходит о движении приемника света.
Для звука скорость распространения в среде складывается со скоростью приемника в соответствии с правилом векторного сложения. Например, грохот взрыва водитель автомобиля, движущегося к точке взрыва, услышит раньше, чем милиционер, неподвижно стоящий на перекрестке дорог. Это и понятно: пока акустическая волна распространяется в пространстве, автомобиль преодолеет какое-то расстояние. Следовательно, водитель окажется ближе к источнику звука, чем неподвижный постовой. Здесь мы имеем полное согласие здравой логики с классической физикой. Но со вспышкой света от этого взрыва происходят какие-то чудеса. Движущейся автомобилист и неподвижный милиционер, согласно теории относительности, зафиксируют ее строго одновременно! Разве такое возможно?
Подобно тому, как священнослужители запрещают думать над образом Бога, релятивисты противятся представлять физические процессы, разворачивающиеся в реальном пространстве и времени. Они апеллируют к своим священным формулам и говорят о трансцендентном мире, в котором здравый смысл бессилен. Тем не менее они не отрицают, что свет распространяется в пространстве намного быстрее звука. Естественно также, что ему потребуется какое-то время Δτ, чтобы достичь приемника. За это время Δτ автомобилист подъедет ближе к точке взрыва. Следовательно, он чуть-чуть раньше увидит вспышку, чем оставшийся позади него милиционер. А это как раз и означает, что скорость движения автомобиля прибавится к скорости распространения светового фронта, что, однако, уже противоречит теории относительности.
Релятивисты оправдывают свою противоестественную кинематику отрицательным результатом эксперимента Майкельсона – Морли, который заставил их отказаться от эфирной среды. Эфир для света играл роль воздуха для звука, в результате все оптические формулы совпадали с акустическими. Мы не станем сейчас разбирать ошибки истолкования этого опыта релятивистами (см. Эксперимент Майкельсона – Морли). Заметим лишь, что релятивистская логика противоречит самым элементарным фактам, с которыми человек столкнулся сразу же, как только заинтересовался скоростью распространения света (см. Главный аргумент против теории относительности). В данном разделе мы детально проанализируем явление, известное под названием «эффект Доплера», и посмотрим, как сосуществуют формулы Доплера для классической и релятивистской физики. Напомним, что традиционные формулы для акустических волн слишком грубы и во многих случаях не пригодны даже для классической физики (см. О формуле, описывающей классический эффект Доплера). Таким образом, наше внимание будет сосредоточено на релятивистских формулах.
На рис. 1 показан процесс распространения волн (акустических или оптических — не важно), когда (а) источник колебаний движется слева направо со скоростью меньше скорости распространения волн в среде (v < c). На рисунке (б) изображен тот же самый процесс распространения, но уже при условии, когда источник волн движется быстрее, чем распространяются волны (v > c).
 |
 |
| Рис. 1а. Источник возбуждения среды движется слева направо со скоростью меньше скорости распространения возбуждения (v < c). | Рис. 1б. Источник возбуждения движется быстрее, чем распространяется возбуждение в среде (v > c). При этом возникает так называемый конус ударной волны |
Наблюдая за процессом распространения волн возбуждения на обоих анимационных рисунках, можно заметить, что расходящиеся во все стороны круги не меняют своего центра. Источник возбуждает неподвижную точку среды, лежащую на горизонтальной линии движения, а дальше возбуждение распространяется во все стороны самостоятельно, не зависимо как от источника, так и приемника возбуждения. Первая возбужденная точка передает импульс напряжения соседним, те, в свою очередь, передают его следующей группе точек и т.д. Такое положение вещей остается в силе при отражении и преломлении волн на границе двух различных сред. Руководствуясь одним этим геометрическим принципом, вытекающим из обязательного условия существования неподвижной среды — носителя волн, Христиан Гюйгенс в XVII столетии в «Трактате о свете» смог удовлетворительным образом объяснить важнейшие оптические явления, в частности, «удивительное преломление лучей в исландских кристаллах».
На рис. 2 приведены четыре характерных чертежа из упомянутой работы замечательного голландского физика, подробно разъясняющих формирование волновых фронтов от неточечного (а) и точечного (б) источника света, а также показывающих отражение (в) и преломление (г) световых волн. Отсюда проистекает принцип Гюйгенса, дающий единственно верное представление о геометрии волновых процессов, который неизменно подтверждается в опытах со звуком и светом. Так, если на пути плоского волнового фронта поставить преграду, в которой имеется маленькое отверстие, соизмеримое с длиной волны, то на другой стороне преграды от этого отверстия будут расходиться сферические волны как от точечного источника.
 (a) (a) |
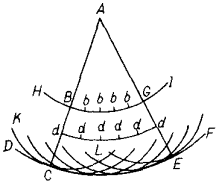 (б) (б) |
 (в) (в) |
 (г) (г) |
Рис. 2. Чертежи из трактата Гюйгенса, разъясняющие геометрию распространения световых волн.
Таким образом, свет (видимое электромагнитное излучение) вызывается не какими-то специальными частицами материи, а именно колебаниями среды. Интерференционная картина лишний раз подтверждает это. Она показывает, как при совпадении фазы колебаний амплитуда волн складывается, а в противофазе — вычитается. Подобное явление не могло бы происходить с частицами, на что указывал и Максвелл. До него выдающийся английский физик, Роберт Гук, мыслящий пространственными образами, критиковал своего соотечественника, Исаака Ньютона, за корпускулярные воззрения на природу света.
Верно, что атому испускают и поглощают электромагнитную энергию квантами, но ошибочно в связи с этим дискретным явлением вводить понятие корпускулы как обособленного кусочка материи — фотона. Частица, лишенная массы, — понятие достаточно абсурдное (вроде бестелесной души), которым физик не должен оперировать. Однако допустимо говорить о квазичастицах, которые ввел Дж. Дж. Томсон. Квазичастица представляет собой волновой пакет, при прохождении которого через вещество происходит распад на отдельные волновые составляющие, участвующие в явлениях интерференции и дифракции. В модели квазичастицы уже не возникает противоречие между волной и частицей, хотя многие нынешние интерпретаторы такой модели продолжают говорить о неком парадоксальном чуде природы.
Такая спекулятивная форма подачи материала с элементами сенсационности весьма характерный феномен современной науки. Например, недавно в журнале Nature за 13 августа 2008 года рассказывалось об опыте с так называемыми спутанными фотонами. Суть его такова. Некий физик Николас Гизин (Nicolas Gisin) из Женевского университета отправил пару спутанных фотонов в противоположные стороны по двум оптическим волокнам на расстояние 9 км на восток и 9 км на запад. На концах волокон он установил детекторы цвета фотонов. При изменении цвета с зеленого на красный одного фотона мгновенно менялся цвет другого. Измерения показали, что для передачи информации о цвете на 18 км в пределах погрешности эксперимента нужна была скорость в 10 тысяч раз больше скорости света.
Очевидно, что в описанном эксперименте мы имеем дело не с двумя спутанными фотонами, а с одним материальным объектом. Нет в природе шариков-фотонов, неких материальных атомов света, которые наподобие горошин летят в полнейшей пустоте или по специально отведенным им оптическим трубопроводам. Но есть электромагнитное возбуждение мировой среды, которое в зависимости от условий может принимать различную конфигурацию и степень локализации. Швейцарский физик имел дело с одним и только одним делокализованным возбуждением, которое ни в коем случае нельзя было представлять как два независимых физических явления. Если цвет меняется синхронно на двух разнесенных детекторах, значит перед нами одно и то же световое явление. Ничего сенсационного здесь нет. Дальше нужно было подумать над пространственно-волновой моделью этого возбуждения, а не публиковать свои сырые и неосмысленные результаты в журнале Nature.
Автор этого журнала хотел удивить своих читателей и, тем самым, в вести их скорее в заблуждение, чем раскрыть им механику явления. Физики-формалисты говорят о «спутанных» фотонах, физики-конструктивисты уверены в их спутанных идеях. Парадоксы в виде существования волны-частицы они находят в природе, между тем, это противоречие прочно сидит у них в мозгу. В описанном эксперименте мы имеем дело не с двумя спутанными фотонами, а с одним материальным объектом. Нет в природе шариков-фотонов, неких материальных атомов света, которые наподобие горошин летят в полнейшей пустоте или по специально отведенным им оптическим трубопроводам. Но есть электромагнитное возбуждение мировой среды, которое в зависимости от условий может принимать различную конфигурацию и степень локализации.
Необычность автор приписал природе физического явления, но не исследователю, ум которого скован противоречием. Между тем всякая парадоксальность в физических понятиях обычно возникает из ошибочности модели исследуемого явления или полного отсутствия о нем представления. Упоминание в статье о чудесах квантовой теории говорит о тех неизлечимых эпистемологических комплексах, которыми страдают романтики ушедшего столетия. Они всё ещё кому-то доказывают, что их формально-феноменологическая теория верна и на что-то годна. Но фактически, данный эксперимент ясно демонстрирует ее полную беспомощность.
Конус ударной волны и
поперечный эффект ДоплераЧасто, имея голые понятия и дефиниции, мы думаем, что понимаем природу физического явления. Но это обманчивое впечатление; без четких пространственно-механических моделей физику явления понять невозможно. Ярким подтверждением этого служит нынешнее достаточно уродливое представление об эффекте Доплера. Для звуковых колебаний изменившаяся длина волны в случае движения только источника колебаний описывается формулой:
. (1)
где λ и λ' — собственная и принятая длина волны, β = v/c — скорость движения источника относительно скорости распространения колебаний, φ — угол между векторами v и c. Если v > c или β > 1, то справедлива формула Маха:
sin θ = 1/β = c/v (2)
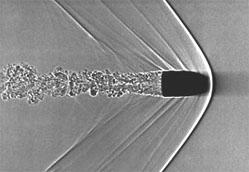
Изучая движение пули, движущейся в воздухе быстрее звука (рис. 3а), Эрнст Мах установил, что угол θ при вершине конуса ударной волны всецело определяется относительной скоростью β (отсюда параметр β часто называют числом Маха). Формулой (2) пользуются конструкторы сверхзвуковых самолетов. На рис. 3б приведена фотография самолета FA-18, летящего быстрее звука. Вблизи летального аппарата виден светлый конус. Дело в том, что сразу же за ударной волной создается зона пониженного давления, в которой происходит мгновенная конденсация паров влаги (этот принцип лежит в основе работы камеры Вилсона, в которой можно видеть треки микрочастиц). Зная скорость звука (c = 331 м/с) и угол θ, мы можем по формуле (2) вычислить скорость самолета.
 |
 |
| Рис. 3а. Фотография летящей пули, на которой виден фронт ударной волны. | Рис. 3б. Фотография самолета FA-18, на которой тоже виден конус ударной волны. |
Непосредственное измерение угла по изображению пули даёт величину порядка θ = 60º, следовательно, её скорость близка к 380 м/с. Судя по форме конуса, изображенного на фотографии, самолет FA-18 летит не намного быстрее звука, порядка 350 м/с. Однако это не совсем так. Дело в том, что реактивные самолеты летают высоко в небе, где скорость звука существенно иная. Следует также иметь в виду, что формулу (2) нельзя получить из формулы (1); она выводится из соображений, продиктованных рис. 4.
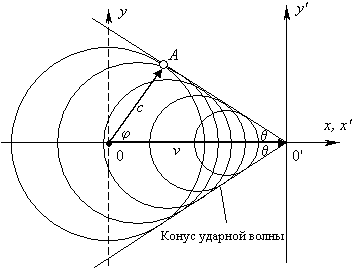 |
Рис. 4. Чертеж, позволяющий получить формулу (2) для определения угла θ при вершине конуса ударной волны
В 1934 году 28-летний П.А. Черенков, аспирант академика С.И. Вавилова, при изучении люминесценции зарегистрировал свечение, исходившее от электронов, летящих в прозрачной среде (H2O, C6H6, C6H12, CS2, CCl4 и др.) со скоростью, превышающей скорость света в данной среде. Этот факт получил название эффекта Вавилова – Черенкова. Примерно через два года ими была получена формулу (3):
cos φ = 1/nβ, φ = arccos (1/nβ) (3)
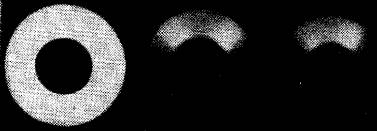
где n — показатель преломление среды. Как рассказал П.А. Черенков [3], наибольшей экспериментальной трудностью оказалось обнаружение направленности излечения: ударная волна распространяется по направлению движения частиц под углом ±φ. После получения фотографий черенковского излучения (рис. 5а) и построения кривых его интенсивности (рис. 5б) написание формулы уже не представляло большой проблемы.
 (a) (a) |
 (б) (б) |
Рис. 5 (а) Фотографии углового распределения интенсивности излучения: обычная люминесценция (снимок слева), свечение этилциннамата (n = 1,58043, снимок в центре), свечение воды (n = 1,3371, снимок справа). (б) Угловые распределения интенсивности для этилциннамата: верхняя кривая соответствует возбуждению свечения комптоновскими электронами от лучей ThC (β = 0,866), нижняя — от Ra (β = 0,866).
Рис. 4 показывает, что выражение (3) является другой тригонометрической формой выражения (2). Таким образом, Черенков и Вавилов, по сути, наткнулись на оптическое явление, которое говорило об идентичной природе электромагнитных и акустических волн. Однако им не пришла в голову мысль об этой параллели.
В 1958 году И.Е. Тамм, П.А. Черенков и И.М. Франк получили Нобелевскую премию за открытие, объяснение и использование эффекта, носящего имя Черенкова (Вавилов умер в 1951 г.). Три десятилетия спустя Франк издал книгу [1], в которой привел все важнейшие статьи, касающиеся данной темы. В первой главе книги «Развитие представлений о природе излучения Вавилова – Черенкова» автор пишет: «Разумеется, опыты Маха с пулей, летящей со сверхзвуковой скоростью, были известны не только И.Е. Тамму, но и мне. По-видимому, мысль об аналогии с волнами Маха не возникала, то ли ошибочно считалось, что к электродинамике эта аналогия неприменима… В те годы преобладающим был квантовый подход к решению проблем излучения быстрых частиц» [1, с. 29]. Франк признался, что в работе Зоммерфельда 1905 года, о которой вспомнил А.Ф. Иоффе, уже рассматривалась данная проблема.
.
В 1958 году И.Е. Тамм, П.А. Черенков и И.М. Франк получили Нобелевскую премию за открытие, объяснение и использование эффекта, носящего имя Черенкова.
Как обнаружил С.И. Вавилов, — продолжил Франк, — и у Зоммерфельда был предшественник — лорд Кельвин. В 1901 году он указал на то, что атом, летящий в пустоте со сверхсветовой скоростью, должен создавать электромагнитную волну, аналогичную волнам Маха в акустике… Обсуждался и вопрос о том, как могло случиться, что высказывание Кельвина оказалось забытым… После появления теории относительности изменились представления об эфире: стало очевидным, что сверхсветовая скорость в вакууме неосуществима, и естественно, что высказывание Кельвина, так же как и работа Зоммерфельда, в какой-то степени справедливо были забыты.
Однако этого нельзя сказать об ещё более раннем и совершенно поразительном предвидении современной теории. Недавно выяснилось [Тяпкин А.А. // УФН, 1974, т. 112, с. 735], что ещё раньше в 1988 г. Хевисайд чисто умозрительно рассматривал движение точечного заряда в диэлектрике со скоростью, большей скорости волн, и получил известное соотношение, связывающее характерный угол излучения со скоростью света в среде и скоростью частицы. Вот, что писал об этом А.А. Тяпкин в 1974 г.: «Недавно, просматривая работу О. Хевисайда "Об электромагнитных эффектах при движении электризации через диэлектрик", опубликованную в 1889 г., я обнаружил в ней параграф, специально посвященный рассмотрению движения заряда q со скоростью v, превышающей скорость распространения света в диэлектрике u. В нем с самого начала автор делает следующий фундаментальный вывод: "Теперь само собой встает вопрос: какая возникнет ситуация, если v > u? Прежде всего ясно, что здесь совсем не может быть возмущения впереди движущегося заряда (точечного для простоты). Затем, учитывая, что сферические волны, излучаемые зарядом при его движении вдоль Z-оси, распространяются со скоростью u, найдем, что геометрическое место точек их фронтов есть коническая поверхность, вершина которой есть сам заряд, ее Z-ось и угол φ дается соотношением sin φ = u/v" [1, с. 13 – 15].
Очевидно, что здесь Хевисайд мысленно представил себе картинку, изображенную на рис. 4, и пришел к единственно верному заключению, к которому опытным путем пришел Мах. Позднее методологическая установка квантовой механики и теории относительности сделала совершенно невозможным для советских физиков — Черенкова, Вавилова, Тамма, Франка, Скобельцына, Гинзбурга и пр. — постановку данного вопроса в плоскости классической физики.
Рассказывая О формуле, описывающей классический эффект Доплера, мы вывели абсолютно точную и универсальную формулу Доплера, справедливую и для случая, когда v > c или β > 1:
. (4)
В формула (4) участвует только угол наблюдения θ. Но легко получить формулу, в которой фигурировал бы только угол φ между v и c:
. (5)
Разница между формулами (4) и (5) точно такая же, как между формулами (2) и (3). С точки зрения физики было бы ошибкой считать φ углом наблюдения, им является именно угол θ. Это прекрасно видно в случае, когда возникает ударная волна. На анимационном рис. 1б видно, как конус ударной волны перемещается вместе с источником колебаний. Значит, для получения формулы Маха (2) и тесно связанной с ней формулы (4) нужно перейти из неподвижной системы координат (x, y) в штрихованную систему координат (x', y'), начало которой совмещено с движущимся источником волн.
Если подкоренное выражение в формуле (4) окажется отрицательным, то корни из него будут мнимыми, что недопустимо. Условие:
1 – β2 sin2θ ≥ 0, sinθ ≤ |±1/β| или θ ≤ arcsin |±1/β|.
является ничем иным, как формулой Маха (2). Так, самым естественным образом, связываются два выражения описывающие, по сути дела, один и тот же колебательный процесс.
В связи с господством в наше время релятивистских предрассудков необходимо особо отметить, что точная формула сложения двух скоростей при угле θ = ±π/2 дает так называемый поперечный Доплер-эффект, который якобы имеет место только в теории относительности. Этот тривиальный факт очевидным образом усматривается из рис. 6. Глядя на него, релятивисты возражают, они не видят здесь поперечного эффекта.
 |
Рис. 6. Чертеж иллюстрирует тривиальный факт: при β < 1 и θ = ±90° точная формула дает поперечный Доплер-эффект
Есть формула (4), позволяющая правильно рассчитать положение концентрических (β < 1) или эксцентрических (β > 1) эквифазовых окружностей (изобар — линий максимального сжатия воздуха или любой другой среды), чего нельзя сделать с помощью формулы (1). Данная формула отвечает правильному пониманию общей картины явления, получившего название эффект Доплера. Если какие-то дефиниции, сформулированные для самого простейшего случая, не применимы к более сложной ситуации, то нужно переопределить эти дефиниции для данного случая, а не ломать правильно выстроенную картину динамики волн.
Будучи мальчишкой, мне приходилось многократно смотреть мотоциклетные гонки по льду. Я обратил внимание, что мотоцикл, мчащийся на большой скорости мимо меня, изменял высоту тона двигателя с высокого на низкий. Старший брат объяснил мне тогда, что это происходит в связи с проявлением эффекта Доплера. В самом деле, прямо передо мной мотоцикл, следовательно, угол θ, под которым я на него смотрю, прямой. Его уже нет в точке 0, откуда донеслась до меня первая волна, он находится в точке В — я это вижу — и мое ухо слышит тон, соответствующий строго регулярному расположению гребней волн на линии АВ. На линии 0А в момент восприятия звука гребни располагаются так, что об определенной длине волны здесь невозможно ничего сказать. Значит, угол А0В = φ нельзя назвать углом наблюдения или углом восприятия звуковых волн. Отсюда вывод: рис. 6 соответствует моменту проявления поперечного Доплер-эффекта.
Звуковые волны — это периодическое сжатие и разряжение воздуха. Неважно, с какой стороны волны подходят, т.е. направленность волнового вектора здесь не играет принципиальной роли (на этот вектор постоянно ссылаются мои оппоненты). Давление воздуха в единице объема величина скалярная. Значит, воздействие этого давления на мою барабанную перепонку произойдет в любом случае, откуда бы звук ни шёл — сбоку сзади, спереди — откуда угодно.
Представьте себе поплавок на поверхности воды. Мимо проплывает лодка, от которой расходятся волны. Поплавок начинает совершать поперечные колебания, аналогичные электромагнитным колебаниям. Частоту или период колебаний поплавка мы можем воочию наблюдать и легко замерить, хотя из-за непрерывного движения лодки волны к поплавку подходят с различной стороны и имеют различную форму. Однако мгновенно сделанная фотография, когда между лодкой и поплавком будет наименьшее расстояние, зафиксирует конкретную длину волны, по которой мы можем рассчитать конкретный период и частоту колебаний.
Эта фотография будет в точности отражать картину волн, изображенную на рис. 6. В соответствии с величиной скорости c' на момент, когда угол наблюдения θ = π/2, поперечная длина волны будет равна
.
Данное выражение часто встречается в теории относительности, хотя из-за парадокса штриха релятивистский радикал можно увидеть и в знаменателе. Почему так происходит?
Парадокса штриха
Дело в том, что релятивисты отказываются иметь дело с эфиром или какой-либо иной средой, заменяющей его. Они также рассматривают только относительную скорость v, которая составляется из разности двух скоростей: скорости приемника v1 и скорости источника v2. Однако, чем по сути являются скорости v1 и v2 в случае акустических волн или волн на водной глади? Ответ более чем очевиден: скорости v1 и v2 являются абсолютными скоростями наблюдателя A и источника i, движущихся в покоящейся среде, т.е. скорости v1 и v2 измеряются относительно покоящейся среды. Когда среда есть, формулы Доплера имеют определенный смысл, который тут же исчезнет, если среду убрать. Повторяем, этот простой и понятный вывод справедлив как для новой, так и для старой формулы, поэтому ошибку можно было заметить ещё до 1881 года.
Известно, если приемник покоится, а источник движется, то длина волны, согласно принятой сегодня теории, определяется выражением:
; (6)
если источник покоится, а приемник движется, будем иметь:
. (7)
Подчеркнем, здесь v1 и v2 — скорости источника и приемника относительно среды. Теперь представьте себе, что среда отсутствует, нет отдельно скорости v1 и отдельно скорости v2, но есть некая относительная скорость v = v1 – v2. У нас тут же возникнут проблема: мы не будем знать, какой из двух формул — (6) или (7) — необходимо воспользоваться. Нетрудно догадаться, что никакого критерия выбора между двумя вариантами у сторонников тотального принципа относительности не существует. Формулы (6) и (7) выводились из физики волновых процессов, протекающих именно в среде, которая и вносит в формулы некий элемент абсолютности. Можно ожидать, что в книгах по релятивистской физике числитель и знаменатель математических выражений, описывающих эффект Доплера будет произвольным образом меняться местами, что и происходит в действительности. В частности, если вы загляните в «Справочник по физике» Б. М. Яворского и А.А. Детлафа, в «Оптику» Д. В. Сивухина, «Общую физику» Ж. Росселя и в «Оптику движущихся тел» У. И. Франкфурта и А. М. Френка, то сами увидите, какую путаницу посеяли релятивисты — враги науки и друзья средневековой схоластики.
Неопределенность, о которой здесь говорится, внес Эйнштейн в своей самой первой работе 1905 года по теории относительности [4], когда решился «выбросить» из теоретической физики эфир за его якобы ненадобностью. Но если читатель хочет мыслить отчетливыми физическими представлениями, он должен помнить, что скорость света (300 000 км/с) была измерена именно относительно покоящегося эфира. Невозможно говорить вообще о некой скорости безотносительно к чему бы то ни было, поскольку Земля, Солнце и все прочие объекты непрерывно движутся. Например, если говорится, что скорость звука в воздухе равна 332 м/с, то эта скорость была измерена относительно покоящегося воздуха.
Пусть кто-нибудь попытается «отменить» воздух. Тогда вместе с ним придется «отменять» и скорость звука, иначе будет непонятно относительно какого объекта была измерена скорость 332 м/с. Поэтому там, где в формулах пишется константа с, там неявно подразумевается покоящейся эфир. И, наоборот, неотъемлемым свойством мировой среды, заполняющей вселенную, является скорость света. Если релятивисты под константой с понимают скорость распространения электромагнитной волны, которая представляет, по их заявлению, «особую форму материи», то все равно они обязаны были точно указать, относительно чего эта скорость измеряется.
В статье «К электродинамике движущихся тел» (1905) [4] Эйнштейн рассмотрел единственный частный случай, когда приемник двигался со скоростью v относительно почему-то «бесконечно удаленного источника света». Он написал формулу для воспринимаемой частоты колебаний ω' следующим образом:
,
отсюда следует выражение для λ':
(8)
где ω0 и λ0 — собственная частота и длина волны источника.
С точки зрения первого постулата об относительном движении источника и приемника, специальная оговорка о движении именно приемника колебаний выглядит нелогично. Тем не менее, эта оговорка оказалась решающей, поскольку cosθ оказался в знаменатели выражения (8). Но по теории относительности можно с равным успехом считать, что источник света движется, а наблюдатель покоится. Тогда нужно будет предыдущие формулы поставить с ног на голову:
,
отсюда следует выражение для λ':
(9)
В более поздней работе [5] Эйнштейн рассмотрел два частных случая, когда движется только приемник и отдельно когда движется только источник. При этом он написал две формулы для частоты. Логично было бы написать общую формулу, справедливую для одновременного движения с разными скоростями и приемника, и источника. Но Эйнштейн этого шага не сделал, поэтому формула вида
,
в его четырехтомном «Собрании научных трудов» отсутствует. Зато ее можно найти у других релятивистов, например, в одной из статей Макса Лауэ [2, с. 230]. Однако данное выражение позволяет уже однозначно установить, что именно движется относительно эфирной среды — приемник или источник. Таким образом, она выпадает из релятивистской концепции.
То ли сами релятивисты, то ли под действием критики своих безвестных оппонентов, только позднее ошибочная логика Эйнштейна ими была отвергнута. Вместо раздельных скоростей приемника и источника релятивисты стали брать их относительную скорость. Но принцип относительности движения приемника и источника в отсутствии эфира на формулу Доплера, как было сказано, распространить нельзя, так как тут же возникает принципиальная неопределенность в написании формул. В результате сегодня мы наблюдаем полнейшую путаницу в математических выражениях, которая получила название парадокса штриха. Примерно с одинаковой вероятностью можно встретить две противоположных формулы — либо (8), либо (9).
Эта неоднозначность штриха, естественно, перекинулась на формулы для эталонов длины и времени. Одни релятивисты считают, что изменяются собственные эталоны, другие думают, что изменения происходят относительно неподвижного наблюдателя. Причем одна часть релятивистов, считает изменение времени абсолютными (для них летающие космонавты остаются молодыми), а изменение длины стержней — относительным. Другая часть релятивистов, опираясь на другие релятивистские формулы, доказывает ровно противоположное. Одни выводят формулы изменения длины и времени из прямых преобразований Лоренца, другие — из обратных. Одни под замедлением времени понимают его укорочение (в частности, авторы учебника [6]), другие — удлинение (например, автор книги [7]). Однако поверхностное, исключительно формальное мышление релятивистов не позволяет им уловить логические разногласия в их собственном учении.
За счет произвольного местоположения релятивистского радикала мы имеем четыре варианта написания формул для изменяющихся эталонов длины и времени. Вот эти комбинации.
Эйнштейн [4, c. 18; 16, с. 419 – 420], Борн [7, с. 299 – 302] и Паули [8, с. 26 – 27] выражали изменения эталонов длины и времени следующими формулами:
( А )
,
;
в курсе теоретической физики Ландау и Лифшица [6, с. 20 – 25] эталоны изменяются однотипно:
( Б )
,
;
в Берклеевском курсе [9, с. 373 – 377] получены иные формулы:
( В )
,
;
наконец, в курсе Левича [11, с. 200 – 203] можно найти последнюю комбинацию:
( Г )
,
.
Теперь внимание! Все четыре варианта получены при одном и том же условии: штрихованная система координат движется, а нештрихованная — покоится.
На первый взгляд кажется, что авторы книг по теории относительности пишут об одном и том же. В действительности же окончательные математические выражения у них получаются взаимоисключающими. Сейчас мы можем только догадываться, почему, скажем, Ландау и Лифшиц приняли однотипный характер изменение пространственно-временных эталонов. Видимо, они понимали, что прямые и обратные преобразования Лоренца симметричны относительно радикала и не может получаться так, что при нахождении метрических масштабов в одном случае он оказывался в числителе, в другом случае в знаменателе. По диаграмме Минковского временная и пространственная оси наклонены под одним и тем же углом, поэтому и масштабные единицы должны меняться одинаково. Так что, с точки зрения математики, они были, возможно, ближе к правильному ответу. Можно понять и оправдать позицию Борна и Паули, которые писали свои книги вскоре после публикации Эйнштейна. Они хотели сделать эйнштейновские выкладки математически более прозрачными, но не решались изменить первоначальную формулу и толкование «замедления» времени.
Как бы там ни было, но нам сейчас ясно, что математика здесь играет подчиненную, чисто иллюстративную роль; она не является необходимым звеном в цепи доказательства некоего утверждения, смысл которого пришел в физику не из строгих математических формул. Создается впечатление, что все физики на словах договорились, что в движущейся системе линейка будет укорачиваться, а часы замедляться. Но они не договорились о расстановке штриха в соответствующих формулах, а также о том, откуда ведется наблюдение за объектами — из покоящихся или движущихся координат, какими преобразованиями Лоренца пользоваться при выводе формул — прямыми или обратными, что понимать под замедлением времени — его удлинение или сокращение. Поэтому в этом исключительно важном для философии релятивизма пункте происходит физико-математический сбой в формулах, который практически сводит на нет главный вывод всей современной физики.
В связи с парадоксом штриха хочется обратиться с большой и важной просьбой к нашим релятивистам: «Господа хорошие, подскажите несчастному доценту, какую книгу рекомендовать студентам для изучения азов теории относительности. Опрос студентов я провожу с помощью автомата — знаете, есть такой: из четырех предложенных комбинаций нужно выбрать единственно правильную. Вот я и гадаю, против какого варианта — А, Б, В, Г — ставить слово "да", а против каких — "нет". Очень вас прошу помочь в этом запутанном деле, а то как-то неудобно перед студентами получается. И уж позвольте мне пожалеть неокрепшие умы ребят и не вдалбливать им эйнштейновское учение до тех пор, пока славные мужи Российской Академии в лице руководства Физического института РАН не скажут всем преподавателям страны, какому варианту нужно отдать предпочтение и почему».
Но вернемся к нашим двум альтернативным выражениям для описания эффекта Доплера. Обе формулы (8) и (9), разумеется, ложны, поскольку в них лежит ошибочная логика приближённого вычисления, о чём подробно говорилось выше. Чтобы в этом убедиться самым наглядным образом, воспользуемся еще раз элементарной компьютерной программой, позволяющей по формулам строить графики в полярных координатах. На рис. 7 показана диаграмма зависимости λ' от угла θ, рассчитанная по формуле (8) при β = 3/4 (а) и β = 0,99 (б). Здесь волновой фронт уже не представляет собой кардиоиду, а всего лишь эллипс. При малой величине параметра β этот эллипс превращается в окружность, что удовлетворяет принципу Гюйгенса и результат близок к истине. Давайте разберемся, почему при малых β релятивистская формула (8) близка к классической?
 (a) (a) |
 (б) (б) |
 (в) (в) |
 (г) (г) |
Рис. 7. Форма волнового фронта, рассчитанная по формуле (8) при β = 3/4 (а), β = 0,99 (б); имеем кривые в виде эллипса. Если расситывать по формуле (9) при β = 3/4 (в), β = 1 (г), то в итоге получим кардиоиды.
До сих пор нами рассматривалось движение только источника колебаний; приемник в виде датчика или живого наблюдателя отсутствовал. Чтобы вывести общую формулу для совместного движения источника и приемника с различными скоростями, введем следующие обозначения:
,
λ0 — собственная длина волны источника колебаний,
λ1 — длина волны колеблющейся среды,
λ2 — длина волны, воспринимаемая приемником.
В этих обозначениях выражение для движущегося источника предстанет в форме:
λ1 = λ0F(β1, θ1), где β1 и θ1 — параметры источника.
Длина волны для движущегося приёмника определится формулой:
λ2 = λ1/F(β2, θ2), где β2 и θ2 — параметры приёмника.Приемник ничего «не знает» об источнике — движется он или покоится — и какова его собственная частота λ0. Он воспринимает колебание среды λ1 в конкретной точке как автономный процесс. Без наличия среды никакого эффекта Доплера наблюдаться не будет. Чтобы найти результирующую длину волны λ2 от совместного движения источника и приемника, нужно первое выражение подставить во второе, получим:
.
Если параметры источника и приёмника одинаковые (β1 = β2, θ1 = θ2), то, согласно только что выписанному выражению, воспринимаемая длина волны не будет отличаться от собственной длины волны источника (λ2 = λ0). Отсюда следует исключительно важное следствие, а именно: с помощью интерферометра Майкельсона – Морли нельзя определить движется или покоится Земля, так как его источник и приемник находятся на одной несущей платформе, движущейся со скоростью Земли.
В математике справедливы следующие приближения:
 ,
,
 ,
,
 .
.
Применяя их должным образом к выражению F(β1, θ1), можно доказать справедливость следующего приближённого равенства:
. (10)
Выражение (10) определяет уравнение эллипса в полярных координатах, что и демонстрируют графики на рис. 7 (а, б). Правда, из-за знака "+" в знаменателе, эллипс развернут в другую сторону, но в принципе получается, что точная классическая формула (4) случайно совпала с релятивистской формулой (8), когда параметр β1 мал. Поэтому для движущегося источника и покоящегося приёмника релятивисты могут себя поздравить: их теория подтверждается в эксперименте, хотя в действительности они имеют дело, конечно же, с классическим случаем.
Однако для движущегося приёмника и покоящегося источника ситуация радикально меняется и не в пользу релятивистов. При малом значении параметра β2 имеет место приближенное равенство:
. (11)
Это выражение определяет уже уравнение кардиоиды, что и подтверждают графики на рис. 7 (в, г). За счет уменьшения релятивистского радикала, для кардиоиды увеличивается значение радиус-вектора, но во всем остальном её форма остается такой же, как и для традиционной формулы (1).
Таким образом, за счет парадокса штриха вся современная физика превратилась в один огромный ком спекуляций. Кроме того, в силу приближенного равенства (10) классический эффект Доплера принимается за релятивистский. Особенно это касается ближнего и дальнего космоса и распространения электромагнитного излучения в пустом пространстве от искусственных космических аппаратов, звезд и других движущихся астрономических объектов. Все эксперименты, проведенные в лабораториях мира с движущимися источниками и малыми значениями β, которые были осуществлены с целью подтверждения теории относительности, ее более или менее "подтвердили". Косвенно эти опыты подтвердили и верность формулы (1), так как явно указывали на различие релятивистской и классической механики волн. Хотя, в действительности, существует одна и только одна формула (4) для описания динамики волн любой природы.
[1] Франк И.М. Излучение Вавилова – Черенкова. Вопросы теории. – М.: Наука, 1988.
[2] Лауэ М. Статьи и речи. – М.: Наука, 1969.
[3] Черенков П.А. Излучение частиц сверхсветовой скорости и некоторые применения этого излучения в экспериментальной физике (Нобелевская лекция). /УФН, 1959, т. 68, #3, с. 378–386.
[4] Эйнштейн А. К электродинамике движущихся тел. СНТ. Т.1. – М.: Наука, 1965.
[5] Эйнштейн А. Теория относительности. СНТ. Т.1. – М.: Наука, 1965.
[6] Ландау Д.Д. и Лифшиц Е.М. Теория поля. – М., 1973.
[7] Борн М. Эйнштейновская теория относительности. – М., 1964.
[8] Паули В. Теория относительности. – М., 1947.
[9] Механика. БКФ. Т.1. Ч. Киттель, У. Найт, М. Рудерман. – М., 1971.
[10] Франкфурт У.И., Френк А.М. Оптика движущихся тел. – М.: Наука, 1972
[11] Левич В.Г. Курс теоретической физики. Т.1. – М.: Физматгиз, 1962.