
Квантовая теория Доплер-эффекта В.Л. Гинзбурга
Олег Акимов
Когда аспирант П.А. Черенков и его руководитель академик С.И. Вавилов обнаружили в 1934 году световой конус ударной волны, вызванный электронами, движущимися в прозрачной среде со скоростью больше скорости света в этой среде, у ортодоксальных релятивистов возникли серьезные проблемы. В книге «Излучение Вавилова – Черенкова. Вопросы теории» И.М. Франк писал: «Были рассмотрены различные гипотезы, о которых теперь уже невозможно вспомнить, и все они оказались бесплодными. Выяснилось, что наглядная картина, использующая принцип Гюйгенса, — это единственная, дающая качественно правильный результат. И величина β = v/u, и пробег наиболее энергичных комптоновских электронов действительно могли дать требуемую направленность волн под острым углом к скорости электрона» [1, с. 31].
Тем не менее, Франк и его коллеги пошли по пути квантовой физики. Особенно усердствовал в этом направлении лауреат Нобелевской премии за 2003 год. Франк пишет: «Что касается теории, то первое развитие теории получила в работах В.Л. Гинзбурга, давшего квантовое рассмотрение явления и распространившего теорию на случай оптически анизотропной среды (1940 г.).» [1, с. 34 – 35].
Итак, в 1940 году эффект Вавилова – Черенкова в голове В.Л. Гинзбурга превратился из волнового процесса, тесно связанного с принципом Гюйгенса, в квантовый, при котором нужно было оперировать фотонами, т.е. корпускулярными представлениями. Давайте посмотрим, какое теоретическое здание тогда еще молодой и только-только начинающий теоретик возвел на обыкновенном оптическом явлении, с которым неожиданно столкнулся аспирант Черенков, работавший в начале 1930-х годов по заданию Вавилова над темой люминесценции. В этом деле нам поможет доклад Гинзбурга, прочитанный в 1996 году по случаю получения им Большой золотой медали имени Ломоносова.
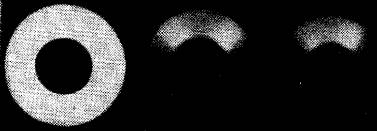 (a) (a) |
 (б) (б) |
Рис. 1 (а) Фотографии углового распределения интенсивности излучения: обычная люминесценция (снимок слева), свечение этилциннамата (n = 1,58043, снимок в центре), свечение воды (n = 1,3371, снимок справа). (б) Угловые распределения интенсивности для этилциннамата: верхняя кривая соответствует возбуждению свечения комптоновскими электронами от лучей ThC (β = 0,866), нижняя — от Ra (β = 0,866).
Перед цитированием Гинзбурга с целью большего удобства приведем четыре наиважнейшие для нас формулы из предыдущего раздела:
традиционная формула для Доплер-эффекта —
, (1)
формула Маха для акустического конуса —
sin θ = 1/β = c/v, (2)
формула Черенкова для оптического конуса —
cos φ = 1/nβ, φ = arccos (1/nβ), (3)
уточненная формула для Доплер-эффекта —
. (4)
Здесь предполагается, что источник света движется, а его приемник покоится, при этом β = v/c — скорость движения источника относительно скорости распространения колебаний, φ — угол между векторами v и c, θ — угол наблюдения, λ и λ' — собственная и принятая длина волны. Если v > c или β > 1, то появляется конус ударной волны, показанный на рис. 2.
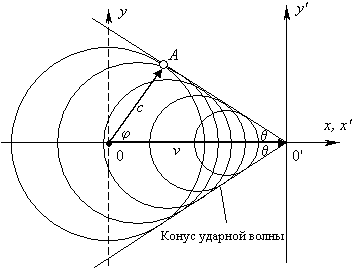 |
Рис. 2. Чертеж, позволяющий получить формулу (2) для определения угла θ при вершине конуса ударной волны
«Как на квантовом языке, — задается вопросом Гинзбург, — объяснить отсутствие в вакууме излучения равномерно движущегося заряда (или другого источника, не имеющего собственной частоты)? Для этой цели достаточно использовать законы сохранения энергии и импульса при излучении фотона частицей:
Далее Гинзбург замечает: «Легко убедиться в том, что» данная система уравнений при β < 1 не имеет решения, «т.е. излучение невозможно» » [2, с. 1037]; «излучение возможно (т.е. cos θ < 1 и ω > 0) только при сверхсветовом движении» [4, с. 541]. Это вытекает из анализа аналогичных уравнений сохранения для среды, решение которых дается двумя равенствами:
Первое равенство при условии
переходит в
,
что является известным условием излучения Вавилова – Черенкова. Однако указанное условие равносильно условию классичности ситуации, когда постоянная Планка устремляется к нулю. Тогда о каких квантах здесь можно говорить? В связи с этим казусом Гинзбург напускает дымовую завесу: «В условиях, когда результат не содержит постоянную Планка, квантовый расчет имеет лишь методическое значение» [4, с. 541]. Если откровенно сказать, никакого значения. С возрастом этот фиговый лист Гинзбург отбросил и честно признался: «В этой связи Л.Д. Ландау в 1940 г., когда ему рассказали о моей работе, заметил, что она не представляет интереса. Как ясно из сказанного, для такого заключения у него были основания, и это вообще характерно для критических замечаний Ландау — обычно они били в цель» [2, с. 1037].
Что сделал Гинзбург с точки зрения математики? Мы видим, что ему нужен был «чистенький» косинус без всякого там квантово-релятивистского довеска. Для этого он и освободился от второго члена в квадратных скобках путем непосредственной «ампутации» математического выражения. Употребленный здесь термин взят из стародавней статьи бывшего директора ФИАНа, Д.В. Скобельцына, которого страшно возмутила манера Гинзбурга обращаться с формулами. Статья называется «Парадоксы квантовой теории эффектов Вавилова – Черенкова и Доплера», в которой автор камня на камне не оставил от статьи В.Л. Гинзбурга и В.А. Угарова, написанной годом раньше. Скобельцын пишет: «Если вместо (3.22) в интеграл (3.9) поставить "ампутированное", как указанное выше, выражение (4.1) и провести все вычисления» [5, с. 312], то авторы всегда получат, что они хотят. В этом и состоит суть формально-феноменологического метода, о котором беспрестанно говорит Гинзбург. Его идея такова: имеется феномен (в данном случае эксперимент Вавилова – Черенкова); нужно путем формальных манипуляций под этот феномен подогнать конкретную теорию, опирающаяся на супергибкую квантовую механику и теорию относительности.
Не хочется вдаваться в содержание статьи Скобельцына и выяснять, что подразумевается под (3.22), (3.9) и (4.1) — это сильно нас отвлечет, — но одно место для внесения большей ясности в нашу проблематику необходимо всё же процитировать.
…Свободный электрон, движущийся прямолинейно и равномерно в пустом пространстве, — пишет критик Гинзбурга, — не может излучить свет за счет своей кинетической энергии. Опираясь на основы теории относительности, к такому заключению можно прийти сразу же, если ввести инерциальную систему отсчета, в которой рассматриваемый электрон покоится и в которой, следовательно, энергия, необходимая для излучения фотона при заданных условиях, равна нулю. Однако, как хорошо известно, электрон в состоянии равномерного движения в среде дает такое излучение — излучение Вавилова — Черенкова.
Если воспользоваться указанной выше системой отсчета (в которой электрон неподвижен), то возникает вопрос — где же источник энергии черенковского излучения? На этот вопрос естественно ответить предположением, что таким источником является кинетическая энергия движения среды, взаимодействующей с э.-м. полем покоящегося в ней электрического заряда.
Такой ответ не вызывает сомнений при "глобальной" — макроскопической — постановке вопроса. Однако схема трактовки микроскопической — квантовой картины явления приводит к другому ответу на поставленный выше вопрос. В основу квантового описания положены соотношения, вытекающие из тензора Минковского, и следующее парадоксальное их следствие.
В указанной системе отсчета (в которой электрон покоится), внутри "конуса излучения Черенкова" энергия, фотона отрицательна: фотон, испускаемый в этих условиях, не уносит, а наоборот, отдает энергию (а также и импульс) излучающему его электрону. Тем самым, как нами уже и отмечено, обнаруживается прямое противоречие с фундаментальным соотношением Эйнштейна E = mc². В дальнейшем мы подробно обсудим возникающую таким образом контроверзу [5, с. 296].
Претензия Скобельцына к Гинзбургу и Угарову как раз и состояла в том, «что полученный авторами удовлетворяющий их результат достигается за счет нарушения тех общих принципов релятивистской механики, которым подчинен выбор выражения силы (или плотности силы) в движущейся среде» [5, с. 313]. Еще раньше в 1947 году Гинзбург кооперировался с Франком для написания статьи на тему квантовой интерпретации эффекта Черенкова. Однако основной мишенью Скобельцына был, в основном, один Гинзбург, поскольку именно он первый в 1940 году начал насильственно внедрять в классическое явление оптики спекулятивные элементы квантовой механики. Поэтому нижеприведенный отрывок главным образом адресуется ему.
Теория, из которой вытекает квантовая формула эффекта Комптона, — берет для сравнения Скобельцын, — обладает престижем, основанным на таком множестве экспериментальных подтверждений, которое в настоящее время едва ли обозримо. Что ж касается квантовой теории черенков-эффекта, то в активе этой теории вообще нет каких-либо экспериментальных подтверждений, а в пассиве ее — противоречия кардинальным требованиям релятивистской механики.
В основу квантовой модели черенков-эффекта положено представление о переходе электрона из одного состояния прямолинейного движения в другое его состояние, с сопутствующим этому переходу излучением. Невозможно представить себе конкретную обстановку эксперимента, в которой можно было бы, хотя бы в принципе, обнаружить такого рода переходы. Образам, использованным в квантовой модели черенков-эффекта, нельзя приписать прямой физический смысл. С другой стороны, в результате многолетних экспериментов можно уверенно утверждать, что корпускулярные образы являются адекватной формой интерпретации эффекта Комптона. Имеется обоснованная уверенность в том, что в этом случае любые следствия корпускулярной модели, в принципе, могут быть прямо подтверждены экспериментом.
Подводя итоговую черту, можно констатировать, что попытки квантовой трактовки рассмотренных выше эффектов на основе простых квазиклассических моделей не приводят к удовлетворительным результатам.
В сущности, это и следовало ожидать заранее.
Во-первых, модель, о которой шла речь (в гл. 3 и 4 статьи), представляется сверхупрощенной и, во-вторых, едва ли вообще, оставаясь в рамках классических представлений, можно описать квантовый механизм излучения [5, с. 316].
Итак, «квантовая» теория, созданная Гинзбургом в 1940 году была раскритикована Ландау. Гора родила мышь: громоздкие квантово-релятивистские уравнения давали простенькую формулу для конуса ударной волны, только в условиях классической физики. Достигалось же это путем грубой «ампутации» квантово-релятивистского члена в формуле для косинуса. Зачем Гинзбург при чтении церемониального доклада 1996 года напомнил о промахах своей молодости, не понятно. Однако Скобельцын, как мы видим, критикует совсем другой вариант квантовой теории Гинзбурга, к которому мы сейчас и переходим.
Позднее зрелый теоретик Гинзбург напрочь забывает про электроны, фигурирующие в эксперименте Черенкова, поскольку они «не имеют собственной частоты», и берется рассматривать атомы или молекулы, которые излучать в принципе могут. «Если такой источник движется в вакууме с постоянной скоростью v (в лабораторной системе отсчета), — говорит Гинзбург, — то в этой лабораторной системе частота излучаемых волн равна
где θ — угол между волновым вектором k (направлением наблюдения) и v. Частота ω0 — это частота колебаний в лабораторной системе» [2, с. 1037].
Естественно, мы находимся в лаборатории. И что же получается? Чтобы в релятивистской формуле избавиться от нежелательного для нас сейчас радикала, нужно просто распахнуть дверь в мысленную лабораторию и мысленно войти в нее? Как видим, перед нами всё тот же славный хирургический метод «ампутации» ненужных нам членов в математическом выражении.
Далее Гинзбург переходит к среде с показателем преломления n(ω) и коренным образом меняет предыдущую формулу:
сообщив при этом, что «под корнем
замену c на c/n делать не нужно, так как этот корень связан с замедлением времени для движущегося источника и не имеет отношения к процессу излучения» [2, с. 1037]. Это, конечно, тоже вольность, но релятивистам невозможно доказать, что все формулы физики должны записываться, исходя из данной конкретной ситуации, а не из каких-то общих принципов. Если в данном эксперименте не зафиксировано замедление времени, то нечего о нем и говорить. Но это так, мелочи; главная методологическая ошибка здесь заключается в другом.
Обратите внимание, в последней формуле наряду с показателем преломления n(ω) появляется модуль. Зачем он понадобился Гинзбургу? Ясно зачем: ведь если v > c, то ω(θ) < 0, а отрицательных частот в природе не бывает. Вот наш теоретик и решил волюнтаристским приёмом исключить этот нежелательный для него и природы результат. Незадачливый хирург «пришил» к формуле необходимые ей две черты, совершенно не понимая, что тем самым он не просто исключил отрицательные частоты, но и в корне изменил поведение функции ω(θ).
Однако данный подгоночный прием не решает главную задачу, а именно: когда βn > 1 появляется излучение Вавилова—Черенкова теперь уже, по воле Гинзбурга, с положительной частотой ω(θ) > 0. Но при βn < 1 Черенков не наблюдал никакого излучения. Как с этим-то быть? Очень ответственный для нас момент; собственно, с него начинается Великая Квантовая Теория Гинзбурга.
Прежде всего автор ее делит эффект Доплера на нормальный и аномальный, как показано на рис. 3.
.
Рис. 3. Область нормального (θ > θ0) и аномального (θ < θ0) эффекта Доплера по версии В.Л. Гинзбурга.
Обращаясь к последней выписанной здесь формуле, Гинзбург говорит, что по ней полезного для нас «ничего сказать нельзя и отличие между нормальным и аномальным эффектами Доплера не представляется особенно существенным. И вот оказалось, что квантовый подход (или, точнее, использование законов сохранения энергии и импульса) позволяет вскрыть очень важную особенность аномального эффекта Доплера. Будем считать, что излучатель представляет "систему" (атом) с двумя уровнями — нижним уровнем 0 и верхним уровнем 1 (рис. 4)
.
Рис. 4. Переходы между атомными уровнями 0 и 1 в случае нормального (а) и аномального (б) эффекта Доплера, согласно квантовой теории В.Л. Гинзбурга.
Тогда при использовании законов сохранения [выше они уже приводились] нужно лишь изменить выражение для энергии излучателя, учитывая наличие внутренних степеней свободы (уровней). Это значит, что энергия
где
— полная энергия системы (атома) в нижнем состоянии 0, а
— та же энергия в верхнем состоянии 1. Энергия W1 > W0 и покоящийся атом при переходе 1 → 0 излучает частоту
».
Далее выясняется, что
"в области нормального эффекта Доплера атом, как и в вакууме, переходит с верхнего уровня 1 на нижний уровень 0… В области же аномального эффекта Доплера, напротив, при излучении фотона происходит возбуждение атома — он переходит с уровня 0 на уровень 1 (см. рис.14). Энергия при этом черпается из кинетической энергии поступательного движения… При этом оказывается, что излучение волн в области вне черенковского конуса (т.е. при нормальном эффекте Доплера) тормозит колебания. Напротив, излучение, идущее внутрь черенковского конуса, отвечающее аномальному эффекту Доплера, раскачивает колебания осциллятора, т.е. возбуждает его" [2, с. 1038].
Скобельцын был, конечно, прав: всё в этой теории выглядит надуманно. Ничего подобного Черенков не наблюдал и все гинзбурговские придумки с уровнями проверить невозможно. Но предположим, что внутри атомов и молекул существуют два уровня 0 и 1, на которые «спрыгивает» электрон, однако в равномерно движущемся электроне таких уровней нет — там-то что «прыгает»? Но вновь пойдем навстречу автору и забудем про электроны, целиком сосредоточимся на фотонах. По теории Гинзбурга, излучение фотонов в атоме происходит как при нормальном эффекте Доплера, так и при аномальном; отличие заключается лишь в степени вероятности. Однако никто не отменял релятивистское положение о том, что равномерно и прямолинейно движущийся заряд при βn < 1 не испускает никаких волн или фотонов. Зачем, спрашивается, нужно было городить весь этот огород из формул, если он не дает наблюдаемого в опыте результата? Здесь мы сталкиваемся с той странной манерой творчества Гинзбурга, когда все его теоретические построения ничем не заканчиваются.
Противоречие нормального эффекта Доплера, представляется очень любопытным. В более ранней и более детально прописанной работе, изобилующей формулами, Гинзбург выражается столь же неопределенно, что и в докладе 1996 года. В 1959 году он написал:
«Если система [атом или молекула] имеет только два дискретных уровня 0 и 1, то при βn < 1 (досветовое движение) в стационарном состоянии излучатель [атом] находится на нижнем уровне 0… если возбужден уровень 1, то через некоторое время система высветится с переходом на уровень 0. Если же βn > 1 (сверхсветовое движение), то и в стационарных условиях имеется вероятность найти систему на уровне 1 и она все время излучает как нормальные, так и аномальные доплеровские волны… интенсивность излучения нормальных и аномальных волн определяется, очевидно, отношением суммарных вероятностей излучения этих волн» [3, с. 542]. «Далее, ясно, что при сверхсветовом движении потоков систем с двумя или многими уровнями, как правило, должно иметь место не поглощение (реабсорбция), а усиление (отрицательное поглощение) аномальных доплеровских волн» [3, с. 543]. «…при наличии аномального эффекта Доплера (т.е. если βn > 1) пучок частиц, находящихся на одном только нижнем уровне 0, обладает отрицательным поглощением [положительным испусканием], и излучаемые отдельными частицами волны усиливаются. Это обстоятельство является, по-видимому, весьма благоприятным с точки зрения возможности использования пучков частиц, движущихся в диэлектрической щели или замедляющей системе, для генерации и усиления микроволн» [3, с. 543—544].
За этим наукообразными словесами просматривается желание Гинзбурга представить дело так, будто степень вероятности излучения фотона при нормальном эффекте Доплера столь незначительна, что ее не стоит и принимать во внимание. Релятивиста Скобельцына данная проблема, похоже, не заинтересовала. Он больше обеспокоился тем, что квантовая теория Гинзбурга противоречит догмам спекулятивной физики. Статью 1977 года он заканчивает так:
Таким образом, в результате введения некоторой произвольной гипотезы удается установить подобие схемы описания рассматриваемых эффектов картине, вытекающей из квантовой теории этих явлений. Квантовым языком, использующим концепцию "псевдоимпульса" фотона, оказывается возможным пользоваться для приближенного описания известных закономерностей черенков-эффекта. Корпускулярные представления приводят к формуле (приближенной) допплер-эффекта, которая соответствует требованиям кинематики.
Вместе с тем согласование представлений о квантовом фотоне с теорией относительности оплачивается ценой отказа от некоторых фундаментальных квантовых соотношений. Уравнение Планка — Эйнштейна E' = hν' в движущихся средах не выполняется (здесь E' — энергия цуга волн, заданная уравнением E0 = hν0, где E0 и ν0 — значения энергии и частоты данного цуга в среде неподвижной).
Что же касается обоснованности предсказаний специфически квантовых эффектов таких, как самовозбуждение атома, высвечивающегося при излучении света внутри конуса Черенкова, то не следует упускать из виду, что в основу нового варианта теории положены произвольные допущения. Можно усмотреть и определенное противоречие этих допущений исходным посылкам теории.
Квантовая теория заимствует готовый аппарат квантования поля в вакууме и применяет его к среде, пренебрегая силами Абрагама и исходя из того, "что взаимодействие со средой учитывается тем, что положено ε ≠ 1".
Такая трактовка была правомерна в рамках концепций Минковского. Однако в настоящее время возникла необходимость такой переформулировки теории, в которой существенная роль должна быть отведена процессам передачи среде импульса излучения (при среде неподвижной), а также и энергии — среде движущейся… В связи с этим сама постановка задачи квантования должна быть, видимо, пересмотрена. Среда должна, по-видимому, рассматриваться как составная часть квантуемой системы. На данном же этапе квантовой теории эффектов Вавилова — Черенкова и Допплера можно приписывать лишь эвристическое значение [5, 319].
Итак, еще раз проследим за ходом мысли Гинзбурга. С самого начала он усмотрел связь между косинусом, фигурирующим в формуле (3), и косинусом, фигурирующим в формуле Доплера (1). Теоретик всеми способами пытался провести логическую цепочку от (1) к (3). Но такой связи не существует: формула (1) ошибочна, а формулу (3) правильнее писать через синус, как формулу (2). В этом случае обнаружится совершенно новая связь между синусом формулы (2) и синусом, стоящим в подкоренном выражении (4). Такая связь будет уже истинной, поскольку диктуется она не случайным сходством символов (в данном случае, символа sin θ), а безупречной логикой пространственных представлений (рис. 4 и 6). Гинзбург же отказывается от геометрических образов, а весь свой мысленный процесс строит вокруг символов (в его случае, cos θ). Далее он пытается незаконными математическими средствами доказать справедливость первоначально привидевшейся ему формальной связи между косинусами.
Разбирать альтернативную теорию, предложенную релятивистом Скобельцыным, мы не станем. Вместо этого обратим внимание на одно интересное место в докладе Гинзбурга. В 1996 году он говорил:
В 1940 г. Л.И. Мандельштам, выступая в качестве оппонента на защите докторской диссертации П.А. Черенкова, отметил, что эффект В.Ч. будет наблюдаться и в том случае, если заряд (источник) движется не в сплошной среде, а в проделанном в ней тонком пустом канале. Физически дело в том, что излучение В.Ч. формируется не только на самой траектории заряда, но и вблизи нее на расстоянии порядка длины волны излучаемого света… В качественном отношении такая же картина наблюдается при замене канала щелью или просто при движении заряда вблизи среды (диэлектрика). Все это важно в связи с тем, что при движении заряда в среде потери его энергии на излучение В.Ч. сравнительно невелики; основными являются ионизационные потери, локализованные в непосредственной близости от траектории. Поэтому при движении в каналах, щелях и вблизи среды ионизационные потери исключаются, а излучение В.Ч. сохраняется. Если для зарядов этот момент, хотя и важен, но не является решающим, то при наблюдении Доплер-эффекта в среде, когда речь идет о движении возбужденных атомов, всё явление может наблюдаться только с использованием каналов или щелей — иначе атом разрушается. Правда, Доплер-эффект может наблюдаться и наблюдается и при движении в весьма разряженной среде, в частности, в плазме [2, с. 1035].
В статье 1959 года имеется обширный параграф, который называется «Черенковское излучение дипольных моментов в сплошной среде и при движении в каналах и щелях». В нем автор рассказывает о специально разработанном им методе, содержание которого, однако, нет надобности раскрывать. Достаточно привести несколько вступительных фраз, чтобы понять ошибочность постановки задачи. Вот эти фразы:
Обычно рассматривается только черенковское излучение точечных зарядов или заряженных сгустков (пакетов). В то же время, конечно, совершенно ясно, что черенковское излучение должно испускаться любым излучателем, движущимся со скоростью v, большей фазовой скорости света в среде c/n. Другими словами, условие излучения сохраняется и для любого мультиполя, в частности для электрического и магнитного дипольных моментов; интенсивность же излучения существенно изменяется уже для диполей (не говоря уже о более высоких мультиполях) обычно значительно меньше, чем для заряда… Для элементарных частиц (электрон, нейтрон и т. д.) или атомных ядер магнитодипольное черенковское излучение очень слабо и не представляет интереса. Положение меняется, когда рассматриваются сгустки частиц, в определенных условиях излучающие подобно точечным частицам с зарядом и мультипольными моментами, отвечающими всему сгустку… Рассмотрим точечную частицу с зарядом е, электрическим дипольным моментом р и магнитным моментом m, движущуюся со скоростью v [4, с. 557–558].
В этих первых предложениях курсивом выделено слово точечный, т.е. Гинзбург принимает, что электрон не имеет протяженности, а молекула или отдельный атом снабжены электрическими и магнитными моментами. Поскольку электрон, а тем более атом или молекула, не являются точечными объектами, то вся физика явления представлена автором не верно. Заканчивается указанный параграф, а вместе с ним и статья, следующими словами:
Таким образом, справедливость формул (47)—(49) для черенковского излучения точечных диполей в сплошной среде, на наш взгляд, не вызывает сомнений. Выше можно было убедиться в высокой эффективности метода, основанного на использовании теоремы взаимности, при вычислении черенковского излучения в узких каналах. Этот метод использовался и при рассмотрении переходного излучения; он должен быть также полезен при решении целого ряда других задач теории черенковского и переходного излучения при наличии границ [4, с. 563].
.
Рис. 5. Чертеж из статьи Гинзбурга [4], в которой рассматривается теория движения точечных зарядов вдоль канала или щели.
Взгляните на рис. 5, взятый из статьи Гинзбурга [4]. Автор почему-то не озаботился вопросом, почему точечный заряд, в частности, электрон, испускает ударную волну, двигаясь, по сути, в пустом канале или щели, хотя и вблизи вещества, характеризующегося показателем преломления n. Один этот факт опрокидывает все формальные построения Гинзбурга, поскольку понятно, что электрон, атом или молекулу ни в коем случае нельзя рассматривать как точечные объекты, иначе будет совершенно непонятно, как точечный объект, двигаясь вне среды, умудряется испускать ударные волны, наклон которых определяется показателем преломления среды.
Электрон — не точка!
8 марта 1928 года, Дж. Дж. Томсон в докладе под названием «За пределами электрона» сказал буквально следующее: «…движущийся (в частности, равномерно) электрон всегда сопровождается цугом волн. Эти волны как бы несут его с собой и определяют его путь. Таким образом, движущийся электрон представляет собой значительно более сложную вещь, чем простой точечный заряд» [9, c. 571–572]. Этот вывод Томсон сделал после проведенных его сыном, профессором Г.Ф. Томсоном, экспериментов по прохождению электронов сквозь сверхтонкую фольгу. Сын сделал снимки (рис. 6), однозначно доказывающие волновую природу электронов. Копенгагенская же школа спекулятивной физики провозгласила следующую дуалистическую догму: электроны представляют собой точечные частицы; по прохождению электронного пучка через фольгу возникает волновая картина случайного распределения точечных объектов. Таким путем в их уме происходит согласование корпускулярной и волновой природы электрона.
.
Рис. 6. Снимок Г.Ф. Томсона пучка электронов, прошедшего через сверхтонкую фольгу. Дж. Дж. Томсон по поводу результата, полученного его сыном, сказал: «На рисунке виден ряд колец, положение которых в точности совпадает с положением дифракционных колец света определенной длины волны, которые бы получились при его прохождении через эту же пластинку… Согласно измерениям Г. Ф. Томсона, электронам, движущимся со скоростью в 1010 см/с, соответствует длина волны, близкая к 7,8 · 10–10 см»
Между тем сам открыватель электрона и его корпускулярно-волнового дуализма, Дж. Дж. Томсон, мыслил абсолютно по-другому. Он разработал модель электрона в виде волнового пакета, который складывается из несущих его волн. Пакет этот обладает собственными периодами колебаний, принимающими определенные квантовые значения, так как между колебаниями пакета и колебаниями несущих его волн должны возникать резонансные отношения.
«Отсюда следует, — говорит Дж. Дж. Томсон, — что импульс и энергия электрона, подобно его частотам и длинам волн, не могут принимать любых значений. Возможные значения, например, импульса, всегда отделены друг от друга конечными интервалами, так что рост количества движения идет не непрерывно, а скачками. Таким образом, мы приходим к своего рода квантованию количества движения. С нашей точки зрения, квантование является следствием и выражением определенной структуры электрона — только такие движения возможны, или, по крайней мере, устойчивы, которые находятся в резонансе с внутриэлектронными колебаниями» [9, c. 587]. «Интересно отметить, — продолжает Дж. Дж. Томсон, — что при таком взгляде на электрон применение методов классической механики ведет к результатам, которые раньше считались исключительной особенностью квантовой механики» [9, c. 589].
Последняя фраза взята из самой концовки статьи. Поскольку Гинзбург, его последователи и большинство поклонников спекулятивной физики не знакомы с конструктивным взглядом Дж. Дж. Томсона на строение основного элемента мироздания, каковым является электрон, нам не помешает познакомиться с текстом его доклада «За пределами электрона» более детально.
Подобно тому, — говорит докладчик, — как понятия световых частиц оказалось недостаточно для объяснения свойств света и пришлось ввести понятие световых волн, так и понятия электрических частиц оказалось недостаточно для объяснения свойств электронов и пришлось предположить, что эти частицы сопровождаются системами волн. Дуализм волны-частицы имеет, таким образом, место в самых разнообразных областях физики и, по-видимому, коренится в самой природе вещей. Для того чтоб оценить важность этого факта, рассмотрим вкратце, каким образом энергия переходит из одного места в другое.
Пусть, например, электрон меняет свое местоположение — возникает вопрос: каким путем следует за ним его энергия? Этот вопрос можно сформулировать яснее, если вернуться к старому представлению об электроне, как о шарике с радиусом в 10 –13 см. Когда этот шарик движется, то сосредоточена ли его энергия внутри него или она распространена по всему внешнему пространству и пролагает себе путь через эфир? Если, как я это делаю, считать, вслед за Фарадеем и Клерком Максвеллом, что свойства заряженных тел обусловливаются линиями сил в окружающем их эфире, то энергию электрона нужно представлять себе сосредоточенной не в маленькой сфере, символизирующей электрон, а во всем внешнем пространстве. Согласно этому воззрению, вся энергия сосредоточена в эфире и распространяется с одного места на другое через посредство эфирных волн.
Факт передачи энергии через эфир был впервые ясно и отчетливо сформулирован моим старым другом проф. Джоном Генри Пойнтингом. Его рассуждения приводят к результатам на первый взгляд несколько странным, хотя я считаю их, безусловно, правильными. Например, я убежден, что большинство из всех считает, что энергия электрических лампочек сообщается им от электростанции через соединяющие их медные проволоки. Согласно Пойнтингу дело обстоит вовсе не так, и энергия распространяется не по проволоке, а по окружающему ее внешнему пространству. Роль проволоки заключается не в том, что она переносит энергию, а скорее в том, что она направляет ее путь во внешнем пространстве. Энергия распространяется в виде волн по эфиру вне проволоки со скоростью, не зависящей от размеров проволоки и от ее материала [9, c. 574 – 575].
Далее Дж. Дж. Томсон рассказывает о групповой скорости, с которой передается энергия и заключает, что
эфир, который сам по себе может переносить энергию только со скоростью света, вследствие присутствия электрических зарядов переходит в сверхдиспергирующее состояние и становится способным служить передатчиком энергии с любой скоростью, меньшей скорости света. При своем передвижении энергия сопровождается цугом волн, определяющих направление ее движения, которые сами по себе, вне тех мест, где находится переносимая ими энергия, обладают лишь небольшой энергией. При этом каждой скорости передвижения энергии соответствует определенная длина волны, которая тем меньше, чем быстрее движется энергия. Скорость самих волн значительно больше скорости энергии, причем произведение этих двух величин равно квадрату скорости распространения волн через чистый недиспергирующий эфир. [9, c. 580 – 581].Дж. Дж. Томсон напоминает, что диаметр электрона (10 –13 см) был вычислен косвенно и приводит формулу, по которой велся расчет. В его модели плотный волновой пакет окружен сверхдиспергирующей областью, по своим качествам напоминающую ионосферу. Величиной этой области как раз и нужно характеризовать объем электрона, как волнового объекта.Эту величину можно хотя бы приблизительно определить из непосредственных опытов, подобных опытам Г. Ф. Томсона над получением дифракционных колец при прохождении электронов через тонкие металлические листки. Зная радиусы этих колец, можно определить длину волны электронных волн, находящихся в пределах сверхдиспергирующей области, интерференция которых и обусловливает появление колец. Для того, чтоб интерференция была заметной, электронный цуг должен заключать в себе, по крайней мере, несколько таких волн.Согласно измерениям Г. Ф. Томсона, электронам, движущимся со скоростью в 1010 см/с, соответствует длина волны, близкая к 7,8 · 10–10 см. Следовательно, диаметр сверхдиспергирующей области должен равняться самое меньшее 10–9 см, т.е. иметь значение значительно большее, чем 10–13 см, которые даются обычной теорией.
Употребляя менее быстрые электроны, можно получить большие длины волн; при этом, однако, когда длина волны станет больше диаметра сверхдиспергирующей области интерференционная картина должна будет сделаться размытой. Опыт показал, что резкие очертания у колец пропадают только тогда, когда скорость электронов делается значительно меньше, чем 1010 см/с, а длина волны значительно больше, чем 10–9 см. Возможно, однако, что на это размывание интерференции влияют и побочные причины.
Хорошо очерченные кольца получаются при длинах волн в 10–9 см следовательно, диаметр сверхдиспергирующей области во всяком случае не меньше этой величины. Этот факт вполне может быть согласован со свойствами электрона, так как нельзя забывать, что частота электронных волн весьма велика и что диспергирующая способность электрона проявляется только по отношению к очень быстрым колебаниям. По отношению же к более низким частотам, сверхдиспергирующая область может вести себя как нормальный эфир и, следовательно, не быть обнаруженной. Таким образом, вовсе неудивительно, что изучение электронных волн дает для размеров электрона более высокое значение, чем другие методы [9, c. 584 – 585].
Этих фрагментов, по-видимому, достаточного для первого знакомства с докладом Дж. Дж. Томсона. Кто желает, может прочесть полный текст доклада За пределами электрона, который размещен на нашем сайте. Правда, для ознакомления с математическими добавлениями А и В, придется обратиться непосредственно к источнику [9].
(a)
(б)
Рис. 7. Магнитные силовые линии магнита (а), благодаря притяжению железных опилок, становятся хорошо видимыми. Считалось, что электрические линии зарядов (б) обладают аналогичной системой упругих линий, хотя они и не могут быть так просто увидены. Однако эксперименты с электронами показали, что самый элементарный заряд, каковым является электрон, устроен иначе и не представляет собой крохотный шарик, от которого отходят «фарадеевские трубки». Оба рисунка взяты из книги Дж. Дж. Томсона [10]
К волновым представлениям, изложенным в докладе 1928 года, Дж. Дж. Томсон пришел не сразу. Вначале он, как Фарадей и Максвелл, считал, что электрон представляет собой заряженную сферу, от которой отходят электрические силовые линии. Такое модельное представление возникло у физиков под влиянием виденной всеми картинки распределения магнитных силовых линий (рис. 7а). По аналогии с магнитными полюсами электрическим зарядам приписывались те же геометрические свойства (рис. 7б). Однако такой взгляд на электрон был ошибочным. После эксперимента по дифракции электронов на тонкой фольге, впервые проведенного Г.П. Томсоном, Дж. Дж. Томсон изменил свои модельные представления, причем самым радикальным образом. С его представлениями об электроне сторонники установившейся к середине XX столетия спекулятивной науки уже не согласились. До сих пор в учебниках, говоря о самых элементарных зарядах, авторы изображают картинки типа рис. 7б, отражающие модельные представления физиков-классиков конца XIX века. После прихода релятивистов конструктивная наука остановилась, хотя любому исследователю нерелятивисткой ориентации понятно, что прогресс физической науки целиком связан с изменением модельных представлений. Не только Дж. Дж. Томсон, но и Максвелл, и Фарадей многократно меняли свои представления о течении электромагнитных процессов.
В 1881 году Дж. Дж. Томсон опубликовал статью «Об электрических и магнитных эффектах, произведенных движением наэлектризованных тел», которая произвела революцию в физике. В ней он доказывал, что инерционные свойства материи можно и нужно объяснять с электромагнитной точки зрения; нет массы иной природы, помимо электромагнитной. Кроме того, задолго до экспериментов Кауфмана он предсказал, что при движении с всёвозрастающей скоростью наэлектризованное тело будет вести себя так, как если бы его масса увеличивалась. Это должно происходить по тем же причинам, по которым растет сопротивление со стороны идеальной жидкости, сквозь которую движется тело. «Другими словами, — писал Дж. Дж. Томсон, — оно [сопротивление] должно быть эквивалентным увеличению массы движущейся заряженной сферы» [3, с. 230]. Много позже, в 1903 году, в книге под многозначительным названием «Электричество и материя» автор более подробно рассказывает о проделанной им за 20 лет работе. В частности, после получения им математического выражения для массы он написал: «Это очень важный результат, так как он показывает, что часть массы заряженной сферы обязана своим происхождением ее заряду. Позже я предложу вам соображения, которые показывают возможность того, что вся масса тела имеет такое же происхождение» [10, с. 21].
Вот она теория «Великого Объединения» гравитационных и электромагнитных сил, о которой так долго твердили релятивисты! В теории относительности при отсутствии эфирной среды рост массы представляется чудом, которое вытекает из манипуляций формулами. Если томсоновская идея 1881 года еще не заслуживала называться полноценной теорией, то уж, во всяком случае, его подход к решению данной проблемы нужно признать абсолютно верным. Нет иного пути создания теории, объединяющей электромагнитные и гравитационные силы кроме моделирования на уровне общей для них мировой среды. Слепая манипуляция формулами здесь ни к чему не приведет.
В 1881 году Дж. Дж. Томсон вывел формулу массы m для сферы радиусом a, которая несет на себе заряд e: m = (4/15)e²/ac². Как видим, в данную формулу помимо указанных величин входит квадрат скорости света. Если это математическое выражение представить чуть-чуть иначе, а именно:
E = mc² = (4/15)e²/a,
то читатель легко узнает в ней знаменитую «эйнштейновскую» формулу, которой Дж. Дж. Томсон воспринимал настолько естественно, что не считал ее какой-то особенной. С самого начала он прекрасно осознавал, что коль скоро вся имеющаяся в природе масса имеет электромагнитное происхождение, то, разумеется, при определенных условиях некоторый объем вещества может переходить в электромагнитное излучение — это логическое следствие его понимания, как он тогда говорил, индуцированной массы. В цитируемой нами книге 1903 года он писал:
Следует отметить тот факт, что электростатическая энергия E в единице объема пропорциональна M — массе связанного эфира в этом объеме… E равно кинетической энергии, которой обладает связанная масса, движущаяся со скоростью света… Так как масса эфира, захватываемого фарадеевской трубкой, пропорциональна N, числу фарадеевских трубок в единице объема, то отсюда видно, что масса и количество движения фарадеевской трубки зависит не только от очертания и скорости рассматриваемой трубки, но и от числа и скорости соседних фарадеевских трубок [10, с. 33].В 1881 году Дж. Дж. Томсон еще не знал, как именно электромагнитная масса m зависит от скорости v перемещения сферы в неподвижном эфире, хотя и сделал кое-какие прикидки по увеличению массы Земли при ее движении на орбите вокруг Солнца. В первых расчетах у него получилась величина, равная 700 тыс. тонн, относительно которой он заметил: «масса совершенно незначительная по сравнению с массой Земли» [3, с. 234]. Он также еще не догадывался об изменении геометрии элементарного заряда и связанных с ним силовых трубок Фарадея. В 1889 году Оливер Хевисайд, заинтересовавшись работами Дж. Дж. Томсона написал статью, в которой показал, что фарадеевские трубки, равномерно распределенные по поверхности наэлектризованной сферы должны сдвигаться в определенном направлении. Известно, что опавший с дерева лист летит максимальной площадью по направлению падения, испытывая при этом максимальное сопротивление воздуха. При движении заряженной сферы фарадеевские трубки тоже располагаются таким образом, чтобы создать максимальное сопротивление движению. Это приводит к двум вещам: во-первых, к сокращению эффективных размеров связанной массы по направлению движения (впоследствии это сокращение назовут фицджеральдовским или лоренцевым) и, во-вторых, за счет увеличения сопротивления, — к росту массы движущейся сферы. В своей работе Хевисайд вывел также формулу, аналогичную формуле Дж. Дж. Томсона, только вместо коэффициента 4/15 он получил коэффициент 2/3.Процитируем фрагмент из книги «Электричество и материя», точнее, из параграфа под названием «Влияние скорости на связанную массу», где автор описывает данное явление с количественной точки зрения. «Было доказано (…) — здесь Дж. Дж. Томсон дает ссылку на работу Хевисайда, — что в результате движения сферы каждая фарадеевская трубка смещается по направлению к экваториальной плоскости, т.е. плоскости, проходящей через центр сферы и перпендикулярной к направлению движения. При этом смещение происходит таким образом, чтобы проекция трубки на эту плоскость оставалась такою же, как при равномерном распределении трубок, а расстояние каждой точки трубки от экваториальной уменьшилось в отношении (V² – v²)½ к V, где V — скорость распространения света, а v — скорость движения заряженного тела. Этот результат показывает, что только в том случае изменение и распределение фарадеевских трубок, вызванное движением тела, делается заметным, когда скорость движения заряженного тела сравнима со скоростью света.
В работе (…) я подсчитал количество движения J в пространстве, окружающем сферу радиуса a, центр которой находится на движущемся заряженном теле, и показал, что J дается следующим выражением:
» [10, с. 35].
Функцией F здесь обозначено громоздкое выражение, которое впоследствии утратило свое значение. Однако данная формула, в принципе, показывает верное изменение массы в зависимости от изменения относительной скорости β движущегося тела, которое в привычных обозначениях записывается как
.
Работы Дж. Дж. Томсона, О. Хевисайда и Г. Фицджеральда, проживавших в островной части Европы, горячо поддержали физики континентальной Европы. В 1897 году Л. Больцман, сориентированный на Англию больше других физиков, заметил в своих «Лекциях по принципам механики», что раньше физики стремились через механику объяснять все прочие явления, теперь было взято противоположное направление: через электромагнетизм нужно было попытаться объяснить механические понятия, каковыми является масса, инерция, сила, количество движения и энергия. В 1900 году В. Вин высказал аналогичное мнение, простирающиеся еще дальше: электромагнитные уравнения, писал он, должны стать основой для вывода уравнений механики. Для В. Кауфмана такое направление конструктивной мысли послужило толчком для проведения серии экспериментов, которые блестяще подтвердили правильность методологической установки, впервые сформулированной Дж. Дж. Томсоном. После получения Кауфманом эмпирического массива моделированием электронов и окружающей их мировой среды были заняты практически все известные физики-теоретики тогдашней Европы. В первых рядах стояли Г. Лоренц, М. Абрагам, А. Зоммерфельд, критиковавшие чужие формулы и предлагавшие свои для продольной и поперечной массы электрона, который отныне при своем движении увеличивал массу и терял сферическую форму, превращаясь в эллипсоид. Имея на руках числовые данные опыта можно было корректно судить, какие математические выражения и, соответственно, какая модель электрона и среды более точно отражает физическую реальность.
Таким образом, островная Европа, как в старые добрые времена опять стала диктовать правила высокого научного тона для континентальной Европы, которая еще не совсем освоилась с уравнениями Максвелла. Но вот всё тот же неутомимый исследователь, Дж. Дж. Томсон, столкнулся с волновыми свойствами электрона. Значит, решил он, электрон не является крохотной сферой с отходящими от нее фарадеевскими трубками; это несовместимо с волнами, распространяющимися в эфире. По-видимому, элементарный заряд представляет собой какой-то более мудрёный объект, чем думали о нем Фарадей, Максвелл и, после них, все остальные физики Европы. Вести о волновых свойствах электрона мгновенно распространились в ученом мире. Физики-экспериментаторы взялись за дело и поставили еще несколько любопытных опытов, в которых электрон вел себя то, как частица, то, как волна. Самым удивительным среди них был опыт, поставленный Артуром Комптоном в 1922 году. Он обнаружил, что частота рассеянных в веществе рентгеновских лучей иная, чем исходных лучей. Это довольно просто можно было объяснить, пользуясь корпускулярной моделью. Если представить рентгеновские лучи потоком фотонов, то их рассеяние на шарообразных электронах можно было описывать законами сохранения энергии и импульса, справедливыми для бильярдных шаров. Так до сих пор по уравнениям сохранения рассчитывается энергия электрона отдачи и так называемая комптоновская длина волны.
В целом физика на рубеже веков развивалась успешно. Возникали, конечно, на ее пути большие и малые трудности, в том числе и те, что указаны выше, но говорить о застое науки не приходилось. Однако в континентальной Европе медленно, но верно зрела реакция на передовые воззрения островной Европы. В среде влиятельных физиков Австрии, Германии, Голландии и Франции, склонных к формалистским и спекулятивным приемам анализа физических ситуаций всё больше и больше росло недовольство конструктивными методами англичан. В общем, борьба между формалистами и конструктивистами не прекращалась ни на день, лишь временами она слегка затухала, чтобы через какое-то время вспыхнуть с новой силой. Так, например, конструктивист Фарадей столкнулся с враждебными настроениями, идущими со стороны формалистов Ампера и Вебера. То, что магнитная стрелка отклоняется под действием электрического тока, Эрстед убедился еще в 1820 году. Физики Европы, естественно, предположили обратное: магнитное поле должно вызывать электрический ток. Однако многолетние усилия экспериментаторов ни к чему не привели. В 1825 году Ампер громогласно объявил, что искомой связи не существует и ставить эксперименты для ее обнаружения затея совершенно безнадежная.
Но Фарадей продолжал искать, пока, наконец, в 1831 году не открыл явление электромагнитной индукции. Академические ученые континентальной Европы откровенно презирали пространственно-механические конструкции, зарождавшиеся в голове нищего переплетчика и сторожа лаборатории, который к тому же абсолютно не разбирался в математике. Однако Максвелл увидел в этом скромном человеке гениального физика и решил все его идеи облечь в математическую форму. История науки не знает более успешного тандема двух ученых, которые встречались лишь однажды, причем о физике не сказали ни слова. И вот новая удача для мировой науки: в личности Дж. Дж. Томсона удивительным образом соединился талант дотошного экспериментатора Фарадея и скрупулезного теоретика Максвелла. Если бы формалисты еще при его жизни не пришли к власти и не подмяли под себя всех конструктивно думающих ученых, то он бы сейчас встал вровень с Архимедом, Коперником и Декартом.
В данной работе не ставится задача в полном объёме рассказать эпопею по взятию власти релятивистами. В общем, из истории науки известна гибельная роль философствующих физиков Маха и Пуанкаре, формалистские «перегибы», наблюдавшиеся в работах Лоренца и Минковского, которые, однако, к концу 1920-х годов уже сошли с арены мировой науки. Кроме того, как мы знаем, появились новые проблемы, требующие своего особого решения, и среди них проблема дуализма электрона стояла на первом месте. Нельзя сказать, что противоречивая ситуация с электроном в середине 1920-х годов была какой-то из ряда вон выходящей. Дж. Дж. Томсон, как мы знаем, уже стоял на пути ее разрешения. Но, как это часто бывает в переходные эпохи, формалистская группировка воспользовались моментом, объявила кризис конструктивной стратегии, наплодившей, как ей показалось, множество бесполезных моделей, и насильственными методами свергла власть конструктивистов.
В короткий исторический период между 1920 и 1930 годом судьбу науки решала небольшая генерация молодых физиков во главе с Нильсом Бором, Вернером Гейзенбергом и Максом Борном. Ошибочной эпистемологической позиции последнего посвящен большой раздел: Борн — тотальный релятивист. Там приведены фрагменты из пятой главы «Символ и реальность» книги Борна «Моя жизнь и взгляды». В 1954 году автору этой книги вручили Нобелевскую премию «за его фундаментальные работы по квантовой механике и, прежде всего, за статистическую интерпретацию волновой функции». Таким образом, к середине XX столетия с помощью чисто политического инструмента, каким всегда являлась Нобелевская премия, формалистам удалось окончательно закрепить победу над конструктивно мыслящими физиками, названными Борном «жалкими глупцами», ограничивающими свободу творчества.
Представлять электрон математической точкой — значит, бежать от физики в область умозрительной схоластики. Однако те, кто сегодня пользуется подобной техникой спекуляций, считается настоящим ученым, те же, кто апеллирует к чертежам и наглядным образам, ученым не считается (скорее, даже, наоборот, врагом науки, поскольку он подрывает устои). Вот почему не следует в скором будущем ожидать принятия правильной формулы Доплера: все вышеприведенные доказательства будут, скорее всего, проигнорированы официальной наукой. Они просто не будут восприняты современной корпорацией ученых, члены которой (a) за длительный период селекции отучились конструктивно думать пространственно-механическими категориями, и (б) не нуждаются в правильных формулах, та как вполне довольствуются договоренностями, установленными более века назад. Нужно не забывать, что Российская Академия (как, очевидно, и другие академии) — это своеобразная церковь. Истина может лишь подорвать установившуюся в ней власть и высокий социальный статус нынешних чиновников, которые в основном заняты дележом денег и чинов. Если даже кому-то из академических чиновников понравится точная формула (4) и он захочет поместить ее в официальный учебник, то академическая церковь тут же без большого шума придаст его анафеме и всё останется по-старому.
Эффект Дьявола
В свете вышеизложенного будет уместно познакомить нашего читателя не с эффектом божественной природы, а с эффектом Дьявола, который поселился в обществе людей и постоянно сбивает их с толку, не давая познать законы, установленные природой. С этой целью мы обратимся к докладу Лауреата НП, прочитанного в 1996 году по случаю присуждения ему Большой золотой медали. Выбранная им тема — «Излучение равномерно движущихся источников», т.е. об эффекте Вавилова – Черенкова — была особенно дорога его сердцу. Сама проблема подробно анализировалась выше, сейчас мы обратим внимание читателя на один эмоциональный штрих. «Люблю я проблематику, связанную с излучением равномерно движущихся источников, вероятно, потому, — поясняет Лауреат НП, что с ней связаны мои первые научные результаты, да и было это в молодости». Это — первая причина. «Вторая причина, обусловившая выбор темы доклада, — добавляет лауреат, — заключается в том, что излучение равномерно движущихся источников — это, буквально, российская и к тому же академическая тема» [2, с. 1033].
Лауреат НП использовал так называемый гамильтоновский метод, который «нагляден и технически прост. Характер настоящего доклада, — сказал по этому поводу Лауреат НП, — позволяет мне заметить здесь, что именно эта простота, с которой я случайно столкнулся, побудила меня заняться теоретической физикой (окончил же я МГУ в 1938 г. как оптик-экспериментатор и считал, что теоретиком мне становиться не следует в связи с недостаточными математическими способностями) [2, с. 1036]. Напомним, в своем докладе Лауреат НП доказывает, что «в вакууме равномерно движущийся заряд не излучает» [2, с. 1036], в среде же может иметь место излучение Вавилова – Черенкова, когда скорость движения заряда больше скорости распространения света в среде (β > 1). Для решения вопроса, почему излучения нет при β < 1, Лауреат НП создал специальную квантовую теорию, носящую теперь его имя, но которую трудно назвать научной. При ее создании он показал чрезвычайно низкую культуру научного мышления. Суждения его неаккуратны и, в принципе, ничего не доказывают. Причину такого исхода нужно искать в личности автора, к ознакомлению с которой мы тут же приступаем. Далее будет видно, что Лауреат НП и не мог создать математически строгую теорию.
*
* *В своем жизнеописании Гинзбург писал: «Меня родители (точнее, отец и тетя) послали почему-то только в 4-й класс, так что я учился в школе вообще лишь 4 года. Программы современной я не знаю, и, может быть, было и не так уж плохо. Но отсутствие соответствующей "учебной" атмосферы, и в семье в частности, в общем, оставило у меня впечатление, что получил я от школы мало» [6, 1138]. Об этом же, но уже чуть более подробно, Лауреат НП рассказывает в своей автобиографии, отосланной им в Нобелевский комитет, цитирую:
«…Меня послали в школу только в 11 лет (в 1927 г. я поступил в 4-й класс)… Это была бывшая французская гимназия… В 1931 г., как раз когда я окончил 7 классов, в СССР произошла очередная школьная реформа, и полная средняя школа была упразднена… После 7 классов полагалось поступать в фабрично-заводское училище (ФЗУ), где готовили, по идее, квалифицированных рабочих… [но] поступать в ФЗУ мне совсем не хотелось. Некоторое время оставался каким-то неприкаянным и несчастливым 15-летним мальчиком. … В 1931 г. … я устроился лаборантом в рентгеновской лаборатории технического ВУЗа…
То, что я приобрел в лаборатории, это не столько какие-то конкретные знания, сколько вкус к работе, к физике, изобретательству. Помню еще, что с интересом читал книгу О.Д. Хвольсона "Физика наших дней" — редкое тогда популярное сочинение о достижениях физики. Так или иначе, решил стать физиком, тем более, что никаких талантов у меня не было. К физике же был, по крайней мере, интерес.
Итак, решил поступать на физический факультет Московского госуниверситета (МГУ). А тут как раз с 1933 г. стало возможным поступать в МГУ по открытому конкурсу... Но для поступления в Университет нужно было пройти полный курс средней школы, а я ведь окончил лишь 7 классов [правильнее сказать, 4 класса, а не 7]. Вот и пришлось мне за месяца три овладеть (частично с учителем) знаниями, которые изучают в старших классах. Пишу об этом довольно подробно потому, что всю жизнь жалею о том, что не получил нормального среднего образования. И хочу предостеречь тех, кто думает, что на школьную премудрость не стоит тратить много лет. Действительно, хотя у меня, как я убежден, не более чем средние способности, я за три месяца "прошел" программу трех школьных лет. Но какой ценой? Цена, прежде всего, в отсутствии автоматизма в элементарной математике и орфографии даже русского языка. Конкретно, если бы в школе я решил, например, 100 каких-то задач по алгебре, тригонометрии и т.д., то сам решил их, скажем, лишь 10. Зачем решать много задач, если не требуют? А такое тянет за собой и отсутствие навыков при дальнейшем изучении математики. С орфографией то же самое… Не знаю я и языков, хотя, конечно, потом пришлось овладеть английским языком, да и то лишь в пределах, необходимых для занятий физикой…
На вступительных экзаменах на физфак МГУ в 1933 г. я ни на чем не провалился, но в целом сдал без блеска. В результате меня в университет не приняли… Поэтому я поступил на заочное отделение, что оказалось возможным. И опять меня ударило по больному месту. В 1934 г. мне удалось перевестись на очное отделение, на второй курс, т.е. я догнал своих товарищей и стал учиться, как все. Но узнал, насколько богаче и ярче была их жизнь при наличии всяких факультативных курсов и т.д. Я уже не говорю о том, что каким-то образом так и не познакомился с курсами астрономии и химии, которые не пришлось проходить заочно и как-то не был обязан "сдавать" при переходе на очное отделение…
Начиная со второго курса, я хорошо учился и, так сказать, с удовольствием. Мне нравилась теоретическая физика, но я считал и считаю, что способности к математике у меня в лучшем случае средние, а тут еще решал задачи и вычислял с трудом (см. выше). В то же время считалось и, в общем, справедливо, что физик-теоретик должен быть в ладах с математикой. Коротко говоря, в силу сказанного, когда в конце третьего курса или начале четвертого (уж теперь и не помню когда) нужно было выбрать специализацию, я не решился пойти в теоретики и выбрал оптическую специальность…
В общем, пользуясь так называемым гамильтоновским методом, я смог выяснить некоторые вопросы и решить ряд электродинамических задач как в вакууме, так и при движении зарядов в среде, например, задачу об излучении Вавилова – Черенкова при движении заряда в кристаллах. Никакой сложной математики мне при этом не понадобилось. Конечно, я обнаружил давно известное: как ни близки физика с математикой, их связь бывает самой различной и, в частности, можно успешно заниматься теоретической физикой, используя лишь весьма скромный математический аппарат, скажем, не выходящий за пределы излагаемого на физических факультетах. Другое дело, что в некоторых случаях физики-теоретики пользуются и самой сложной современной математикой, и развивают ее.
Итак, я понял, что могу работать, получать результаты, придумывать новые возможности. Все это доставляет большую радость, это счастье. И я много работал, сделал диссертацию… практически за год, а в 1940 г. ее защитил. Таким образом, я окончил аспирантуру на физфаке МГУ за два года вместо положенных трех; это там был, кажется, первый такой случай. Меня хотели оставить в Институте физики МГУ в каком-то качестве, но атмосфера там была плохая, и к великому счастью, с 1 сентября 1940 г. я стал докторантом ФИАНа… В аспирантуре моим руководителем числился Г. Ландсберг, поскольку предполагалось, что я буду заниматься оптикой. Но он благородно не мешал мне заниматься совсем другим. А в докторантуре моим куратором считался И. Тамм, тоже не мешавший заниматься, чем хочу. И в общем — это стиль, присущий физикам-теоретикам СССР и России, во всяком случае, во многих местах и, несомненно, в ФИАНе» [взято с ufn.ru].
Можно называть себя «физиком-теоретиком», добиться высокого карьерного роста, академического звания и даже Нобелевской медали, но, по сути, оставаться недоучкой, некомпетентным физиком. Лауреат НП блестяще продемонстрировал эту возможность. Подобное верхоглядство присуще многим релятивистам, иначе они не были бы приверженцами спекулятивного учения. Откровенное описание Гинзбургом своих математических «талантов» мало чем отличается от аналогичного описания, сделанного отцом-основателем релятивисткой догмы относительно своих математических способностей. Альберт Эйнштейн в своей автобиографии 1955 года сообщает:
... Высшая математика еще мало интересовала меня в студенческие годы. Мне ошибочно казалось, что это настолько разветвленная область, что можно легко растратить всю свою энергию в далекой провинции, к тому же по своей наивности я считал, что для физики достаточно твердо усвоить элементарные математические понятия и иметь их готовыми для применения, а остальное состоит в бесполезных для физики тонкостях, — заблуждение, которое только позднее я с сожалением осознал. У меня, очевидно, не хватало математических способностей, чтобы отличить центральное и фундаментальное от периферийного и не принципиально важного…
Я жаждал глубоких знаний, но обучение не казалось мне легкой задачей: я был мало приспособлен к заучиванию и обладал плохой памятью. С чувством вполне обоснованной неуверенности я явился на вступительный экзамен на инженерное отделение. Экзамен показал мне прискорбную недостаточность моей подготовки, несмотря на то, что экзаменаторы были снисходительны и полны сочувствия. Я понимал, что мой провал был вполне оправдан. 1896 — 1900 гг. — обучение на отделении преподавателей специальных дисциплин швейцарского политехникума. Вскоре я заметил, что довольствуюсь ролью посредственного студента. Для того чтобы быть хорошим студентом, нужно обладать легкостью восприятия; готовностью сконцентрировать свои силы на всем том, что читается на лекциях; любовью к порядку, чтобы записывать и затем добросовестно обрабатывать преподносимое на лекциях. Все этих качеств мне основательно недоставало, как я с сожалением установил. Так постепенно я научился ладить с не совсем чистой совестью и организовывать свое учение так, как это соответствовало моему интеллектуальному желудку и моим интересам. Некоторые лекции я слушал с большим интересом. Но обыкновенно я много "прогуливал"... [7, т. 4, с. 351].
Примерно то же самое он писал в «Автобиографических заметках» 1949 г., правда, куда менее откровенно.
Там [в Политехникуме], — пишет Эйнштейн, — у меня были прекрасные преподаватели (например, Гурвиц и Минковский), так что, собственно говоря, я мог бы получить солидное математическое образование. Я же большую часть времени работал в физической лаборатории, увлеченный непосредственным соприкосновением с опытом [7. т. 4, с. 264].Квалифицированный преподаватель математики, физики или просто знающий жизнь человек скажет вам, что ребенок, своевременно не получивший необходимых навыков по точным наукам, никогда в будущем не приобретет упущенных знаний. Его лексикон может стать богатым на различного рода научные словечки, он натренируется манипулировать формулами, но его мышление навсегда останется непоследовательным, склонным к необоснованным фантазиям и неспособным к выдвижению продуктивных идей. Эйнштейн, Гинзбург и бесчисленное множество других релятивистов усвоили два-три десятка схоластических терминов и примерно такое же количество алхимических формул, которыми они постоянно оперируют и ни за какие коврижки не откажутся от них, так как считают их священными. Выводить и понимать другие физико-математические выражения они не в состоянии.В результате деятельности этой огромной группы спекулянтов в мировом сообществе возник корпоративно-религиозный орден святого Эйнштейна. Первосвященники этой церкви всячески препятствуют всему тому, что может поколебать авторитет великого гуру. Влиятельные служители культа верховного божества окружают себя нисходящим каскадом жрецов — хранителей культа местных божков. У нас в России это Гинзбург, который начал исповедовать религию релятивизма еще до второй мировой войны. Все священные культы функционируют примерно по одним и тем же канонам, которые распространяются и на Гинзбурга.
Хочу напомнить, при выборе темы доклада 1996 года Гинзубург, как мы читали, назвал две причины, которые еще понять можно. Но позвольте спросить, какая причина заставила главного редактора журнала «Успехи физических наук» текст доклада, опубликованного в октябрьском номере за 1996 год, опубликовать его еще раз ровно через пять лет в октябре 2001 года [3]. И это притом, что на данную тему, начиная 1940 года, им уже было опубликована добрая дюжина статей.
Не ждите сенсаций, дорогой читатель, причина дублирования указанной статьи и нескольких других до боли знакома всякому россиянину и связана она с банальным культом личности главного редактора УФН. Редакционная коллегия в составе:
М.С. АКСЕНТЬЕВА (ответственный секретарь), B.C. БЕСКИН, В.Б. БРАГИНСКИЙ, Л.П. ГРИЩУК, Ю.В. ГУЛЯЕВ, И.М. ДРЕМИН (зам. главного редактора), Г.Р. ИВАНИЦКИЙ, А.А. КАПЛЯНСКИЙ, Г.Н. КУЛИПАНОВ, Л.Б. ОКУНЬ, Л.П. ПИТАЕВСКИЙ (зам. главного редактора), В.И. РИТУС, В.А. РУБАКОВ, О.В. РУДЕНКО, Б.М. СМИРНОВ (зам. главного редактора), В.Д. ШАФРАНОВиз неистребимого чувства раболепия решила преподнести бесценный подарок своему шефу и отпечатать его особо «гениальные» сочинения еще раз в журнале, который теперь впору назвать «Успехи Виталия Лазаревича». Эта форма подхалимства выглядит так глупо, что просто диву даешься. Ведь достаточно было привести ссылки на «нетленные» произведения Лауреата НП и каждый желающий мог бы зайти в Интернет на сайт ufn.ru, чтобы еще раз насладиться чтением «высоконаучных» текстов. Кстати, список трудов юбиляра в юбилейном номере приводится — этим надо было и ограничиться, но нет, нашим академикам обязательно нужно опозориться на весь мир.По-доброму, что могла бы сделать редакционная коллегия для своего горячо любимого руководителя. Если уж статьи Гинзбурга так хороши, пусть бы кто-нибудь из его угодников рассказал нам, темным людям, чем именно прекрасны его научные открытия, т.е. взял да прокомментировал их содержание и ткнул пальцем на особо яркие перлы гинзбургских идей. Вместо этого коллегия прислужников культа написала следующее велеречивое напоминание:
4 октября 2001 года исполняется 85 лет со дня рождения выдающегося физика-теоретика Виталия Лазаревича Гинзбурга.Вклад В.Л. Гинзбурга в науку и жизнь общества XX и XXI столетий исключительно велик. Он оценен высокими мировыми научными премиями, званиями и государственными наградами. Научные интересы В.Л. Гинзбурга охватывают многие разделы физики. Им были опубликованы фундаментальные работы по теории сверхпроводимости, сверхтекучести, сегнетоэлектричества, теории эффекта Вавилова – Черепкова и переходного излучения, радиоастрономии и происхождении космических лучей, проведены важные прикладные исследования.
Журнал "Успехи физических наук" по праву гордится тем, что Виталий Лазаревич как автор избрал именно журнал УФН для опубликования 99-ти статей по этим (и другим) разделам физики.
Поэтому, отмечая 85-летний юбилей Виталия Лазаревича, мы решили предложить вниманию читателей подборку опубликованных ранее в УФН, наиболее обобщающих статей В.Л. Гинзбурга по тем областям физики, в которых, по мнению самого В.Л. "... я сделал довольно много" (см. публикуемый в этом же номере очерк В.Л. Гинзбурга "Как я стал физиком-теоретиком и вообще о себе..", с. 1137). Волею случая новая — 100-я в УФН статья В.Л. Гинзбурга — также публикуется в этом дважды юбилейном номере (с. 1123).
Кроме того как главный редактор журнала УФН В.Л. выступил со многими интересными новациями в журнале. Так, по его инициативе появилась рубрика "Новости физики в сети Интернет", возродилась рубрика "Новые книги по физике и смежным наукам", была предложена рубрика "Трибуна УФН", помещенная первоначально только на сервере журнала УФН. В электронной версии этой рубрики были "для затравки" помещены статьи В.Л., касающиеся истории, филисофии, религии, жизни общества, — темам, которые наверняка будут небезынтересны читателям УФН. В этом номере мы впервые в печатной версии публикуем статьи в рубрике "Трибуна УФН", явившиеся откликом в Интернете на статью В.Л. Гинзбурга "Разум и вера" (также публикуемой в этом номере).
В этом юбилейном номере помещены исторические, биографические и библиографические статьи, связанные с именем В.Л. Гинзбурга.
Коллектив журнала УФН надеется, что данная юбилейная подборка с одной стороны будет интересна читателям, а с другой стороны рассматривает этот выпуск как дань уважения юбиляру и желает В.Л. Гинзбургу многих новых свершений!
*
* *Лауреат НП любит нашему глубоко православному народу лишний раз напомнить, что Бога нет. Мало ему телевизионной и газетной трибуны, ему нужно еще открыть трибуну в журнале «Успехи физических наук» и достижениями физики опровергать существование Высшей Личности. Как по заказу, именно в этом юбилейном номере, почти целиком посвященном чествованию почетного антиклерикала, была опубликовано сугубо клерикальная статья В.М. Липунова «Научно открываем Бога». Эта работа в 1995 году была напечатана в журнале «Земля и Вселенная» (No 1, 37), чуть позже, в журнале «Юность» и еще позже, в 2001 году, перепечатана в УФН. Романтика и наука! — Весьма характерное сочетание для нынешнего безвременья, поэтому хочу немного задержаться на этой статье.
В начале своего вдохновенно написанного текста автор обращается к шлягерам попсовой физики:
Я попытаюсь говорить о важнейшей проблеме современного естествознания, — проблеме, несомненно не менее важной, чем открытие черных дыр, создание теории великого объединения (ТВО) или создание искусственного интеллекта. Более того, на мой взгляд, она не только глубже и сложнее, но и несравненно актуальнее. Действительно: если под актуальностью понимать наличие некоего необъясненного явления, противоречащего существующим научным взглядам, то решение перечисленных выше сверхмодных (без всякой иронии) проблем в настоящий момент не обусловлено (и судя по всему, в обозримом будущем не будут вызваны) жесткой экспериментальной необходимостью. Сейчас, по крайней мере в физике (от физики низких температур до астрофизики), нет ни одного экспериментального факта, требующего создания теории великого объединения. Нет своего опыта, аналогичного опыту Майкельсона – Морли, потребовавшего нового представления о пространстве и времени. Такой эксперимент не скоро появится… [8, с. 1157].Анализируя содержание современных дао- и дзен-теорий, Липунов обременяет свой старческий разум непосильной проблемой поиска внеземного разума, модной в годы его юности. Но вот он написал с заглавных букв слова Внеземной Разум, и мы тотчас понимаем, какой астральный смысл он вкладывает в это прозаическое словосочетание, писавшееся в 1960-е годы, конечно же, с маленьких букв. Потом Липунов вспоминал Шкловского и Циолковского пока, наконец, не закончил Святым Эйнштейном, который в 1952 году написал рабу божьему Соловину:…Упорядочение, вносимое, например, ньютоновской теорией гравитации, носит совсем иной характер. Хотя аксиомы этой теории и созданы человеком, успех этого предприятия предполагает существенную упорядоченность объективного мира, ожидать которую априори у нас нет никаких оснований. В этом и состоит "чудо", и чем дальше развиваются наши знания, тем волшебнее оно становится. Позитивисты и профессиональные атеисты видят в этом уязвимое место, ибо они чувствуют себя счастливыми от сознания, что им не только удалось с успехом изгнать бога из этого мира, но и "лишить этот мир чудес". Любопытно, что мы должны довольствоваться признанием "чуда", ибо законных путей, чтобы выйти из положения, у нас нет. (Курсив мой. — В. Л.) Я должен это особенно подчеркнуть, чтобы Вы не подумали, будто я, ослабев к старости, стал жертвой попов».Типичное для верующих онтологическое доказательство присутствия в нашем мире Высшего Существа. Во все времена теологи нам говорили: «Ну, посмотрите вокруг, как всё великолепно устроено! Разве это восхитительное мироздание могло возникнуть без вмешательства Магической Силы?» Аргументация Блаженного Альберта до тошноты банальна, но Липунову она приглянулась. Особенно поразило его возбудимое воображение две вещи:Первое — признание существования настоящего "Космического Чуда", и второе — несомненное понимание того, что из этого немедленно должно последовать признание существования Бога, но сделать это, конечно, нельзя, чтобы не стать "жертвой попов". Но и нельзя одновременно признать бесконечную сложность мира и успешную его познаваемость (т.е. фактически само существование разума в бесконечно сложном мире) и не признать при этом существование Сверхразума — научно открываемого Бога [8, с. 1160].Есть! Липунову удалось поймать Бога за бороду. Дальше разум его помутнел и посиневшими губами он пробормотал:Что есть научно открываемый Бог, или Сверхразум, и что есть будущая наука о бесконечно сложном Мире? Может ли вообще человеческий разум создать хотя бы примитивную модель, теорию, концепцию бесконечно сложного, непознаваемого по частям объекта? В рамках современной науки — вряд ли… Сам математический аппарат, с которым имеет дело современная физика, основан изначально на цифровом пастушьем опыте чисел — стадо баранов может быть расчленено на отдельные особи и посчитано. (Приходится только опять удивиться, как при этом мелком багаже науке удалось проникнуть в глубинные тайны Вселенной и атомов?) В нем, классическом научном методе, изначально заложен прогрессистский подход от простого к сложному. В этом и состоит смысл современной науки — "объяснить". Но в человеческом лексиконе есть еще два важных слова — "понять" и "поверить". Одно из них принадлежит, скорее, искусству, и особенно литературе (она, как и наука, использует язык слов), а другое — религии. Но как совместить это все вместе, каким образом можно придать, например, формальным математическим высказываниям этическую окраску? И как наш научно открываемый Бог, к которому неизбежно пришла современная простая наука, соотносится с Богом религиозным?Приехали… Можно подумать, что мы читаем не серьезный научный журнал «Успехи физических наук», а какой-то легковесный ЖЖ-текст, написанный 16-летним подростком, потерявшимся в нашем сложном и противоречивом мире. На своем сайте (pereplet.ru) Владимир Михайлович стал оправдываться: «Я ни в коем случае не имел в виду Бога религиозного». Полно заливать! Непредвзято мыслящий читатель понимает, что атеист не озаглавил бы свои выступления: «Физические явления на небесах»? У автора настолько романтическое сознание, что лучше бы ему заниматься только писательским трудом (Липунов — член Союза писателей) и оставить науку. Но он — на беду российской науки — еще и профессор кафедры астрофизики и звездной астрономии МГУ. Когда литератор и астроном совмещаются в одном лице, получается искатель Внеземного Разума и Потусторонних Миров (Липунов обнаружил несколько чёрных дыр).Один верующий на мой вопрос о том, как Ветхий Завет сочетается с современной оценкой возраста Вселенной в десять миллиардов лет, ответил: "Десять тысяч лет назад в течение одной рабочей недели Господь Бог создал мир, которому было десять миллиардов лет". Это звучит не только остроумно…
По-видимому, двигаться дальше можно, лишь пытаясь отвечать на необычные вопросы. Например, как соотносятся понятия добра и зла с принципом причинности? А с присутствием времени или его отсутствием? Возможны ли подтексты в научных высказываниях, двусмысленности, вероятностная интерпретация?
Одним из важнейших естественнонаучных направлений, конечно, должен быть поиск Внеземного Разума [читай: Бога]. При этом нужно трезво понимать, что сам факт открытия обитаемых планетных систем хоть и интересен, но вряд ли приведет к существенному продвижению. Такое открытие сродни открытию индейцев Колумбом. Гораздо важнее не они сами как биологический вид, а их представление о Боге, о Добре и Зле.
*
* *Недавно, просматривая УФН эпохи Гинзбурга, наткнулся на смешное извинение. Оно короткое, процитирую полностью:
В августе 2004 года в УФН (т. 175, № 8, с. 899) была опубликована статья Д.Е. Бурланкова "Тяготение и абсолютное пространство. Работы Нильса Бьёрна (1865-1909)".Интересное историческое описание встречи Нильса Бьёрна с выдающимся норвежским математиком Софусом Ли и научной дискуссии между ними послужило основой решения о публикации этой статьи. После публикации статьи редакция передала ее в посольство Норвегии в России с просьбой прислать биографические сведения о Бьёрне и упомянутой в статье его внучке Анне Флоренс. В ответе от посольства и университета Осло сообщалось, что ни в каких официальных документах ни Бьёрн, ни Флоренс не числятся. Позднее Д.Е. Бурланков в своем письме в редакцию извинился и признался в том, что Нильс Бьёрн — персонаж вымышленный, а дискуссия между ним и Софусом Ли использована лишь как способ наглядной демонстрации точки зрения автора ("мысленный эксперимент" согласно Бурланкову) на общую теорию относительности.
В литературе широко используется художественный прием, основанный на встречах и беседах вымышленных персонажей или реальных людей, живших в разные эпохи. Однако УФН — это научный журнал, и точность как научных, так и исторических фактов здесь абсолютно необходима. Во всяком случае, такие методы подачи материала требуют специального обсуждения и недвусмысленных оговорок в тексте.
Редколлегия приносит извинения читателям за публикацию статьи Д.Е. Бурланкова.
Правда, смешно? Это извинение редакция УФН назвала «Уведомление читателям» (правильнее писать «Уведомление читателей»), которое можно понять и так: «Дорогие читатели, мы не обладаем требуемой для редакторской работы квалификацией и не можем отличить правду от вымысла. Поэтому нижайше просим вас, больше не обманывать нас, простаков; присылайте, пожалуйста, тексты о событиях реальных, а не придуманных».
*
* *Эффект Дьявола – это социально-психологическое явление, связанное с переходом божественной личности в свою противоположность — личность дьявольскую. Данный эффект особенно часто дает о себе знать в сфере науки. Например, некогда авторитетный ученый, удостоившийся всяческих почестей, более не слышит колокольчика, который настойчиво звенит ему: «Динь-динь, уходи, твое время вышло». Но он окружил себе толпой лицемеров-паразитов, которые в один голос кричат: «Ты наше национальное достояние. Не уходи, еще не родился на земле человек, который мог бы тягаться с Тобою быстротою и прозорливостью ума. Ты — наш сегодняшний Эйнштейн, ученье которого переживет тысячелетия».
«Божественная личность», обманутая такой лестью, естественно, забывает, что жизнь не стоит на месте, а тем более наука. То, чему учил сто лет назад Моисей-Эйнштейн, сегодня умерло. Его спекуляции, которые, быть может, еще в конце прошлого века выглядели свежо и оригинально, в начале нынешнего сильно выцвели, покрылись слоем пыли и затянулись паутиной. «Наше национальное достояние» продолжает исповедовать старую догму. Властные институты Большого Зла, созданные под дряхлеющее «Божество», продолжают внушать несведущим: «Посмотрите, как молод душой этот Старец, как смелы и мудры его думы, как лихо Он ставит на место своих идейных противников. Разве это не свидетельствует, что наш Бог еще молод душой? Так пусть же Он продолжает указывать нам, сирым и убогим, светлый путь в Мире Непознанного».
В это самое время «Бог» превращается в сущего Дьявола. Он поселяется в Академии наук и вещает оттуда: «Кто усомнится в истинности академической науки, тот — не ученый, тому нет места в Славном Храме Науки». Он также создает специальную «Комиссию по борьбе с лженаукой». При этом всем говорит: «Лженаукой называется любое учение, противоречащее божественному учению Святой Академии». Отныне созданная Дьяволом Святая Инквизиция карает всякого, кто посмеет усомниться в святости Антибога и учения, которое тот пестовал всю свою долгую жизнь. Члены комиссии на сто процентов уверены, что всё верное — неново, а всё новое — неверно. Они реально думает, что здравая научная мысль не может зародиться в «неакадемических» головах населения.
[1] Франк И.М. Излучение Вавилова – Черенкова. Вопросы теории. – М.: Наука, 1988.
[2] Гинзбург В.Л. Излучение равномерно движущихся источников (эффект Вавилова – Черенкова, переходное излучение и некоторые другие явления). УФН 166 1033 (1996).
[3] Гинзбург В.Л. Излучение равномерно движущихся источников (эффект Вавилова – Черенкова, переходное излучение и некоторые другие явления). УФН 171 109 (2001).
[4] Гинзбург В.Л. Некоторые вопросы теории излучения при сверхсветовом движении в среде. УФН LXIX 537 (1959).
[5] Скобельцын Д.В. Парадоксы квантовой теории эффектов Вавилова – Черенкова и Доплера. УФН 122 295 (1977).
[6] Гинзбург В.Л. Как я стал физиком-теоретиком и вообще о себе... УФН 171 1138 (2001).
[7] Эйнштейн А. Собрание научных трудов в 4-х. — М., 1965.
[8] Липунов В.М. Научно открываем Бога. УФН 171 1155 (2001).
[9] Томсон Дж. Дж. За пределами электрона. УФН VIII 570 (1928).
[10] Томсон Дж. Дж. Электричество и материя. – М. – Л.: Государственное издательство, 1928.




